বৃত্তের ক্ষেত্রফল ক্লাস 9 অধ্যায় 18 এর সমস্ত নিজে করি অঙ্ক একত্রে || Nije Kori of Chapter 18 Class 9 Area of Circle –এখানে নবম শ্রেণীর গণিত প্রকাশ বইয়ের বৃত্তের ক্ষেত্রফল অধ্যায়ের (অধ্যায়-18) সমস্ত ‘নিজে করি’ অঙ্কের সমাধান খুব সহজ পদ্ধতিতে করে দেওয়া হল । প্রয়োগ-3 , প্রয়োগ-5 ,প্রয়োগ-9 ,প্রয়োগ-11 , প্রয়োগ-24 , প্রয়োগ-27 , প্রয়োগ-30 এর (i) ও (ii) এর অঙ্কগুলো তোমাদের সমাধান করতে সমস্যা হলে এখান থেকে সাহায্য নিতে পারো । আর ক্লাস 9 এর ফাইনাল পরীক্ষার জন্য এই অঙ্কগুলিকে এখনই প্র্যাকটিস করে নাও ।
বৃত্তের ক্ষেত্রফল ক্লাস 9 অধ্যায় 18 এর সমস্ত নিজে করি অঙ্ক একত্রে || Nije Kori of Chapter 18 Class 9 Area of Circle
প্রয়োগ-3. যে বৃত্তের ব্যাসের দৈর্ঘ্য 42 সেমি. তার ক্ষেত্রফল হিসাব করে লিখি ।
সমাধানঃ বৃত্তের ব্যাসের দৈর্ঘ্য 42 সেমি.
∴ বৃত্তের ব্যাসার্ধ (r) =$\frac{42}{2}$ সেমি. =21 সেমি.
∴ বৃত্তের ক্ষেত্রফল
=$\pi r^2$
= $\frac{22}{7} \times 21^2 $ বর্গ সেমি.
=$ \frac{22}{7} \times 21 \times 21$ বর্গ সেমি.
= $\frac{22}{7} \times 21^3 \times 21$ বর্গ সেমি.
= $66 \times 21$ বর্গ সেমি.
= 1386 বর্গ সেমি.
উত্তরঃ বৃত্তের ক্ষেত্রফল 1386 বর্গ সেমি. ।
প্রয়োগ-5 যে বৃত্তের ক্ষেত্রফল 1 বর্গ মিটার 54 বর্গ ডেসিমিটার , তার ব্যাসার্ধের দৈর্ঘ্য হিসাব করে লিখি ।
সমাধানঃ বৃত্তের ক্ষেত্রফল 1 বর্গ মিটার 54 বর্গ ডেসিমিটার = (100+54) বর্গ ডেসিমিটার =154 বর্গ ডেসিমিটার।
ধরি , বৃত্তের ব্যাসার্ধ r ডেসিমিটার ।
∴ $\pi r^2 = 154$
$\Rightarrow \frac{22}{7} \times r^2 = 154$
$\Rightarrow r^2 = \frac{154 \times 7}{22}$
$\Rightarrow r^2 = 49$
$\Rightarrow r^2 = 7^2$
$\Rightarrow r = 7$
∴ বৃত্তের ব্যসার্ধ 7 ডেসিমিটার ।
প্রয়োগ-9: যদি লোহার বলয়ের ভিতরের ও বাহিরের ব্যাসের দৈর্ঘ্য যথাক্রমে 70 সেমি. ও 42 সেমি. হতো , তাহলে বলয়টিতে কত বর্গ সেমি. লোহার পাত থাকত হসাব করে লিখি ।
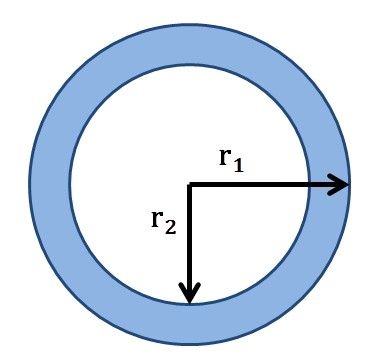
সমাধানঃ লোহার বলয়ের বাহিরের ব্যাসার্ধ (r2) =$\frac{70}{2}$ সেমি. =35 সেমি এবং লোহার বলয়ের ভিতরের ব্যাসার্ধ (r1) = $\frac{42}{2}$ =21 সেমি.।
বলয়টিতে যে পরিমাণ লোহার পাত থাকবে তা হল বলয়ের ক্ষেত্রফল ।
∴ বলয়টির ক্ষেত্রফল
= $\pi \left(r_2\right)^2 – \pi \left(r_1\right)^2$ বর্গ সেমি.
= $\pi \left\{\left(r_2\right)^2 – \left(r_1\right)^2\right\}$ বর্গ সেমি.
= $\frac{22}{7} \times \left\{(35)^2 – \left(21\right)^2\right\}$ বর্গ সেমি.
= $\frac{22}{7} \times (35 + 21)(35 – 21)$ বর্গ সেমি.
= $\frac{22}{7} \times 56 \times 14$ বর্গ সেমি.
= $22 \times 56 \times 2$ বর্গ সেমি.
= 2464 বর্গ সেমি.
উত্তরঃ বলয়টিতে পাত থাকবে 2464 বর্গ সেমি. ।
প্রয়োগ-11 : যদি বৃত্তাকার মাঠে সমান চওড়া রাস্তাটির বাইরের সীমারেখার দৈর্ঘ্য ভিতরের সীমারেখার দৈর্ঘ্যের থেকে 220 মিটার বেশি হতো এবং পথটির ক্ষেত্রফল 19250 বর্গ মিটার হতো , তাহলে বৃত্তাকার মাঠের ক্ষেত্রফল কত হতো হিসাব করে লিখি ।
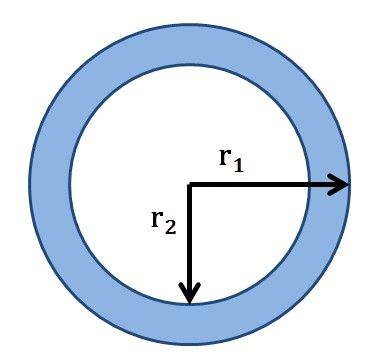
সমাধানঃ ধরি, রাস্তাসহ বৃত্তাকার মাঠের ব্যাসার্ধের দৈর্ঘ্য r2 মিটার এবং রাস্তা বাদে বৃত্তাকার মাঠের ব্যাসার্ধের দৈর্ঘ্য r1 মিটার ।
শর্তানুসারে,
$2{\mathrm{\pi}}{\mathrm{r}}_2 – 2{\mathrm{\pi}}{\mathrm{r}}_1 = 220$
$\Rightarrow 2{\mathrm{\pi}}\left({\mathrm{r}}_2 – {\mathrm{r}}_1\right) = 220$
$\Rightarrow 2 \times \frac{22}{7} \times \left({\mathrm{r}}_2 – {\mathrm{r}}_1\right) = 220$
$\Rightarrow {\mathrm{r}}_2 – {\mathrm{r}}_1 = \frac{220 \times 7}{2 \times 22}$
$\Rightarrow {\mathrm{r}}_2 – {\mathrm{r}}_1 = 35$ —-(i)
${\mathrm{\pi}}{\mathrm{r}}_2^2 – {\mathrm{\pi}}{\mathrm{r}}_1^2 = 19250$
$\Rightarrow {\mathrm{\pi}}\left({\mathrm{r}}_2^2 – {\mathrm{r}}_1^2\right) = 19250$
$\Rightarrow \frac{22}{7} \times \left({\mathrm{r}}_2 + {\mathrm{r}}_1\right)\left({\mathrm{r}}_2 – {\mathrm{r}}_1\right) = 19250$
$\Rightarrow \left({\mathrm{r}}_2 + {\mathrm{r}}_1\right)\left({\mathrm{r}}_2 – {\mathrm{r}}_1\right) = \frac{19250 \times 7}{22}$
$\Rightarrow \left({\mathrm{r}}_2 + {\mathrm{r}}_1\right)\left({\mathrm{r}}_2 – {\mathrm{r}}_1\right) = 875 \times 7$
$\Rightarrow \left({\mathrm{r}}_2 + {\mathrm{r}}_1\right) \times 35 = 875 \times 7$ [যেহেতু , r2-r1=35]
$\Rightarrow \left({\mathrm{r}}_2 + {\mathrm{r}}_1\right) = \frac{875 \times 7}{35}$
$\Rightarrow \left({\mathrm{r}}_2 + {\mathrm{r}}_1\right) = 25 \times 7$
$\Rightarrow \left({\mathrm{r}}_2 + {\mathrm{r}}_1\right) = 175$ —-(ii)
(i) এবং (ii) নং সমীকরণ যোগ করে পাই ,
r2+r1 + r2 – r1 = 175 +35
2r2= 210
r2 = $\frac{210}{2}$
r2 = 105
(i) নং সমীকরণে 105 বসিয়ে পাই ,
r2-r1= 35
∴ 105-r1=35
⟹ r1= 105-35
⟹ r1= 70
∴ বৃত্তাকার মাঠের ক্ষেত্রফল
$\frac{22}{7} \times (70)^2$ বর্গ মিটার
= $\frac{22}{7} \times 70 \times 70$ বর্গ মিটার
= $700 \times 22$ বর্গ মিটার
= 15400 বর্গ মিটার
বৃত্তের ক্ষেত্রফল ক্লাস 9 অধ্যায় 18 এর সমস্ত নিজে করি অঙ্ক একত্রে || Nije Kori of Chapter 18 Class 9 Area of Circle
প্রয়োগ-24: একটি অর্ধবৃত্তাকার পার্কের পরিসীমা 108 মিটার হলে তাহলে পার্ক টির ক্ষেত্রফল কত হবে হিসাব করে লিখি ।
সমাধানঃ ধরি , অর্ধবৃত্তাকার পার্কটির ব্যাসার্ধ r মিটার ।
∴ অর্ধবৃত্তাকার পার্কের পরিসীমা = ${\mathrm{\pi}}{\mathrm{r}} + 2{\mathrm{r}}$ মিটার
শর্তানুসারে ,
${\mathrm{\pi}}{\mathrm{r}} + 2{\mathrm{r}} = 108$
$\Rightarrow {\mathrm{r}}({\mathrm{\pi}} + 2) = 108$
$\Rightarrow {\mathrm{r}}\left(\frac{22}{7} + 2\right) = 108$
$\Rightarrow {\mathrm{r}} \times \frac{36}{7} = 108$
$\Rightarrow {\mathrm{r}} = \frac{108 \times 7}{36}$
$\Rightarrow {\mathrm{r}} = 21$
$\therefore$ বৃত্তের ক্ষেত্রফল
= $\frac{{\mathrm{\pi}}{\mathrm{r}}^2}{2}$ বর্গ মিটার
= $\frac{1}{2} \times \frac{22}{7} \times \left(21\right)^2 $ বর্গ মিটার
= $\frac{11}{7} \times 21 \times 21$ বর্গ মিটার
= $11 \times 3 \times 21$ বর্গ মিটার
= $33 \times 21$ বর্গ মিটার
= 693 বর্গ মিটার
প্রয়োগ 27: আমি নীচের চিত্রের রঙিন জায়গার ক্ষেত্রফল হিসাব করে লিখি ।
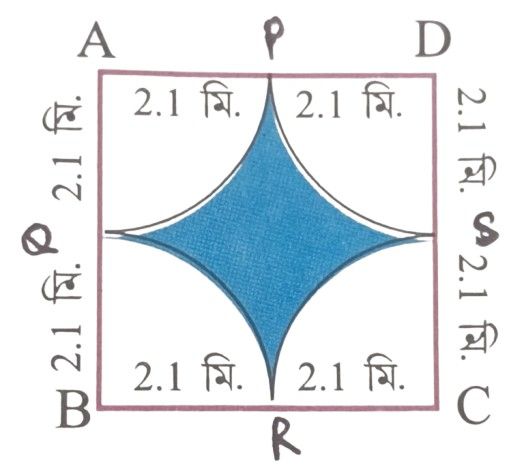
সমাধানঃ স্পষ্টতই ABCD চতুর্ভুজটি একটি বর্গক্ষেত্র ।
∴ বর্গক্ষেত্রটির প্রতিটি বাহুর দৈর্ঘ্য (2.1+2.1) মিটার = 4.2 মিটার ।
∴ ABCD বর্গক্ষেত্রের ক্ষেত্রফল
= (4.2)2 বর্গ মিটার
= 17.64 বর্গ মিটার
এখন , APQ বৃত্তকলার ক্ষেত্রফল
= $\frac{90}{360} \times {\mathrm{\pi}}{\mathrm{r}}^2 $ বর্গ মিটার
= $\frac{1}{4} \times \frac{22}{7} \times \left(2.1\right)^2 $ বর্গ মিটার
= $\frac{1}{4} \times \frac{22}{7} \times 2.1 \times 2.1$ বর্গ মিটার
= $\frac{1}{4} \times 22 \times 0.3 \times 2.1$ বর্গ মিটার
= $\frac{13.86}{4}$ বর্গ মিটার
∴ চারটি বৃত্তকলার ক্ষেত্রফল
= $4 \times \frac{13.86}{4}$ বর্গ মিটার
= 13.86 বর্গ মিটার
সুতরাং , রঙিন অংশের ক্ষেত্রফল
= (17.64 – 13.86 ) বর্গ মিটার
= 3.78 বর্গ মিটার
উত্তরঃ রঙিন অংশের ক্ষেত্রফল 3.78 বর্গ মিটার ।
প্রয়োগ-30: আমি নীচের বৃত্তকলাগুলির নকশার জায়গার (Shaded Area) পরিসীমা ও ক্ষেত্রফল হিসাব করে লিখি ।
(i)
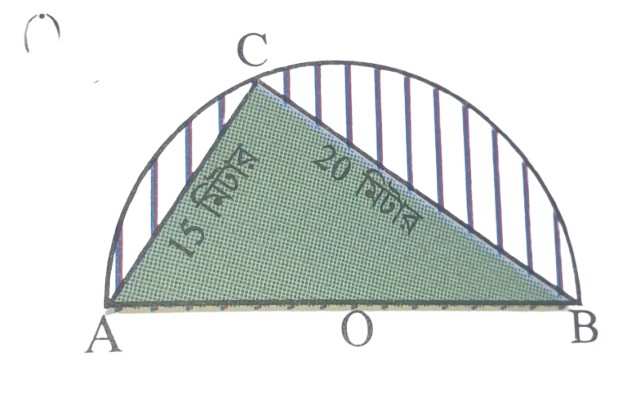
সমাধানঃ
যেহেতু AB হল অর্ধবৃত্তটির ব্যাস ,
∴ ACB একটি সমকোণী ত্রিভুজ যার কোণ ACB সমকোণ । কারণ , অর্ধবৃত্তস্থ কোণ সমকোণ ।
এখন , ACB সমকোণী ত্রিভুজের ক্ষেত্রে পিথাগোরাসের সূত্র প্রয়োগ করে পাই ,
AC2+BC2 = AB2
∴ (15)2 + (20)2 = AB2
বা, AB2 = 225 + 400
বা, AB2= 625
বা, AB2 =252
বা, AB = 25
অর্ধবৃত্তটির ব্যাসের দৈর্ঘ্য 25 মিটার ।
∴ ব্যাসার্ধ =$\frac{25}{2}$ মিটার
∴ অর্ধবৃত্তটির ক্ষেত্রফল
= $\frac{1}{2} \times {\mathrm{\pi}} \times \left(\frac{25}{2}\right)^2$ বর্গ মিটার
=$ \frac{1}{2} \times \frac{22}{7} \times \frac{25}{2} \times \frac{25}{2}$ বর্গ মিটার
= $\frac{11 \times 625}{28}$ বর্গ মিটার
= 245.53 বর্গ মিটার
ত্রিভুজ ACB এর ক্ষেত্রফল
= $\frac{1}{2} \times 15 \times 20$ বর্গ মিটার
= 150 মিটার
∴ নকশার জায়গার ক্ষেত্রফল
= (245.53 – 150 ) বর্গ মিটার
= 95.54 বর্গ মিটার (প্রায়)
আবার নকশার জায়গার পরিসীমা
= $\left(\frac{22}{7} \times \frac{25}{2} + 15 + 20\right)$ মিটার
= $\frac{11 \times 25}{7} + 35$ মিটার
= $\frac{275}{7} + 35$ মিটার
= 39.285 + 35 মিটার
= 74.29 মিটার (প্রায়)
(ii)
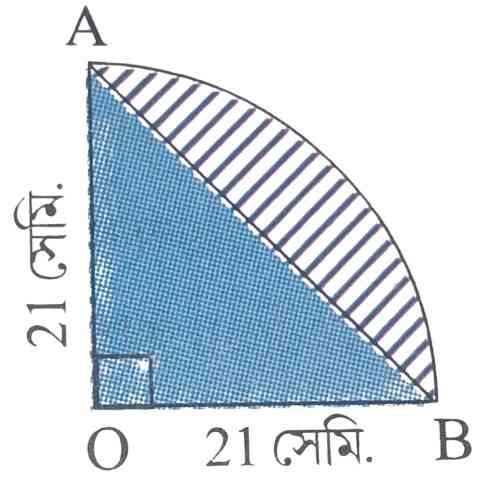
সমকোণী ত্রিভুজ AOB এর ক্ষেত্রফল
= $\frac{1}{2} \times 21 \times 21$ বর্গ সেমি.
= $\frac{441}{2}$ বর্গ সেমি.
আবার AOB বৃত্তকলার ক্ষেত্রফল
= $\frac{1}{4} \times {\mathrm{\pi}} \times (21)^2$ বর্গ সেমি.
= $\frac{1}{4} \times \frac{22}{7} \times 441$ বর্গ সেমি.
= $\frac{1}{4} \times 22 \times 63$ বর্গ সেমি.
=$ \frac{11 \times 63}{2}$ বর্গ সেমি.
= $\frac{693}{2}$ বর্গ সেমি.
∴ রেখাঙ্কিত অঞ্চলের ক্ষেত্রফল
= $\left(\frac{693}{2} – \frac{441}{2}\right)$ বর্গ সেমি.
= $\frac{252}{2}$ বর্গ সেমি.
= 126 বর্গ সেমি.
রেখাঙ্কিত অঞ্চলের পরিসীমা
=অতিভুজ AB + বৃত্তচাপ AB
=$ \sqrt{21^2 + 21^2} + \frac{2 \times {\mathrm{\pi}} \times 21}{4}$ সেমি.
= $\sqrt{441 + 441} + \frac{44}{7} \times \frac{21}{4}$ সেমি.
=$ \sqrt{882} + 33 $ সেমি.
= $\sqrt{2 \times 441} + 33$ সেমি.
= $21\sqrt{2}$ + 33 সেমি.
= 29.694 + 33 সেমি.
= 62.694 সেমি.
= 62.69 সেমি.
Important Links
আমাদের এই POST টি, আপনাদের পছন্দ হলে Share করার অনুরোধ রইল । এইরকম আরও সুন্দর সুন্দর POST পাওয়ার জন্য আমাদের FACEBOOK PAGE টি LIKE করুন ,WhatsApp চ্যানেল জয়েন করুন এবং YouTube Channel Subscribe করুন ।