সদৃশতা কষে দেখি ১৮.৪|Koshe Dekhi 18.4 Class 10|মাধ্যমিক গণিত প্রকাশ দশম শ্রেণি (ক্লাস ১০)(টেন) কষে দেখি 18.4|Madhyamik Math Solution Of Chapter 18 Similarity|Ganit Prakash Class 10 Koshe Dekhi 18.4 |মাধ্যমিক গণিত প্রকাশ ক্লাস ১০ সদৃশতা সমাধান|Madhyamik Math Solution In Bengali.
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
সদৃশতা কষে দেখি ১৮.৪|Koshe Dekhi 18.4 Class 10|কষে দেখি 18.4 ক্লাস 10
1. ∆ABC ত্রিভুজের ABC = 90° এবং BD লম্ব AC; যদি BD=8সেমি. এবং AD=5 সেমি. হয়, তবে CD-এর দৈর্ঘ্য হিসাব করে লিখি ।
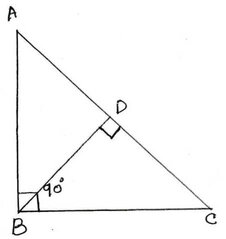
সমাধানঃ ∆ABC ত্রিভুজের ∠ABC = 90° এবং সমকৌণিক বিন্দু B থেকে অতিভুজ AC এর উপর BD লম্ব । যেহেতু সমকোণী ত্রিভুজের সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে লম্বের উভয়পার্শ্বে যে দুটি ত্রিভুজ উৎপন্ন হয় তারা পরস্পর সদৃশ ।
∴ ∆BDC এবং ∆ADB সদৃশকোণী।যেহেতু, সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতী,
বা, 5CD = 64
বা, CD = 64/5
বা, CD = 12.8
∴ CD এর দৈর্ঘ্য 12.8 সেমি. ।
সদৃশতা কষে দেখি ১৮.৪|Koshe Dekhi 18.4
2.∆ABC একটি সমকোণী ত্রিভুজ যার B সমকোণ এবং BD লম্ব AC ; যদি AD=4সেমি. এবং CD=16 সেমি. হয়, তবে BD ও AB এর দৈর্ঘ্য হিসাব করে লিখি ।
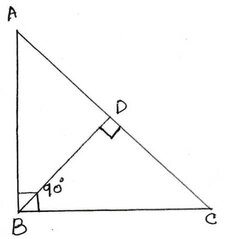
সমাধানঃ ∆ABC ত্রিভুজের ABC = 90° এবং সমকৌণিক বিন্দু B থেকে অতিভুজের উপর AC লম্ব ।যেহেতু সমকোণী ত্রিভুজের সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে লম্বের উভয়পার্শ্বে যে দুটি ত্রিভুজ উৎপন্ন হয় তারা পরস্পর সদৃশ ।
∴ ∆BDC এবং ∆ADB সদৃশকোণী।যেহেতু, সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতী,
বা, BD2 = 64
বা, BD = √64
বা, BD = 8
এখন সমকোণী ত্রিভুজ ∆ADB তে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই ,
AB2=AD2+BD2
বা, AB2= (4)2+(8)2
বা, AB2=16+64
বা, AB2 = 80
বা, AB = √80
বা, AB = √(5✕4✕4)
বা, AB = 4√5
∴ BD = 8 সেমি. এবং AB= 4√5সেমি.।
সদৃশতা কষে দেখি ১৮.৪|Koshe Dekhi 18.4
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
3. O কেন্দ্রীয় বৃত্তের AB একটি ব্যাস । P বৃত্তের উপর যেকোনো একটি বিন্দু । A ও B বিন্দুতে অঙ্কিত স্পর্শক দুটিকে P বিন্দুতে অঙ্কিত স্পর্শকটি যথাক্রমে Q ও R বিন্দুতে ছেদ করেছে । যদি বৃত্তের ব্যাসার্ধ r হয় , প্রমাণ করি যে, PQ.PR=r2
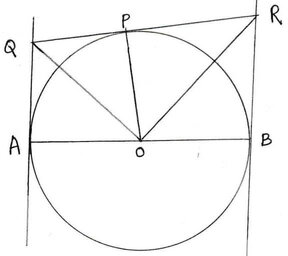
সমাধানঃ O কেন্দ্রীয় বৃত্তের AB ব্যাস । A ও B বিন্দুতে অঙ্কিত স্পর্শকদ্বয় P বিন্দুতে অঙ্কিত স্পর্শক Q এবং R বিন্দুতে ছেদ করেছে । বৃত্তের ব্যাসার্ধ r একক ।প্রমাণ করতে হবে যে PQ.PR = r2 .
অঙ্কনঃ O,P;O,Q এবং O,R যুক্ত করা হল ।
প্রমাণঃ P বিন্দুতে QR স্পর্শক এবং OP স্পর্শ বিন্দুগামী ব্যাসার্ধ ।
∴ OP ⊥ QR
আবার , OA স্পর্শ বিন্দুগামী ব্যাসার্ধ এবং AQ স্পর্শক ∴ OAQ = 90°
এখন ∆AOQ এবং ∆POQ ত্রিভুজের ক্ষেত্রে ,
∠OAQ = ∠OPQ [ উভয়ই 90° ]
OQ সাধারণ বাহু
যেহেতু ,বহিঃস্থ বিন্দু Q থেকে দুটি স্পর্শক AQ এবং PQ অঙ্কন করা হয়েছে,সুতরাং তারা সমান
∴ AQ = PQ
∴ ∆AOQ ≅ ∆POQ
∴ ∠AOQ = ∠POQ
অনুরূপে পাই , ∆BOR ≅ ∆POR
∴ ∠BOR = ∠POR
এখন, ∠AOQ+∠QOR+∠POR+∠BOR=180°
বা, ∠POQ+∠POQ+∠POR+∠POR=180° [যেহেতু,∠AOQ=∠POQএবং∠BOR=∠POR]
বা, 2∠POQ+2∠POR=180°
বা, 2(∠POQ+∠POR)=180°
বা, (∠POQ+∠POR)=90°
বা, ∠QOR=90°
∴ ∆QOR সমকোণী ত্রিভুজে যার ∠QOR সমকোণ এবং সমকৌণিক বিন্দু O থেকে অতিভুজ QR এর উপর OP লম্ব । যেহেতু সমকোণী ত্রিভুজের সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে লম্বের উভয়পার্শ্বে যে দুটি ত্রিভুজ উৎপন্ন হয় তারা পরস্পর সদৃশ ।
∴ ∆OPQ এবং ∆RPO সদৃশকোণী।যেহেতু, সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতী,
বা, OP2 = PQ.PR
বা, r2 = PQ.PR [যেহেতু OP=r একক]
∴ r2 = PQ.PR [ প্রমাণিত ]
সদৃশতা কষে দেখি ১৮.৪|Koshe Dekhi 18.4
4. AB কে ব্যাস করে একটি অর্ধবৃত্ত অঙ্কন করেছি । AB-এর উপর যেকোনো বিন্দু C থেকে AB এর উপর লম্ব অঙ্কন করেছি যে অর্ধবৃত্তকে D বিন্দুতে ছেদ করেছে । প্রমাণ করি যে, CD, AC ও BC এর মধ্য সমানুপাতী ।
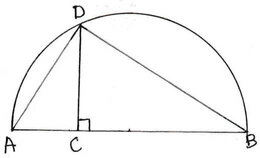
সমাধানঃ AB কে ব্যাস করে একটি অর্ধবৃত্ত অঙ্কন করা হয়েছে । AB এর উপর যে- কোনো বিন্দু C থেকে AB এর উপর একটি লম্ব CD অঙ্কন করা হয়েছে যা অর্ধবৃত্তকে D বিন্দুতে ছেদ করে ।প্রমাণ করতে হবে যে , CD, AC ও BC এর মধ্য সমানুপাতী । অর্থাৎ প্রমাণ করতে হবে যে CD2=AC.BC
অঙ্কনঃ A,D এবং B,D যুক্ত করা হল ।
প্রমাণঃ ∠ADB = 90° [যেহেতু,অর্ধবৃত্তস্থ কোন 1সমকোণ ]
∴ সমকৌণিক বিন্দু D থেকে অতিভুজ AB এর উপর DC লম্ব । যেহেতু, সমকোণী ত্রিভুজের সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে লম্বের উভয়পার্শ্বে যে দুটি ত্রিভুজ উৎপন্ন হয় তারা পরস্পর সদৃশ ।
∴ ∆ADC এবং ∆DBC সদৃশকোণী।যেহেতু, সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতী,
বা, CD2 = AC.BC [ প্রমাণিত ]
∴ CD, AC ও BC-এর মধ্যসমানুপাতী ।
সদৃশতা কষে দেখি ১৮.৪|Koshe Dekhi 18.4
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
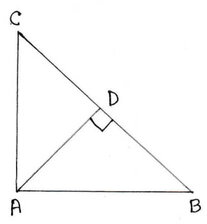
প্রমাণঃ ABC সমকোণী ত্রিভুজের BAC সমকোণ এবং সমকৌণিক বিন্দু A থেকে BC এর উপর AD লম্ব । যেহেতু সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে লম্বের উভয়পার্শ্বে যে দুটি ত্রিভুজ উৎপন্ন হয় তারা পরস্পর সদৃশ এবং প্রত্যেকটি ত্রিভুজ মূল ত্রিভুজের সাথে সদৃশ ।
∴ ∆ABC এবং ∆DAC সদৃশকোণী।যেহেতু, সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতী,
সদৃশতা কষে দেখি ১৮.৪|Koshe Dekhi 18.4
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
6.O কেন্দ্রীয় বৃত্তের AB ব্যাস । A বিন্দু দিয়ে অঙ্কিত একটি সরলরেখা বৃত্তকে C বিন্দুতে এবং B বিন্দুতে অঙ্কিত স্পর্শককে D বিন্দুতে ছেদ করে । প্রমাণ করি যে ,
(i) BD2 = AD.DC
(ii) যে- কোনো সরলরেখার জন্য AC এবং AD দ্বারা গঠিত আয়তক্ষেত্রের ক্ষেত্রফল সর্বদা সমান ।
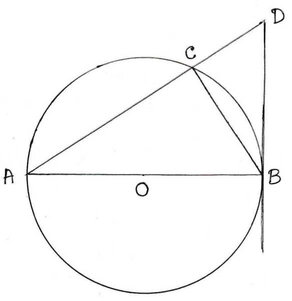
O কেন্দ্রীয় বৃত্তের AB ব্যাস । A বিন্দু দিয়ে অঙ্কিত একটি সরলরেখা বৃত্তকে B বিন্দুতে এবং B বিন্দুতে অঙ্কিত স্পর্শককে D বিন্দুতে ছেদ করে । প্রমাণ করতে হবে যে , (i) BD2 = AD.DC এবং (ii) যে- কোনো সরলরেখার জন্য AC এবং AD দ্বারা গঠিত আয়তক্ষেত্রের ক্ষেত্রফল সর্বদা সমান,অর্থাৎ প্রমাণ করতে হবে যে যেকোনো সরলরেখার ক্ষেত্রে (AC✕AD) সর্বদা নির্দিষ্ট ।
অঙ্কনঃ B,C যুক্ত করা হল ।
প্রমাণঃ ACB = 90° [ অর্ধবৃত্তস্থ কোণ 1 সমকোণ ]
∴ BC ⊥ AD
আবার,AB হল বৃত্তের ব্যাস এবং B বিন্দুতে BD স্পর্শক ।
∴ ABD = 90°
∴ ABD সমকোণী ত্রিভুজের সমকৌণিক বিন্দু থেকে অতিভুজ AD এর উপর BC লম্ব টানা হয়েছে । যেহেতু সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে লম্বের উভয়পার্শ্বে যে দুটি ত্রিভুজ উৎপন্ন হয় তারা পরস্পর সদৃশ এবং প্রত্যেকটি ত্রিভুজ মূল ত্রিভুজের সাথে সদৃশ ।
∴ ABD এবং BCD সদৃশকোণী।যেহেতু, সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতী,
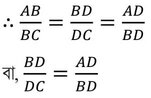
বা, BD2 = AD.DC [(i) নং প্রমাণিত ]
ABD সমকোণী ত্রিভুজের সমকৌণিক বিন্দু থেকে অতিভুজ AD এর উপর BC লম্ব টানা হয়েছে । যেহেতু সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে লম্বের উভয়পার্শ্বে যে দুটি ত্রিভুজ উৎপন্ন হয় তারা পরস্পর সদৃশ এবং প্রত্যেকটি ত্রিভুজ মূল ত্রিভুজের সাথে সদৃশ ।
∴ ABD এবং ACB সদৃশকোণী।যেহেতু, সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতী,
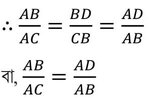
বা, AB2 = AC✕AD
সুতরাং AC ও AD বাহু দ্বারা গঠিত আয়তক্ষেত্রের ক্ষেত্রফল বৃত্তের ব্যাসের উপর অবস্থিত বর্গক্ষেত্রের ক্ষেত্রফলের সমান। ∴ যেকোনো সরলরেখার জন্য AC ও AD বাহু দ্বারা গঠিত আয়তক্ষেত্রের ক্ষেত্রফল সমান [(ii) নং প্রমাণিত ]
সদৃশতা কষে দেখি ১৮.৪|Koshe Dekhi 18.4
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
7. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q)
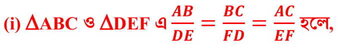
(a) ∠B=∠E
(b) ∠A=∠D
(c) ∠B=∠D
(d) ∠A=∠F
Ans: (c) ∠B=∠D
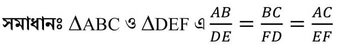
∴ ∆ABC এবং ∆EDF পরস্পর সদৃশ।
∴ ∠B=∠D , ∠A=∠E এবং ∠C =∠F [যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ কোণগুলি সমান]
∴ ∠B=∠D [উত্তর]
WBBSE Class 10 Math Solution Of Chapter 18 Similarity|Koshe Dekhi 18.4|সদৃশতা কষে দেখি ১৮.৪
(ii) ∆DEF ও ∆PQR –এ ∠D=∠Q এবং ∠R=∠E হলে, নীচের কোনটি সঠিক নয় লিখি ।
Ans: b
সমাধানঃ ∆DEF ও ∆PQR –এ ∠D=∠Q এবং ∠R=∠E
∴ ∠F=∠P [অবশিষ্ট কোণ ]
∴ ∆DEF ও ∆QRP পরস্পর সদৃশকোণী ।
∴ DE/QR=EF/RP=DF/PQ
∴ QR/PQ=EF/DF সঠিক নয় ।
সদৃশতা কষে দেখি ১৮.৪|Koshe Dekhi 18.4
(iii) ∆ABC ও ∆DEF ত্রিভুজে ∠A=∠E=40°, AB:ED=AC:EF এবং ∠F = 65° হলে , ∠B এর মান
(a) 35°
(b) 65°
(c) 75°
(d) 85°
Ans: (c) 75°
সমাধানঃ ∆ABC ও ∆DEF ত্রিভুজে ∠A=∠E=40°, AB:ED=AC:EF.
∴ ∆ABC এবং ∆EDF সদৃশকোণী।যেহেতু, সদৃশকোণী ত্রিভুজের অনুরূপ কোণগুলি সমান,
∴∠A=∠E, ∠B=∠D এবং ∠C=∠F
আবার,∠A=∠E=40° এবং ∠F=65°
∴ ∠C =65° [যেহেতু,∠C=∠F]
∴ ∠B=180°-(∠A+∠C)=180°-(40°+65°)=180°-105°=75°
∴ ∠B=75°
সদৃশতা কষে দেখি ১৮.৪|Koshe Dekhi 18.4
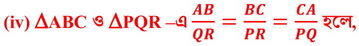
(a) ∠A=∠Q
(b) ∠A=∠P
(c ) ∠A=∠R
(d) ∠B=∠Q
Ans: (a) A=Q
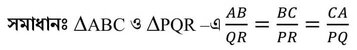
∴ ∆ABC এবং ∆QRP পরস্পর সদৃশ।
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ কোণগুলি সমান
∴ ∠A =∠Q , ∠B=∠R এবং ∠C =∠P
সদৃশতা কষে দেখি ১৮.৪|Koshe Dekhi 18.4
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
(v) ABC ত্রিভুজে AB=9 সেমি., BC=6 সেমি. এবং CA=7.5 সেমি. । ∆DEF ত্রিভুজে BC বাহুর অনুরূপ বাহু EF ; EF=8সেমি. এবং ∆DEF সদৃশ ∆ABC হলে ∆DEF এর পরিসীমা
(a) 22.5 সেমি.
(b) 25 সেমি.
(c ) 27 সেমি.
(d) 30 সেমি.
Ans: (d) 30 সেমি.
সমাধানঃ ∆DEF সদৃশ ∆ABC ( প্রদত্ত)।যেহেতু, সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতী,
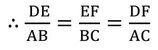
যেহেতু, AB=9 সেমি., BC=6 সেমি.,CA=7.5 সেমি এবং EF=8সেমি ।
∴ ∆DEF ত্রিভুজের পরিসীমা (DE+EF+DF)= ( 12+8+10)সেমি. =30 সেমি.
সদৃশতা কষে দেখি ১৮.৪|Koshe Dekhi 18.4
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখিঃ
(i) দুটি চতুর্ভুজের অনুরূপ কোণগুলি সমান হলে চতুর্ভুজ দুটি সদৃশ ।
উত্তরঃ মিথ্যা
(ii) পাশের চিত্রে ∠ADE = ∠ACB হলে , ∆ADE সদৃশ ∆ACB
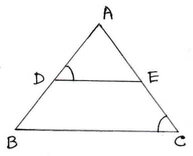
উত্তরঃ সত্য
সমাধানঃ∆ADE এবং ∆ABC-এর ক্ষেত্রে,
∠ADE = ∠ACB
∠DAE = ∠BAC [ একই কোণ ]
এবং ∠AED = ∠ABC [ অবশিষ্ট কোণ ]
∆ADE এবং ∆ACB পরস্পর সদৃশকোণী ।
সদৃশতা কষে দেখি ১৮.৪|Koshe Dekhi 18.4
(iii) ∆PQR –এর QR বাহুর উপর D এমন একটি বিন্দু যে , PD ⊥ QR ; সুতরাং ∆PQD সদৃশ ∆RPD
উত্তরঃ মিথ্যা
যেহেতু সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে লম্বের উভয়পার্শ্বে যে দুটি ত্রিভুজ উৎপন্ন হয় তারা পরস্পর সদৃশ এবং প্রত্যেকটি ত্রিভুজ মূল ত্রিভুজের সাথে সদৃশ ।সুতরাং ∆PQD সদৃশ ∆RPD হতে গেলে ∠P সমকোণ হতে হত ।
WBBSE Class 10 Math Solution Of Chapter 18 Similarity|Koshe Dekhi 18.4|সদৃশতা কষে দেখি ১৮.৪
(C ) শূন্যস্থান পূরণ করিঃ
(i) দুটি ত্রিভুজ সদৃশ হবে যদি তাদের _________ বাহুগুলি সমানুপাতী হয় ।
উত্তরঃ অনুরূপ
(ii) ∆ABC ও ∆DEF –এর পরিসীমা যথাক্রমে 30 সেমি. ও 18 সেমি. । ∆ABC সদৃশ ∆DEF; BC ও EF অনুরূপ বাহু । যদি BC = 9 সেমি. হয় , তাহলে EF = _________ সেমি.
উত্তরঃ 5.4 সেমি.
সমাধানঃ ∆ABC সদৃশ ∆DEF ( প্রদত্ত )।যেহেতু, সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতী,
সদৃশতা কষে দেখি ১৮.৪|Koshe Dekhi 18.4
8. সংক্ষিপ্ত উত্তর ধর্মী প্রশ্ন (S.A)
(i) পাশের চিত্রে, ∠ACB =∠BAD এবং AD ⊥ BC ; AC=15 সেমি.,AB=20সেমি., এবং BC=25 সেমি. হলে, AD এর দৈর্ঘ্য কত তা লিখি ।
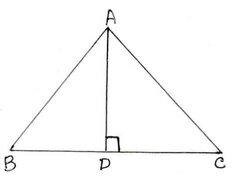
সমাধানঃ ∠ACB =∠BAD এবং AD ⊥ BC ; AC=15 সেমি.,AB=20সেমি.,এবং BC=25 সেমি. হলে, AD এর দৈর্ঘ্য নির্ণয় করতে হবে ।
∆ABC এবং ∆ABD ত্রিভুজের ক্ষেত্রে ,
∠BAC = ∠ADB [উভয়ই 90°]
∠ACB =∠BAD [প্রশ্নানুসারে]
∠ABD = ∠ABC [একই কোণ]
∴ ∆ABC এবং ∆DBA সদৃশকোণী।যেহেতু, সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতী,
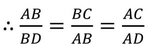
বা, 25AD = 300
বা, AD = 300/25
বা, AD = 12
∴ AD এর দৈর্ঘ্য 12 সেমি.।
সদৃশতা কষে দেখি ১৮.৪|Koshe Dekhi 18.4
(ii) পাশের চিত্রে ∠ABC=90° এবং BD ⊥ AC;যদি AB=30সেমি.,BD=24সেমি., এবং AD=18সেমি. হলে, BC এর দৈর্ঘ্য কত হিসাব করে লিখি ।
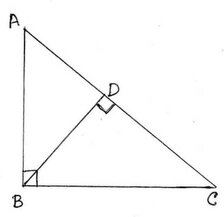
সমাধানঃ ABC ত্রিভুজে ∠ABC = 90° এবং সমকৌণিক বিন্দু B থেকে অতিভুজ AC এর উপর BD লম্ব । যেহেতু সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে লম্বের উভয়পার্শ্বে যে দুটি ত্রিভুজ উৎপন্ন হয় তারা পরস্পর সদৃশ এবং প্রত্যেকটি ত্রিভুজ মূল ত্রিভুজের সাথে সদৃশ ।
∴ ∆ABC এবং ∆BDC পরস্পর সদৃশ । আবার , ∆ABD এবং ∆BCD পরস্পর সদৃশ ।
যেহেতু , ∆ABD এবং ∆BCD সদৃশকোণী।যেহেতু, সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতী,
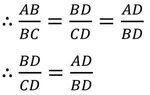
বা, BD2 = AD✕CD
বা, (24)2=18✕CD [যেহেতু ,BD=24সেমি.,এবংAD=18সেমি.]
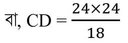
বা, CD = 32
আবার যেহেতু , ∆ABC এবং ∆BDC সদৃশকোণী।যেহেতু, সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতী,
বা, 24BC= 960
বা, BC = 960/24
বা, BC = 40
∴ BC-এর দৈর্ঘ্য 40 সেমি.।
সদৃশতা কষে দেখি ১৮.৪|Koshe Dekhi 18.4
(iii) পাশের চিত্রে, ∠ABC =90° এবং BD ⊥ AC ; যদি BD=8সেমি. এবং AD=4 সেমি. হয়, তাহলে CD এর দৈর্ঘ্য কত তা লিখি ।
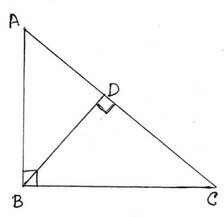
সমাধানঃ এক্ষেত্রে , ∠ABC =90° এবং সমকৌণিক বিন্দু থেকে অতিভুজ AC এর উপর BD লম্ব । যেহেতু সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে লম্বের উভয়পার্শ্বে যে দুটি ত্রিভুজ উৎপন্ন হয় তারা পরস্পর সদৃশ ।
∴ ∆ABD এবং ∆BCD সদৃশকোণী।যেহেতু, সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতী,
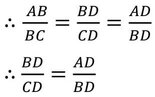
বা, BD2 = CD✕AD
বা, (8)2 = CD✕4 [ যেহেতু, BD=8 সেমি.,AD=4সেমি.]
বা, 4CD =64
বা, CD=64/4
বা, CD = 16
∴CD-এর দৈর্ঘ্য 16 সেমি.।
সদৃশতা কষে দেখি ১৮.৪|Koshe Dekhi 18.4
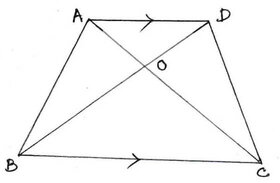
∆AOD ও ∆COB এর ক্ষেত্রে ,
∠OAD = ∠OCD [ একান্তর কোণ,যেহেতু, AD||BC এবং AC ভেদক ]
আবার,∠ODA=∠OCB [একান্তর কোণ,যেহেতু,AD||BC এবং DB ভেদক ]
∠AOD=∠BOC [বিপ্রতীপ কোন]
∴ ∆AOD এবং ∆COB সদৃশকোণী।
যেহেতু, সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতী,
সদৃশতা কষে দেখি ১৮.৪|Koshe Dekhi 18.4
(v) ∆ABC সদৃশ ∆DEF এবং ∆ABC ও ∆DEF –এ AB,BC ও CA বাহুর অনুরূপ বাহুগুলি যথাক্রমে DE,EF ও DF; ∠A =47° এবং ∠E = 83° হলে , ∠C এর পরিমাপ কত ?
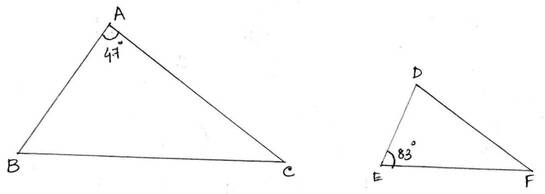
সমাধানঃ ∆ABC সদৃশ ∆DEF এবং ∆ABC ও ∆DEF –এ AB,BC ও CA বাহুর অনুরূপ বাহুগুলি যথাক্রমে DE,EF ও DF.
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ কোণগুলি সমান
∴ ∠A=∠D ,∠B=∠E এবং ∠C =∠F
∴ ∠A=∠D=47° এবং ∠B=∠E = 83°
∴ ∠C = 180°-(∠A+∠B) = 180°-(47°+83°)=180°-130°=50°
∴ ∠C=50°
সদৃশতা কষে দেখি ১৮.৪|Koshe Dekhi 18.4
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন