SN Dey Solution For Class 12 Mapping or Function.SN Dey Math Mapping or Function.ক্লাস ১২ চিত্রণ বা অপেক্ষক সমাধান ।
SN Dey Solution For Class 12 Mapping or Function|চিত্রণ বা অপেক্ষক সমাধান
প্রশ্নমালা 2A
অতি সংক্ষিপ্ত উত্তরধর্মীঃ
1(i) মনে করো A= {a,b}; A সেটের ওই একি সেটে সব এক এক চিত্রণসমূহ গুলি লেখ ।
(ii) মনে করো A={1,2,3}; A সেটের ওই একি সেটে সব এক এক চিত্রণ সমূহ লেখ।
সমাধানঃ (i) f(a)=a, f(b)=b, এবং f(a)=b , f(b)=a
এই গুলি হলও A সেট থেকে A সেটের অপর সব এক এক চিত্রণ ।
(ii) f(1)=1, f(2)=2 , f(3)=3;
f(1)=1 , f(2)=3 , f(3)=2;
f(1)=2 , f(2)=1, f(3)=3;
f(1)=3 , f(2)=2, f(3)=1;
f(1)=2, f(2)=3, f(3)=1;
f(1)=3, f(2)=1, f(3)=2
উপরি উক্ত চিত্রণ গুলি A সেট থেকে A সেটের ওপর এক এক চিত্রণ ।
SN Dey Solution For Class 12 Mapping or Function
2. মনে করো A={0,1} , B={2,6} এবং f:A→B , B চিত্রণ f(x)=6-4x দ্বারা ও g:A→B চিত্রণ g(x)= x²-5x+6 দ্বারা সংজ্ঞাত , f=g কিনা যুক্তি সহ বল ।
সমাধান ঃ এক্ষেত্রে f(0)=6-4(0)=6 এবং f(1)=6-4(1)=2
∴ f(0)=6 , f(1)=2
আবার g(0)= 0²-5(0)+6=6
এবং g(1)= 1²-5(1)+6=2
∴ g(0)=6 , g(1)=2
∴ f=g
SN Dey Solution For Class 12 Mapping or Function
3.মনে করো সব x ∊R এর জন্য f:R → R চিত্রণ f(x)= x²+1 দ্বারা সংজ্ঞাত দেখাও যে f চিত্রণ এক এক বা উপরি চিত্রণ নয় ।
সমাধান ঃ (1,-1)∊ R
f(-1)=(-1)²+1=1+1=2
f(1)= 1²+1=2
-1≠1⇒f(-1)=f(1)
এক এক চিত্রণ এর শর্ত হলও x1≠x2 ⇒f(x1 )≠ f (x2 )
এক্ষেত্রে এই শর্ত টি প্রযোজ্য নয় ।
∴ চিত্রণ টি এক এক চিত্রণ নয় ।
ধরাযাক , x²+1=y
বা, X= √y-1
স্পষ্টতই y<1 হলে x ∉R (domain)
∴ codomain R এর মধ্যে 1 অপেক্ষা ছোট কোনও বাস্তব সংখ্যার প্রাগবিম্ব ক্ষেত্র(domain) R এর মধ্যে নেই
∴ f(R )≠ R(codomain)
স্পষ্টতই f(R)⊆ R
∴ চিত্রণ টি উপরি চিত্রণ নয় ।
SN Dey Solution For Class 12 Mapping or Function
4.মনে করো f: R → R চিত্রণ f(x)=3x³+4 দ্বারা সংজ্ঞাত । দেখাও যে f হলও R থেকে ওই সেট এ একটি এক এক উপরিচিত্রণ ।
সমাধান ঃ ধরি (x1 , x2)∈ R
এবং f(x1)≠ f (x2 )
f(x1)≠ f (x2 )⇒ 3x1³+4 ≠ 3x2³+4
⇒ x1³ ≠ x2³
⇒x1 ≠ x2
∴ f(x1)≠ f (x2 )⇒ x1 ≠ x2 for all (x1 , x2)∈ R
∴ f চিত্রণ টি একটি এক এক চিত্রণ ।
ধরি y ∈R (co-domain / উপ-অঞ্চল)
এবং f(x)=y
∴ y=3x³+4
বা,{(y-4)/3}= x³
∴ f এর co domain এর যেকোনো পদের প্রাগবিম্ব domain R এ বর্তমান
∴ f (R ) = codomain set R
∴ f চিত্রণ টি একটি উপরি চিত্রণ ।
∴ f চিত্রণ টি একটি এক এক উপরি চিত্রণ ।
SN Dey Solution For Class 12 Mapping or Function
5.মনে করো A= {-1,1,2,-3},B={2,8,18,32} এবং f:A → B চিত্রণ f(x)= 2x² দ্বারা সংজ্ঞাত দেখাও যে f হলও একটি বহু একক চিত্রণ ।
সমাধানঃ
f(-1)=2(-1)²= 2
f(1)= 2(1)²=2
-1 এবং 1 এর দুটি প্রতিবিম্ব একই
∴ f(x1)=f(x2)⇒x1≠x2 ∀ x1,x2 ∈A
অতএব চিত্রণ টি একটি বহু একক চিত্রণ ।
SN Dey Solution For Class 12 Mapping or Function
6.(i) প্রমান করো যে f:R → R চিত্রণ যা f(x)=cosx দ্বারা সংজ্ঞাত (সব x∈R এর জন্য ) এক এক কিম্বা উপরি চিত্রণ নয় ।
সমাধানঃ ধরি x1 ,x2 ∈R
এবং f(x1)=f(x2)⇒cosx1=cosx2⇒x1=2nπ±x2 , n∈z
উপরের সমীকরণ টির অসংখ্য সমাধান আছে
অতএব চিত্রণ টি একটি বহু একক চিত্রণ এক এক চিত্রণ নয় ।
আমরা জানি cosx এর পাল্লা {-1,1}, এটি R এর উপসেট
এক্ষেত্রে f(R )⊆ R
অতএব চিত্রণ টি উপরি চিত্রণ নয় ।
SN Dey Solution For Class 12 Mapping or Function
6(ii)দেখাও যে modulus function f:R → R যা f(x)=∣x∣ দ্বারা প্রদত্ত । তা এক এক কিম্বা উপরি চিত্রণ নয়,
এখানে ∣x∣ = x যখন x ≥ 0
= -x যখন x ≤ 0
সমাধানঃ
-1 ,1 ∈R এবং f(-1)= 1 ও f(1)=1
∴ -1≠1 ⇒f(-1)=f(1)
∴ f চিত্রণ টি এক এক চিত্রণ নয় ।
আবার -1 ∈ R (co-domain set)
কিন্তু f(x)= ∣x∣ (non negative number)
∴ -1 এর জন্য কোনও প্রাগবিম্ব domain set R এর মধ্যে পাওয়া যায়ে না , এমনকি কোনও ঋণাত্মক সংখ্যার প্রাগবিম্ব পাওয়া যায়ে না ।
∴ f(R )⊆ R
সুতরাং f চিত্রণ টি উপরি চিত্রণ নয় ।
SN Dey Solution For Class 12 Mapping or Function
7. দেখাও যে f:N →N চিত্রণ যা f(x)=3x দ্বারা সংজ্ঞাত , N সেটে ওই একি সেটের একটি এক এক চিত্রণ কিন্তু উপরি চিত্রণ নয় ।
সমাধানঃ ধরি x1 , x2 ∈ R
এবং f(x1)=f(x2)
f(x1)=f(x2) ⇒3x1=3x2⇒x1=x2
∴ f(x1)=f(x2)⇒ x1=x2
সুতরাং f চিত্রণ টি একটি এক এক চিত্রণ ।
এখন 1∈ N (co-domain set)
∴ 3x=1⇒ x=1/3 ∉ N (domain set N)
∴ ∀ y∈ N (co-domain set) ∌ x∈ N (domain set)
f(N)⊆ N
সুতরাং f একটি উপরি চিত্রণ নয় ।
SN Dey Solution For Class 12 Mapping or Function
8.প্রমান করো যে f:R → R চিত্রণ যা f(x)=x³+3x দ্বারা সংজ্ঞাত , R সেটে ওই একই সেটের একটি bijection ।
সমাধানঃ
ধরি x,y ∈R such that f(x)=f(y)
f(x)=f(y)⇒x³+3x= y³+3y
⇒ x³+3x- y³-3y=0
⇒ x³- y³+3x-3y=0
⇒ (x-y)(x²+xy+y²)+3(x-y)=0
⇒ (x-y)( x²+xy+y²+3)=0
⇒(x-y){x²+2x(y/2)+(y/2)²+3+y²-(y/2)²}=0
⇒ (x-y){(x+y/2)²+3+3y²/4}=0
দুটি রাশির গুনফল শূন্য এবং {(x+y/2)²+3+3y²/4}>0
∴ (x-y)=0 ⇒ x=y
∴ f(x)=f(y)⇒x=y
সুতরাং f চিত্রণ টি এক এক চিত্রণ ।
আবার ধরা যাক y∈ R
এবং y=f(x)=x³+3x ⇒x³+3x-y=0
যেহেতু সমীকরণ টি একটি ত্রিঘাত সমীকরণ
সুতরাং একটি বাস্তব বীজ থাকবে
ধরাযাক বাস্তব বীজ টি হলও a
∴ a³+3a-y=0
⇒ a³+3a=y
⇒ f(a)=y
∴ যে কোনও y∈ R এর জন্য প্রাগবিম্ব a∈R পাওয়া যাবে ।
∴ f চিত্রণ টি একটি উপরি চিত্রণ
সুতরাং f চিত্রণ টি একটি এক এক উপরি চিত্রণ অর্থাৎ bijection ।
SN Dey Solution For Class 12 Mapping or Function
9.মনে করো A একটি সসীম সেট । যদি f:A→ A একটি উপরি চিত্রণ হয় তবে দেখাও যে চিত্রণ টি এক -এক হবে।
সমাধানঃ f:A→ A চিত্রণ টি এক-এক চিত্রণ না হলে co-domain সেট A এর মধ্যে কমপক্ষ্মে একটি পদ খুজে পাওয়া যাবে যার প্রাগবিম্ব domain set A এর মধ্যে থাকবেনা । সেক্ষেত্রে f চিত্রণ টি উপরি চিত্রণ হবেনা ।
কিন্তু প্রদত্ত শর্তানুসারে f চিত্রণ টি একটি উপরি চিত্রণ ,
∴ f চিত্রণ টি এক-এক চিত্রণ ও হবেনা ।
SN Dey Solution For Class 12 Mapping or Function
সংক্ষিপ্ত উত্তরধর্মীঃ
1.মনে করো কোনও সমতলে অঙ্কিত সব চতুর্ভুজের সেট A এবং সব ধনাত্মক বাস্তব সংখ্যার সেট R+ ; প্রমান করো যে f:A → R+ চিত্রণ যা f(x)= চতুর্ভুজের ক্ষেত্রফল x দ্বারা সংজ্ঞাত, একটি বহু একক চিত্রণ ।
সমাধানঃ কোনও সমতলে দুটি চতুর্ভুজ Q1 এবং Q2 থাকতে পারে যাদের বাহুগুলো অসমান কিন্তু ক্ষেত্রফল সমান । সুতরাং Q1,Q2 ∈A এমন হওয়া সম্ভব যে f(Q1)=f(Q2), যখন Q1≠Q2
সুতরাং f একটি বহু-এক চিত্রণ ।মনে করো y হলও R+ সেটের যে কোনও পদ, তাহলে সর্বদাই কম করে একটি চতুর্ভুজ Q(ধরা হলও) পাওয়া যাবে যার ক্ষেত্রফল y বর্গ এককের সমান । সুতরাং সব y∈R+ এর জন্য কমপক্ষ্মে একটি চতুর্ভুজ Q ∈A পাওয়া যাবে যাতে f(Q)=y হয় ।
সুতরাং f(A)=R+
∴ f একটি উপরি চিত্রণ
অর্থাৎ f একটি বহু এক উপরিচিত্রণ ।
SN Dey Solution For Class 12 Mapping or Function
2. মনে করো A={-1,1,-2,2} , B={3,4,5,6} এবং f:A→ B চিত্রণ, f={(1,6),(-1,4),(2,3),(-2,5)} দ্বারা সংজ্ঞাত । প্রমান করো যে f একটি bijective mapping ।
সমাধানঃ f হলও B সেটে A সেটের একটি চিত্রণ ।
f(-1)=4, f(1)=6 ,f(-2)=5 এবং f(2)=3
∴ A সেটের স্বতন্ত্র পদ সমূহের জন্য B সেটে স্বতন্ত্র প্রতিবিম্ব আছে
সুতরাং, f একটি এক-এক চিত্রণ ।——————– (i)
আবার f চিত্রণের পাল্লা ={y:f(x)=y}={3,4,5,6}=B
∴ f(A)=B
∴ f চিত্রণ টি একটি উপরি চিত্রণ ।—————————–(ii)
f একটি এক-এক উপরিচিত্রণ ।
∴(i) ও (ii) থেকে বলতে পারি f একটি bijective mapping .
SN Dey Solution For Class 12 Mapping or Function
3.মনে করো D হলও সব বিজোড় স্বাভাবিক সংখ্যার সেট । দেখাও যে f:N → D চিত্রণ, যা f(x)=2x-3 দ্বারা সংজ্ঞাত একটি উপরিচিত্রন কিন্তু g:Z→Z চিত্রণ যা g(x)=2x-3 দ্বারা সংজ্ঞাত একটি উপরিচিত্রন নয় ।
সমাধানঃ f:N to D চিত্রণ f(x)=2x-3 দ্বারা সংজ্ঞাত
ধরি y ∈ co-domain set D(সকল বিজোড় সংখ্যার সেট )
স্পষ্টতই y একটি বিজোড় সংখ্যা
এবং f(x)=y
∴2x-3=y
X=(y+3)/2
যেহেতু y বিজোড় সংখ্যা ∴ x=(y+3)/2 ∈N
∴ প্রত্যেক y∈ D এর জন্য আমরা একটি x ∈ N খুঁজে পাই
∴ f(N)=D
সুতরাং f চিত্রণ টি একটি উপরিচিত্রণ ।
g:Z to Z চিত্রণ f(x)=2x-3 দ্বারা সংজ্ঞাত
ধরি y∈ Z (co-domain set)
এবং g(x)=y
∴2x-3=y
X=(y+3)/2
স্পষ্টতই যখন y জোড় সংখ্যা তখন (y+3)/2=x ∉ Z(domain)
∴ প্রত্যেক y∈ Z(co-domain) এর জন্য আমরা একটি x ∈Z(domain) খুঁজে পাইনা ।
অর্থাৎ g(z)≠z
সুতরাং g চিত্রণ টি উপরি চিত্রণ নয় ।
SN Dey Solution For Class 12 Mapping or Function
4.দেখাও যে f:R→ R চিত্রণ যা f(x)=mx+n (m,n,x ∈R এবং m≠0) দ্বারা সংজ্ঞাত একটি bijection.
সমাধানঃ ধরি x,y ∈R(domain ) such that f(x)=f(y)
f(x)=f(y) ⇒mx+n=my+n ⇒ mx=my ⇒x=y
∴ f একটি এক-এক চিত্রণ ।——————–(i)
ধরি y ∈ R(co-domain) এবং f(x)=y
∴ mx+n=y
বা, x=(y-n)/m
যেহেতু m,n ∈R এবং m≠0
∴ x=(y-n)/m R
সুতরাং প্রত্যেক y ∈R (codomain) এর জন্য একটি x ∈R(domain) খুঁজে পাবো ।
∴ f একটি উপরিচিত্রণ ———————-(ii)
(i) ও (ii) থেকে পাই f একটি bijection .
SN Dey Solution For Class 12 Mapping or Function
5.মনে করো A=R-{2} এবং B=R-{1}, দেখাও যে f:A→B অপেহ্মক যা f(x)=(x-3)/(x-2) দ্বারা সংজ্ঞাত, একটি bijection.
সমাধানঃ ধরা যাক x,y ∈A এমন যে f(x)=f(y)
এখন f(x)=f(y)
⇒(x-3)/(x-2)=(y-3)/(y-2)
⇒ (x-3)(y-2)=(y-3)(x-2)
⇒ xy-3y-2x+6=xy-3x-2y+6
⇒ -3y+2y=-3x+2x
⇒ -y=-x
⇒ x=y
∴ f(x)=f(y) ⇒ x=y
অর্থাৎ f চিত্রণ টি একটি এক-এক চিত্রণ ।
ধরাযাক y ∈ B এমন যে f(x)=y
∴ f(x)=y
⇒(x-3)/(x-2)=y
⇒ (x-3)=y(x-2)
⇒ x(1-y)=3-2y
⇒ x=(3-2y)/(1-y) [y≠1]
আবার (3-2y)/(1-y) ≠ 2 [যেহেতু (3-2y)/(1-y) = 2 ⇒3=2 যা অসম্ভব ]
∴ x=(3-2y)/(1-y) ∈A
∴ যে কোনও y ∈B এর জন্য প্রাগবিম্ব x ∈A তে খুঁজে পাওয়া যায়ে
সুতরাং f একটি উপরি চিত্রণ ।
∴ f একটি bijection .
SN Dey Solution For Class 12 Mapping or Function
6. মনে করো সব জতিল সংখ্যার সেট C এবং সব z∈C এর জন্য f:C → R চিত্রণ f(Z)= ∣z∣ দ্বারা সংজ্ঞাত, দেখাও যে f একটি এক-এক কিম্বা উপরিচিত্রণ নয় ।
সমাধানঃ
প্রদত্ত f(z)=∣z∣ সব Z ϵ C এর জন্য
Let z1=x+iy and z2=x−iy x,y ϵ R
প্রথম ধাপ: Injective or এক-এক অপেক্ষক:-
∣z1∣=x2+y2 এবং ∣z2∣=x2+y2
∴ ∣z1∣=∣z2∣
কিন্তু z1=z2
অর্থাৎ, f(z) এক-এক অপেক্ষক নয় ।
দ্বিতীয় ধাপ : Surjective or উপরিচিত্রণ :–
ধরি y ϵ R (co-domain)
ধরি, y= −2
y=-2 এর জন্য কোনও x∈C(domain) খুঁজে পাইনা যাতে ∣z∣= −2 হয়
∴ f অপেক্ষক টি উপরিচিত্রণ নয় ।
অর্থাৎ , f এক-এক এবং উপরি চিত্রণ কোনও টি নয় ।
SN Dey Solution For Class 12 Mapping or Function
6 signum function f:R → R নিম্নলিখিত ভাবে প্রদত্তঃ
f(x)= 1 যখন x>0
= 0 যখন x=0
= -1 যখন x<0
প্রমান করো যে f একটি এক-এক অপেক্ষক কিংবা উপরিচিত্রণ নয় ।
সমাধানঃ
এক্ষেত্রে 1,2 ∈ R এবং 1≠2 কিন্তু
f(1)=f(2)=1 [যেহেতু f(x)=1 যখন x>0]
সুতরাং 1≠2 ⇒ f(1)=f(2)
∴ f চিত্রণ টি এক-এক চিত্রণ নয় ।
আবার 5 ∈R (co-domain)
5 এর জন্য কোনও প্রাগবিম্ব x পাবনা যাতে f(x)=5 হয়
সুতরাং প্রত্যেক y ∈R(co-domain) এর জন্য আমরা প্রাগবিম্ব x ∈R(domain) পাবনা
∴ f চিত্রণ টি উপরি চিত্রণ নয় ।
SN Dey Solution For Class 12 Mapping or Function
7.মনেকরো , A={x∈R:-1 ≤ x ≤1}=B এবং f:A→ B চিত্রণ f(x)=x∣x∣ দ্বারা সংজ্ঞাত।দেখাও যে f চিত্রণটি bijective ।
সমাধানঃ মনে করো X ও y হলও A সেটের যেকোনো দুটি পদ ; তাহলে,
x ≠ y⇒ x∣x∣ ≠ y∣y∣ ⇒ f(x) ≠ f(y)
এখান থেকে বোঝা যায়ে যে B সেটে A সেটের f অপেক্ষ্ক টি injective .
আবার f অপেক্ষ্কের পাল্লা f(A) হলে
f(A)= {f(x) : x ∈A} = {x∈ R : -1 ≤ x ≤ 1 } = B
অর্থাৎ f অপেক্ষ্কের পাল্লা= তার উপ অঞ্চল । সুতরাং f অপেক্ষক টি surjective ।
যেহেতু B সেটে A সেটের f অপেক্ষক টি injective এবং surjective সুতরাং অপেক্ষক টি একটি bijection .
SN Dey Solution For Class 12 Mapping or Function
8.মনে করো A={x∈R : -1≤ x ≤ 1 }=B প্রমান করো যে f(x)=sinπx দ্বারা সংজ্ঞাত B সেটে A সেটের চিত্রণ টি surjective ।
সমাধানঃ স্পষ্টতই A=B=[-1,1]
∴ f:[-1,1] to [1,1] নিম্নরুপে সংজ্ঞাত
F(x)=sinπx for all x∈ [-1,1]
ধরাযাক y∈ [-1,1] (co-domain)
F(x)=y
⇒sinπx=y
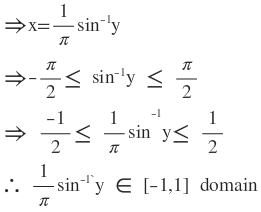
∴ f চিত্রণ টি surjective .
SN Dey Solution For Class 12 Mapping or Function
9(i).দেখাও যে f:N → N চিত্রণ যা নিম্নরুপে সংজ্ঞাত
F(x)= x+1 যখন x ∈N অযুগ্ম
= x-1 যখন x∈N যুগ্ম
একটি এক এক এবং উপরিচিত্রণ ।
সমাধানঃ যেহেতু সব n∈N এর জন্য আমরা পাই ,
F(n)= n-1 , যখন n∈N এবং n জোড়
= n+1, যখন n∈ N এবং n বিজোড়
মনে করো x ও y হলও N এর যেকোনো দুটি পদ, তাহলে যদি
(i) x ও y উভয়ই জোড় হয় তবে ,
f(x)=f(y)⇒ x-1=y-1⇒ x=y
(ii) যদি x ও y উভয়ই বিজোড় হয় তবে
f(x)=f(y)⇒ x+1=y+1 ⇒x=y
(iii) x জোড় এবং y বিজোড় হলে x≠y
X জোড় হওয়ায়ে f(x)= x-1(বিজোড়) এবং y বিজোড় হওয়ায়ে f(y)=y+1 (জোড় )
সুতরাং f(x)≠ f(y)
∴ x≠y ⇒ f(x)≠f(y) হয় ,
সুতরাং (i), (ii) ও (iii) থেকে পাই f চিত্রণ টি একটি এক-এক চিত্রণ ।
আবার f এর প্রদত্ত সংজ্ঞা থেকে পাই ,
f(1)=1+1=2
f(2)=2-1=1
f(3)=3+1=4
f(4)=4-1=3
∴ f এর পাল্লা ={f(n):n∈N}={f(1),f(2),f(3),f(4),……..}={2,1,4,3,….}=N
স্পষ্টতই f এর পাল্লা তার উপ অঞ্চল(N) এর সাথে সমান
সুতরাং f চিত্রণ টি একটি উপরিচিত্রণ
অর্থাৎ f চিত্রণ টি একটি এক-এক উপরিচিত্রণ
∴ f চিত্রণ টি একটি bijection .
SN Dey Solution For Class 12 Mapping or Function
9(ii). প্রমান করো যেবৃহত্তম অখণ্ড অপেক্ষক f:R→R যা f(x)=[x] দ্বারা সংজ্ঞাত একটি এক–এক কিংবা উপরিচিত্রণ নয় । এখানে [x] হলও বৃহত্তম অখণ্ড সংখ্যা যা x এর সমান বা তার চেয়ে ছোটো ।
সমাধানঃ 2, 5/2 ∈ R (domain)
এবং 2 ≠ 5/2
এখন [2]=[5/2]=2
⇒ f(2)=f(5/2)
∴ 2 ≠ 5/2 ⇒ f(2)=f(5/2)
সুতরানফ f চিত্রণ টি এক-এক চিত্রণ নয় ।
এখন [x] ∈Z for all x ∈R
∴ f(x) এর পাল্লা = z
∴ f এর পাল্লা ≠ R (co-domain)
∴ f চিত্রণ টি উপরি চিত্রণ নয় ।
SN Dey Solution For Class 12 Mapping or Function
প্রশ্নমালা-2B
অতিসংক্ষিপ্ত উত্তরধর্মী
1. দুটি চিত্রনের সংযোজন বলতে কি বোঝো ?
সমাধানঃ
মনে করো f: A → B এবং g:B →C দুটি চিত্রণ বা অপেক্ষক । এই দুটি অপেক্ষকের সংযোজন (composition) g∘f দিয়ে সূচিত করা হয় এবং g∘f বলতে বোঝায়ে যে ,
g∘f={(a,c) : a∈A , c∈C এবং একটি b পাওয়া যাবে যাতে f(a)=b ও f(b)=c হবে }
g∘f সম্বন্ধ টি একটি অপেক্ষক হবে যদি f চিত্রণের প্রসার (range) , g চিত্রণের ক্ষেত্র (domain) একটি উপসেট হয় যদি , Rf ⊆ Dg যেখানে Rf হলও f চিত্রণের প্রসার , Dg হলও g চিত্রণের ক্ষেত্র ।
এখন h = g∘f : A to C হলে h(x)= (g∘f ) x= g(f(x)), সকল x∈A এর জন্য ।
SN Dey Solution For Class 12 Mapping or Function
2.মনে করো A= {1,2,3,4} এবং f:A→A ও g:A → A চিত্রণ দুটি নিম্নরুপে সংজ্ঞাত ঃ
f(1)=3,f(2)=4, f(3)=2, f(4)=1 এবং g(1)=2 ,g(2)=4, g(3)=1, g(4)=3 .
তাহলে (i) (g∘f)(4) (ii) (f∘g)(1) (iii) (g∘f)(3) এবং (iv) (f∘ g)(2) নির্ণয় করো ।
সমাধানঃ
এক্ষেত্রে f(A)⊆ A (domain of g)
অর্থাৎ g∘f এবং f∘g দুটি চিত্রণ ই সংজ্ঞাত
(i) (g∘f) (4)= g(f(4))= g(1)= 2
∴ (g∘f)(4)=2
(ii) (f∘g)(1)= f(g(1))=f(2)=4
∴ (f∘g)(1)= 4
(iii) (g∘f)(3)=g(f(3))= g(2)=4
∴ (g∘f)(3)=4
(iv) (f∘g)(2)=f(g(2))=f(4)=1 .
∴ (f∘g)(2)=1
SN Dey Solution For Class 12 Mapping or Function
3.মনে করো f:R→ R এবং g:R → R অপেক্ষক দুটি যথাক্রমে f(x)=x² ও g(x)= x+3 দ্বারা সংজ্ঞাত (i) (f o g)(2) এবং (gof)(3)-এর মান নির্ণয় করো ।
সমাধানঃ
স্পষ্টতই f(R ) ⊆ domain g এবং g(R ) ⊆ domain of f
সুতরাং gof এবং fog দুটি চিত্রণ ই সংজ্ঞাত
এখন fog(2)= f(g(2))= f(2+3)=f(5)= 5²=25 [ যেহেতু f(x)=x² ও g(x)= x+3 ]
gof(3)=g(f(3))=g(3²)= g(9)=9+3=12 [ যেহেতু f(x)=x² ও g(x)= x+3 ]
SN Dey Solution For Class 12 Mapping or Function
4. মনে করো f:R → R এবং g:R → R অপেক্ষক দুটি যথাক্রমে f(x)=2x+1 ও g(x)= x²-2 দ্বারা সংজ্ঞাত । gof এবং fog নির্ণয় করো ।
সমাধানঃ
এক্ষেত্রে f(R ) ⊆ domain g এবং g(R ) ⊆ domain f
সুতরাং gof এবং fog দুটি চিত্রণ ই সংজ্ঞাত
এখন gof(x)= g(f(x))= g(2x+1)=(2x+1)²-2= 4x²+4x-1
এবং fog(x)=f(g(x)) = f(x²-2)= 2(x²-2)+1= 2x²-4+1= 2x²-3
SN Dey Solution For Class 12 Mapping or Function
5. মনে করো f:R → R এবং g:R → R চিত্রণ দুটি যথাক্রমে f(x)= sinx এবং g(x)= x² দ্বারা সংজ্ঞাত , দেখাও যে gof ≠ fog ।
সমাধানঃ
এক্ষেত্রে f(R ) ⊆ domain g এবং g(R ) ⊆ domain f
সুতরাং gof এবং fog দুটি চিত্রণ -ই সংজ্ঞাত
এখন gof(x)=g(f(x))=g(sinx)= sin² x
আবার fog(x)= f(g(x))=f (x²)= sinx²
যেহেতু sin²x ≠ sinx²
অর্থাৎ (gof) ≠ (fog)
SN Dey Solution For Class 12 Mapping or Function
6. মনে কপর f:R → R এবং g:R→ R চিত্রণ দুটি যথাক্রমে f(x)= x+1 এবং g(x)= x-1 দ্বারা সংজ্ঞাত । প্রমান করো যে gof = fog = IR
সমাধানঃ
এক্ষেত্রে f(R )⊆ R [ g এর ক্ষেত্র (domain g)]
এবং g(R ) ⊆ R [f এর ক্ষেত্র (domain of f)]
সুতরাং gof এবং fog দুটি চিত্রণ-ই সংজ্ঞাত
এখন gof (x)= g(f(x))= g(x+1)= x+1-1= x
এবং fog (x)= f(g(x))=f(x-1)=x-1+1=x
∴ gof (x) =x , for all x∈R
এবং fog (x) = x , for all x ∈R
সুতরাং gof=fog= IR
SN Dey Solution For Class 12 Mapping or Function
7. ম
সমাধানঃ
fof = IR
∴ fof(x)=x , for all x∈R
⇒ f(f(x))=x , for all x ∈R
⇒ f(ax+b)=x, for all x∈R
⇒ a(ax+b)+b=x , for all x ∈R
⇒ a²x +ab+b =x , for all x∈ R
এটি একটি অভেদ ।
∴ a² =1
বা, a = ± 1
যখন a=1 , b=0
কিন্তু a=-1 হলে ab+b =0 সমীকরণ টি একটি অভেদ এ পরিনত হয় ।
∴ a=1 এবং b= 0
SN Dey Solution For Class 12 Mapping or Function
8. মনে করো সব x ∈ Q এর জন্য f:Q → Q চিত্রণ f(x)=2x+5 দ্বারা সংজ্ঞাত । যদি (gof)=IQ হয় তবে g:Q → Q চিত্রণ নির্ণয় করো ।
সমাধানঃ
প্রদত্ত f:Q → Q f(x)= 2x+5 দ্বারা সংজ্ঞাত
এবং gof = IQ
∴ gof(x)=x , for all x∈Q
⇒ g(f(x)) = x for all x∈ Q
⇒ g(2x+5)= x for all x ∈ Q ——- (i)
ধরাযাক 2x+5 =y
∴ x = (y-5)/2
(i) থেকে পাই g(y)= (y-5)/2 for all y ∈Q
∴ g(x)= (x-5)/2 for all x ∈Q
SN Dey Solution For Class 12 Mapping or Function
9. মনে করো f:R → R অপেক্ষক f(x)=4x-3 দ্বারা সংজ্ঞাত । যদি (gof)(x)=8x-1 হয় তবে g:R→ R অপেক্ষক টি নির্ণয় করো ।
সমাধানঃ
(gof)(x)= 8x-1
⇒g(f(x))= 8x-1
⇒ g(4x-3)=8x-1 —————- (i)
ধরি 4x-3=y ⇒ x= (y+3)/4
(i) থেকে পাই ,
g(y)= 8{(y+3)/4}-1=2y+6-1= 2y+5
∴ g(x)= 2x+5
∴ g:R to R অপেক্ষক টি , g(x)= 2x+5 দ্বারা সংজ্ঞাত
SN Dey Solution For Class 12 Mapping or Function
10.মনে করো f:R → R চিত্রণ f(x)= x+1 দ্বারা সংজ্ঞাত । (gof)(x)= x²+3x+3 হয় তবে g:R → R চিত্রণ নির্ণয় করো ।
সমাধানঃ
(gof) (x)= x²+3x+3
⇒ g(f(x))= x²+3x+3
⇒ g(x+1)= x²+3x+3
ধরাযাক y = x+1⇒ x = y-1
∴ g(y) = (y-1)²+3(y-1)+3
= y²-2y+1+3y-3+3
= y²+y+1
∴ g(x) = x²+x+1
∴ g: R to R চিত্রণ টি g(x) = x²+x+1 দ্বারা সংজ্ঞাত ।
SN Dey Solution For Class 12 Mapping or Function
সংক্ষিপ্ত উত্তরধর্মীঃ
1. মনে করো f:R → R এবং g:R → R চিত্রণ দুটি যথাক্রমে f(x)=x²+3x+1 এবং g(x)= 2x-3 দ্বারা সংজ্ঞাত । (i) fof (ii) gog (iii) gof (iv) fog সংযোজক চিত্রণ গুলি যেসব সূত্র দ্বারা সংজ্ঞাত সেগুলি নির্ণয় করো ।
সমাধানঃ
f(x)= x² +3x+1 for all x∈R
এবং g(x)= 2x-3 , for all x∈R
(i) (fof) (x)= f(f(x))= f(x²+3x+1)
= (x²+3x+1)²+3(x²+3x+1)+1
= x4+9x²+1+6x3+6x+2x2+3x²+9x+3+1
= x4+6x3+14x2+15x+5
∴ (fof):R to R
যেখানে fof(x)= x4+6x3+14x2+15x+5 for all x∈R
(ii) (gog)(x)= g(g(x))= g(2x-3)= 2(2x-3)-3=4x-6-3=4x-9
∴ (gog):R to R
যেখানে (gog)(x)= 4x-9 for all x∈R
(iii) gof(x)= g(f(x)) =g(x²+3x+1)=2(x²+3x+1)-3= 2x²+6x+2-3= 2x²+6x-1
∴ (gof):R to R যেখানে
(gof)(x)= 2x²+6x-1 for all x∈R
(iv) (fog)(x)= f(g(x))=f(2x-3)=(2x-3)²+3(2x-3)+1=4x²-12x+9+6x-9+1=4x²-6x+1
∴ (gof):R to R যেখানে
(fog)(x)= 4x²-6x+1 for all x∈R
SN Dey Solution For Class 12 Mapping or Function
2. মনে করো f:R → R এবং g:R → R চিত্রণ দুটি f(x)=3x-2 এবং g:R to R চিত্রণ দুটি f(x)= 3x-2 এবং g(x)= 3∣x∣- x² দ্বারা সংজ্ঞাত । (i) (gof)(-1) (ii) fog(-2) (iii) gof(3) iv (fog)(4) নির্ণয় করো ।
সমাধানঃ
প্রদত্ত অপেক্ষক গুলি হলও f:R → R এবং g:R → R যা নিম্নরূপে সংজ্ঞাত,
f(x) = 3x-2 for all x∈R
এবং g(x)= 3∣x∣ – x² for all x∈R
(i) (gof)(-1) = g(f(-1))= g(3(-1)-2)=g(-3-2)=g(-5)= 3(5) – 5²= 15-25=-10
(ii) fog(-2) = f(g(-2))= f(3(2)- 2²)= f(6-4)=f(2)= 3(2)-2=6-2=4
(iii) gof(3) = g(f(3))= g(3(3)-2)= g(9-2)=g(7)= 3(7)- 7²=21-49=-28
(iv) (fog)(4) = f(g(4)) = f(3(4)-4²)=f(12-16)= f(-4)= 3(-4)-2=-12-2=-14
SN Dey Solution For Class 12 Mapping or Function
3.f:R → R এবং g:R → R দুটি অপেক্ষক এমন যে (gof)(x)= sin² x এবং (fog)(x)= sin(x² ) f(x) ও g(x) এর মান নির্ণয় করো ।
সমাধানঃ
প্রদত্ত অপেক্ষক দুটি হলও f:R → R এবং g:R → R নিম্নরুপে সংজ্ঞাত
(gof) (x)= sin² x এবং (fog)(x)= sin(x² )
এখন (gof)(x)= sin²x ⇒ g(f(x))= (sinx)² ——(i)
আবার (fog)(x)= f(g(x))= sin (x²) ——(ii)
(i) ও (ii) থেকে বুঝতে পারি g(x)= x² এবং f(x)= sinx ।
SN Dey Solution For Class 12 Mapping or Function
4. মনে করো f:R → R এবং g: R → R চিত্রণ দুটি যথাক্রমে f(x)= 3x+5 ও g(x)= x²-3x+2 দ্বারা সংজ্ঞাত । (i) (gof)(x²-1) (ii) (fog)(x+2) এর মান নির্ণয় করো ।
সমাধানঃ
প্রদত্ত অপেক্ষক দুটি হলও f:R to R এবং g: R to R
নিম্নরুপে সংজ্ঞাত f(x)= 3x+5 ও g(x)= x²-3x+2
(i) (gof)(x²-1)
= g[f(x²-1)]
=g[3(x²-1)+5]
= g(3x²+2)
= (3x2+2)2-3(3x2+2)+2
= 9x4+12x2+4-9x2-6+2
=9x4+3x2
(ii) (fog)(x)
= f[g(x+2)]
= f[(x+2)²-3(x+2)+2]
= f [ x²+4x+4-3x-6+2]
=f(x²+x)
=3(x²+x)+5
=3x²+3x+5
SN Dey Solution For Class 12 Mapping or Function
5.দুটি অপেক্ষক f এবং g নিম্নরুপে সংজ্ঞাতঃ
f={(1,2)(2,3),(3,4),(4,1)} এবং g= {(2,-1)(4,2),(1,-2),(3,4)} প্রমান করো যে gof সংজ্ঞাত কিন্তু (fog) সংজ্ঞাত নয় । (gof) –কে ক্রমিত জোড় সমূহের সেট রুপে নির্ণয় করো ।
সমাধান ঃ
f এর ক্ষেত্র(domain) ={1,2,3,4}
এবং f এর পাল্লা (range)= {2,3,4,1}
g এর ক্ষেত্র (domain) ={2,4,1,3}
এবং g এর পাল্লা (range of g) ={-1,2,-2,4}
যেহেতু f এর পাল্লা = g এর ক্ষেত্র ,
সুতরাং (gof) সংজ্ঞাত ।
যেহেতু g এর পাল্লা f এর ক্ষেত্রের উপসেট নয় সেহেতু (fog) অসঙ্গাত ।
(gof) এর ক্রমিত জোড় গুলি হলও –
(gof)(1)= g[f(1)]=g(2)=-1
∴ক্রমিত জোড় (1,-1)
(gof)(2)= g[f(2)]= g (3) =4
∴ক্রমিত জোড় (2,4)
(gof)(3)= g[f(3)]= g(4)=2
∴ ক্রমিত জোড় (3,2)
(gof)(4)= g[f(4)]= g(1)= -2
∴ক্রমিত জোড় (4,-2)
∴ ক্রমিত জোড় সমূহের সেট হলও {(1,-1), (2,4), (3,2) (4,-2)}
SN Dey Solution For Class 12 Mapping or Function
6.মনে করো দুটি অপেক্ষক f ও g নিম্নরুপে সংজ্ঞাত ঃ
f = {(1,2),(3,-2),(-1,1)} এবং g= {(2,3),(-2,1),(1,3)} দেখাও যে (gof) এবং (fog) উভয় ই সংজ্ঞাত ।(gof) এবং (fog) উভয়ের ক্রমিত জোড় সমূহের সেট গুলি নির্ণয় করো ।
সমাধান ঃ
f এর ক্ষেত্র = {1,3,-1}
f এর পাল্লা = {2,-2,-1}
g এর ক্ষেত্র = {2,-2,1}
g এর পাল্লা = {3,1}
এক্ষেত্রে f পাল্লা (range) = g এর ক্ষেত্র (domain)
সুতরাং (gof) সংজ্ঞাত ।
আবার g এর পাল্লা (range )= f এর ক্ষেত্রের (domain) উপসেট(subset )
সুতরাং (fog) সংজ্ঞাত ।
এখন gof(1)= g[f(1)]=g(2)=3
∴ ক্রমিত জোড় টি হলও (1,3)
gof(3)=g[f(3)]=g(-2)=1
∴ ক্রমিত জোড় টি হলও (3,1)
gof(-1) = g[f(-1)]= g(1)= 3
∴ ক্রমিত জোড় টি হলও (-1,3)
∴ gof এর ক্রমিত জোড় গুলি হলও { (1,3), (3,1), (-1,3)}
আবার (fog)(2)=f[g(2)]=f(3)=-2
∴ ক্রমিত জোড় টি হলও (2,-2)
fog(-2)=f[g(-2)]= f(1)=2
∴ ক্রমিত জোড় টি হলও (-2,2)
Fog(1)= f[g(1)]= f(3)=-2
∴ ক্রমিত জোড় টি হলও (1,-2)
সুতরাং (fog) এর ক্রমিত জোড় গুলি হলও {(2,-2),(-2,2),(1,-2)}
7.মনে করো f:R → R , g:R → R এবং h:R to R চিত্রণ তিনটি যথাক্রমে f(x)= cosx , g(x)= 2x+1 এবং h(x)= x3-x-6 দ্বারা সংজ্ঞাত । ho(gof) নির্ণয় করো । তারপর [ho(gof)](π/3)- এর মান নির্ণয় করো ।
সমাধানঃ
এক্ষেত্রে f এর পাল্লা = g এর ক্ষেত্র
∴ (gof):R to R সংজ্ঞাত
আবার (gof) এর পাল্লা = h এর ক্ষেত্র
∴ ho(gof):R to R সংজ্ঞাত
f:R to R , g:R to R এবং h:R to R চিত্রণ তিনটি যথাক্রমে f(x)= cosx , g(x)= 2x+1 এবং h(x)= x3-x-6 দ্বারা সংজ্ঞাত
নএখন [ho(gof)](x)
= h[(gof)x]
=h[g{f(x)}]
=h[ g(cosx)]
=h[2cosx+1]
=(2cosx+1)3-2(cosx+1)-6
=8 cos3x+12cos2x+4cosx-6
∴ (ho(gof))(π/3)
= 8cos3 (π/3)+12 cos2 (π/3)+4cox(π/3)-6
=8 (1/8)+12(1/4)+4(1/2)-6
= 1+3+2-6
=6-6
=0
8.মনে করো f:R to R অপেক্ষক নিম্নরুপে সংজ্ঞাত
f(x)= x, যখন x∈Q
= 1-x, যখন x ∉ Q
প্রমান কর fof = IR
সমাধানঃ
f(x)= x, যখন x∈Q
= 1-x, যখন x ∉Q
∴ fof(x)= f(f(x))=f(x)=x , সব x ∈ Q এর জন্য
আবার (fof)(x)
= f(f(x))=f(1-x)
=1-(1-x) [ যেহেতু x∉Q ∴ 1-x ∉ Q ]
=x , for all x ∉Q
অর্থাৎ fof= IR
9.যদি f:R-{7/5} → R-{3/5} অপেক্ষক f(x)= (3x+4)/(5x-7) দ্বারা এবং g:R-{3/5} → R-{7/5} অপেক্ষক g(x)= (7x+4)/(5x-3) দ্বারা সংজ্ঞাত হয় , তবে প্রমান করো যে fog=IA এবং gof=IB যেখানে IA এবং IB যথাক্রমে A=R-{3/5} ও B = R-{7/5} সেটের ওপর identity অপেক্ষক ।
সমাধানঃ
এক্ষেত্রে f এর পাল্লা (range) = g এর ক্ষেত্র (domain)
সুতরাং gof চিত্রণ টি সংজ্ঞাত ।
আবার g এর পাল্লা (range ) = f এর ক্ষেত্র (domain)
সুতরাং fog চিত্রণ টি সংজ্ঞাত ।
এখন
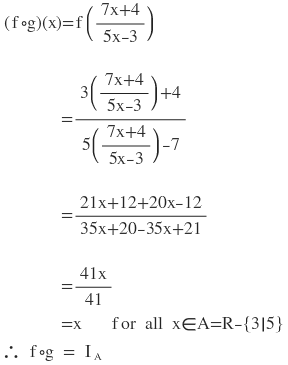
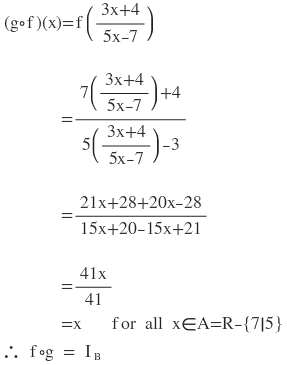
প্রশ্নমালা-2C
অতিসংক্ষিপ্ত উত্তরধর্মীঃ
1. f:A → B একটি এক-এক উপরিচিত্রণ হলে বিপরীত চিত্রণ f-1:B to A –এর সংজ্ঞা দাও ।
সমাধানঃ মনে করো , A ও B -এর কোনোটিই শূন্য সেট নয় এমন f :A to B একটি এক-এক উপরিচিত্রণ । তাহলে যদি একটি চিত্রণ g :B to A ,যা B সেটের প্রত্যেক পদ y –কে A সেটের একটি নির্দিষ্ট পদ x-কে এমনভাবে সংজুক্ত করে যে , f(x) =y , তবে g কে f –এর বিপরীত চিত্রণ বলা হবে । f –এর বিপরীত চিত্রণ f -1 দ্বারা প্রকাশ করা হয় ।
2. মনে করো A ={-2,-1,0,1,2 } এবং f:A → A চিত্রণ নিম্নরূপে সংজ্ঞাতঃ f(-2) = 1 ,f( -1) =-2 ,f(0) = 1 ,f(1) -1 ,f(2) =1
(i) f-1 (-1) , (ii) f -1 (2) ,(iii) f-1 (1) , (iii) f-1 (1) এবং (iv) f-1{-2,-1} ,নির্ণয় করো ।
সমাধানঃ (i) f-1 (-1) = 1 [∵f(1) -1 ]
(ii) f -1 (2) = ∅ [∵ f(x) ≠ 2 ∀ x ∈A]
(iii) f-1 (1) = {2,0,-2} [∵ f(0) = f(2) = f(-2) =1]
(iv) f-1{-2,-1} = {-1,1} [∵ f(-1) =-2 , f(1) = -1 ]
3. মনে করো f:R → R অপেক্ষক f(x) = x2 দ্বারা সংজ্ঞাত ।
(i) f-1 (25) ,(ii) f-1(5 ) এবং f-1(-5) নির্ণয় করো ।
সমাধানঃ (i)f-1 (25) = {x∈R : f(x) =25 } = {x∈R : x2= 25 } = {5 ,-5}
(ii) f -1 (5) = {x ∈ R : f(x) =5 } = {x ∈ R : x2= 5 } = {-√5 ,√5 }
(iii) f-1(-5) = {x ∈ R : f(x) = -5 }= {x ∈ R : x2= -5 } = ∅ [ ∵ x2 ≥ 0 ∀ x ∈
4. মনে করো , A = {a,b,c} এবং B ={p,q,r} ; B সেটে , A সেটের তিনটি এক-এক উপরিচিত্রণ সংজ্ঞাত করো এবং তাদের বিপরীত চিত্রণ তিনটি নির্ণয় করো ।
সমাধানঃ চিত্রণ তিনটি হবে ,
(i) f(a) =p ,f(b) =q ,f(c) = r
(ii) f(a) = p ,f(b) = r ,f(c) =q
(iii) f(a) =q , f(b) =p ,f(c) =r
∴ যে চিত্রণ তিনটি নেওয়া হল তাদের বিপরীত চিত্রণ গুলি হলঃ
(i) f-1(p) =a , f-1 (q) =b , f-1 (r ) = c
(ii) f-1 (p) =a , f-1 (r) = b, f-1 (q) = c
(iii) f-1 (q) =a , f-1 (p) = b , f-1 (r) = c
5. মনে করো , সব জটিল সংখ্যার সেট C এবং f :C → C চিত্রণ f(x) =3x2+16 দ্বারা প্রদত্ত , (i) f-1(1) ,(ii) f-1(11) এবং (iii) f-1(28) নির্ণয় করো ।
সমাধানঃ f(x) =3x2+16
(i) f-1(1) = {x ∈ C : 3x2+16 =1 } ={x ∈ C : x2 = -5 } = {± √(5i2)} = {± i√5 }
(ii) f-1(-11) = {x ∈C : 3x2+16 = -11 } ={x∈C : x2 = -9 } = {± √(9i2)} = {± 3i}
(iii) f-1(28) = {x ∈ C : 3x2+16 = 28 } ={x∈C : x2 = 4} = {± √4} = {± 2}
6. মনে করো, f:R → R অপেক্ষক f(x) = 3x2-14x +10 দ্বারা প্রদত্ত ; (i) f-1(-2) ,(ii) f-1(-4) এবং (iii) f-1( -8) নির্ণয় করো ।
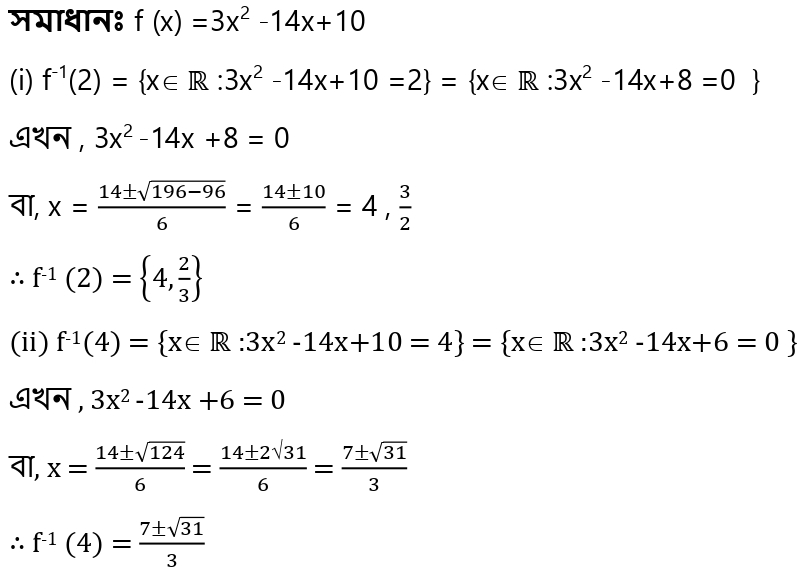
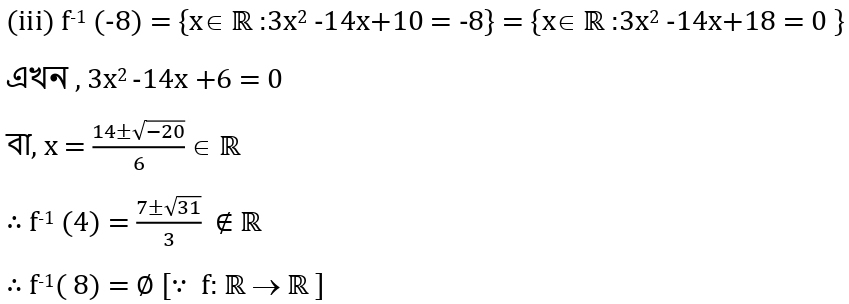
7. মনে করো ,f : R →R চিত্রণ f(x) = x2-2 দ্বারা সংজ্ঞাত । (i) f-1 {-1, 7} ,(ii) f-1{2 ≤ x ≤ 34 }, (iii) f-1 {-5≤ x ≤14 }, (iv) f-1 {-6 ≤ x ≤-2 } (v) f-1 {-∞≤ x ≤ 2 } নির্ণয় করো ।
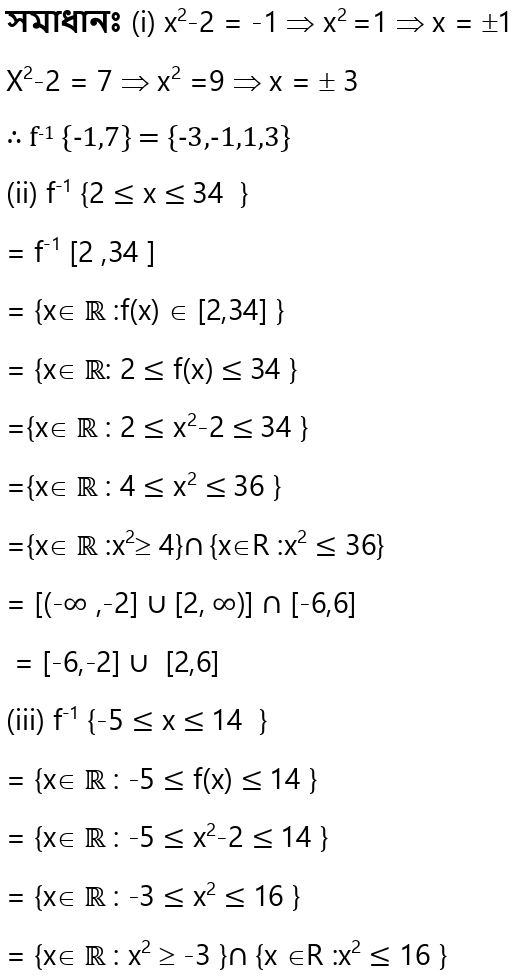
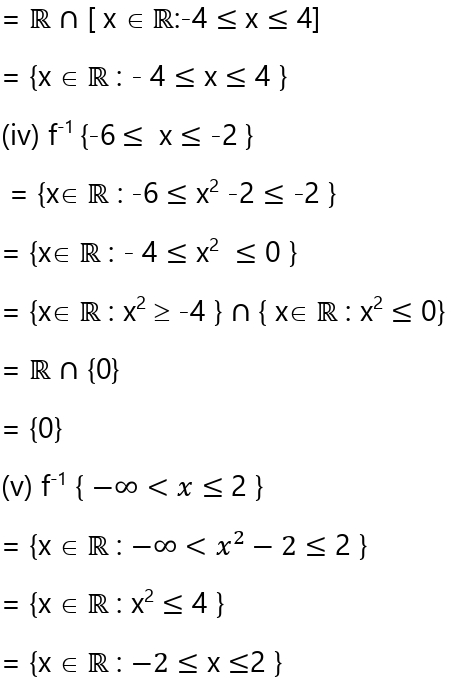
8. মনে করো , সব x ∈ Q –এর জন্য f:Q → Q চিত্রণ f(x) = 4x-5 দ্বারা সংজ্ঞাত । দেখাও যে , f –এর বিপরীত চিত্রণের অস্তিত্ব আছে এবং তারপর f-1 নির্ণয় করো ।
সমাধানঃ ধরা যাক , x1 ,x2 ∈ Q এমন যে ,
x1 ≠ x2
⇒ 4x1 ≠ 4x2
⇒ 4x1-5 ≠ 4x2-5
⇒ f(x1) ≠ f(x2)
∴ f একটি এক –এক চিত্রণ ।
আবার , যেকোনো y ∈ Q (Co-Domain) –এর জন্যে y+5 /4 ∈ Q (Domain)
এবং f [( y+5) /4] = 4 {( y+5) /4} -5 = y
∴ f একটি উপরিচিত্রণ ।
সুতরাং , f –এর বিপরীত চিত্রণের অস্তিত্ব আছে ।
এখন , y = f(x)
⇒ y =4x-5
⇒ x = (y+5) /4
∴ f-1(x)= (x+5) /4,x ∈ Q
সংক্ষিপ্ত উত্তরধর্মীঃ
1. মনে করো , A = {x ∈ R : -1≤ x ≤1} এবং A সেটে ওই একই সেটের দুটি অপেক্ষক f ও g যথাক্রমে f(x) = x2 ও g(x) = x5 দ্বারা সংজ্ঞাত । দেখাও যে , g-1 –এর অস্তিত্ব আছে কিন্তু f-1 –এর অস্তিত্ব নেই ।
সমাধানঃ f(x) = x2 অপেক্ষকের ক্ষেত্রে
-1 , 1 ∈ A এবং -1 ≠1 কিন্তু f(-1) =f(1) = 1
∴ f(x) = x2 চিত্রণটি এক-এক চিত্রণ নয় , সুতরাং চিত্রণটি একটি বাইজেকটিভ চিত্রণ নয় । ∴ f-1 এর অস্তিত্ব নেই ।
g(x) = x5 চিত্রণের ক্ষেত্রে
ধরা যাক , x1 , x2 ∈ A(Domain) এমন যে ,
g(x1) =g(x2)
এখন , g(x1) =g(x2)
⇒ x15 =x25
⇒ x1 = x2 [∵ x1 ,x2 বাস্তব ]
∴ g চিত্রণটি এক –এক চিত্রণ ।
ধরা যাক , y ∈ A (Co-Domain )
এখন , g(x) =y ⇒ x5 = y ⇒ x = y 1/5
আবার , y ∈ A , ∴ -1 ≤ y ≤1 ⇒ -1 ≤ y 1/5 ≤ ⇒ y 1/5 ∈ A
সুতরাং যেকোনো y ∈ A(Co –Domain) – এর জন্য একটি প্রাগবিম্ব
x = y 1/5 ∈ A (Domain) আছে ।
∴ g –একটি উপরিচিত্রণ । সুতরাং , g চিত্রণটি বাইজেকটিভ অর্থাৎ g-1 –এর অস্তিত্ব আছে ।
2. মনে করো , A = R-{3} এবং B = R –{1} ; প্রমাণ করো যে , f:A → B অপেক্ষক , যা f(x) = (x-2) /(x-3) দ্বারা সংজ্ঞাত , একটি এক-এক উপরিচিত্রণ । যে সূত্র দ্বারা f-1 সংজ্ঞাত হয় , তা নির্ণয় করো ।
সমাধানঃ ধরা যাক , a,b ∈ A এমন যে , f(a) =f(b)
এখন , f(a) = f(b)
⇒ (a-2) /(a-3) = (b-2)/(b-3)
⇒ (a-2) (b-3) = (a-3)(b-2)
⇒ ab -2b -3a +6 = ab -3b-2a +6
⇒ a = b
∴ f একটি এক-এক চিত্রণ ।
ধরা যাক , y ∈ B
এখন , f(x) = y
⇒ (x-2) /(x-3) = y
⇒ x = (2-3y) /(1-y) ——(1)
স্পষ্টতই ,
(2-3y) /(1-y) ∈ R –{3} [ ∵ (2-3y) /(1-y) =3 ⇒ 2-3y = 3-3y ⇒ 2 =3 , যা অসম্ভব ]
সুতরাং , যেকোনো y ∈ B –এর জন্য একটি প্রাগবিম্ব x = (2-3y) /(1-y) আছে ।
∴ f একটি উপরিচিত্রণ ।
(1) –এর সাহায্য বলা যায়,
f-1 (y) = (2-3y) /(1-y) ∀ y ∈ B
⇒ f-1(x) = (2-3x) /(1-x) ∀ x ∈ B
3. মনে করো , A ={x : – π /2 ≤ x ≤ π/2 } এবং B = {x: -1≤ x ≤ 1}; দেখাও যে , x ∈A –এর জন্য f :A to B চিত্রণ যা f(x) =sinx দ্বারা সংজ্ঞাত , একটি বাইজেকশন । তারপর , যে সূত্র দ্বারা f-1 সংজ্ঞাত হয় , তা নির্ণয় করো ।
সমাধানঃ ধরা যাক , a ,b ∈ A
∴ – π /2 ≤ a,b ≤ π/2 যেখানে a ≠ b
a ≠ b ⇒ sina ≠ sinb [∵ – π /2 ≤ a,b ≤ π /2 ]
⇒ f(a) ≠ f(b)
∴ f চিত্রণটি একটি এক-এক চিত্রণ ।
ধরা যাক , y ∈ B ∴ -1 ≤ y ≤1 ]
∴ f(x) =y ⇒ sinx =y
⇒ x =sin-1 y [∵ -1 ≤ y ≤ 1] —(i)
এখন , -1 ≤ y ≤ 1 ⇒ – π /2 ≤ sin-1 y ≤ π /2
∴ x = sin-1y ∈ A
সুতরাং যে –কোনো y ∈ B –এর জন্য একটি প্রাগবিম্ব x = sin-1y ∈ A আছে ।
∴ f একটি উপরিচিত্রণ ।
∴ f চিত্রণটি বাইজেকটিভ
(1) থেকে বলা যায়,
f-1 (y) = sin-1 y for all y ∈ B
⇒ f-1(x) =sin-1x for all x ∈ B
4. মনে করো , A = R – {-1/2} , B =R –{1/2}এবং f :A → B অপেক্ষক f(x) = (x+2) / (2x+1)দ্বারা সংজ্ঞাত । প্রমাণ করো যে , f –এর বিপরীতের অস্তিত্ব আছে এবং তারপর f-1 (x) নির্ণয় করো ।
সমাধানঃ ধরা যাক , a ,b ∈ Aএমন যে , f(a) = f(b) ।
f(a) =f(b)
⇒ (a+2) / (2a+1) = (b+2) / (2b+1)
⇒ (a+2) (2b+1) = (b+2) (2a+1)
⇒ 2ab +4b+a+2 = 2ab+4a +b+2
⇒ a=b
∴ f একটি এক-এক চিত্রণ ।
ধরা যাক , y ∈ B
এখন , f(x) = y
⇒ (x+2) /(2x+1) = y
⇒ x = (2-y) / (2y-1) —- (i)
স্পষ্টতই , (2-y) / (2y-1) ∈ R – {-1/2} =A [∵(2-y) / (2y-1)= -1/2 ⇒ 2 =1/2 যা সম্ভব নয় ]
সুতরাং , যেকোনো y ∈ B –এর জন্য একটি প্রাগবিম্ব x = (2-y) / (2y-1) ∈A আছে ।
∴ f একটি উপরিচিত্রণ ।
সুতরাং , f বাইজেকটিভ ⇒ f –এর বিপরীত চিত্রণের অস্তিত্ব আছে ।
(1) থেকে বলা যায় ,
f-1(y) = (2-y) / (2y-1) for all y ∈ B
⇒ f-1(x) = (2-x) / (2x-1) for all x ∈ B
5. মনে করো , f:Q → Q এবং g:Q → Q অপেক্ষক দুটি যথাক্রমে f(x) = 3x এবং g(x) = x+3 দ্বারা সংজ্ঞাত । f এবং g উভয়ের বিপরীত অপেক্ষকের অস্তিত্ব আছে ধরে দেখাও যে ,
(gof) -1 = ( f-1og-1) ।
সমাধান:
(gof)(x) =g(f(x)) =g(3x) =3x+3 ∀ x∈Q
ধরা যাক , y= 3x+3 ⇒ x= (y-3) / 3
∴ (gof)-1 (y) = (y-3) / 3 ∀ y∈Q
⇒ (gof)-1(x) =(x-3) / 3 ∀ x∈Q
স্পষ্টতই ,
g-1 (x) = x-3 ∀ x∈Q
এবং f-1 (x) = x/3 ∀ x∈Q
∴ (f-1 o g-1 ) (x) = f-1(g-1(x))
= f-1(x-3)
=(x-3) / 3 ∀ x∈Q
∴ (gof)-1 = f-1 o g-1
6. মনে করো , সব x∈R –এর জন্য f:R → R চিত্রণ f(x) = x3 – 6 দ্বারা সংজ্ঞাত । দেখাও যে , f চিত্রণটি বাইজেকটিভ । f-1(x) যে সূত্র দ্বারা সংজ্ঞাত হয় , তা নির্ণয় করো ।
সমাধান:
ধরা যাক, x1,x2 ∈R এমন যে , f(x1) = f(x2)
⇒ x13 -6 =x23-6
⇒ x13=x23
⇒ x1=x2 [∵ x1, x2 বাস্তব ]
∴ f চিত্রণটি এক এক ।
ধরা যাক , y∈R ।
এখন , f(x) =y ⇒ x3 -6 =y
⇒ x= ∛(y+6) ……(1)
সুতরাং , যেকোনো y∈ R – এর জন্য একটি প্রাগবিম্ব x= ∛ (y+6) আছে ।
∴ f চিত্রণটি সারজেকটিভ ।
সুতরাং , f চিত্রণটি বাইজেকটিভ ।
(1) থেকে বলা যায় ,
f-1(y) = ∛(y+6) ∀ y∈ R
⇒ f-1(x) = ∛(x+6) ∀ x∈R
7.মনে করো , A ={0,1,2,3} ,B ={1,4,7,10} ,C = {5,11,17,23} f:A → B , g :B → C চিত্রণ দ্বয় f(x) =3x+1 এবং g(x) = 2x+3 দ্বারা সংজ্ঞাত । দেখাও যে , (g of) -1 =f-1 o g-1 ।
সমাধানঃ f = {(x,y):x ∈ A ,এবং y =f(x) =3x+1 }
⇒ f = {(0,1) ,(1,4) ,(2,7) ,(3,10) }
⇒ f-1 = {(1,0) , (4,1) ,(7,2) , (10 ,3) }
এবং g = {{(x,y):x ÎB এবং y =g(x) =2x+3}
g = {(1,5) ,(4,11) ,(7,17) ,(10,23) }
⇒ g-1 = {(5,1) ,(11,4) , (17,7) ,(23,10) }
(gof) -1 এর ক্ষেত্রে ,
gof = {(0,5) ,(1,11) ,(2,17),(3,23)}
⇒ (g of) -1 = {(5,0) , (11,1 ) ,(17,2) ,(23,3) }
f-1 og-1 –এর ক্ষেত্রে ,
f-1og-1 = {(5,0),(11,1) ,(17,2) ,(23,3) }
∴ (gof) -1 = f-1og-1
8. মনে করো ,f : R + → [ -5, ∞) অপেক্ষক f(x) = 9x2 +6x-5 দ্বারা প্রদত্ত । দেখাও যে , f –এর বিপরীত অপেক্ষক আছে তা হল
f-1 (y) = {√(y+6) -1}/3 ।
সমাধানঃ ধরা যাক , a , b ∈ R+ এমন যে , f(a) =f(b) ।
f(a) = f(b)
⇒ 9a2 +6a -5 = 9b2 +6b -5
⇒ 9a2 -9b2 +6a-6b = 0
⇒ 9(a2 –b2) +6(a-b) =0
⇒ 9(a+b)(a-b) +6(a-b) =0
⇒ (a-b) {9(a+b) +6} = 0
⇒ (a-b) (9a+9b+6) = 0
⇒ a =b [ ∵ 9a +9b +6 ≠ 0 ∵ a ,b ∈R+ ]
∴ f একটি এক-এক চিত্রণ ।
ধরা যাক , y ∈ [-5 , ∞) ।

∴ f একটি বাইজেকটিভ অপেক্ষক , সুতরাং f –এর বিপরীত অপেক্ষক আছে ।
(1) থেকে বলা যায়,
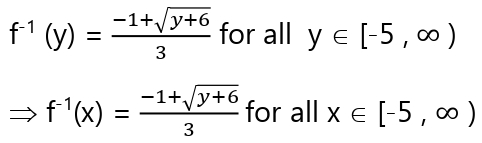
HERE YOU WILL GET FULL S N DEY SOLUTION CLASS-12
CLICK HERE TO GET MORE KNOWLEDGE ON THE FUNCTION