Dighat Somikoron Koshe Dekhi 1.5 Class 10|দ্বিঘাত সমীকরণ দেখি ১.৫|গণিত প্রকাশ সমাধান ক্লাস ১০(টেন) সমাধান |Ganit Prakash Class 10(Ten) Solution|WBBSE Madhyamik class 10(X) Chapter 1 Dighat somikoron 1.5|কষে দেখি 1.5 ক্লাস 10
Dighat Somikoron Koshe Dekhi 1.5 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৫|কষে দেখি 1.5 ক্লাস 10
1.নিচের দ্বিঘাত সমীকরণের বীজদ্বয়ের প্রকৃতি লিখি ঃ-
(i) 2x2+7x+3=0
প্রদত্ত সমীকরণটিকে ax2 +bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a=2 , b= 7 এবং c = 3
∴ নিরূপক = b2-4ac
= (7)2 – 4 (2)(3)
= 49 – 24
= 25 > 0
∴ সমীকরণটির বীজদ্বয় বাস্তব এবং অসমান ।
Dighat Somikoron Koshe Dekhi 1.5 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৫|কষে দেখি 1.5 ক্লাস 10
(ii) 3x2-2√6 x +2=0
প্রদত্ত সমীকরণ টিকে ax2 +bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a= 3 , b = -2√6 , c = 2
∴ নিরূপক = b2-4ac
= (-2√6)2– 4 (3)(2)
= 24-24
= 0
∴ সমীকরণটির বীজদ্বয় বাস্তব ও সমান ।
(iii) 2x2 -7x +9 =0
প্রদত্ত সমীকরণ টিকে ax2 +bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a= 2 , b = -7 , c = 9
∴ নিরূপক = b2-4ac
= (-7)2 – 4 (2)(9)
= 49 – 72
= -23 < 0
∴ সমীকরণটির বীজদ্বয় কাল্পনিক ।
(iv) (2/5)x2 – (2/3)x +1=0
প্রদত্ত সমীকরণ টিকে ax2 +bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a = 2/5 , b = -2/3 এবং c = 1
∴ নিরূপক
= b2-4ac
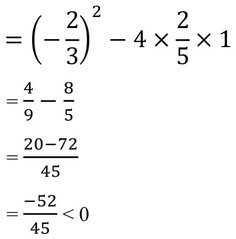
∴ সমীকরণের বীজদ্বয় কাল্পনিক ।
Dighat Somikoron Koshe Dekhi 1.5 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৫|কষে দেখি 1.5 ক্লাস 10
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
2. k এরকোন মান বা মানগুলির জন্য নিচের প্রতিটি দ্বিঘাত সমীকরণের বাস্তব ও সমান বীজ থাকবে হিসাব করে লিখি ।
(i) 49x2 +kx +1 =0
প্রদত্ত সমীকরণ টিকে ax2 +bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a= 49 , b = k , c = 1
যেহেতু সমীকরণটির বীজদ্বয় বাস্তব ও সমান
∴ b2 -4ac =0
বা, (k)2 – 4 (49)(1)=0
বা, k2 -196=0
বা, k2 = 196
বা, k = ±√196
বা, k = ± 14
∴ k এরমান ± 14 ।
(ii) 3x2 – 5x + 2k=0
3x2 -5x + 2k =0
প্রদত্ত সমীকরণ টিকে ax2 +bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a=3 , b = -5 , c = 2k
যেহেতু সমীকরণটির বীজদ্বয় বাস্তব ও সমান
∴ b2 -4ac =0
বা, (-5)2 – 4 (3) (2k) =0
বা, 25 – 24k =0
বা, 24k = 25
বা, k = 25/24
∴ k এর মান 25/24
(iii) 9x2 -24x +k =0
9x2 -24x +k =0
প্রদত্ত সমীকরণ টিকে ax2 +bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a= 9 , b = -24 এবং c = k
যেহেতু সমীকরণটির বীজদ্বয় বাস্তব ও সমান,
∴ b2 -4ac =0
বা, (-24)2 – 4 (9) (k) = 0
বা, 576 -36k = 0
বা, 36k = 576
বা, k = 576 / 36
বা, k = 16
∴ k এর মান 16 ।
(iv) 2x2 +3x +k =0
2x2 +3x +k =0
প্রদত্ত সমীকরণটিকে ax2 +bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a= 2 , b = 3 এবং c = k
যেহেতু সমীকরণটির বীজদ্বয় বাস্তব ও সমান,
∴ b2 -4ac =0
বা, (3)2 – 4(2) (k) =0
বা, 9 – 8k = 0
বা, 8k =9
বা, k = 9/8
∴ k এর মান 9/8
(v) x2 – 2(5+2k)x +3 (7+10k) =0
x2 – 2(5+2k)x +3 (7+10k) =0
প্রদত্ত সমীকরণটিকে ax2 +bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a = 1 , b = -2(5+2k) এবং c = 3(7+10k)
যেহেতু সমীকরণটির বীজদ্বয় বাস্তব ও সমান,
∴ b2 -4ac =0
বা, {-2(5+2k)}2 – 4 (1) {3(7+10k)} =0
বা, 4(5+2k)2 -12(7+10k)=0
বা, 4{(5+2k)2 -3(7+10k)}=0
বা, (5+2k)2 – 3(7+10k) =0 [ উভয়পক্ষে 4 দিয়ে ভাগ করে পাই ]
বা, (5)2 +2 (5)(2k) +(2k)2 – 21- 30k=0
বা, 25 +20k + 4k2 -21 -30k =0
বা, 4k2 -10k +4 =0
বা, 2k2 -5k +2=0
বা, 2k2 -4k –k +2 =0
বা, 2k(k-2) -1(k-2) =0
বা, (k-2)(2k-1)=0
দুটি রাশির গুনফল শূন্য ,
হয় (k-2)=0
বা, k = 2
অথবা, (2k-1)=0
বা, k=1/2
∴ k এর মান 2 এবং 1/2 ।
(vi) (3k+1)x2+2(k+1)x+k=0
সমাধানঃ (3k+1)x2+2(k+1)x+k=0
প্রদত্ত সমীকরণকে ax2+bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a=(3k+1),b=2(k+1) এবং c=k
যেহেতু , দ্বিঘাত সমীকরণের বিজদ্বয় বাস্তব ও সমান,
∴ নিরূপক =0
বা, b2-4ac=0
বা, {2(k+1)}2– 4 ✕ (3k+1) ✕ k =0
বা, 4(k+1)2 -4(3k2+k)=0
বা, 4(k2+2k+1)-12k2-4k=0
বা, 4k2+8k+4-12k2-4k=0
বা, -8k2+4k+4=0
বা, 2k2-k-1=0
বা, 2k2-(2-1)k-1=0
বা, 2k2 -2k+k-1=0
বা, 2k(k-1)+1(k-1)=0
বা, (k-1)(2k+1)=0
দুটি রাশির গুনফল শূন্য
∴ (k-1)=0
বা, k =1
অথবা,
(2k+1)=0
বা, 2k=-1
বা, k = -1/2
∴ k এর মান 1 এবং -1/2
Dighat Somikoron Koshe Dekhi 1.5 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৫|কষে দেখি 1.5 ক্লাস 10
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
3. নিচে প্রদত্ত বীজদ্বয় দ্বারা দ্বিঘাত সমীকরণ গঠন করি ঃ-
(i) 4 ,2
সমাধানঃ
কোনও দ্বিঘাত সমীকরণের দুটি বীজ প্রদত্ত থাকলে সমীকরণ টি হবে
x2 –(বীজদ্বয়ের যোগফল)x + বীজদ্বয়ের গুনফল = 0
∴এক্ষেত্রে দ্বিঘাত সমীকরণটি হবে
= x2– (4+2)x+ 4×2=0
বা, x2 – 6x +8 =0
∴ নির্ণেয় দ্বিঘাত সমীকরণটি হল = x2 – 6x +8 =0 ।
(ii) -4,-3
সমাধানঃ
কোনও দ্বিঘাত সমীকরণের দুটি বীজ প্রদত্ত থাকলে সমীকরণ টি হবে
x2 –(বীজদ্বয়ের যোগফল)x + বীজদ্বয়ের গুনফল = 0
∴এক্ষেত্রে দ্বিঘাত সমীকরণটি হবে
= x2 – {-4+(-3)}x + (-4)(-3) = 0
বা, x2 +7x+12 = 0
∴ নির্ণেয় দ্বিঘাত সমীকরণ টি হল
x2 +7x+12 = 0 ।
(iii) -4, 3
সমাধানঃ
কোনও দ্বিঘাত সমীকরণের দুটি বীজ প্রদত্ত থাকলে সমীকরণ টি হবে
x2 –(বীজদ্বয়ের যোগফল)x + বীজদ্বয়ের গুনফল = 0
∴এক্ষেত্রে দ্বিঘাত সমীকরণ টি হবে
= x2 – (-4+3)x + (-4)(3) =0
বা, x2 +x – 12 = 0
∴ নির্ণেয় দ্বিঘাত সমীকরণটি হল x2 +x – 12 = 0 ।
(iv) 5, -3
সমাধানঃ
কোনও দ্বিঘাত সমীকরণের দুটি বীজ প্রদত্ত থাকলে সমীকরণ টি হবে
x2 –(বীজদ্বয়ের যোগফল)x + বীজদ্বয়ের গুনফল = 0
∴এক্ষেত্রে দ্বিঘাত সমীকরণ টি হবে
x2 – {5+(-3)}x+ 5✕(-3)=0
বা, x2 – (5-3)x+ 5(-3)=0
বা, x2 – 2x -15 = 0
∴ নির্ণেয় দ্বিঘাত সমীকরণটি হবে x2 – 2x -15 = 0
4. m এর মান কত হলে , 4x2 +4(3m-1)x+(m+7)=0 দ্বিঘাত সমীকরণের বীজ দুটি পরস্পর অন্যোন্যক হবে ?
সমাধানঃ
ধরি, দ্বিঘাত সমীকরণটির বীজদ্বয় a এবং 1 / a ।
যেহেতু, বীজদ্বয়ের গুনফল = (ধ্রুবক পদ)/ (x2 এর সহগ)

∴ m এরমান -3 হলে প্রদত্ত সমীকরণটির বীজদ্বয় পরস্পর অন্যোন্যক হবে ।
Dighat Somikoron Koshe Dekhi 1.5 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৫|কষে দেখি 1.5 ক্লাস 10
5. (b-c)x2 +(c-a)x+(a-b)=0 দ্বিঘাত সমীকরণের বীজদ্বয় সমান হলে প্রমান করি যে 2b = a+c ।
সমাধানঃ
প্রদত্ত সমীকরণটিকে Ax2 +Bx+ C = 0 সমীকরণের সাথে তুলনা করে পাই ,
A = (b-c) , B = (c-a) এবং C = (a-b)
যেহেতু প্রদত্ত সমীকরণটির বীজদ্বয় সমান
∴ নিরূপক = B² – 4 AC = 0
বা, (c-a)2–4(b-c)(a-b)= 0
বা, c2 -2ca + a2 – 4ab+ 4 ac + 4b2 -4bc = 0
বা, a2+4b2+c2-4ab -4bc +2ac = 0
বা, a2 + (-2b)2 +c2 + 2(a)(-2b) + 2 (-2b)(c) + 2 a c = 0
বা, {a + (-2b)+ c }2 = 0 [ যেহেতু , (a+b+c)2= a2+b2+c2+2ab+2bc+2ca ]
বা, (a-2b+c)2 = 0
বা, (a-2b+c) =0
বা, a+c = 2b [প্রমানিত ]
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
6. (a2+b2)x2 – 2(ac+bd)x + (c2 +d2) = 0 দ্বিঘাত সমীকরণের বীজদ্বয় সমান হলে প্রমান করি যে a/b = c/d ।
সমাধানঃ
প্রদত্ত সমীকরণটিকে Ax2 +Bx+ C = 0 সমীকরণের সাথে তুলনা করে পাই ,
A = (a2+b2)
B = -2 (ac+bd)
C = (c2 +d2)
যেহেতু সমীকরণের বীজদ্বয় সমান
∴ নিরূপক = B² – 4 AC = 0
বা, {-2(ac+bd)}2 – 4(a2+b2)(c2+d2) = 0
বা, 4(ac+bd)2 – 4 (a2c2+b2c2+a2d2+b2d2) = 0
বা, 4{(ac)2 +2 (ac)(bd) +(bd)2} – 4a2c2-4b2c2-4a2d2-4b2d2 = 0
বা, 4(a2c2 + 2acbd +b2d2 –a2c2 –b2c2-a2d2-b2d2) = 0
বা, {b2c2 -2(bc)(ad) + a2d2 } = 0 [উভয়পক্ষে 4 দ্বারা ভাগ করে পাই ]
বা, (bc – ad)2 =0
বা, (bc – ad) = 0
বা, bc = ad
বা, c/d = a/b
বা , a/b = c/d [ প্রমানিত ]
7. প্রমান করো যে (a2+b2)x2 +2(a+b)x+1 =0 দ্বিঘাত সমীকরণের কোনও বাস্তব বীজ থাকবে না যদি a ≠ b হয় ।
সমাধানঃ
প্রদত্ত সমীকরণটিকে Ax2 +Bx+ C = 0 সমীকরণের সাথে তুলনা করে পাই ,
A = 2(a2+b2)
B = 2(a+b)
C = 1
এখন নিরূপক = B2 -4AC
= {2(a+b)}2 – 4 {2(a2+b2)}
= 4(a2 +2ab+b2)-8a2-8b2
= 4a2+8ab+4b2 -8a2 -8b2
= -4a2+8ab-4b2
=-4(a2 -2ab+b2)
= – 4(a-b)2
এখন {- 4(a-b)2 } রাশিটি সর্বদা ঋণাত্মক কারণ (a-b)2 সর্বদা ধনাত্মক ।
এখন , a = b হলে B2 -4AC = 0 হবে
সেক্ষেত্রে সমীকরণটির বীজদ্বয় বাস্তব ও সমান হবে ।
∴ a ≠ b হলে B2 -4AC < 0 হবে
∴ a ≠ b হলে দ্বিঘাত সমীকরণটির কোনও বাস্তব বীজ থাকবে না [প্রমানিত] ।
Dighat Somikoron Koshe Dekhi 1.5 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৫|কষে দেখি 1.5 ক্লাস 10
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
8. 5×2 +2x -3=0 দ্বিঘাত সমীকরণের দুটি বীজ α এবং β হলে ,(i) α2 + β2 (ii) α3 +β3 (iii) 1/α + 1/β (iv) α2/β + β2/ α এর মান নির্ণয় করো ।
সমাধানঃ
5x2 +2x -3 =0 সমীকরণের দুটি বীজ α ও β ।
∴α + β =-(x এর সহগ)/(x2 এর সহগ)= -2/5 ———(i)
এবং αβ =(ধ্রুবক পদ)/(x2 এর সহগ)= -3/5 ——(ii)
(i) α2 + β2
সমাধানঃ

(ii) α3 + β3
সমাধানঃ

(iii) 1/α + 1/β
সমাধানঃ
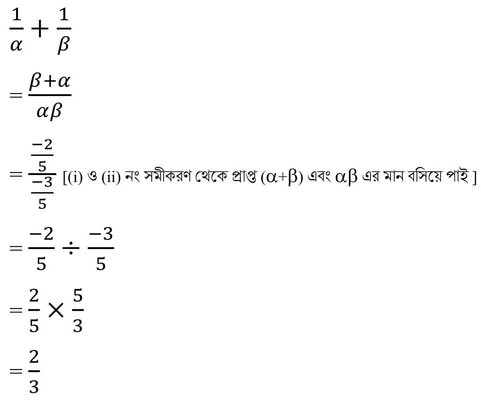
(iv) α2/β + β2/α
সমাধানঃ
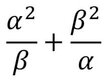

Dighat Somikoron Koshe Dekhi 1.5 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৫|কষে দেখি 1.5 ক্লাস 10
9. ax2+bx+c=0 সমীকরণটির একটি বীজ অপরটির দ্বিগুণ হলে , দেখাই যে 2b2 = 9ac ।
সমাধানঃ
ধরি প্রদত্ত সমীকরণটির একটি বীজ α ।
∴ অন্য বীজটি হবে 2α ।

10. যে সমীকরণের বীজগুলি x2 +px+1 =0 সমীকরণের বীজগুলির অন্যোন্যক , সেই সমীকরণটি গঠন করি ।
সমাধানঃ
ধরি, প্রদত্ত সমীকরণের দুটি বীজ a ও b ।
∴ a+b = -p [যেহেতু, দ্বিঘাত সমীকরণের বীজদ্বয়ের যোগফল = -{(x-এর সহগ)/x2 এর সহগ} ]
এবং ab = 1 [যেহেতু, দ্বিঘাত সমীকরণের বীজদ্বয়ের গুনফল = ধ্রুবক পদ /x2 এর সহগ ]
যে সমীকরণটি তৈরি করতে বলা হয়েছে তার বীজদ্বয় হবে প্রদত্ত সমীকরনের বীজদ্বয়ের অন্যোন্যক অর্থাৎ নতুন সমীকরণের বীজদ্বয় হল 1/a এবং 1/b ।
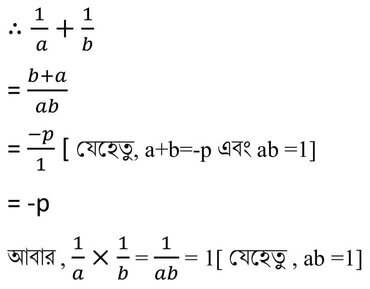
∴ নির্ণেয় সমীকরণটি হবে
= x2-( বীজদ্বয়ের যোগফল) x+(বীজদ্বয়ের গুনফল)=0
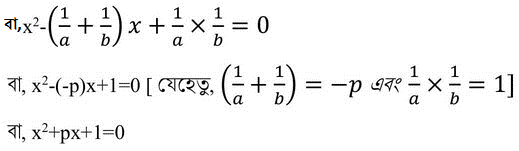
এই সমীকরণটি হল নির্ণেয় সমীকরণ যার বীজদ্বয়, প্রদত্ত সমীকরণের বীজদ্বয়ের অন্যোন্যক ।
Dighat Somikoron Koshe Dekhi 1.5 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৫|কষে দেখি 1.5 ক্লাস 10
11. x2+x+1 =0 সমীকরণের বীজগুলির বর্গ যে সমীকরনের বীজ ,সেই সমীকরণটি নির্ণয় কর ।
সমাধানঃ ধরি, x2+x+1 =0 সমীকরনের বীজগুলি হল a এবং b. আমাদের যে সমীকরণটি নির্ণয় করতে হবে তার বীজগুলি প্রদত্ত সমীকরণের বীজগুলির বর্গ হবে অর্থাৎ a2 এবং b2 বীজ বিশিষ্ট দ্বিঘাতসমীকরণ নির্ণয় করতে হবে ।
x2+x+1 =0 সমীকরনের বীজগুলি হল a এবং b
∴ a+b = -1 এবং ab = 1
এখন , a2+b2
= (a+b)2-2ab
= (-1)2-2(1) [∵ a+b = -1 এবং ab = 1]
= 1-2
=-1
এবং a2b2 = (ab)2 =(1)2 =1[∵ab = 1]
নির্ণেয় সমীকরণটি হল ,
x2-(a2+b2)x+a2b2=0
= x2-(-1)x+1=0
= x2+x+1
∴ x2+x+1 এই সমীকরণটি হল সেই সমীকরণ যার বীজগুলি প্রদত্ত দ্বিঘাত সমীকরণের বীজগুলির বর্গ ।
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
12. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q)
(i) x2-6x+2=0 সমীকরণের বীজদ্বয়ের সমস্টি
(a) 2
(b) -2
(c) 6
(d) -6
Ans:(c) 6
সমাধানঃ x2-6x+2=0 সমীকরণের বীজদ্বয়ের সমস্টি = -(x এর সহগ)/ (x2 এর সহগ)= -(-6)/1= 6
(ii) x2-3x+k=10 সমীকরণের বীজদ্বয়ের গুনফল -2 হলে, k এর মান
(a) -2
(b) -8
(c) 8
(d) 12
Ans:(c) 8
সমাধানঃ
x2-3x+k=10
বা, x2-3x+(k-10)=0
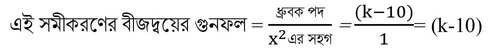
∴ (k-10) = -2 [ যেহেতু প্রদত্ত সমীকরণের বীজদ্বয়ের গুনফল -2 প্রদত্ত ]
বা, k=10-2
বা, k =8
Dighat Somikoron Koshe Dekhi 1.5 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৫|কষে দেখি 1.5 ক্লাস 10
(iii) ax2+bx+c=0 (a≠0) সমীকরণের বীজদ্বয় বাস্তব ও অসমান হলে ,b2 -4ac হবে ,
(a) > 0
(b) =0
(c) <0
(d) কোনোটিই নয়
Ans:(a) > 0
(iv) ax2+bx+c=0 (a≠0) সমীকরণের বীজদ্বয় সমান হলে,
(a) c=- b/2a
(b) c= b/2a
(c) c= -b2/4a
(d) c=b2/4a
Ans:(d) c=b2/4a
সমাধানঃ ax2+bx+c=0 (a≠0) সমীকরণের বীজদ্বয় সমান হলে, নিরূপক শূন্য হয় অর্থাৎ,
b2-4ac =0
বা, b2 = 4ac
বা, c = b2/4a

Dighat Somikoron Koshe Dekhi 1.5 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৫|কষে দেখি 1.5 ক্লাস 10
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখিঃ
(i) x2+x+1 সমীকরণের বীজগুলি বাস্তব ।
উত্তরঃ বিবৃতিটি মিথ্যা ।
x2+x+1=0 সমীকরণটিকে ax2+bx+c=0 সমীকরণের সাথে তুলনা করে পাই , a=1,b=1 এবং c =1
নিরূপক = b2-4ac = (1)2-4(1)(1)=1-4=-3<0
সুতরাং প্রদত্ত দ্বিঘাত সমীকরণের বীজগুলি কাল্পনিক ।
∴ বিবৃতিটি মিথ্যা
(ii) x2-x+2=0 সমীকরণের বীজগুলি বাস্তব নয় ।
উত্তরঃবিবৃতিটি সত্য ।
x2-x+2=0 সমীকরণটিকে ax2+bx+c=0 সমীকরণের সাথে তুলনা করে পাই , a=1,b=-1 এবং c =2
নিরূপক = b2-4ac = (-1)2-4(1)(2)=1-8=-7<0
সুতরাং প্রদত্ত দ্বিঘাত সমীকরণের বীজগুলি কাল্পনিক ।
∴ বিবৃতিটি সত্য ।
Dighat Somikoron Koshe Dekhi 1.5 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৫|কষে দেখি 1.5 ক্লাস 10
(C) শূন্যস্থান পূরণ করিঃ
(i) 7x2-12x+18=0 সমীকরণের বীজদ্বয়ের সমষ্টি এবং গুনফলের অনুপাত _________ ।
উত্তরঃ 2:3
সমাধানঃ প্রদত্ত দ্বিঘাত সমীকরণটি হল 7×2-12x+18=0

Dighat Somikoron Koshe Dekhi 1.5 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৫|কষে দেখি 1.5 ক্লাস 10
(ii) ax2+bx+c=0 (a≠0) সমীকরণের বীজদ্বয় পরস্পর অন্যোন্যক হলে, C= ________
উত্তরঃ a
সমাধানঃ

(iii) ax2+bx+c=0 (a≠0) সমীকরণের বীজদ্বয় পরস্পর অন্যোন্যক এবং বিপরীত চিহ্নযুক্ত হলে , a+c= _______
উত্তরঃ 0
সমাধানঃ ধরি, ax2+bx+c=0 দ্বিঘাত সমীকরণটির একটি বীজ a, ∴ অন্য বীজটি হবে -1/a

মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
13. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন(S.A)
(i) একটি দ্বিঘাত সমীকরণের বীজদ্বয়ের সমষ্টি 14 এবং গুনফল 24 হলে,দ্বিঘাত সমীকরণটি লিখি ।
সমাধানঃ দ্বিঘাত সমীকরণের বীজদ্বয়ের সমষ্টি 14 এবং গুনফল 24
দ্বিঘাত সমীকরণটি হবে
x2 -(বীজদ্বয়ের যোগফল)x+(বীজদ্বয়ের গুনফল)=0
বা, x2-14x+24=0
∴ নির্ণেয় দ্বিঘাত সমীকরণটি হল x2-14x+24=0
(ii) kx2+2x+3k=0 (k≠0) সমীকরণের বীজদ্বয়ের সমষ্টি এবং গুনফল সমান হলে, k এর মান লিখি ।
সমাধানঃ kx2+2x+3k=0 সমীকরণের বীজদ্বয়ের সমষ্টি =-(x এর সহগ)/(x2 এর সহগ)= -2/k
kx2+2x+3k=0 সমীকরণের বীজদ্বয়ের গুনফল = (x এর সহগ) /(x2 এর সহগ) =3k/k =3
kx2+2x+3k=0 (k≠0) সমীকরণের বীজদ্বয়ের সমষ্টি এবং গুনফল সমান
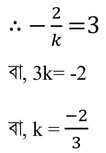
∴ k এর মান -2/3
(iii) x2-22x+105=0 সমীকরণের বীজদ্বয় α ও β হলে, (α-β) এর মান লিখি ।
সমাধানঃ
x2-22x+105=0 সমীকরণের বীজদ্বয় α ও β


মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
(iv) x2-x=k(2x-1) সমীকরণের বীজদ্বয়ের সমষ্টি শূন্য হলে, k এর মান লিখি ।
সমাধানঃ প্রদত্ত দ্বিঘাত সমীকরণটি হল
x2-x=k(2x-1)
বা, x2-x-2kx+k=0
বা, x2-(1+2k)x+k=0
x2-(1+2k)x+k=0, এই সমীকরণের বীজদ্বয়ের সমষ্টি
= -(x এর সহগ)/(x2 এর সহগ)
= -{-(1+2k)}/1
=(1+2k)
শর্তানুসারে ,
(1+2k)=0
বা, 2k=-1
বা, k = -1/2 [উত্তর]
(v) x2+bx+12=0 এবং x2+bx+q =0 সমীকরণদ্বয়ের একটি বীজ 2 হলে,q এর মান হিসাব করে লিখি ।
সমাধানঃ
যেহেতু x2+bx+12=0 সমীকরণের একটি বীজ 2
∴ 2 , সমীকরণটিকে সিদ্ধ করবে
∴ (2)2+2b+12=0
বা, 4+2b+12=0
বা, 2b+16=0
বা, b = -16/2
বা, b = -8 —(i)
আবার , x2+bx+q =0 সমীকরণটির একটি বীজ 2
∴ 2, x2+bx+q =0 সমীকরণটিকে সিদ্ধ করবে ।
∴ (2)2+2b+q=0
বা, 4+2b+q=0
বা, 4+2(-8)+q=0 [(i) নং সমীকরণ থেকে প্রাপ্ত b এর মান বসিয়ে পাই ]
বা, 4-16+q=0
বা, q-12=0
বা, q = 12 [ উত্তর ]
আরও দেখুনঃ
It is good. Keep going
Obviously great 💯 link for our class 10 students
Ami test a ai link follow kora 637 /700
Payachi