Dighat Somikoron Koshe Dekhi 1.1 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.১|WBBSE Madhyamik Class 10(Ten)(X) Dighat Somikoron Koshe Dekhi 1.1|Madhyamik Math Solution In Bengali|WBBSE Class 10 Math Solution Of Chapter 1 Exercise 1.1| মাধ্যমিক গণিত প্রকাশ সমাধান| দ্বিঘাত সমীকরণ সমাধান ক্লাস ১০(টেন)
Dighat Somikoron Koshe Dekhi 1.1 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.১|কষে দেখি 1.1 ক্লাস 10
1.নিচের বহুপদী সংখ্যামালা গুলির মধ্যে কোনটি/কোনগুলি দ্বিঘাত বহুপদী সংখ্যা মালা বুঝে লিখি ।
(i) x2-7x+2
সমাধানঃ
এটি একটি দ্বিঘাত বহুপদী সংখ্যামালা কারণ এক্ষেত্রে বহুপদী সংখ্যামালার x এর সর্বোচ্চ ঘাত 2 ।
(ii) 7x5-x(x+2)
সমাধানঃ
7x5-x(x+2)
=7x5-x2-2x
এটি একটি বহুপদী সংখ্যামালা হলেও দ্বিঘাত বহুপদী সংখ্যামালা নয় কারণ এক্ষেত্রে x এর সর্বোচ্চ ঘাত 5
(iii) 2x(x+5)+1
সমাধানঃ
2x(x+5)+1
=2x2+10x+1
এটি একটি দ্বিঘাত বহুপদী সংখ্যামালা কারণ এক্ষেত্রে বহুপদী সংখ্যামালার x এর সর্বোচ্চ ঘাত 2 ।
(iv) 2x-1
সমাধানঃ
এটি দ্বিঘাত বহুপদী সংখ্যামালা নয় কারণ এক্ষেত্রে x এর সর্বোচ্চ ঘাত 2 নয় ।
2.নীচের সমীকরণগুলির কোনটি ax²+bx+c=0,যেখানে a,b,c বাস্তবসংখ্যা এবং a≠0 আকারে লেখা যায় তা লিখি।
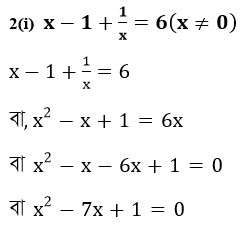
∴ প্রদত্ত সমীকরণটিকে ax2+bx+c আকারে প্রকাশ করা গেল ।
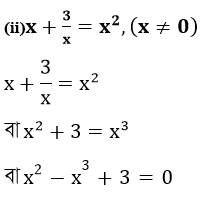
∴ প্রদত্ত সমীকরণটিকে ax2+bx+c আকারে প্রকাশ করা যায় না ।
(iii) x2-6√x+2=0
x2-6√x+2=0
∴ প্রদত্ত সমীকরণটিকে ax2+bx+c আকারে প্রকাশ করা যায় না ।
(iv) (x-2)2 = x2-4x+4
(x-2)2 = x2-4x+4
বা, x2-4x+4 = x2-4x+4
∴ প্রদত্ত সমীকরণটিকে ax2+bx+c আকারে প্রকাশ করা যায় না কারণ এটি একটি অভেদ ।
3. x6-x3-2=0 সমীকরণটি চলের কোন ঘাতের সাপেক্ষে একটি দ্বিঘাত সমীকরণ তা নির্ণয় করি।
সমাধানঃ
x6-x3-2=0
বা, (x3)2-x3-2=0
∴ প্রদত্ত সমীকরণটিকে ax2+bx+c আকারে প্রকাশ করা গেল।
∴প্রদত্ত সমীকরণ টি x3 এর সাপেক্ষে একটি দ্বিঘাত সমীকরণ ।
4(i) (a-2)2+3x+5=0 সমীকরণটি a এর কোন মানের জন্য দ্বিঘাত সমীকরণ হবেনা তা নির্ণয় করি ।
সমাধানঃ প্রদত্ত সমীকরণ টি দ্বিঘাত সমীকরণ হবেনা যদি a-2= 0 হয়
∴ a=2 হলে প্রদত্ত সমীকরণটি দ্বিঘাত সমীকরণ হবে না ।
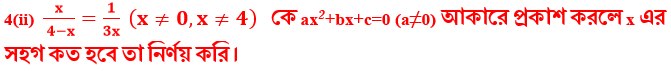

(iii) 3x2+7x+23 = (x+4)(x+3)+2- কে ax2+bx+c =0 (a≠0) দ্বিঘাত সমীকরনের আকারে প্রকাশ করি ।
সমাধানঃ
3x2+7x+23 = (x+4)(x+3)+2
বা, 3x2+7x+23=x2+4x+3x+12+2
বা, 3x2+7x+23=x2+7x+14
বা, 3x2-x2+7x-7x+23-14=0
বা, 2x2+9=0
বা, 2x2+0x+9=0
∴ প্রদত্ত সমীকরণটিকে ax2+bx+c আকারে প্রকাশ করা গেল যেখানে a≠0 ।
(iv) (x+2)3=x(x2-1) -কে ax2+bx+c=0,(a≠0) দ্বিঘাত সমীকরনের আকারে প্রকাশ করি এবং x2,x ও x0 এর সহগ লিখি।
সমাধানঃ
(x+2)3=x(x2-1)
বা, x3+3x2(2)+3(x)(2)2+(2)3 =x3-x
বা, x3+6x2+12x+8=x3-x
বা, 6x2+13x+8=0
∴ প্রদত্ত সমীকরণটিকে ax2+bx+c আকারে প্রকাশ করা গেল যেখানে a≠0 এবং x² এর সহগ 6 , x এর সহগ 13 এবং x0 এর সহগ 8 ।
আরও দেখুনঃ মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধান
5. নিচের বিবৃতি গুলি থেকে একচল বিশিষ্ট দ্বিঘাত সমীকরণ গঠন করি ।
(i) 42 কে দুটি অংশে বিভক্ত করো যাতে একটি অংশ অপর অংশের বর্গের সমান হয়।
সমাধানঃ
ধরি , একটি অংশ x
∴ অপর অংশ (42-x)
শর্তানুসারে,
x2=(42-x)
বা, x²+x-42=0
∴ x²+x-42=0 হল নির্ণেয় দ্বিঘাত সমীকরণ ।
(ii) দুটি ক্রমিক ধনাত্মক অযুগ্ম সংখ্যার গুনফল 143
সমাধান ঃ ধরি একটি সংখ্যা x
∴ অপর সংখ্যাটি হবে (x+2) [ যেহেতু ক্রমিক ধনাত্মক অযুগ্ম সংখ্যা ]
শর্তানুসারে,
X(x+2)=143
বা, x²+2x-143=0
∴ x²+2x-143=0 হল নির্ণেয় দ্বিঘাত সমীকরণ ।
(iii) দুটি ক্রমিক সংখ্যার বর্গের সমষ্টি 313 ।
সমাধানঃ
ধরি , একটি সংখ্যা x
∴ অপর সংখ্যা (x+1)
শর্তানুসারে,
x2+(x+1)2 =313
বা,x²+x²+2x+1=313
বা, 2x²+2x+1=313
বা, 2x²+2x+1-313=0
বা 2x²+2x-312=0
বা, x²+x-156=0 [ উভয়পক্ষে 2 দ্বারা ভাগ করে পাই ]
∴ x²+x-156=0,হল নির্ণেয় দ্বিঘাত সমীকরণ ।
6. নিচের বিবৃতি গুলি থেকে একচল বিশিষ্ট দ্বিঘাত সমীকরণ গঠন করি ।
(i) একটি আয়তকার ক্ষেত্রের কর্ণের দৈর্ঘ্য 15 মিটার এবং তার দৈর্ঘ্য প্রস্থ অপেক্ষা 3মিটার বেশি ।
সমাধানঃ
ধরি , আয়তক্ষেত্রের প্রস্থ x মিটার
∴ আয়তক্ষেত্রের দৈর্ঘ্য (x+3) মিটার
আয়তক্ষেত্রের কর্ণের দৈর্ঘ্য =√(দৈর্ঘ্য²+প্রস্থ²)
শর্তানুসারে ,
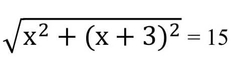
উভয়পক্ষ কে বর্গ করে পাই,
x²+(x+3)²=225
বা, x²+x²+2(x)3+(3)²=225
বা, 2x²+6x+9=225
বা, 2x²+6x+9-225=0
বা, 2x²+6x-216=0
বা, x²+3x-108=0 [উভয়পক্ষে 2 দ্বারা ভাগ করে পাই ]
∴ নির্ণেয় দ্বিঘাত সমীকরণটি হল x²+3x-108=0
(ii) এক ব্যাক্তি 80 টাকায়ে কয়েক কিগ্রা চিনি ক্রয় করলেন। যদি ওই টাকায়ে তিনি আর ও 4 কিগ্রা চিনি বেশি পেতেন তবে তার কিগ্রা প্রতি চিনির দাম 1 টাকা কম হত ।
ধরি , প্রতি কিগ্রা চিনির মূল্য x টাকা
∴ 80 টাকায় পাওয়া যাবে 80/x কিগ্রা চিনি
এখন প্রতি কিগ্রা চিনির দাম (x-1)টাকা হলে, 80 টাকায় পাওয়া যাবে 80/(x-1) কিগ্রা চিনি
শর্তানুসারে,
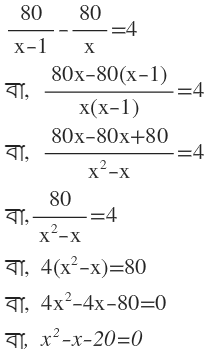
∴ নির্ণেয় দ্বিঘাত সমীকরণটি হল x²-x-20 =0
আরও দেখুনঃ মাধ্যমিকের সকল বিষয়ের মক টেস্ট
(iii) দুটি স্টেশন এর মধ্যে দূরত্ব 300 km ।একটি ট্রেন প্রথম স্টেশন থেকে সমবেগে দ্বিতীয় স্টেশন এ গেল । ট্রেন টির গতিবেগ ঘণ্টায়ে 5km বেশি হলে ট্রেন টির দ্বিতীয় স্টেশন এ যেতে 2 ঘণ্টা সময় কম লাগত ।
সমাধানঃ
ধরি , ট্রেন টির গতিবেগ xকিমি/ঘন্টা
∴ 300 কিমি যেতে ট্রেনটির সময় লাগবে 300/x ঘন্টা [ যেহেতু , সময় = দূরত্ব /গতিবেগ]
ট্রেনটির গতিবেগ (x+5) কিমি প্রতি ঘণ্টা হলে, 300 কিমি যেতে সময় লাগবে 300/(x+5) ঘণ্টা [ যেহেতু , সময় = দূরত্ব /গতিবেগ]।
শর্তানুসারে ,

∴ নির্ণেয় দ্বিঘাত সমীকরণটি হল x²+5x-750=0
(iv) একজন ঘড়ি বিক্রেতা একটি ঘড়ি ক্রয় করে 336 টাকায়ে বিক্রি করলেন ।তিনি যত টাকায়ে ঘড়ি টি ক্রয় করেছিলেন শতকরা তত টাকা তার লাভ হল ।
ধরি , ঘড়িটি তিনি x টাকায়ে ক্রয় করেছিলেন ।
এবং ঘড়িটি বিক্রি করেছেন 336 টাকায়ে
∴ লাভ= ক্রয়মূল্য – বিক্রয় মূল্য =(336-x) টাকা
∴ শতকরা লাভ= (লাভ/ক্রয় মূল্য)×100=(336-x)/x × 100 %
শর্তানুসারে ,
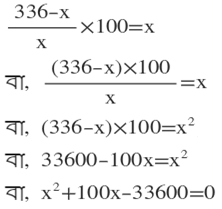
∴ নির্ণেয় দ্বিঘাত সমীকরণটি হল x²+100x-33600=0
Dighat Somikoron Koshe Dekhi 1.1 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.১
(v) স্রোতের বেগ ঘণ্টায়ে 2km হলে রতন মাঝি স্রোতের অনুকুলে 21km গিয়ে ওই দূরত্ব ফিরে আস্তে 10 ঘণ্টা সময় লাগে ।
সমাধানঃ
ধরি, নৌকার বেগ x কিমি /ঘণ্টা
∴স্রোতের অনুকুলে নৌকার বেগ = (x+2) কিমি/ ঘণ্টা
এবং স্রোতের প্রতিকুলে নৌকার বেগ = (x-2) কিমি/ ঘণ্টা
সময় = দুরত্ব/গতিবেগ
∴ স্রোতের অনুকূলে 21 কিমি. যেতে সময় লাগে 21/(x+2) ঘণ্টা এবং স্রোতের প্রতিকূলে 21 কিমি. ফিরে আসতে সময় লাগে 21/(x-2) ঘণ্টা ।
শর্তানুসারে,
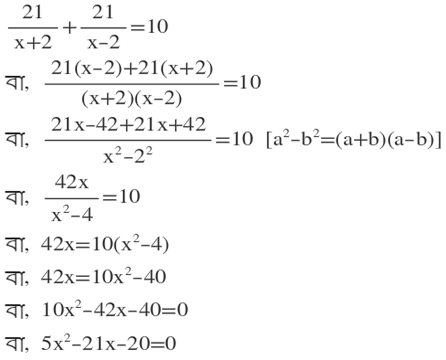
∴ নির্ণেয় দ্বিঘাত সমীকরণটি হল 5x²-21x-20=0
আরও দেখুনঃ মাধ্যমিকের সকল বিষয়ের মক টেস্ট
6(vi) আমাদের বারির বাগান পরিষ্কার করতে মহিম অপেহ্মা মজিদের 3 ঘণ্টা বেশি সময় লাগে । তারা উভয় একসঙ্গে কাজটি 2 ঘণ্টায়ে শেষ করতে পারে ।
সমাধানঃ
ধরি, মহিমের বাগান পরিষ্কার করতে সময় লাগে x ঘণ্টা
∴ মজিদের সময় লাগে (x+3) ঘণ্টা
আরও ধরাযাক মোট কাজের পরিমাণ 1 অংশ ।
∴মহিম x ঘণ্টায়ে কাজ করে 1 অংশ
∴ মহিম 1 ঘণ্টায়ে কাজ করে 1/x অংশ
মজিদ (x+3) ঘণ্টায়ে কাজ করে 1 অংশ
∴ মজিদ 1 ঘণ্টায়ে কাজ করে 1/(x+3) অংশ

শর্তানুসারে,
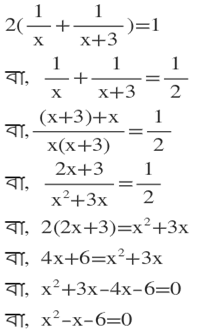
∴ নির্ণেয় দ্বিঘাত সমীকরণটি হল x²-x-6=0
(vii) দুই অঙ্ক বিশিষ্ট একটি সংখ্যার একক স্থানীয় অঙ্ক টি দশক স্থানীয় অঙ্ক অপেহ্মা 6 বেশি এবং অঙ্ক দ্বয়ের গুনফল সংখ্যাটি থেকে 12 কম ।
সমাধানঃ
ধরি দুই অঙ্ক বিশিষ্ট সংখ্যার দশক স্থানীয় অঙ্ক x
∴ একক স্থানীয় অঙ্ক হবে (x+6)
∴ দুই অঙ্ক বিশিষ্ট সংখ্যাটি হল 10x+(x+6)=11x+6
শর্তানুসারে ,
x(x+6)=(11x+6)–12
বা, x²+6x=11x-6
বা, x²+6x-11x+6=0
বা, x²-5x+6=0
∴ নির্ণেয় দ্বিঘাত সমীকরণটি হল x²-5x+6=0
6(viii) 45 মিটার দীর্ঘ ও 40 মিটার প্রসস্থ একটি আয়তক্ষেত্রাকার খেলার মাঠের বাইরের চারপাশে সমান চওড়া একটি রাস্তা আছে এবং ওই রাস্তার ক্ষেত্রফল 450 বর্গ মিটার ।
সমাধান ঃ
ধরি রাস্তাটি x মিটার চওড়া
∴ রাস্তা সহ আয়তক্ষেত্রের দৈর্ঘ্য (45+2x) মিটার
এবং রাস্তা সহ আয়তক্ষেত্রের প্রস্থ (40+2x) মিটার
শর্তানুসারে,
(45+2x)×(40+2x)- (45×40)= 450
বা, 1800+90x+80x+4x² -1800=450
বা, 4x²+170x-450=0
বা, 2x²+85x-225=0
∴ নির্ণেয় দ্বিঘাত সমীকরণটি হল 2x²+85x-225=0 ।
আরও দেখুনঃ মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধান
আরও দেখুনঃ মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধান
আরও দেখুনঃ মাধ্যমিকের সকল বিষয়ের মক টেস্ট
আরও দেখুনঃ WBBSE OFFICIAL SITE
I love you content… Very helpful for every class-x students …. Thank you for this team #ANUSHILAN.com
Thank you very much this is so helpful for revising math
Khub sundar
It’s really good 😊
Tnx anushilani.com ☺️✨💜
Khub valo very good
খুব ভালো লাগলো। It’s very much fruitful for the underprivileged students who don’t have capacity to take tuition privately. It’s a great social work also. This effort is excellent .
Thank you.
nic e
Thanks For This Help. Lots Of Love From Me. It helped me a lot.
Very helpfull website for class X students 😍😍 Thanks anushilan.com team ❤️❤️
Really it’s too good, I am just completed my 9 class exam and I have study in December for next year. It’s help me a lot 😊.
Thank you This is very helpful 😊😊
When I can’t solve any solution I also need this page anushilan.com . I am using this page from class 6 now I am studying in class X 😌😌
So nice😄😄
Well done 👍