If (x+1/x)=3 then find (x^5+1/x^5)
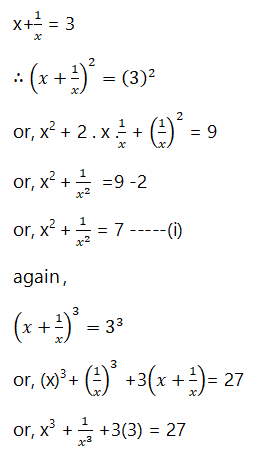
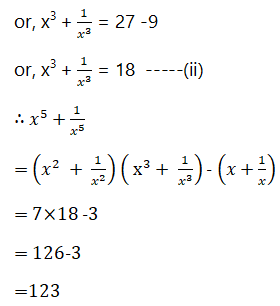
Ans: 123
(x+1/x)= 3
∴ (x+1/x)^2 = 3^2
or, (x+1/x)^2 = 9
or, x^2 + 2.x.1/x + 1/x^2 = 9
or, x^2+1/x^2 +2 = 9
or, x^2+1/x^2 = 9-2
or, x^2+1/x^2=7 —-(i)
again,
(x+1/x)^3= 3^3
or, (x+1/x)^3 = 27
or, x^3+1/x^3+3. x. 1/x. (x+1/x) = 27
or, x^3 +1/x^3 + 3 (x+1/x) = 27
or, x^3 +1/x^3 +3(3) = 27
or, x^3+1/x^3= 27-9
or, x^3+1/x^3 = 18 —–(ii)
∴ (x^5+1/x^5)
= (x^2+1/x^2) (x^3+1/x^3) – (x^3 /x^2 + x^2 /x^3)
= (x^2+1/x^2) (x^3+1/x^3) – (x+1/x)
= 7 × 18 – 3
= 126 -3
=123 (Answer)