Madhyamik 2019 Math Question Solution|Madhyamik 2019 Math Question Paper Solved || Madhyamik 2019 Math Question Answer || মাধ্যমিক ২০১৯ গণিত প্রশ্নের সমাধান || মাধ্যমিক ২০১৯ অঙ্ক প্রশ্নের উত্তর
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধান
Madhyamik 2019 Math Question Solution|Madhyamik 2019 Math Question Paper Solved|Madhyamik 2019 Math Question Answer|মাধ্যমিক ২০১৯ গণিত প্রশ্নের সমাধান।
1.নিম্নলিখিত প্রশ্ন গুলির প্রতিটি ক্ষেত্রে সঠিক উত্তর নির্বাচন করঃ
(i) কোনো অংশীদারি ব্যাবসায় দুই বন্ধুর প্রাপ্ত লভ্যাংশের অনুপাত 1/2 : 1/3 হলে , তাঁদের মূলধনের অনুপাত-
(a) 2:3
(b) 3:2
(c) 1:1
(d) 5:3
Ans: (b) 3:2
সমাধানঃ আমরা জানি কোনো অংশীদারি ব্যাবসায় মূলধনের অনুপাত এবং লভ্যাংশের অনুপাত সমান হয় ।
∴ এক্ষেত্রে মূলধনের অনুপাত হবে
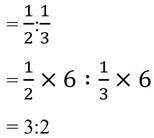
(ii) যদি p+q = √13 এবং p-q = √5 হয় , তাহলে pq এর মান —
(a) 2
(b) 18
(c) 9
(d) 8
Ans: (a) 2
সমাধানঃ
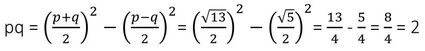
(iii) কোনো বৃত্তের কেন্দ্র O এবং ব্যাস AB । ABCD বৃত্তস্থ চতুর্ভুজ । ∠ABC =65° , ∠DAC=40°হলে ∠BCD এর মান—
(a) 75°
(b) 105°
(c ) 115°
(d) 80°
Ans: (c ) 115°
সমাধানঃ
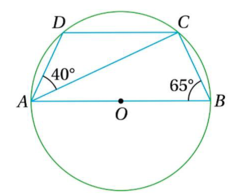
∠ACB অর্ধ বৃত্তস্থ কোণ
∴ ∠ACB = 90°
∴ ∠BAC = 180°-(∠ACB+∠ABC)=180°-(90°+65°)=180°-155°= 25°
∴ ∠DAB = ∠DAC+∠BAC = 40°+25°=65°
আমরা জানি বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক
∴ ∠DAB+∠BCD =180°
বা, 65° +∠BCD = 180°
বা, ∠BCD = 180°-65°
বা, ∠BCD = 115°
(iv) tana+cota =2 হলে, (tan13a +cot13a ) –এর মান
(a) 13
(b) 2
(c ) 1
(d) 0
Ans: (c ) 2
সমাধানঃ tana+cota =2
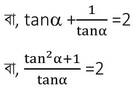
বা, tan2α +1 = 2tanα
বা, tan2α -2tanα +1 =0
বা, (tanα-1)2 =0
বা, (tanα-1) =0
বা, tanα =1
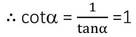
∴ (tan13α +cot13α)
= (1)13 +(1)13
= 1+1
= 2 [উত্তর]
(v) 2√6 সেমি বাহু বিশিষ্ট দুটি ঘনক পাশাপাশি রাখলে উৎপন্ন আয়তঘনকটির কর্ণের দৈর্ঘ্য হবে —–
(a) 10 সেমি.
(b) 6 সেমি.
(c) 2 সেমি.
(d) 12 সেমি.
Ans: (d) 12 সেমি.
সমাধানঃ 2√6 সেমি বাহু বিশিষ্ট দুটি ঘনক পাশাপাশি রাখলে উৎপন্ন আয়তঘনকটির দৈর্ঘ্য (l) = 2√6+2√6 = 4√6 সেমি .
প্রস্থ (b) =2√6 সেমি.
উচ্চতা (h) = 2√6 সেমি.
∴ আয়তঘনকটির কর্ণের দৈর্ঘ্য হবে
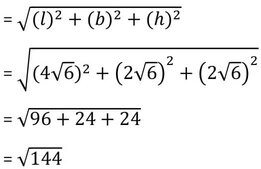
=12 cm.
(vi) x1,x2,x3,…….,x10 রাশিগুলির গড় 20 হলে x1+4 ,x2+4 ,………, x10+4 রাশিগুলির গড় হবে –
(a) 20
(b) 24
(c) 40
(d) 10
Ans: (b) 24
সমাধানঃ x1,x2,x3,…….,x10 রাশিগুলির গড় 20

2. শূন্যস্থান পূরণ করঃ
(i) এক ব্যাক্তি ব্যাঙ্কে 100 টাকা জমা রেখে , 2 বছর পর সমূল চক্রবৃদ্ধি পেলেন 121 টাকা । বার্ষিক সুদে হার ছিল _________ % ।
Ans:
সমাধানঃ ধরি , বার্ষিক সুদের হার r %
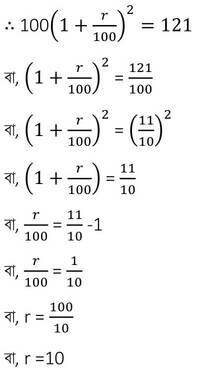
∴ বার্ষিক সুদের হার 10%
(ii) দুটি দ্বিঘাত করণীর যোগফল ও গুনফল একটি মুলদ সংখ্যা হলে করনীদ্বয় ______ করণী ।
Ans: অনুবন্ধী করণী
(iii) দুটি ত্রিভুজের ভূমি একই সরলরেখায় অবস্থিত এবং ত্রিভুজ দুটির অপর শীর্ষবিন্দু সাধারণ হলে , ত্রিভুজ দুটির ক্ষেত্রফলের অনুপাত ভূমির দৈর্ঘ্যের অনুপাতের ___________ ।
Ans: সমান

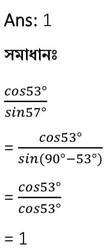
(v) একটি নিরেট লম্ব বৃত্তাকার চোঙের তলসংখ্যা _______ ।
Ansঃ 3 টি
(vi) x1,x2,………,x100 চলগুলি উর্দ্ধক্রমে থাকলে এদের মধ্যমা __________ ।
সমাধানঃ

Madhyamik 2019 Math Question Solution|Madhyamik 2019 Math Question Paper|মাধ্যমিক ২০১৯ গণিত প্রশ্নের সমাধান
3. সত্য বা মিথ্যা লেখ ।
(i) বার্ষিক 10% হারে 100 টাকার 1 বছরের সরল সুদ ও চক্রবৃদ্ধি সুদের পার্থক্য 1 টাকা ।
উত্তরঃ মিথ্যা ।
সমাধানঃ এক্ষেত্রে আসল (P) = 100টাকা
সুদের হার (r ) = 10 %
সময় (t) = 1 বছর
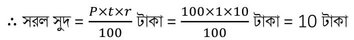

সরল সুদ ও চক্রবৃদ্ধি সুদ সমান ।
(ii) ab:c2 , bc:a2 , ca:b2 –এর যৌগিক অনুপাত 1:1 ।
উত্তরঃ সত্য ।
সমাধানঃ
ab:c2 , bc:a2 , ca:b2 –এর যৌগিক অনুপাত
= (ab)(bc)(ca) = c2a2b2
= a2b2c2 : c2b2c2
= 1:1
(iii) তিনটি অসমরেখ বিব্দু দিয়ে একটি মাত্র বৃত্ত অঙ্কন করা যায় ।
উত্তরঃ সত্য
(iv) sin30° +sin60° > sin90°
উত্তরঃ সত্য।
সমাধানঃ
sin30° +sin60°
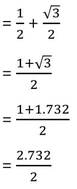
= 1.366 > 1 =sin90°
(v) একই ভূমি ও একই উচ্চতা বিশিষ্ট একটি লম্ব বৃত্তাকার শঙ্কু ও একটি লম্ব বৃত্তাকার চোঙের আয়তনের অনুপাত হবে 1:3
উত্তরঃ 1:3
সমাধানঃ ধরি , লম্ব বৃত্তাকার শঙ্কু ও লম্ব বৃত্তাকার চোঙের ব্যাসার্ধ r একক এবং উচ্চতা h একক ।
∴ এদের আয়তনের অনুপাত
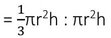
= 1:3
(vi) 2,3,9,10,9,3,9 তথ্যের মধ্যমার মান 10 ।
Ans: মিথ্যা ।
সমাধানঃ সংখ্যা গুলিকে মানের উর্দ্ধক্রমে সাজিয়ে পাই ,
2 ,3,3,9,9,9,10
এক্ষেত্রে n = 7
∴ মধ্যমা = (n+1)/2 তম মান = 8/2 তম মান = 4 তম মান = 9
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাও ।
(i) বার্ষিক 5 % সরল সুদের হারে কত টাকার মাসিক সুদ এক টাকা তা নির্ণয় করি ।
সমাধান
ধরি আসল= x টাকা
শর্তানুসারে ,
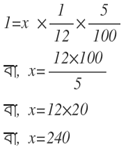
∴ মাসিক সুদ 240 টাকা ।
(ii) একটি অংশীদারী ব্যাবসায় তিনজনের মূলধনের অনুপাত 3:5:8 । প্রথম ব্যাক্তির লাভ তৃতীয় ব্যাক্তির লাভের থেকে 60 টাকা কম হলে ব্যাবসায় মোট কত টাকা লাভ হয়ে ছিল ।
সমাধানঃ ধরি , বাবসায় মোট লাভ হয়েছিল x টাকা ।

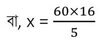
বা, x = 192
∴ ব্যাবসায় মোট লাভ 192 টাকা ।

∴ P =11
(iv) x ∝ y2 এবং y =2a , x =a হলে দেখাও যে y2=4ax ।
সমাধানঃ
x ∝ y2
বা, x =ky2
বা, a = k(2a)2
বা, a = k (4a2)
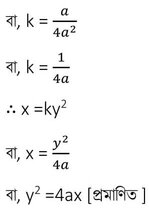

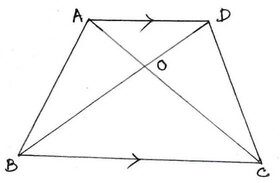
∆AOD ও ∆COB এর ক্ষেত্রে ,
∠OAD = ∠OCD [ একান্তর কোণ,যেহেতু, AD||BC এবং AC ভেদক ]
আবার,∠ODA=∠OCB [একান্তর কোণ,যেহেতু,AD||BC এবং DB ভেদক ]
∠AOD=∠BOC [বিপ্রতীপ কোন]
∴ ∆AOD এবং ∆COB সদৃশকোণী।যেহেতু, সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতী,

(vi) একটি বৃত্তে দুটি জ্যা AB ও AC পরস্পর লম্ব । AB= 4 সেমি. এবং AC =3সেমি. হলে, বৃত্তটির ব্যাসার্ধের দৈর্ঘ্য নির্ণয় কর ।
সমাধানঃ
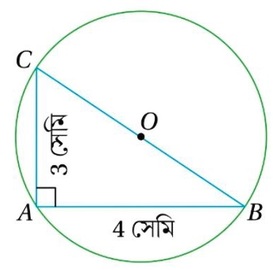
যেহেতু , AB এবং AC জ্যা দুটি পরস্পর লম্ব সুতরাং ACB সমকোণী ত্রিভুজ । AB = 4 সেমি. ও AC = 3 সেমি.
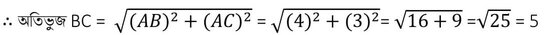
যেহেতু ∠BAC =90
∴ BC হল ব্যাস
∴ ব্যাসার্ধ = BC/2 = 5/2 সেমি. =2.5 সেমি.
(vii) ABC একটি সমকোণী ত্রিভুজের ∠ABC =90° এবং BD⊥AC , যদি AB= 5 সেমি. এবং BC=12 সেমি. হয় তবে BD এর দৈর্ঘ্য নির্ণয় কর ।
সমাধানঃ
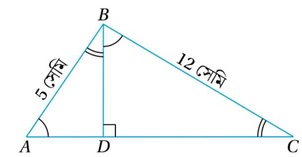
ABC সমকোণী ত্রিভুজে,
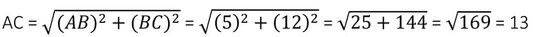
আবার ABC ত্রিভুজের ∠ABC = 90 এবং সমকৌণিক বিন্দু B থেকে অতিভুজ AC এর উপর BD লম্ব । । যেহেতু সমকোণী ত্রিভুজের সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অঙ্কন করলে যে দুটি ত্রিভুজ উৎপন্ন হয় তারা মূল ত্রিভুজের সঙ্গে সদৃশ ।
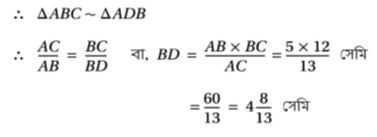
∴ BD = (4 পূর্ণ 8/13) সেমি.
(viii) ϴ(0° ≤ ϴ ≤ 90° ) –এর কোন মান বা মানগুলির জন্য 2sinϴ cosϴ = cosϴ হবে ?
সমাধানঃ 2sinϴ cosϴ = cosϴ
বা, 2sinϴ cosϴ -cosϴ =1
বা, cosϴ (2sinϴ-1) =0
∴ cosϴ = 0
বা, cosϴ = cos90°
বা, ϴ =90°
অথবা ,
(2sinϴ-1)=0
বা, sinϴ = ½
বা, sinϴ = sin30°
বা, ϴ= 30°
∴ ϴ এর মান গুলি হল 90° এবং 30° ।
(ix) sin10ϴ =cos8ϴ এবং 10ϴ ধনাত্মক সূক্ষ্মকোণ হলে , tan 9ϴ এর মান নির্ণয় কর ।
সমাধানঃ
sin10ϴ =cos8ϴ
বা, sin 10ϴ= sin(90°-8ϴ)
বা, 10ϴ = 90° – 8ϴ
বা, 10ϴ+8ϴ = 90°
বা, 18ϴ = 90°
বা, ϴ = 90°/18
বা, ϴ =5°
∴ tan 9ϴ
= tan(9✕5°)
= tan 45°
= 1
(x)একটি আয়তঘনাকৃতি ঘরের দৈর্ঘ্য ,প্রস্থ ও উচ্চতা যথাক্রমে a, b এবং c একক এবং a+b+c= 25, ab+bc+ca = 240.5 হলে ঘরটির মধ্যে যে বৃহত্তম দণ্ডটি রাখা যাবে তাঁর দৈর্ঘ্য নির্ণয় কর ।
সমাধানঃ
a+b+c =25 এবং ab+bc+ca=240.5
এখন , a2+b2+c2 =(a+b+c)2-2(ab+bc+ca)
বা, a2+b2+c2 = (25)2 -2(240.5) =625-481 = 144
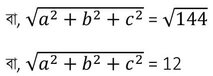
∴ আয়তঘনাকৃতি ঘরের কর্ণের দৈর্ঘ্য 12 একক অর্থাৎ ওই ঘরে সর্বাপেক্ষা যে লম্বা দণ্ডটি রাখা যাবে তার মান 12 একক ।
(xi ) একটি লম্ব বৃত্তাকার শঙ্কুর পার্শ্বতলের ক্ষেত্রফল ভূমির ক্ষেত্রফলের √5 গুন । শঙ্কুটির উচ্চতা ও ভূমির ব্যাসার্ধের অনুপাত নির্ণয় কর ।
সমাধানঃ ধরি, লম্ব বৃত্তাকার শঙ্কুর ব্যাসার্ধ r একক , উচ্চতা h একক এবং তির্যক উচ্চতা l একক ।
∴ লম্ব বৃত্তাকার শঙ্কুর পার্শ্বতলের ক্ষেত্রফল = πrl বর্গ একক এবং ভূমিতলের ক্ষেত্রফল πr2 বর্গ একক
শর্তানুসারে,
πrl = √5✕πr2
বা, l = r√5
বা, l2 = 5r2 [ উভয়পক্ষে বর্গ করে পাই ]
বা, h2+r2 = 5r2 [ l2=h2+r2 ]
বা, h2 = 4r2
বা, h2/r2 = 4:1
বা, h/r = 2/1 [ উভয়পক্ষে বর্গমূল করে পাই ]
বা, h:r = 2:1
∴ শঙ্কুটির উচ্চতা ও ব্যাসার্ধের অনুপাত 2:1 ।
(xii) প্রথম (2n+1) সংখ্যক ক্রমিক স্বাভাবিক সংখ্যার মধ্যবর্তী সংখ্যা (n+103)/3 হলে , n এর মা নির্ণয় কর ।
সমাধানঃ প্রথম (2n+1) সংখ্যক ক্রমিক স্বাভাবিক সংখ্যার মধ্যবর্তী সংখ্যা =(n+1) তম সংখ্যা =(n+1)
∴ (n+1) =(n+103)/3
বা, 3n+3 = n+103
বা, 3n-n = 103-3
বা, 2n = 100
বা, n = 100/2
বা, n = 50
∴ n =50
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
মাধ্যমিকের সকল বিষয়ের বিগত বছরের প্রশ্ন উত্তর (Click Here)
5.

সমাধানঃ আসল (P) = 8000 টাকা
সুদের হার (r) = 10%
6 মাস অন্তর সুদ আসলের সঙ্গে যুক্ত হয় সুতরাং চক্রবৃদ্ধি সুদের পর্ব = 2
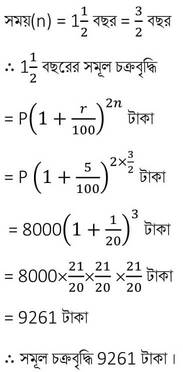
এবং চক্রবৃদ্ধি সুদ = সমূল চক্রবৃদ্ধি – আসল = (9261 – 8000)টাকা = 1261 টাকা ।
(ii) 14. দুই বন্ধু যথাক্রমে 40000 টাকা ও 50000 টাকা দিয়ে একটি যৌথ ব্যাবসা শুরু করেন ।তাদের মধ্যে একটি চুক্তি হয় যে লাভের 50% নিজেদের মধ্যে সমান ভাগে এবং লাভের অবশিষ্ট অংশ মূলধনের অনুপাতে ভাগ হবে । প্রথম বন্ধুর লভ্যাংশের পরিমান যদি দ্বিতীয় বন্ধুর লভ্যাংশ অপেক্ষা 800 টাকা কম হয় , তবে প্রথম বন্ধুর লভ্যাংশ কত ?
সমাধানঃ দুই বন্ধুর মুলধনের অনুপাত = 40000:50000 =4:5
ধরি , মোট লাভ = x টাকা ।
এখন , তাদের মধ্যে চুক্তি অনুযায়ী লাভের 50 % তাদের মধ্যে সমান ভাগে ভাগ হয় এবং বাকি অংশ মূলধনের অনুপাতে ভাগ হয় ।


6.
(i) x2+x+1 =0 সমীকরণের বীজগুলির বর্গ যে সমীকরনের বীজ ,সেই সমীকরণটি নির্ণয় কর ।
সমাধানঃ ধরি, x2+x+1 =0 সমীকরনের বীজগুলি হল a এবং b. আমাদের যে সমীকরণটি নির্ণয় করতে হবে তার বীজগুলি প্রদত্ত সমীকরণের বীজগুলির বর্গ হবে অর্থাৎ a2 এবং b2 বীজ বিশিষ্ট দ্বিঘাতসমীকরণ নির্ণয় করতে হবে ।
x2+x+1 =0 সমীকরনের বীজগুলি হল a এবং b

∴ a+b = -1 এবং ab = 1
এখন , a2+b2
= (a+b)2-2ab
= (-1)2-2(1) [যেহেতু ,a+b = -1 এবং ab = 1]
= 1-2
=-1
এবং a2b2 = (ab)2 =(1)2 =1[∵ab = 1]
নির্ণেয় সমীকরণটি হল ,
x2-(a2+b2)x+a2b2=0
= x2-(-1)x+1=0
= x2+x+1
∴ x2+x+1 এই সমীকরণটি হল সেই সমীকরণ যার বীজগুলি প্রদত্ত দ্বিঘাত সমীকরণের বীজগুলির বর্গ ।
Madhyamik 2019 Math Question Solution|Madhyamik 2019 Math Question Paper Solved|Madhyamik 2019 Math Question Answer|মাধ্যমিক ২০১৯ গণিত প্রশ্নের সমাধান।
(ii) 9. কলমের মূল্য প্রতি ডজনে 6 টাকা কমলে 30 টাকায় আরো তিনটি বেশি কলম পাওয়া যাবে । কমার পূর্বে প্রতি ডজন কলমের মূল্য নির্ণয় করি ।
সমাধানঃ
ধরি প্রতি ডজন কলমের মূল্য x টাকা ।
∴ x টাকায় পাওয়া যাবে 12 টি কলম
1 টাকায় পাওয়া যাবে 12/x টি কলম
30 টাকায় পাওয়া যাবে (30×12)/x টি কলম =360/x টি কলম ।
এখন প্রতি ডজন কলমের মূল্য (x-6) টাকা
∴ (x-6) টাকায় পাওয়া যায় 12 টি কলম
1 টাকায় পাওয়া যায় 12/(x-6) টি কলম
30 টাকায় পাওয়া যায় (30× 12)/(x-6) টি কলম =360/(x-6) টি কলম ।
শর্তানুসারে ,
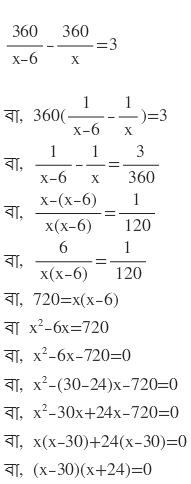
দুটি রাশির গুনফল শূন্য
∴ হয় (x-30)=0
বা, x=30
অথবা, (x+24)=0
বা, x=-24
কলমের মূল্য ঋণাত্মক হতে পারেনা , সুতরাং x=30
অর্থাৎ প্রতি ডজন কলমের মূল্য 30 টাকা ।
7.
(i)

Madhyamik 2019 Math Question Solution

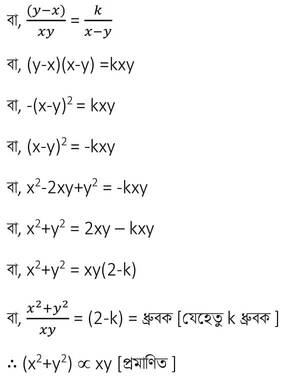
8.
(i) (3x-2y) : (x+3y) = 5:6 হলে, (2x+5y) : (3x+4y) নির্ণয় কর ।
সমাধানঃ
(3x-2y) : (x+3y) = 5:6
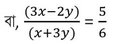
বা, 6(3x-2y) = 5(x+3y)
বা, 18x-12y = 5x+15y
বা, 18x-5x = 12y+15y
বা, 13x = 27y
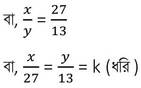
Madhyamik 2019 Math Question Solution
[k (≠0) একটি সমানুপাতিক ধ্রুবক ]
∴ x = 27k এবং y = 13k
∴ (2x+5y) : (3x+4y)
= {2(27k)+5(13k)} : {3(27k) +4(13k)}
= (54k+65k) : ( 81k+52k)
= 119k : 133k
= 119:133
= 17 : 19
∴ (2x+5y) : (3x+4y)= 17 : 19
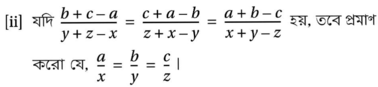

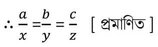
9.
(i) অর্ধ – বৃত্তস্থ কোন সমকোণ – প্রমাণ কর ।
গণিত প্রকাশ বইয়ের (দশম শ্রেণী) উপপাদ্য-37 দেখ ।
(ii) প্রমাণ কর যে , যদি দুটি বৃত্ত পরস্পরকে বহিঃস্পর্শ করে , তাহলে স্পর্শ বিন্দুটি কেন্দ্র দুটির সংযোজক সরল্রেখাংশের ওপর অবস্থিত হবে ।
গণিত প্রকাশ বইয়ের (দশম শ্রেণী) উপপাদ্য-42 দেখ ।
Madhyamik 2019 Math Question Solution
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
মাধ্যমিকের সকল বিষয়ের বিগত বছরের প্রশ্ন উত্তর (Click Here)
10.
(i) O কেন্দ্রীয় বৃত্তের পরিলিখিত চতুর্ভুজ ABCD হলে প্রমাণ কর যে , AB+CD = BC +DA
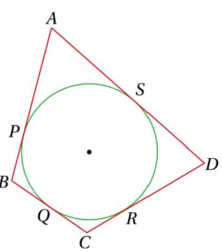
ধরাযাক ABCD চতুর্ভুজটির AB ,BC,CD এবং DA বাহুগুলি বৃত্তটিকে যথাক্রমে P ,Q,R এবং S বিন্দুতে স্পর্শ করেছে । প্রমাণ করতে হবে যে , AB+CD = BC +DA
A বিন্দু থেকে দুটি স্পর্শক AP ও AS টানা হয়েছে ।
∴ AP =AS –(i)
B বিন্দু থেকে দুটি স্পর্শক BP ও BQ অঙ্কন করা হয়েছে
∴ BP = BQ –(ii)
আবার , C বিন্দু থেকে দুটি স্পর্শক CQ ও CR অঙ্কন করা হয়েছে ।
∴ CQ = CR –(iii)
এবং D বিন্দু থেকে দুটি স্পর্শক DS ও DR অঙ্কন অরা হয়েছে
∴ DS =DR —(iv)
এখন AB+CD
= AP+PB +CR+RD
= AS+BQ+CQ+DS [(i) ,(ii) ,(iii) ও (iv) থেকে পাই ]
= (AS+DS) + (BQ+CQ)
= AD+BC [প্রমাণিত ]
Madhyamik 2019 Math Question Solution
(ii) ABC –এর A সমকোণ এবং BP ও CQ দুটি মধ্যমা হলে , প্রমাণ কর যে , 5BC2 = 4(BP2+CQ2)
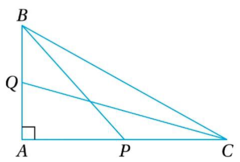
ত্রিভুজ ABC-এর ∠A সমকোণ এবং BP ও CQ দুটি মধ্যমা , প্রমাণ করতে হবে যে 5BC2 = 4(BP2+CQ2)
প্রমাণঃ ABC একটি সমকোণী ত্রিভুজ যার ∠A সমকোণ
∴ BC2
= AB2+AC2
= (2AQ)2 +(2AP)2 [ যেহেতু P ও Q যথাক্রমে AC ও AB এর মধ্যবিন্দু ]
= 4AQ2 +4AP2
আবার সমকোণী ত্রিভুজ BAP ও CAQ থেকে পাওয়া যায় ,
BP2 = AP2+AB2
বা, BP2 = AP2 + (2AQ)2
বা, BP2 = AP2 +4AQ2
এবং CQ2 = AC2 +AQ2
বা, CQ2 = (2AP)2+AQ2
বা, CQ2 = 4AP2 +AQ2
∴ BP2 +CQ2
= AP2 +4AQ2 +4AP2 +AQ2
= 5AP2 +5AQ2
= 5(AP2+AQ2)—(ii)
∴ 5BC2
= 5(4AQ2 +4AP2 ) [(i) থেকে পাই ]
= 4.{5(AQ2+AP2)}
= 4 (BP2 +CQ2) [(ii) থেকে পাই ] [ প্রমাণিত ]
Madhyamik 2019 Math Question Solution|Madhyamik 2019 Math Question Paper Solved|Madhyamik 2019 Math Question Answer|মাধ্যমিক ২০১৯ গণিত প্রশ্নের সমাধান।
11.
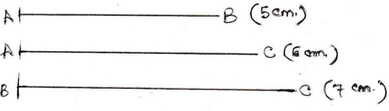
(i) ABC একটি ত্রিভুজ অঙ্কন করো যার BC = 7 সেমি. , AB = 5সেমি. এবং AC =6সেমি. । ABC ত্রিভুজটির পরিবৃত্ত অঙ্কন করো । (কেবলমাত্র অংকন চিহ্ন দিতে হবে )
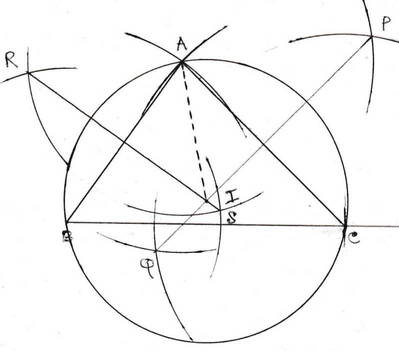
(ii) 4 সেমি ব্যাসার্ধ বিশিষ্ট একটি বৃত্ত অংকন করো । বৃত্তের কেন্দ্র থেকে 6.5 সেমি দূরে কোনো বহিঃস্থ বিন্দু থেকে ওই বৃত্তের দুটি স্পর্শক অংকন করো ।
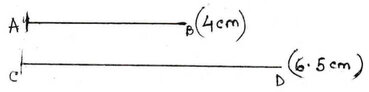
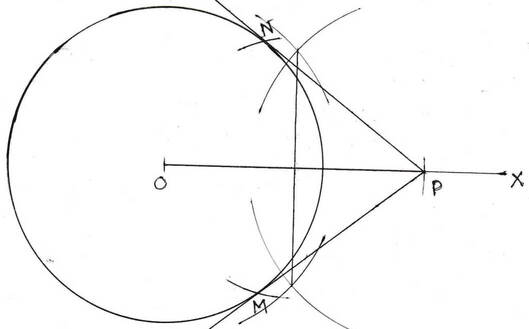
বহিঃস্থ বিন্দু থেকে দুটি স্পর্শক PN এবং PM অংকন করা হল ।
12.
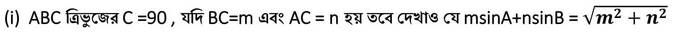
সমাধানঃ
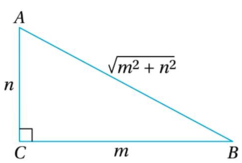
ABC ত্রিভুজের C =90º এবং BC=m একক এবং AC = n একক

(ii)
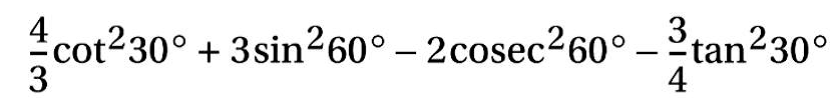
সমাধানঃ
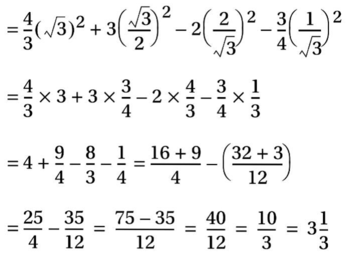

Madhyamik 2019 Math Question Solution
13.
(i) 600 মিটার চওড়া কোনো নদীর একটি ঘাট থেকে দুটি নৌকা ভিন্ন অভিমুখে নদীর ওপারে যাওয়ার জন্য রওনা দিল । যদি প্রথম নৌকাটি নদীর এপারের সঙ্গে 30° কোণ এবং দ্বিতীয় নৌকাটি প্রথম নৌকার গতিপথের সঙ্গে 90° কোণ করে চলে ওপারে পৌঁছায় তাহলে ওপারে পৌঁছানোর পরে নৌকা দুটির দূরত্ব কত হবে ?
সমাধানঃ
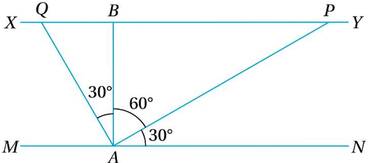
ধরা যাক , MN পাড়ের A বিন্দুস্থ ঘাট থেকে প্রথম নৌকা AP পথে গিয়ে নদীর অপর পাড় XY –এর P বিন্দুতে এবং দ্বিতীয় নৌকা AQ পথে গিয়ে Q বিন্দুতে ওপারে পৌঁছায় ।
AB = নদীর চওড়া = 600 মিটার ।
সুতরাং , ∠PAN = 30°, ∠PAQ = 90°
∴ ∠PAB = 60° এবং ∠BAQ =30°
PQ = নৌকা দুটির দূরত্ব

বা, BP = √3 AB =√3´600
বা, BP = 600√3

∴ PQ = BP+QB = (600√3 + 200√3)মিটার = 800√3 মিটার
∴ নৌকা দুটির দূরত্ব 800√3 মিটার ।
(ii) একটি তিনতলা বাড়ির ছাদে 3.6 মিটার দৈর্ঘ্যের একটি পতাকা আছে । রাস্তার কোনো এক স্থান থেকে দেখলে পতাকা দণ্ডটির চূড়া ও পাদদেশের উন্নতি কোণ যথাক্রমে 50° ও 45° হয় । তিনতলা বাড়ির উচ্চতা হিসাব করে লিখি । [ধরে নাও tan50° = 1.2 ]
সমাধানঃ
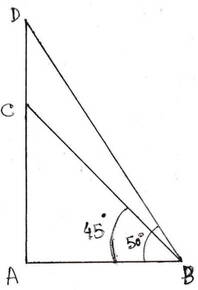
AC হল তিনতলা বাড়ির উচ্চতা এবং CD হল পতাকার দৈর্ঘ্য ।রাস্তার উপর একটি বিন্দু B থেকে পতাকার পাদদেশের অর্থাৎ C বিন্দুর উন্নতি কোণ 45 এবং B বিন্দু থেকে পতাকার চূড়া অর্থাৎ D বিন্দুর উন্নতি কোণ 50।
∴CD =3.6 এবং ∠ABC = 45° এবং ∠ABD = 50°
এখন , ABC ত্রিভুজে ∠BAC =90° এবং ∠ABC =45°
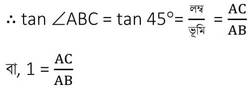
বা, AB =AC —(i)
আবার , ABD ত্রিভুজে ∠BAD = 90° এবং ∠ABD = 50°

বা, 1.2AC = AC+3.6
বা, 1.2AC-AC=3.6
বা, 0.2AC = 3.6
বা, AC =
বা, AC = 18
∴ তিনতলা বাড়ির উচ্চতা 18 মিটার ।
Madhyamik 2019 Math Question Solution
14.
(i) ঘনকাকৃতি একটি সম্পূর্ণ জলপূর্ণ চৌবাচ্চা থেকে সমান মাপের 64 বালতি জল তুলে নিলে চৌবাচ্চাটির 1/3 অংশ জলপূর্ণ থাকে । চৌবাচ্চাটির একটি ধারের দৈর্ঘ্য 1.2 মিটার হলে প্রতিটি বালতিতে কত লিটার জল ধরে হিসাব করে লিখি । ( 1 ঘনডেসিমিটার = 1 লিটার )
সমাধানঃ ঘনকাকৃতি জলপূর্ণ চৌবাচ্চাটির আয়তন
= 1.2✕1.2✕1.2 ঘন মিটার
= 1.728 ঘন মিটার
= 1728 ঘন ডেসিমি
= 1728 লিটার
সমগ্র চৌবাচ্চাটির 1/3 অংশ
= 1/3 ✕ 1.728 ঘনমিটার
= 0.576 ঘন মিটার
= 576 ঘন ডেসিমি
= 576 লিটার
চৌবাচ্চাটি থেকে তুলে নেওয়া জলের পরিমান
= 1728-576
= 1152 লিটার
ধরি প্রতিটি বালতিতে জলধরে = x লিটার
∴64বালতিতে জল ধরে 64x লিটার
শর্তানুসারে ,
64x = 1152
বা, x = 1152 /64
Or, x= 18
∴ প্রতিটি বালতিতে 18 লিটার জল ধরে ।
Madhyamik 2019 Math Question Solution
(ii) একটি তারের প্রস্থচ্ছেদের ব্যাস 50% কমানো হল । আয়তন অপরিবর্তিত রাখতে হলে তারটির দৈর্ঘ্য কত শতাংশ বাড়াতে হবে ?
সমাধানঃ ধরি , তারের প্রস্থচ্ছেদের ব্যাসার্ধ r একক এবং দৈর্ঘ্য h একক ।
∴ ব্যাস = 2r একক
তারের প্রস্থচ্ছেদের ব্যাস 50% কমানো হলে , পরিবর্তিত ব্যাস হবে
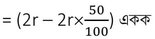
= (2r-r) একক
= r একক
∴ পরিবর্তিত ব্যাসার্ধ = r/2 একক
পূর্বে তারটির আয়তন ছিল = πr2h ঘন একক
ধরা যাক , আয়তন অপরিবর্তিত রাখতে হলে তারটির দৈর্ঘ্য হবে H একক

∴ তারটির দৈর্ঘ্য 300% বৃদ্ধি করতে হবে ।
Madhyamik 2019 Math Question Solution|Madhyamik 2019 Math Question Paper Solved|Madhyamik 2019 Math Question Answer|মাধ্যমিক ২০১৯ গণিত প্রশ্নের সমাধান।
(iii) 6. লম্ব বৃত্তাকার শঙ্কু আকৃতির একটি তাঁবু তৈরি করতে 77 বর্গ মিটার ত্রিপল লেগেছে । তাঁবুটির তির্যক উচ্চতা যদি 7 মিটার হয় ,তবে তাঁবুটির ভূমির ক্ষেত্রফল হিসাব করে লিখি ।
সমাধানঃ লম্ব বৃত্তাকার শঙ্কু আকৃতির একটি তাঁবু তৈরি করতে 77 বর্গ মিটার ত্রিপল লেগেছে ।
অর্থাৎ তাঁবুটির পার্শ্ব তলের ক্ষেত্রফল 77 বর্গ মিটার।
তাঁবুটির তির্যক উচ্চতা (l) = 7 মিটার ।
ধরি, তাঁবুটির ভূমিতলের ব্যাসার্ধ r মিটার ।
শর্তানুসারে ,
πrl = 77

উত্তরঃ তাঁবুটির ভূমিতলের ক্ষেত্রফল 38.5 বর্গ সেমি.।
Madhyamik 2019 Math Question Solution
15.
(i) যদি নীচের পরিসংখ্যা বিভাজন তালিকার যৌগিক গড় 54 হয় , তবে K এর মান নির্ণয় করঃ
| শ্রেণী | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 |
| পরিসংখ্যা | 7 | 11 | K | 9 | 13 |
সমাধানঃ
| শ্রেণী | পরিসংখ্যা (fi) | শ্রেণী মধ্যক (xi) | fixi |
| 0-20 | 7 | 10 | 70 |
| 20-40 | 11 | 30 | 330 |
| 40-60 | K | 50 | 50k |
| 60-80 | 9 | 70 | 630 |
| 80-100 | 13 | 90 | 1170 |
| ∑fi = 40+k | ∑ fixi = 2220+50k |

∴ k =10
Madhyamik 2019 Math Question Solution
মাধ্যমিকের সকল বিষয়ের বিগত বছরের প্রশ্ন উত্তর (Click Here)
(ii) নীচের প্রদত্ত ক্রমযৌগিক পরিসংখ্যা বিভাজন ছকটি থেকে পরিসংখ্যা বিভাজন ছক তৈরি করে তথ্যতির সংখ্যাগুরু মান নির্ণয় করঃ
| শ্রেণী | 10-এর কম | 20-এর কম | 30-এর কম | 40-এর কম | 50-এর কম | 60-এর কম | 70-এর কম | 80-এর কম |
| পরিসংখ্যা | 4 | 16 | 40 | 76 | 96 | 112 | 120 | 125 |
সমাধানঃ প্রদত্ত ক্রমযৌগিক পরিসংখ্যা থেকে পরিসংখ্যা বিভাজন ছক তৈরি করা হলঃ
| শ্রেণি সীমানা | পরিসংখ্যা |
| 0-10 | 4 |
| 10-20 | 16-4=12 |
| 20-30 | 40-16=24 |
| 30-40 | 76-40=36 |
| 40-50 | 96-76=20 |
| 50-60 | 112-96=16 |
| 60-70 | 120-112=8 |
| 70-80 | 125-120=5 |
সংখ্যাগুরু মান সম্বলিত শ্রেণীটি হল (30-40) ।
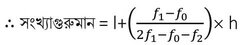
যেখানে , l = সংখ্যাগুরু শ্রেণীর নিম্নসীমানা = 30
f1 = সংখ্যাগুরু শ্রেণীর পরিসংখ্যা = 36
f0 = সংখ্যাগুরু শ্রেণীর ঠিক পূর্ববর্তী শ্রেণীর পরিসংখ্যা = 24
f2 = সংখ্যাগুরু স্রেনির ঠিক পরবর্তী স্রেনির পরিসংখ্যা = 20
h = শ্রেণী দৈর্ঘ্য = 10
∴ সংখ্যাগুরুমান
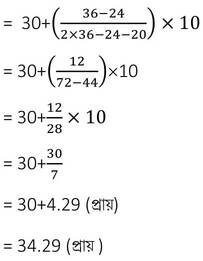
(iii) নীচের তালিকা থেকে একটি বিদ্যালয়ের দশম শ্রেণীর 52 জন ছাত্রের গড় নম্বর প্রত্যক্ষ পদ্ধতি ও কল্পিত গড় পদ্ধতিতে নির্ণয় করঃ
| ছাত্র সংখ্যা | 4 | 7 | 10 | 15 | 8 | 5 | 3 |
| নম্বর | 30 | 33 | 35 | 40 | 43 | 45 | 48 |
সমাধানঃ
| বছর (xi) | ছাত্র সংখ্যা (fi) | fixi | Di = xi-a = xi-40 | fidi |
| 30 | 4 | 120 | -10 | -40 |
| 33 | 7 | 231 | -7 | -49 |
| 35 | 10 | 350 | -5 | -50 |
| 40=a | 15 | 600 | 0 | 0 |
| 43 | 8 | 344 | 3 | 24 |
| 45 | 5 | 225 | 5 | 25 |
| 48 | 3 | 144 | 8 | 24 |
| মোট | ∑fi = 52 | ∑ fixi = 2014 | ∑ fidi =-66 |
প্রত্যক্ষ পদ্ধিতিতে , গড় নম্বর = 2014/52 = 78.73 (প্রায় )
কল্পিত গড় (a) = 40 (ধরা হল )
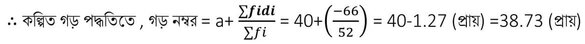
Madhyamik 2019 Math Question Solution|Madhyamik 2019 Math Question Paper Solved|Madhyamik 2019 Math Question Answer|মাধ্যমিক ২০১৯ গণিত প্রশ্নের সমাধান।
Thanks❤
This page helped me a lot of information
Thank you
Thank you very much!!!