সদৃশতা কষে দেখি ১৮.৩|Koshe Dekhi 18.3Class 10|মাধ্যমিক গণিত প্রকাশ দশম শ্রেণি (ক্লাস ১০)(টেন) কষে দেখি 18.3 সমাধান|Ganit Prakash Class 10 Solution Of Chapter 18 Similarity Exercise 18.3|WBBSE Madhyamik Class 10(Ten)(X) Math Solution Of Chapter 18 Similarity|WB Board Math Book Solution In Bengali|Madhyamik Math Solution Of Chapter 18 Koshe Dekhi 18.3
মাধ্যমিক গণিত প্রকাশ বইয়ের সম্পূর্ণ সমাধানের জন্য এখানে CLICK করুন।
সদৃশতা কষে দেখি ১৮.৩|Koshe Dekhi 18.3 Class 10|কষে দেখি 18.3 ক্লাস 10
1. নীচের কোন ত্রিভুজ জোড়া সদৃশ হিসাব করে লিখি।

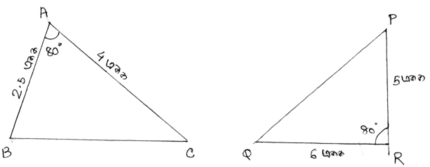
সমাধানঃ প্রথম ত্রিভুজদ্বয়ের ক্ষেত্রে,
স্পষ্টতই, $\frac{AB}{QR}$ = $\frac{BC}{PQ}$ = $\frac{AC}{PR}$ = $\frac{1}{2}$
∴ ∆ABC এবং ∆RQP এর অনুরূপ বাহুগুলি পরস্পর সমানুপাতিক সুতরাং ∆ABC এবং ∆RQP ত্রিভুজদ্বয় পরস্পর সদৃশ ।
দ্বিতীয় ত্রিভুজদ্বয়ের ক্ষেত্রে,
$\frac{AB}{QR} \neq \frac{AC}{PR}$
আবার, $\frac{AB}{PR} \neq \frac{AC}{QR}$
সুতরাং ত্রিভুজদ্বয়ের অনুরূপ বাহুগুলি সমানুপাতি নয় সুতরাং ত্রিভুজদ্বয় সদৃশ নয় ।
সদৃশতা কষে দেখি ১৮.৩|Koshe Dekhi 18.3 Class 10
2. নীচের ত্রিভুজ জোড়া দেখি ও ∠A এর মান হিসাব করে লিখি ।
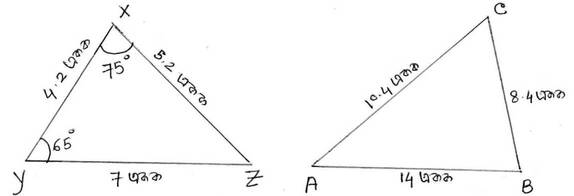
সমাধানঃ
এক্ষেত্রে, $\frac{XY}{BC}$ = $\frac{4.2}{8.4}$ = $\frac{1}{2}$
আবার, $\frac{XZ}{AC}$ = $\frac{5.2}{10.4}$ = $\frac{1}{2}$
এবং $\frac{YZ}{AB}$ = $\frac{7}{14}$ = $\frac{1}{2}$
$\therefore \frac{XY}{BC}$ = $\frac{XZ}{AC}$ = $\frac{YZ}{AB}$
সুতরাং ∆XYZ এবং ∆CAB এর অনুরূপ বাহুগুলি সমানুপাতি ।
∴ ∆XYZ এবং ∆CAB সদৃশকোণী
∴ ∠A =∠Y = 65°
সদৃশতা কষে দেখি ১৮.৩|Koshe Dekhi 18.3 Class 10
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
3. আমাদের মাঠে 6 সেমি. দৈর্ঘ্যের একটি কাঠির 4সেমি. দৈর্ঘ্যের ছায়া মাটিতে পড়েছে । ওই একই সময়ে যদি একটি উঁচু টাওয়ারের ছায়ার দৈর্ঘ্য 28 মিটার হয় , তবে টাওয়ারের উচ্চতা কত হবে হিসাব করে দেখি ।
সমাধানঃ
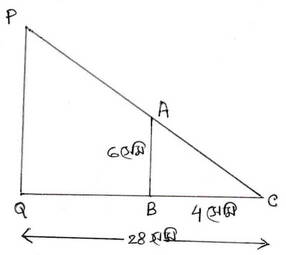
AB এবং PQ খুঁটি দুটি QC ভূমির উপর লম্বভাবে দণ্ডায়মান ।
এক্ষেত্রে AB= 6 মিটার, BC= 4 মিটার, QC =28 মিটার
∴ ∠PQC = ∠ABC = 90°
∴ ∆CPQ এবং ∆CAB এর,
∠CBA = ∠CQP = 90°
এবং ∠C, দুটি ত্রিভুজেরই সাধারণ কোণ
এবং ∠CPQ=∠CAB [অনুরূপ কোণ, যেহেতু, PQ||AB এবং PC ভেদক ]
∴ ∆CPQ এবং ∆CAB সদৃশকোণী
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি পরস্পর সমানুপাতিক
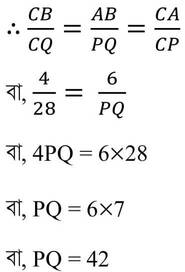
∴ টাওয়ারের উচ্চতা 42 মিটার ।
সদৃশতা কষে দেখি ১৮.৩|Koshe Dekhi 18.3 Class 10
4. প্রমাণ করি যে, কোনো ত্রিভুজের দুটি বাহুর মধ্যবিন্দুর সংযোজক সরলরেখাংশ তৃতীয় বাহুর সমান্তরাল ও অর্ধেক ।
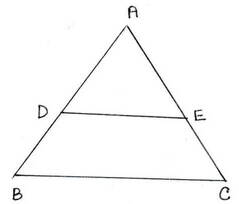
ধরাযাক , ∆ABC এর AB এবং BC বাহুর মধ্যবিন্দু যথাক্রমে D ও E ; প্রমাণ করতে হবে যে, DE || BC এবং DE = ½ BC.
প্রমাণঃ ∆ABC এর AB ও AC বাহুর মধ্যবিন্দুদ্বয় যথাক্রমে D ও E.
∴ AD=DB
এবং AE=EC
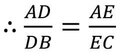
∴ DE || BC [থ্যালেসের বিপরীত উপপাদ্য থেকে পাই ]
এখন , ∆ADE ও ∆ABC এর
∠ADE = ∠ABC [ অনুরূপ কোণ, কারণ DE || BC এবং AB ভেদক]
আবার , ∠AED = ∠ACE [ অনুরূপ কোণ, কারণ DE || BC এবং AC ভেদক]
এবং ∠A দুটি ত্রিভুজেরই সাধারণ কোণ
∴ ∆ADE এবং ∆ABC সদৃশকোণী
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক
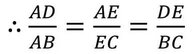
D এবং E যথাক্রমে AB ও AC এর মধ্যবিন্দু ।
∴ AB = 2AD এবং AC = 2AE
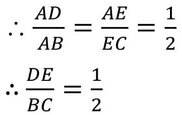
বা, DE = ½ BC [ প্রমাণিত ]
সদৃশতা কষে দেখি ১৮.৩|Koshe Dekhi 18.3 Class 10
5. তিনটি সমবিন্দু সরলরেখাকে দুটি সমান্তরাল সরলরেখা যথাক্রমে A,B,C ও X,Y,Z বিন্দুতে ছেদ করেছে , প্রমাণ করি যে, AB:BC=XY:YZ.
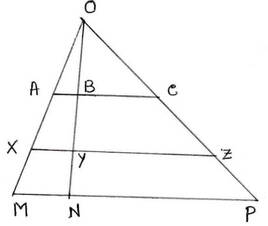
তিনটি সমবিন্দু সরলরেখা হল OM,ON এবং OP, OM,ON এবং OP তিনটি সমবিন্দু সরলরেখাকে দুটি সমান্তরাল সরলরেখা যথাক্রমে A,B,C ও X,Y,Z বিন্দুতে ছেদ করেছে ।প্রমাণ করতে হবে যে, AB:BC= XY:YZ.
প্রমাণঃ এখন ,∆OAB এবং ∆OXY এর,
∴ ∠OAB = ∠OXY [অনুরূপ কোণ, কারণ AC||XZ এবং OX ভেদক]
∠OBA = ∠OYX [ অনুরূপ কোণ, কারণ AC || XZ এবং OY ভেদক ]
∠AOB = ∠XOY [একই কোণ]
∴ ∆OAB এবং ∆OXY সদৃশকোণী
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
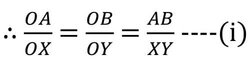
একই ভাবে প্রমাণ করা যায়, ∆OBC এবং ∆OYZ সদৃশকোণী,
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
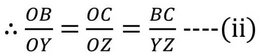
(i) ও (ii) থেকে পাই,
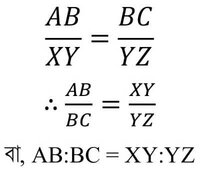
∴ AB:BC = XY:YZ [ প্রমাণিত ]
সদৃশতা কষে দেখি ১৮.৩|Koshe Dekhi 18.3 Class 10
মাধ্যমিক গণিত প্রকাশ বইয়ের সম্পূর্ণ সমাধানের জন্য এখানে CLICK করুন।
6. PQRS একটি ট্রাপিজিয়াম অঙ্কন করেছি যার PQ || SR; PR ও QS কর্ণদুটি O বিন্দুতে পরস্পরকে ছেদ করলে , প্রমাণ করি যে, OP:OR=OQ:OS ; যদি SR=2PQ হয়, তাহলে প্রমাণ করি যে, O বিন্দু কর্ণ দুটির প্রত্যেকটির সমত্রিখন্ডক বিন্দুর একটি বিন্দু হবে ।
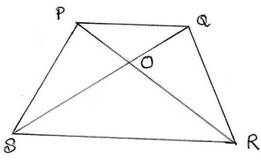
PQRS একটি ট্রাপিজিয়াম, যার PQ || SR; PR ও QS কর্ণদুটি O বিন্দুতে পরস্পরকে ছেদ করেছে । প্রমাণ করতে হবে যে, OP:OR=OQ:OS ; যদি SR=2PQ হয়, তাহলে প্রমাণ করতে হবে যে, O বিন্দু কর্ণ দুটির প্রত্যেকটির সমত্রিখন্ডক বিন্দুর একটি বিন্দু হবে । অর্থাৎ প্রমাণ করতে হবে যে, OP:OR=OQ:OS=1:2
প্রমাণঃ ∆OPQ এবং ∆ORS এর,
∠OPQ = ∠ORS [ একান্তর কোণ, কারণ PQ||SR এবং PR ভেদক]
∠OQP = ∠OSR [ একান্তর কোণ, কারণ PQ||SR এবং QS ভেদক ]
এবং ∠POQ = ∠ROS [ বিপ্রতীপ কোণ ]
∴ ∆OPQ এবং ∆ORS সদৃশকোণী
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
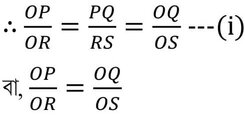
∴ OP:OR=OQ:OS [ প্রমাণিত ]
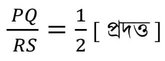
∴ (i) নং সমীকরণ থেকে পাই,
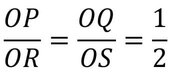
∴ OP:OR=OQ:OS=1:2 [ প্রমাণিত ]
সদৃশতা কষে দেখি ১৮.৩|Koshe Dekhi 18.3 Class 10
7.PQRS একটি সামান্তরিক । S বিন্দুগামী একটি সরলরেখা PQ ও বর্ধিত RQ –কে যথাক্রমে X ও Y বিন্দুতে ছেদ করলে , প্রমাণ কর যে PS:PX= QY:QX=RY:RS.
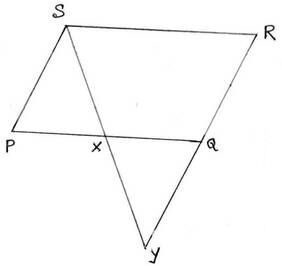
PQRS একটি সামান্তরিক, S বিন্দুগামী একটি সরলরেখা PQ ও বর্ধিত PQ কে X ও Y বিন্দুতে ছেদ করেছে, প্রমাণ করতে হবে যে, PS:PX= QY:YZ=RY:RS.
প্রমাণঃ ∆XSP এবং ∆XYQ এর ,
∠XSP = ∠XYQ [ একান্তর কোণ,কারণ SP||QYএবং SYভেদক]
∠SXP = ∠YXQ [ বিপ্রতীপ কোণ ]
এবং ∠SPX = ∠YQX [ একান্তর কোণ,কারণ SP||QYএবং PQ ভেদক]
∴ ∆XSP এবং ∆XYQ সদৃশকোণী
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
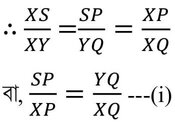
আবার , ∆YQX এবং ∆YRS এর ,
∠YXQ = ∠YSR [অনুরূপ কোণ, কারণ PQ||SR এবং YS ভেদক]
∠YQX = ∠YRS [ অনুরূপ কোণ, কারণ PQ||SR এবং YR ভেদক ]
∠Y দুটি ত্রিভুজেরই সাধারণ কোণ
∴ ∆YQX এবং ∆YRS সদৃশকোণী।
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
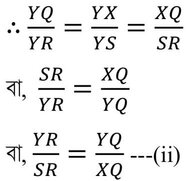
(i) ও (ii) থেকে পাই,
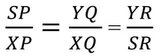
∴ SP:XP=YQ:XQ=YR:SR
বা, PS:PX = QY:QX = RY:RS [ প্রমাণিত ]
সদৃশতা কষে দেখি ১৮.৩|Koshe Dekhi 18.3 Class 10
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
8. দুটি সূক্ষ্মকোণী ত্রিভুজ ∆ABC ও ∆PQR সদৃশকোণী । তাদের পরিকেন্দ্র যথাক্রমে X এবং Y ;BC ও QR অনুরূপ বাহু হলে, প্রমাণ করি যে, BX:QY=BC:QR.
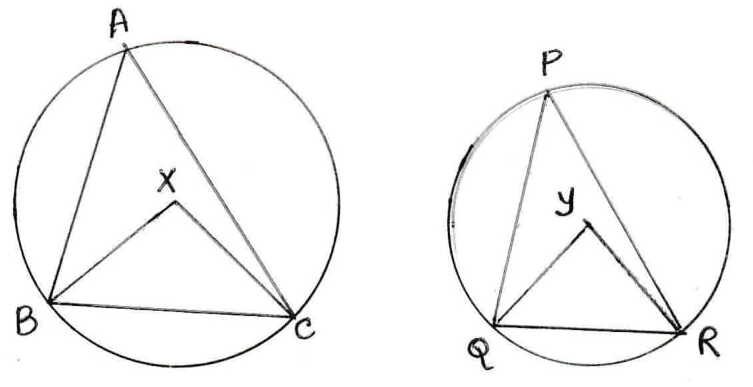
সমাধানঃ দুটি সূক্ষ্মকোণী ত্রিভুজ ∆ABC ও ∆PQR সদৃশকোণী।
∴ ∠A=∠P, ∠B=∠Q এবং ∠C=∠R.
X ও Y যথাক্রমে ∆ABC এবং ∆PQR এর পরিকেন্দ্র ।
BC বৃত্তচাপের উপর ∠BXC কেন্দ্রস্থ কোন এবং ∠BAC পরিধিস্থ কোণ ।
∴ ∠BXC=2∠BAC
আবার, QR বৃত্তচাপের উপর ∠QYR কেন্দ্রস্থ কোন এবং ∠QPR পরিধিস্থ কোণ
∴ ∠QYR=2∠QPR
আবার , ∠BAC=∠QPR, ∴ ∠BXC=∠QYR
এখন ,BX =XC [ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠XBC = ∠XCB
ধরি, ∠XBC = ∠XCB =a
ত্রিভুজ ∆BXC থেকে পাই,
∠XBC + ∠XCB+∠BXC = 180
বা, a+a = 180º-∠BXC
বা, 2a = 180º-∠BXC
বা, a = (180º-∠BXC)/2
আবার, YQ = YR[ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠YQR=∠YRQ
ধরি , ∠YQR = ∠YRQ = b
এখন ∆QYR থেকে পাই,
∠YQR+∠YRQ+∠QYR=180º
বা, b+b= 180º-∠QYR
বা, 2b= 180º-∠QYR
বা, b = (180º-∠QYR)/2
এখন , (180º-∠BXC)/2 = (180º-∠QYR)/2 [ যেহেতু,∠BXC = ∠QYR ]
∴ a=b
∴ ∆BXC এবং ∆QYR এর ∠XBC = ∠YQR , ∠XCB = ∠YRQ এবং ∠BXC = ∠QYR.
সুতরাং ∆BXC এবং ∆QYR সদৃশকোণী
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
∴ BX:QY = BC:QR = XC:YR
∴ BX:QY = BC:QR [ প্রমাণিত ]
সদৃশতা কষে দেখি ১৮.৩|Koshe Dekhi 18.3 Class 10
9. কোনো বৃত্তের PQ ও RS দুটি জ্যা বৃত্তের অভ্যন্তরে X বিন্দুতে পরস্পরকে ছেদ করেছে ।P,S ও R,Q যুক্ত করে , প্রমাণ করি যে, ∆PXS ও ∆RSQ সদৃশকোণী । এর থেকে প্রমাণ করি যে, PX.XQ = RX.XS.অথবা একটি বৃত্তে দুটি জ্যা পরস্পরকে অন্তঃস্থ ভাবে ছেদ করলে একটির অংশদ্বয়ের আয়তক্ষেত্র অপরটির অংশদ্বয়ের আয়তক্ষেত্রের সমান হবে।
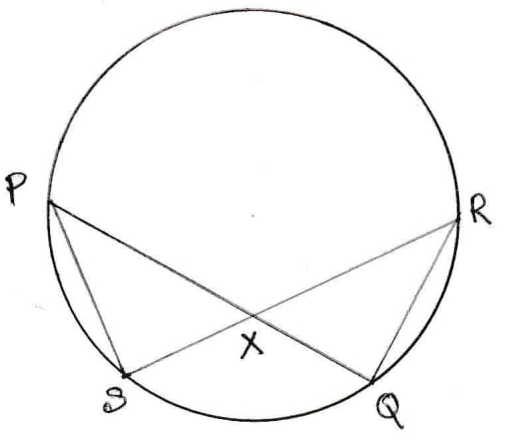
PQ ও RS দুটি জ্যা বৃত্তের অভ্যন্তরে X বিন্দুতে পরস্পরকে ছেদ করেছে , PS ও RQ যুক্ত করা হল , প্রমাণ করতে হবে যে ∆PXS এবং ∆RSQ সদৃশকোণী । আরও প্রমাণ করতে হবে যে, PX.XQ = RX.XS
প্রমাণঃ ∆PXS এবং ∆RXQ ত্রিভুজের ক্ষেত্রে ,
∠XPS=∠XRQ [ যেহেতু একই বৃত্তাংশস্থ সকল কোণের মান সমান ]
∠XSP=∠XQX [ যেহেতু একই বৃত্তাংশস্থ সকল কোণের মান সমান ]
∠PXS =∠RXQ [ বিপ্রতীপ কোণ ]
∴ ∆PXS এবং ∆RXQ সদৃশকোণী [প্রমাণিত ]
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
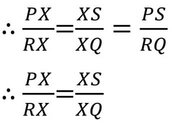
বা, PX.XQ = RX.XS [ প্রমাণিত ]
সদৃশতা কষে দেখি ১৮.৩|Koshe Dekhi 18.3 Class 10
10. একটি সরলরেখার উপর P ও Q দুটি বিন্দু । P এবং Q বিন্দুতে সরলরেখাটির উপর যথাক্রমে PR এবং QS লম্ব । PS এবং QR পরস্পরকে O বিন্দুতে ছেদ করে । OT, PQ – এর উপর লম্ব । প্রমাণ করি যে , 1/OT=1/PR+1/QS
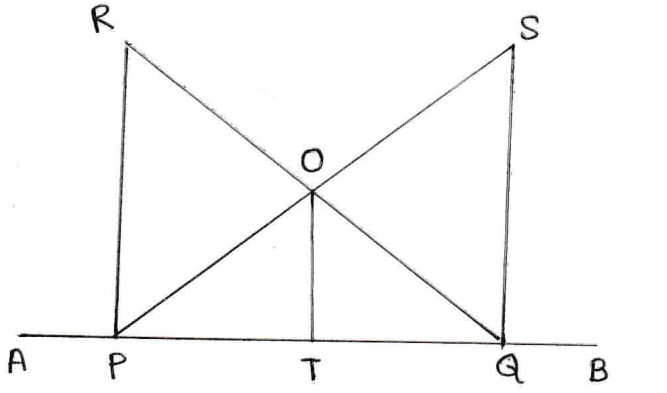
AB সরলরেখার উপর P ও Q যেকোনো দুটি বিন্দু । P ও Q বিন্দুতে PR ও QS লম্ব অঙ্কন করা হল । PR ও QS পরস্পরকে O বিন্দুতে ছেদ করে, OT , PQ-এর উপর লম্ব । প্রমাণ করতে হবে যে ,
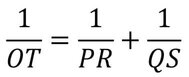
প্রমাণঃ ∆RPQ এবং ∆OTQ এর মধ্যে ,
∠RPQ =∠OTQ [উভয়ই 1 সমকোণ ]
∠RQP = ∠OQT [ একই কোণ ]
∠PRQ = ∠TOQ [অনুরূপ কোণ,যেহেতু , PR || TO এবং RQ ভেদক]
∴ ∆OTQ এবং ∆RPQ সদৃশকোণী
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
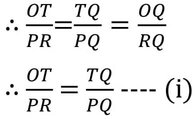
আবার ,∆SPQ এবং ∆OPT এর মধ্যে
∠SQP = ∠OTP [উভয়ই 1 সমকোণ ]
∠SPQ = ∠OPT [একই কোণ ]
∠PSQ =∠POT [অনুরূপ কোণ,যেহেতু , OT || SQ এবং PS ভেদক ]
∴ ∆OPT এবং ∆SPQ সদৃশকোণী
এবং সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
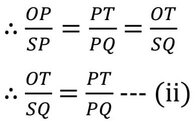
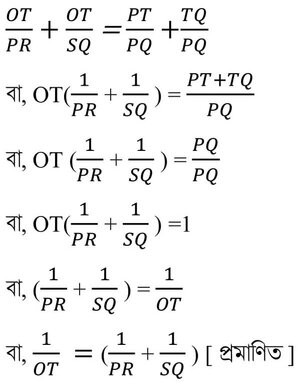
(i) ও (ii) যোগ করে পাই ,
সদৃশতা কষে দেখি ১৮.৩|Koshe Dekhi 18.3 Class 10
মাধ্যমিক গণিত প্রকাশ বইয়ের সম্পূর্ণ সমাধানের জন্য এখানে CLICK করুন।
11. একটি বৃত্তে অন্তর্লিখিত ∆ABC ; বৃত্তের ব্যাস AD এবং AE, BC বাহুর উপর লম্ব যা BC বাহুকে E বিন্দুতে ছেদ করে । প্রমাণ করি যে, ∆AEB এবং ∆ACD সদৃশকোণী । এর থেকে প্রমাণ করি যে , AB.AC = AE.AD.
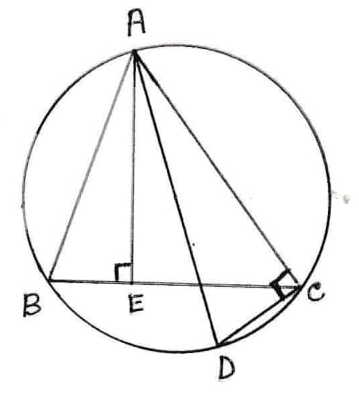
ABC ত্রিভুজটি বৃত্তে অন্তর্লিখিত, যার ব্যাস AD ,AE , BC বাহুর উপর লম্ব যা BC বাহুকে E বিন্দুতে ছেদ করেছে । প্রমাণ করতে হবে যে ,∆AEB এবং ∆ACD সদৃশকোণী,আরও প্রমাণ করতে হবে যে, AB.AC = AE.AD.
প্রমাণঃ ∆AEB এবং ∆ACD ত্রিভুজের ক্ষেত্রে ,
∠AEB = ∠ACD = 90º
∠ABE =∠ADC [ যেহেতু,একই বৃত্তাংশস্থ সকল কোণের মান সমান ]
∠BAE = ∠DAC [ অবশিষ্ট কোণ ]
∴ ∆AEB এবং ∆ACD সদৃশকোণী
যেহেতু সদৃশকোণী ত্রিভুজের অনুরূপ বাহুগুলি সমানুপাতিক।
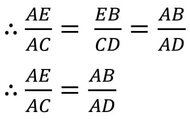
∴ AB.AC = AE.AD [ প্রমাণিত ]
সদৃশতা কষে দেখি ১৮.৩|Koshe Dekhi 18.3 Class 10
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে