Koshe Dekhi 24 Class 10|পূরক কোণের ত্রিকোণমিতিক অনুপাত কষে দেখি ২৪

Koshe Dekhi 24 Class 10|পূরক কোণের ত্রিকোণমিতিক অনুপাত কষে দেখি ২৪|Koshe Dekhi 24 Class10|Trigonometric Ratios Of Complementary Angle|WBBSE Madhyamik Ganit Prakash Class 10(Ten) (X) Math Solution Of Chapter 24|WB Board Class 10 Math Book Solution.

মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন

মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন

WBBSE Official Site.

Koshe Dekhi 24 Class 10|পূরক কোণের ত্রিকোণমিতিক অনুপাত কষে দেখি ২৪|কষে দেখি 24 ক্লাস 10

Koshe Dekhi 24 Class 10|পূরক কোণের ত্রিকোণমিতিক অনুপাত কষে দেখি ২৪

2. দেখাই যে :

(i) sin66°-cos24°= 0

sin66°-cos24°

= sin66° – cos(90°-66°)

= sin66°-sin66° [যেহেতু cos(90°-ϴ)=sinϴ]

= 0 [প্রমাণিত ]

(ii) cos²57° + cos² 33°=1

cos²57° + cos² 33°

= cos²57° + cos² (90°-57°)

= cos² 57° + sin² 57° [যেহেতু, cos(90°-ϴ)=sinϴ]

= 1 [যেহেতু , sin²ϴ+cos² ϴ=1]

∴ cos²57° + cos² 33°=1 [প্রমাণিত]

(iii) cos² 75° -sin²15°=0

cos² 75° -sin²15°

= cos² 75° – sin² (90°-75°)

= cos² 75° – cos² 75°[যেহেতু ,sin(90°-ϴ)=cosϴ]

= 0 [প্রমাণিত ]

(iv) cosec ²48°-tan²42°=1

cosec ²48°-tan²42°

=cosec² 48° – tan²(90°-48°)

= cosec² 48° – Cot² 48^° [যেহেতু tan(90°-ϴ) = cotϴ]

= 1 [প্রমাণিত ] [যেহেতু cosec² ϴ-cot²ϴ=1]

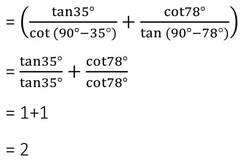
(v) sec70°sin20°+cos20°cosec70°=2

sec70°sin20°+cos20°cosec70°

=sec(90°-20°)sin20°+cos(90°-70°)cosec70°

= cosec20° sin20° + sin70° cosec70° [যেহেতু sec(90°-ϴ)=cosecϴ এবং  cos(90°-ϴ)=sinϴ]

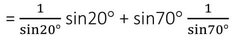
= 1+1

= 2 [ প্রমাণিত ]

3. যদি α ও β কোণ দুটি পরস্পর পূরক কোণ হয় , তাহলে দেখাই যে ,

(i) sin² α+sin² β =1

সমাধানঃ

যেহেতু α ও β কোণ দুটি পরস্পর পূরক কোণ

∴ α+β =90°

বা, β = 90°-α

∴ sin² α+sin²β

= sin²α + sin² (90°-α)

= sin²α+cos²α  [যেহেতু sin(90°-ϴ)=cosϴ]

= 1

∴ sin² α+sin² β=1 [প্রমাণিত ]

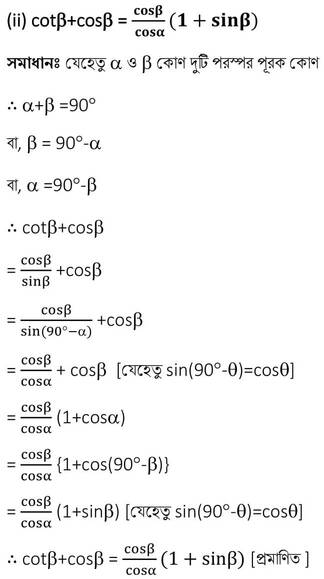
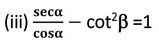
সমাধানঃ

যেহেতু αও β কোণ দুটি পরস্পর পূরক কোণ

∴ α+β =90°

বা, β = 90°-α

সমাধানঃ

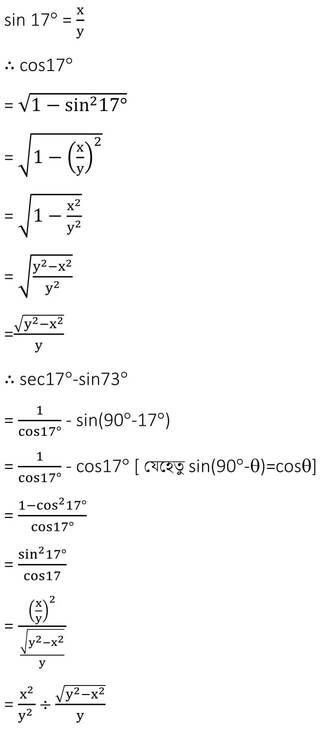
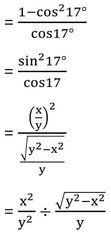
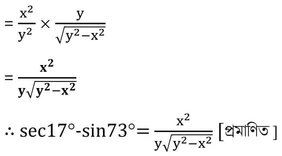
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন

সমাধানঃ

7. দেখাই যে , cosec²22° cot²68° = sin²22° +sin²68° +cot² 68°

সমাধানঃ

বামপক্ষঃ

cosec²22° cot²68°

= cosec²22° cot² (90°-22°)

= cosec² 22° tan² 22°

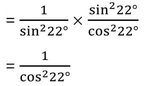
= sec²22°

= sec²(90°-68°)

= cosec² 68°

ডানপক্ষঃ

sin²22° +sin²68° +cot² 68°

= sin²22°+sin²(90°-22°)+cot²68°

= sin²22°+cos²22°+cot²68°

= 1+cot² 68°

= cosec²68°

∴ বামপক্ষ = ডানপক্ষ [ প্রমাণিত ]

সমাধানঃ

P+Q=90°

বা, Q = 90°-P

বামপক্ষঃ

= cosP = ডানপক্ষ

∴ বামপক্ষ = ডানপক্ষ [ প্রমাণিত ]

Koshe Dekhi 24 Class 10|পূরক কোণের ত্রিকোণমিতিক অনুপাত কষে দেখি ২৪

সমাধানঃ

cot12° cot38° cot52° cot78°cot60°

=cot12° cot38° cot(90°-38°) cot(90°-12°) cot60°

= cot12° cot38° tan38° tan12° cot60°

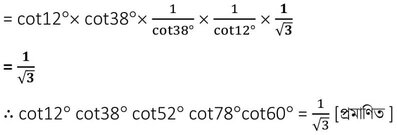
10. O কেন্দ্রীয় যেকোনো একটি বৃত্তের AOB একটি ব্যাস এবং বৃত্তের উপর C যেকোনো একটি বিন্দু । এবার A,C ;B,C এবং O ,C যুক্ত করে দেখাই যে,

(i) tan ∠ABC = cot ∠ACO

(ii) sin² ∠BCO +sin² ∠ACO =1

(iii) cosec² ∠CAB-1=tan² ∠ABC

সমাধানঃ

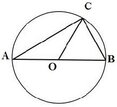
O কেন্দ্রীয় বৃত্তের AOB একটি ব্যাস । A,C ;B,C এবং O,C যুক্ত করা হল ।

স্পষ্টতই ∠ACB =90° [ যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ ]

∴ ∠ACO+∠BCO =90°

বা, ∠ACO =90°-∠BCO

এবং ABC ত্রিভুজে ∠CAB +∠ABC=90°

বা, ∠ABC = 90°-∠CAB

বা, ∠CAB = 90°-∠ABC

(i) tan ∠ABC

= tan (90°-∠CAB) [যেহেতু ∠ABC = 90°-∠CAB]

=cot ∠CAB [যেহেতু tan(90°-ϴ)=cotϴ]

= cot ∠ACO [ যেহেতু ∠CAB =∠ACO কারণ OC=OA(একই বৃত্তের ব্যাসার্ধ)]

∴ tan ∠ABC = cot ∠ACO [প্রমাণিত ]

(ii) sin² ∠BCO+sin² ∠ACO

= sin² ∠BCO + sin² (90°-∠BCO) [যেহেতু ∠ACO =90°-∠BCO]

= sin² ∠BCO +cos² ∠BCO [যেহেতু sin(90°-ϴ)=cosϴ]

= 1

∴ sin² ∠BCO+sin²∠ACO =1[প্রমাণিত ]

(iii) cosec² ∠CAB -1

= cosec²(90°-∠ABC)-1 [যেহেতু ∠CAB = 90°-∠ABC]

= sec²∠ABC -1 [যেহেতু cosec(90°-ϴ)=secϴ]

= tan² ∠ABC

∴ cosec² ∠CAB -1 = tan² ∠ABC [প্রমাণিত ]

Koshe Dekhi 24 Class 10|পূরক কোণের ত্রিকোণমিতিক অনুপাত কষে দেখি ২৪

11.ABCD একটি আয়তকার চিত্র । A,C যুক্ত করে প্রমাণ করি যে ,

(i) tan∠ACD = cot∠ACB

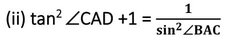
সমাধানঃ

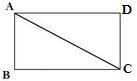
যেহেতু ABCD একটি আয়তক্ষেত্র

∴ ∠BCD =90°

বা, ∠ACB+∠ACD =90°

বা, ∠ACD = 90°-∠ACB

এবং ∠BAD=90°

বা, ∠BAC+∠CAD=90°

বা, ∠CAD = 90°-∠BAC

(i) tan ∠ACD

= tan (90°-∠ACB) [যেহেতু, ∠ACD=(90°-∠ACB)]

= cot ∠ACB [যেহেতু, tan (90°-ϴ)=cotϴ]

∴ tan ∠ACD= cot ∠ACB [প্রমাণিত ]

(ii) tan² ∠CAD +1

= tan ² (90°-∠BAC)+1 [ যেহেতু∠CAD=(90°-∠BAC)]

= cot² ∠BAC +1 [যেহেতু tan (90°-ϴ)=cotϴ]

= cosec ² ∠BAC

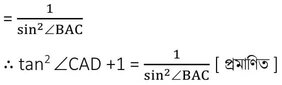
12. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)

(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.)

(i) (sin43°cos47° +cos43°sin47° )-এর মান

(a) 0

(b) 1

(c ) sin4°

(d) cos4°

Ans: (b) 1

সমাধানঃ 

(sin43°cos47° +cos43°sin47° )

= sin43° cos(90°-43°) + cos43° sin(90°-43°)

= sin43°✕ sin43° +cos43°✕ cos43°

= sin²43° +cos²43°

= 1

Koshe Dekhi 24|পূরক কোণের ত্রিকোণমিতিক অনুপাত|কষে দেখি ২৪

(iii) {cos(40°+ϴ)-sin(50°-ϴ)}-এর মান

(a) 2cosϴ

(b) 7sinϴ

(c ) 0

(d) 1

Ans: (c ) 0

সমাধানঃ

{cos(40°+ϴ)-sin(50°-ϴ)}

= cos(40°+ϴ)-sin{90°-(40°+ϴ)}

= cos(40°+ϴ) – cos(40°+ϴ)

= 0

(a) sin A/2

(b) cosA/2

(c ) sinA

(d) cosA

Ans: (b) cosA/2

সমাধানঃ

= cos A/2

(v) A+B=90° এবং tan A =3/4 হলে CotB –এর মান

(a) ¾

(b) 4/3

(c ) 3/5

(d) 4/5

Ans: (a) ¾

সমাধানঃ A+B =90°

বা, B = 90°-A

∴ cotB

= cot(90°-A)

= tanA

= ¾

(B) নীচের বিবৃতি গুলি সত্য না মিথ্যা লিখিঃ

(i) cos54° এবং sin36° এর সরলতম মান সমান ।

উত্তরঃ সত্য

সমাধানঃ cos 54° = cos(90°-36°) =sin36°

(ii) (sin12°-cos78°)-এর সরলতম মান 1.

উত্তরঃ মিথ্যা

সমাধানঃ (sin12°-cos78°)

= sin12° – cos(90°-12°)

= sin12°-sin12°

= 0

মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন

(C ) শূন্যস্থান পূরণ করিঃ

(i) (tan15°✕tan45°✕tan60°✕tan75°)-এর মান _____

উত্তরঃ √3

সমাধানঃ (tan15°✕tan45°✕tan60°✕tan75°)

= tan 15°✕1✕√3✕tan(90°-15°)

= tan15° ✕√3 ✕ cot15°

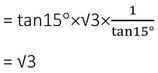
(ii) (sin12°✕cos18°✕sec78°✕cosec72°)-এর মান ______

উত্তরঃ 1

সমাধানঃ (sin12°✕ cos18° ✕ sec78° ✕ cosec72°)

= sin12°✕ cos18° ✕ sec(90°-12°)✕ cosec(90°-18°)

= sin12°✕cos18°✕cosec12°✕ sec18°

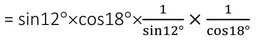
= 1

(iii) A এবং B পরস্পর পূরক কোণ হলে, sinA = _____

উত্তরঃ cosB

সমাধানঃ যেহেতু A এবং B পরস্পর পূরক

∴ A+B =90°

বা, A = 90°-B

sinA = sin(90°-B) =cosB

Koshe Dekhi 24 Class 10|পূরক কোণের ত্রিকোণমিতিক অনুপাত কষে দেখি ২৪

13. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)

(i) sin10ϴ = cos8ϴ এবং 10ϴ ধনাত্মক সূক্ষ্মকোণ হলে , tan9ϴ এর মান নির্ণয় করি ।

সমাধানঃ sin10ϴ = cos8ϴ

বা, sin 10ϴ = sin(90°-8ϴ)

বা, 10ϴ=90°-8ϴ

বা, 18ϴ =90°

বা, ϴ= 90°/18

বা, ϴ=5°

∴ tan9ϴ

= tan (9✕5°)

= tan45°

=1

∴ tan9ϴ=1

(ii) tan4ϴ✕ tan6ϴ=1 এবং 6ϴ ধনাত্মক সূক্ষ্মকোণ হলে , ϴএর মান নির্ণয় করি ।

সমাধানঃ tan4ϴ✕tan6ϴ=1

বা, tan6ϴ= 1/tan4ϴ

বা, tan6ϴ = cot4ϴ

বা, tan6ϴ = tan(90°-4ϴ)

বা, 6ϴ=90°-4ϴ

বা, 10ϴ = 90°

বা, ϴ = 90°/10

বা, ϴ = 9°

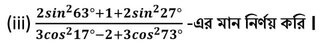
সমাধানঃ

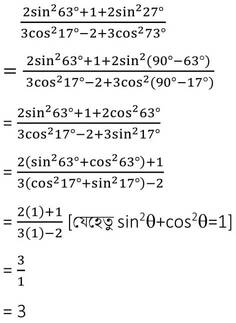
(iv) (tan1°✕tan2°✕tan3°……………. tan89°)

সমাধানঃ

(tan1°✕tan2°✕tan3°……. tan89°)

=tan1°✕tan2°✕tan3°……tan44°✕tan45°✕tan46°…….tan87°✕tan88°✕tan89°

=tan1°✕tan2°✕tan3°…….tan44°✕1✕tan(90°-44°)…….tan(90°-3°)✕tan(90°-2°)✕tan(90°-1°)

=tan1°✕tan2°✕tan3°……tan44°✕cot44°……cot3°✕cot2°✕cot1°

=(tan1°✕cot1°)✕(tan2°✕cot2°)✕(tan3°✕cot3°)……(tan44°✕cot44°)

=1✕1✕1…..1 [যেহেতু tanϴ✕cotϴ=1]

=1

(v) sec5A=cosec(A+36°) এবং 5A ধনাত্মক সূক্ষ্মকোণ হলে ,A এর মান নির্ণয় করি ।

সমাধানঃ  sec5A=cosec(A+36°)     

বা, sec5A = sec{90°-(A+36°)} [যেহেতু sec(90°-ϴ)=cosecϴ]

বা, 5A = 90°-(A+36°)

বা, 5A=90°-A-36°

বা, 5A+A=90°-36°

বা, 6A = 54°

বা, A =54°/6

বা, A =9°     

মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন

এই পোস্টটি আপনাদের ভাল লাগলে SHARE করার অনুরোধ রইল । এইরকম আরও পোস্ট পেতে, আমাদের FACEBOOK PAGE টি LIKE করুন ।