Koshe Dekhi 25 Class 10|উচ্চতা ও দূরত্ব কষে দেখি ২৫ ক্লাস ১০|Koshe Dekhi 25 Class10|WBBSE Madhyamik Ganit Prakash Class 10(Ten) (X) Math Solution Of Chapter 25|WB Board Class 10 Math Solution Of Chapter 25.
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
Koshe Dekhi 25 Class 10|উচ্চতা ও দূরত্ব কষে দেখি ২৫ ক্লাস ১০|কষে দেখি 25 ক্লাস 10
1. একটি নারকেল গাছের গোড়া থেকে অনুভূমিক তলে 20 মিটার দূরের একটি বিন্দুর সাপেক্ষে গাছটির অগ্রভাগের উন্নতি কোণ যদি 60° হয় ,তাহলে গাছটির উচ্চতা নির্ণয় কর ।
সমাধানঃ
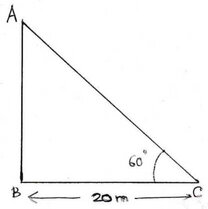
ধরি , AB নারকেল গাছের গোড়া B থেকে 20 মিটার দূরে C বিন্দু থেকে গাছটির অগ্রভাগ অর্থাৎ A বিন্দুর উন্নতি কোণ ∠ACB = 60°
এখন সমকোণী ত্রিভুজ ABC এর ক্ষেত্রে ,

বা, AB = 20√3
∴ নারকেল গাছের উচ্চতা 20√3 মিটার ।
Koshe Dekhi 25 Class 10|উচ্চতা ও দূরত্ব কষে দেখি ২৫ ক্লাস ১০
2. সূর্যের উন্নতি কোণ যখন 30° তখন স্তম্ভের ছায়ার দৈর্ঘ্য 9 মিটার হয় । স্তম্ভটির উচ্চতা হিসাব করে লিখি ।
সমাধানঃ
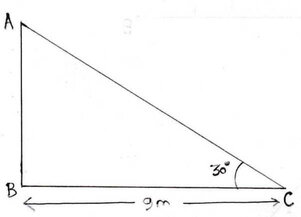
ধরাযাক , AB হল স্তম্ভটির দৈর্ঘ্য । সূর্যের উন্নতি কোণ যখন 30° তখন স্তম্ভের ছায়ার দৈর্ঘ্য BC=9মিটার ।
এখন ABC ত্রিভুজের ∠ABC = 90° এবং ∠ACB = 30°
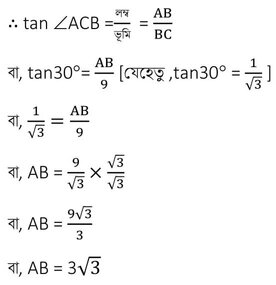
∴ স্তম্ভটির উচ্চতা 3√3 মিটার ।
Koshe Dekhi 25 Class 10|উচ্চতা ও দূরত্ব কষে দেখি ২৫ ক্লাস ১০
3. 150মি. লম্বা সুতো দিয়ে একটি মাঠ থেকে ঘুড়ি ওড়ানো হয়েছে ।ঘুড়িটি যদি অনুভূমিক রেখার সঙ্গে 60° কোণ করে উড়তে থাকে ,তাহলে ঘুড়িটি মাঠ থেকে কত উঁচুতে রয়েছে হিসাব করে লিখি ।
সমাধানঃ
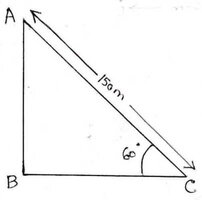
ধরাযাক , AB হল মাঠ থেকে ঘুড়িটির উচ্চতা । AC হল সুতোর দৈর্ঘ্য ।
∴ AC=150 মিটার । ∠ACB = 60°
এখন ABC ত্রিভুজে ∠ABC =90° এবং ∠ACB = 60°
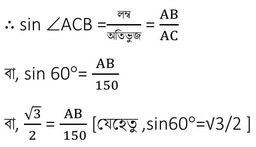
বা, AB = 150√3/2
বা, AB = 75√3
∴ মাঠ থেকে ঘুড়িটির উচ্চতা 75√3 মিটার ।
Koshe Dekhi 25 Class 10|উচ্চতা ও দূরত্ব কষে দেখি ২৫ ক্লাস ১০
4. একটি নদীর একটি পাড়ের একটি তালগাছের সোজাসুজি অপর পাড়ে একটি খুঁটি পুঁতলাম । এবার নদীর পাড় ধরে ওই খুঁটি থেকে 7√3 মিটার সরে গিয়ে দেকছি নদীর পাড়ের পরিপ্রেক্ষিতে গাছটির পাদদেশ 60° কোণে রয়েছে । নদীটি কত মিটার চওড়া হিসাব করে লিখি।
সমাধানঃ
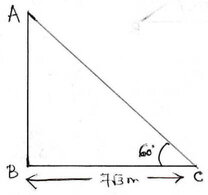
ধরাযাক , A বিন্দুতে গাছটির অবস্থান এবং B বিন্দুতে খুঁটি পোঁতা হয়েছে । এখন B বিন্দু থেকে 7√3 মিটার দূরে C বিন্দু থেকে গাছটির পাদদেশ অর্থাৎ A বিন্দু , 60° কোণে রয়েছে ।
∴ ∆ ABC ত্রিভুজে ∠ABC = 90° এবং BC =7√3 মিটার এবং ∠ACB=60°

বা, AB = 21
∴ নদীটি 21 মিটার চওড়া ।
Koshe Dekhi 25 Class 10|উচ্চতা ও দূরত্ব কষে দেখি ২৫ ক্লাস ১০
5. ঝরে একটি টেলিগ্রাফপোস্ট মাটি থেকে কিছু উপরে মচকে যাওয়ায় তার অগ্রভাগ গোড়া থেকে 8√3 মিটার দূরে মাটি স্পর্শ করেছে এবং অনুভূমিকরেখার সঙ্গে 30°কোণ উৎপন্ন করেছে।পোস্টটি মাটি থেকে কত উপরে মচকে ছিল এবং পোস্টটির উচ্চতা কত ছিল হিসাব করে লিখি।
সমাধানঃ
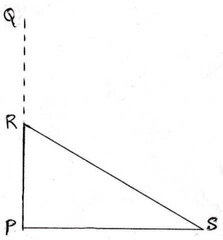
ধরাযাক , PQ টেলিগ্রাফ পোস্টটি R বিন্দুতে মচকে ছিল এবং মচকে যাওয়ার ফলে পোস্টটি 8√3 মিটার দূরে S বিন্দুতে মাটি স্পর্শ করেছে এবং অনুভূমিক রেখার সঙ্গে 30° কোণ উৎপন্ন করেছে । ∴ PS = 8√3 মিটার এবং PSR =30°
ধরি, পোস্টটি মাটি থেকে x মিটার উপরে ভেঙ্গেছিল । ∴ PR = x মিটার
এখন , PSR ত্রিভুজে RPS =90° এবং RSP =30°

∴ টেলিগ্রাফ পোস্টটি মাটি থেকে 8 মিটার উঁচুতে ভেঙ্গেছিল ।
আবার ত্রিভুজ PRS এর ক্ষেত্রে

বা, RS = 16
যেহেতু , RS = RQ
∴ RQ = 16 মিটার
∴ PQ = PR+RQ =(8+16) মিটার = 24 মিটার
∴ টেলিগ্রাফ পোস্টটির উচ্চতা 24 মিটার ।
Koshe Dekhi 25 Class 10|উচ্চতা ও দূরত্ব কষে দেখি ২৫ ক্লাস ১০
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
6. আমাদের পাড়ায় রাস্তার দুপাশে পরস্পর বিপরীত দিকে দুটি বাড়ি আছে । প্রথম বাড়ির দেওয়ালের গোড়া থেকে 6 মিটার দূরে একটি মইয়ের গোড়া রেখে যদি মইটিকে দেওয়ালে ঠেকানো যায় ,তবে তা অনুভূমিক রেখার সঙ্গে 30° কোণ উৎপন্ন করে ।কিন্তু মইটিকে যদি একই জায়গায় রেখে দ্বিতীয় বাড়ির দেওয়ালে লাগানো যায় ,তাহলে অনুভূমিক রেখার সঙ্গে 60° কোণ উৎপন্ন করে ।
(i) মইটির দৈর্ঘ্য নির্ণয় কর ।
(ii) দ্বিতীয় বাড়ির দেওয়ালের গোড়া থেকে মইটির গোড়া কত দূরে রয়েছে হিসাব করে লিখি ।
(iii) রাস্তাটি কত চওড়া নির্ণয় করি ।
(iv) দ্বিতীয় বাড়ির কত উঁচুতে মইটির অগ্রভাগ স্পর্শ করবে নির্ণয় করি ।
সমাধানঃ
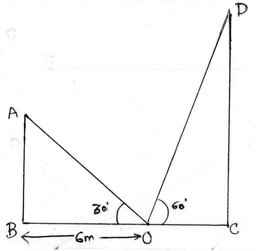
ধরাযাক , AB ও CD হল BC রাস্তার দুপাশে পরস্পর বিপরীত দিকে দুটি বাড়ি । B বিন্দু থেকে 6 মিটার দূরে O বিন্দু থেকে মইটিকে একটি বাড়ির দেওয়ালে ঠেকান হলে তা অনুভূমিক রেখার সঙ্গে 30° কোণ উৎপন্ন করে । ∴ ∠AOB =30°.
আবার ওই একই বিন্দু O থেকে মইটিকে অপর বাড়ির দেওয়ালে ঠেকালে তা অনুভূমিক রেখার সঙ্গে 60°কোণ উৎপন্ন করে ।
∴ ∠COD= 60°
(i) ধরাযাক , মইটির দৈর্ঘ্য x মিটার । ∴ OA =OD=x মিটার
এখন , ABO ত্রিভুজে ∠ABO =90° এবং ∠AOB =30°
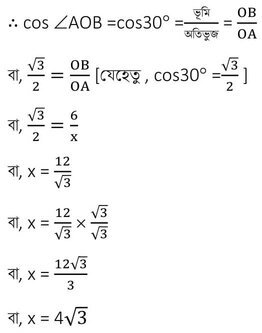
∴ মইটির দৈর্ঘ্য 4√3 মিটার ।
(ii) OCD ত্রিভুজে ∠OCD=90° এবং ∠COD = 60°

∴ দ্বিতীয় বাড়ির দেওয়ালের গোড়া থেকে মইয়ের গোড়া 2√3 মিটার দূরে রয়েছে ।
(iii) BC=OB+OC=6+2√3 =2(3+√3)
∴ রাস্তাটি 2(3+√3) মিটার চওড়া ।
(iv) ∠OCD ত্রিভুজে ∠OCD=90° এবং ∠COD = 60°

∴ দ্বিতীয় বাড়ির 6 মিটার উঁচুতে মইটির অগ্রভাগ স্পর্শ করবে ।
Koshe Dekhi 25 Class 10|উচ্চতা ও দূরত্ব কষে দেখি ২৫ ক্লাস ১০
7.যদি একটি চিমনির গোড়ার সঙ্গে সমতলে অবস্থিত একটি বিন্দুর সাপেক্ষে চিমনির চূড়ার উন্নতি কোণ 60° হয় এবং সেই বিন্দু ও চিমনির গোড়ার সঙ্গে একই সরলরেখায় অবস্থিত ওই বিন্দু থেকে আরও 24 মিটার দূরের অপর একটি বিন্দুর সাপেক্ষে চিমনির চূড়ার উন্নতি কোণ 30° হয় , তাহলে চিমনির উচ্চতা হিসাব করে লিখি । [√3-এর আসন্ন মান 1.732 ধরে তিন দশমিক স্থান পর্যন্ত আসন্ন মান নির্ণয় করি ]
সমাধানঃ
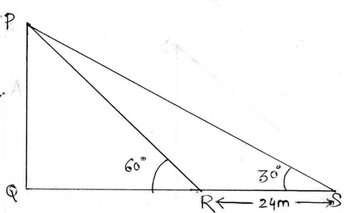
ধরাযাক , PQ চিমনির গোড়া অর্থাৎ Q বিন্দুর সঙ্গে একই সমতলে অবস্থিত R বিন্দুর সাপেক্ষে চিমনির চূড়ার উন্নতি কোণ 60°
∴ ∠QRP = 60°
আবার Q বিন্দুর সঙ্গে একই সমতলে অবস্থিত R বিন্দু থেকে 24 মিটার দূরে S বিন্দুর সাপেক্ষে চিমনির চূড়া অর্থাৎ P বিন্দুর উন্নতি কোণ 30° ।
∴ ∠QSP=30° এবং RS=24মিটার
এখন PQR ত্রিভুজে ∠PQR=90°এবং ∠PRQ = 60°


8. সূর্যের উন্নতি কোণ 45° থেকে বৃদ্ধি পেয়ে 60° হলে , একটি খুঁটির ছায়ার দৈর্ঘ্য 3 মিটার কমে যায় । খুঁটিটির উচ্চতা নির্ণয় করি । [√3-এর আসন্ন মান 1.732 ধরে তিন দশমিক স্থান পর্যন্ত আসন্ন মান নির্ণয় করি ]
সমাধানঃ
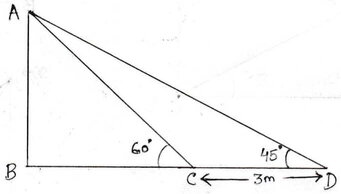
ধরাযাক , AB হল খুঁটির দৈর্ঘ্য । যখন সূর্যের উন্নতি কোণ 45° হলে খুঁটির ছায়ার দৈর্ঘ্য হয় BD এবং সূর্যের উন্নতি কোণ 60° হলে খুঁটির ছায়ার দৈর্ঘ্য হয় BC , অর্থাৎ খুঁটির ছায়ার দৈর্ঘ্য CD একক কমে যায় ।
∴ CD = 3 মিটার
ABC ত্রিভুজের ∠ABC=90° এবং ∠ACB =60°
এখন ABC সমকোণী ত্রিভুজ থেকে পাই ,

আবার ABD ত্রিভুজের ∠ABD=90° এবং ∠ADB =45°
ABD সমকোণী ত্রিভুজ থেকে পাই ,

9. 9√3 মিটার উঁচু তিনতলা বাড়ির ছাদ থেকে দেখলে 30মিটার দূরে অবস্থিত একটি কারখানার চিমনির উন্নতি কোণ 30° হয় । চিমনির উচ্চতা হিসাব করে লিখি ।
সমাধানঃ
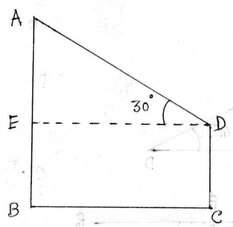
ধরাযাক ,চিমনির উচ্চতা AB এবং তিনতলা বাড়ির উচ্চতা CD । তিনতলা বাড়ির ছাদ অর্থাৎ D বিন্দু থেকে চিমনির চূড়া অর্থাৎ A বিন্দুর উন্নতি কোণ 30° । তিনতলা বাড়ির উচ্চতা 9√3 মিটার ∴ CD =9√3 মিটার
চিমনি ও তিনতলা বাড়ির দূরত্ব 30মিটার
∴ BC = 30 মিটার ।
এখন DE ⊥ AB অঙ্কন করা হল ।
∴ ∠ADE=30° এবং CD= BE=9√3 মিটার এবং BC=ED=30 মিটার
এখন, AED সমকোণী ত্রিভুজ থেকে পাই ,
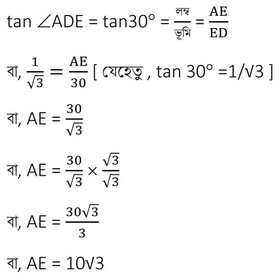
∴ চিমনির উচ্চতা AB =AE+EB = (10√3+9√3) মিটার = 19√3 মিটার ।
10. একটি লাইট হাউস থেকে তার সঙ্গে একই সরলরেখায় অবস্থিত দুটি জাহাজের মাস্তুলের গোড়ার অবনতি কোণ যথাক্রমে 60° ও 30° হয় এবং কাছের জাহাজের মাস্তুল যদি লাইট হাউস থেকে 150 মিটার দুরত্বে থাকে ,তাহলে দূরের জাহাজের মাস্তুল লাইট হাউস থেকে কত দূরত্বে রয়েছে এবং লাইট হাউসটির উচ্চতা হিসাব করে লিখি ।
সমাধানঃ
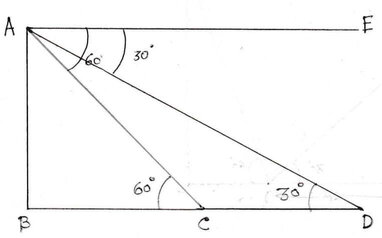
ধরাযাক , AB হল লাইট হাউসের উচ্চতা । A বিন্দু থেকে C বিন্দুতে এবং D বিন্দুতে অবস্থিত জাহাজের মাস্তুলের অবনতি কোণ যথাক্রমে 60° ও 30° । আবার লাইট হাউস থেকে কাছের জাহাজের দূরত্ব 150 মিটার ।
∴ BC =150 মিটার ।
AE || BD অঙ্কন করা হল
∴ ∠EAC = 60°এবং ∠EAD = 30°
আবার , ∠ACB = ∠EAC [একান্তর কোণ] এবং ∠EAD = ∠ADB [একান্তর কোণ ]
∴ ∠ACB =60° এবং ∠ADB = 30°
ABC ত্রিভুজে ∠ACB = 60° এবং ∠ABC = 90°
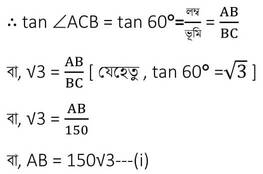
আবার , ABD ত্রিভুজে ∠ABD =90° এবং ∠ADB = 30°
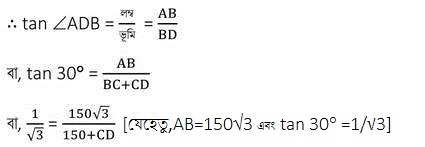
বা, 150+CD= 450
বা, CD = 300
∴ BD = BC+CD = 150+300=450মিটার
∴ লাইট হাউস থেকে দূরের জাহাজের দূরত্ব 450 মিটার এবং লাইট হাউসের উচ্চতা 150√3 মিটার।
11. একটি পাঁচতলা বাড়ির ছাদের কোনো বিন্দু থেকে দেখলে মনুমেন্টের চূড়ার উন্নতি কোণ ও গোড়ার অবনতি কোণ যথাক্রমে 60°এবং 30° ; বাড়িটির উচ্চতা 16 মিটার হলে , মনুমেন্টের উচ্চতা এবং বাড়িটি মনুমেন্ট থেকে কত দূরে অবস্থিত হিসাব করে লিখি ।
সমাধানঃ
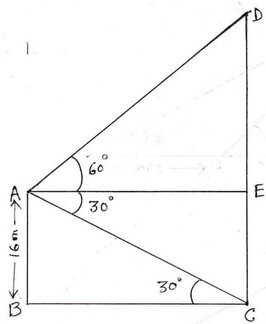
ধরাযাক , AB হল বাড়ির উচ্চতা এবং CD হল মনুমেন্টের উচ্চতা ।
∴ AB= 16 মিটার ।
বাড়ির ছাদ অর্থাৎ A বিন্দু থেকে মনুমেন্টের চূড়া অর্থাৎ D বিন্দুর উন্নতি কোণ 60 এবং মনুমেন্টের গোড়ার অর্থাৎ C বিন্দুর অবনতি কোণ 30° ।
∴ ∠DAE = 60°
এখন AE ⊥ CD অঙ্কন করা হল ।
∴ AE || BC
∴ ∠EAC =একান্তর কোণ∠ACB = 30°
যেহেতু , AE || BC এবং AB||EC এবং ∠ABC=∠BCE= 90°
∴ ABCE একটি আয়তক্ষেত্র ।
∴ AB =CE =16 মিটার এবং BC=AE
এখন , ABC ত্রিভুজে ∠ABC = 90° এবং ∠ACB = 30°
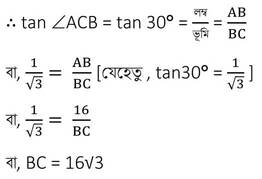
∴বাড়ি থেকে মনুমেন্টের দূরত্ব 16√3 মিটার ।
এখন , AED ত্রিভুজে ∠AED = 90° এবং ∠DAE =60°
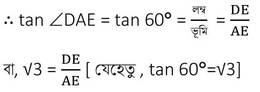
বা, DE = AE√3
বা, DE = 16√3 ✕√3 [ যেহেতু ,AE=BC]
বা, DE = 48
∴ মনুমেন্টের উচ্চতা = (DE+EC) = (48+16)মিটার = 64 মিটার ।
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
12. 250 মিটার লম্বা সুতো দিয়ে একটি ঘুড়ি ওড়াচ্ছি । সুতোটি যখন অনুভূমিক রেখার সঙ্গে 60° কোণ করে থাকে এবং সুতোটি যখন অনুভূমিক রেখার সঙ্গে 45° কোণ করে থাকে তখন প্রতি ক্ষেত্রে ঘুড়িটি আমার থেকে কত উপরে থাকবে হিসাব করে লিখি ।এদের মধ্যে কোন ক্ষেত্রে ঘুড়িটি বেশি উঁচুতে থাকবে নির্ণয় করি ।
সমাধানঃ
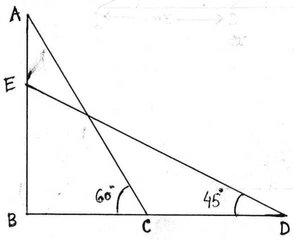
ধরাযাক , যখন ঘুড়ির সুতো অনুভূমিক রেখার সঙ্গে 60° কোণ করে তখন ঘুড়ির উচ্চতা AB আবার যখন ঘুড়ির সুতো অনুভূমিক রেখার সঙ্গে 45° কোণ করে তখন ঘুড়ির উচ্চতা EB । প্রতিক্ষেত্রে সুতোর দৈর্ঘ্য 250 মিটার । ∴ DE=AC=250মিটার
এখন , ABC ত্রিভুজে ∠ABC =90° এবং ∠ACB = 60°
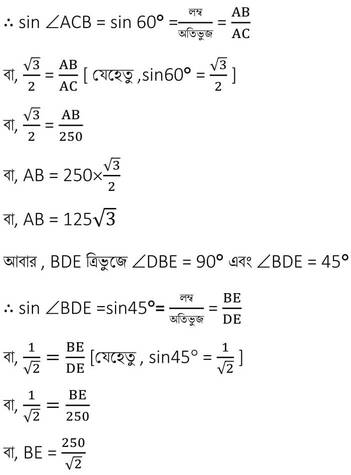
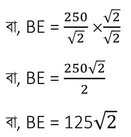
∴ যখন ঘুড়ির সুতো অনুভূমিক রেখার সঙ্গে 60° কোণ করে তখন ঘুড়ির উচ্চতা হবে 125√3 মিটার ।
আবার যখন যখন ঘুড়ির সুতো অনুভূমিক রেখার সঙ্গে 45° কোণ করে তখন ঘুড়ির উচ্চতা হবে 125√2 মিটার ।
অর্থাৎ এদের মধ্যে যেহেতু 125√3 মিটার দৈর্ঘ্যটি বড় , ∴ যখন ঘুড়ির সুতো অনুভূমিক রেখার সঙ্গে 60° কোণ করে তখন ঘুড়ির উচ্চতা বেশি হবে ।
Koshe Dekhi 25 Class 10|উচ্চতা ও দূরত্ব কষে দেখি ২৫ ক্লাস ১০
13. উড়োজাহাজের একজন যাত্রী কোনো এক সময় তাঁর এক পাশে হাওড়া স্টেশনটি এবং তাঁর ঠিক বিপরীত পাশে শহিদ মিনারটি যথাক্রমে 60° ও 30° অবনতি কোণে দেখতে পান । ওই সময় উড়োজাহাজটি যদি ঠিক 545√3 মিটার উঁচুতে থাকে ,তাহলে হাওড়া স্টেশন ও শহিদ মিনারের দূরত্ব নির্ণয় করি ।
সমাধানঃ
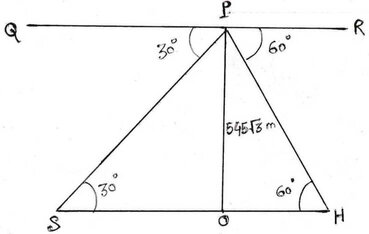
ধরাযাক ,H ,S এবং P যথাক্রমে হাওড়া স্টেশন , শহিদ মিনার এবং উড়োজাহাজের অবস্থান ।
∴ P বিন্দু থেকে H বিন্দুর অবনতি কোণ 60° এবং P বিন্দু থেকে S বিন্দুর অবনতি কোণ 30° এবং মাটি থেকে উড়োজাহাজটির উচ্চতা OP = 545√3 মিটার ।
এখন , P বিন্দু দিয়ে SH সরলরেখার সমন্তরাল সরলরেখা QR টানা হল
∴ ∠QPS = 30° এবং ∠RPH = 60°
∴ ∠QPS =একান্তর কোণ∠PSO = 30°
এবং ∠RPH =একান্তর কোণ∠PHO = 60°
এখন , PSO ত্রিভুজে ∠POS=90°এবং ∠PSO = 30°

∴ SH = SO+OH = (1635+545)মিটার = 2180 মিটার
∴ হাওড়া স্টেশন থেকে শহিদ মিনারের দূরত্ব 2180 মিটার ।
Koshe Dekhi 25 Class 10|উচ্চতা ও দূরত্ব কষে দেখি ২৫ ক্লাস ১০
14.একটি তিনতলা বাড়ির ছাদে 3.3 মিটার দৈর্ঘ্যের একটি পতাকা আছে । রাস্তার কোনো এক স্থান থেকে দেখলে পতাকা দণ্ডটির চূড়া ও পাদদেশের উন্নতি কোণ যথাক্রমে 50° ও 45° হয় । তিনতলা বাড়ির উচ্চতা হিসাব করে লিখি ।
সমাধানঃ
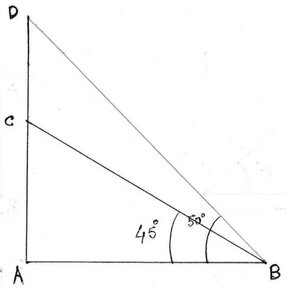
AC হল তিনতলা বাড়ির উচ্চতা এবং CD হল পতাকার দৈর্ঘ্য ।রাস্তার উপর একটি বিন্দু B থেকে পতাকার পাদদেশের অর্থাৎ C বিন্দুর উন্নতি কোণ 45° এবং B বিন্দু থেকে পতাকার চূড়া অর্থাৎ D বিন্দুর উন্নতি কোণ 50°।
∴CD =3.3 এবং ∠ABC = 45° এবং ∠ABD = 50°
এখন , ABC ত্রিভুজে ∠BAC =90° এবং ∠ABC =45°

বা, AC = 17.188
বা, AC = 17.19(প্রায়)
∴ তিনতলা বাড়ির উচ্চতা 17.19 মিটার প্রায় ।
Koshe Dekhi 25 Class 10|উচ্চতা ও দূরত্ব কষে দেখি ২৫ ক্লাস ১০
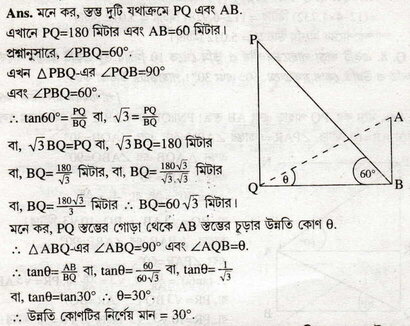
15. দুটি স্তম্ভের উচ্চতা যথাক্রমে 180 মিটার ও 60 মিটার।দ্বিতীয় স্তম্ভটির গোড়া থেকে প্রথমটির চূড়ার উন্নতি কোণ 60° হলে ,প্রথমটির গোড়া থেকে দ্বিতীয়টির চূড়ার উন্নতি কোণ হিসাব করে লিখি।
16. সূর্যের উন্নতি কোণ 45° হলে কোনো সমতলে অবস্থিত একটি স্তম্ভের ছায়ার দৈর্ঘ্য যা হয় , উন্নতি কোণ 30° হলে ছায়ার দৈর্ঘ্য তার চেয়ে 60 মিটার বেশি হয় । স্তম্ভটির উচ্চতা নির্ণয় করি ।
সমাধানঃ
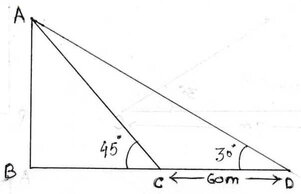
ধরাযাক , AB হল স্তম্ভের দৈর্ঘ্য । যখন সূর্যের উন্নতি কোণ 45° তখন AB স্তম্ভের ছায়ার দৈর্ঘ্য হয় BC এবং সূর্যের উন্নতি কোণ যখন 30° তখন ছায়ার দৈর্ঘ্য CD=60 মিটার বৃদ্ধি পায় এবং ছায়ার দৈর্ঘ্য হয় BD
∴ BD = BC+CD = (BC+60)মিটার
ABC ত্রিভুজের ∠ABC =90° এবং ∠ACB = 45°
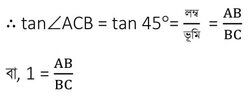
বা, AB = BC —(i)
ABD ত্রিভুজের ∠ABD =90° এবং ∠ADB = 30°

বা, AB = 30(√3+1)=30(1.732+1)=30✕ 2.732 =81.96
∴ AB=81.96 মিটার (প্রায়)
∴ স্তম্ভের দৈর্ঘ্য 81.96 মিটার (প্রায়) ।
Koshe Dekhi 25 Class 10|উচ্চতা ও দূরত্ব কষে দেখি ২৫ ক্লাস ১০
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
17. একটি চিমনির সঙ্গে একই সমতলে অবস্থিত অনুভূমিক সরলরেখায় কোনো বিন্দু থেকে চিমনির দিকে 50 মিটার এগিয়ে যাওয়ায় তার চূড়ার উন্নতি কোণ 30°থেকে 60° হল । চিমনির উচ্চতা হিসাব করে লিখি।
সমাধানঃ
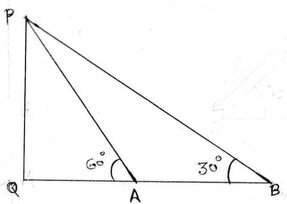
ধরাযাক , PQ চিমনির পাদদেশের সঙ্গে একই সমতলে অবস্থিত অনুভূমিক সরলরেখার B এবং A বিন্দু থেকে চিমনির চূড়ার উন্নতি কোণ যথাক্রমে 30° এবং 60° ; অর্থাৎ AB=50 মিটার ।
এখন PAQ ত্রিভুজের ∠PQA =90 এবং ∠PAQ =60

Koshe Dekhi 25 Class 10|উচ্চতা ও দূরত্ব কষে দেখি ২৫ ক্লাস ১০
18. 126 ডেসিমি. উঁচু একটি উল্লম্ব খুঁটি মাটি থেকে কিছু উপরে দুমড়ে গিয়ে উপরের অংশ কাত হয়ে পড়ায় তার অগ্রভাগ মাটি স্পর্শ করে ভূমির সঙ্গে 30° কোণ উৎপন্ন করেছে । খুঁটিটি কত উপরে দুমড়ে গিয়েছিল এবং তার অগ্রভাগ গোড়া থেকে কত দূরে মাটি স্পর্শ করেছিল হিসাব করে লিখি ।
সমাধানঃ
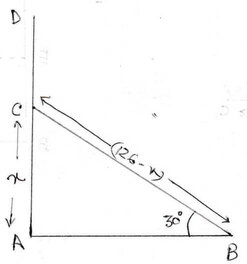
ধরাযাক, AD খুঁটি x ডেসিমি. উচ্চতায় C বিন্দুতে মচকে গিয়েছিল । ∴ AD=126 ডেসিমি. এবং AC=x ডেসিমি.
∴ CD=BC=(126-x)ডেসিমি.
এখন ABC ত্রিভুজে ∠BAC =90° এবং ∠ABC =30°
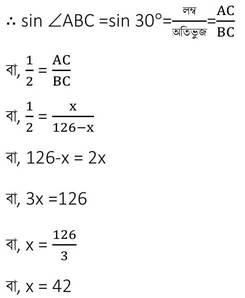
∴ খুঁটিটি মাটি থেকে 42 ডেসিমি. উঁচুতে ভেঙ্গেছিল ।
আবার ABC সমকোণী ত্রিভুজ থেকে পাই ,

বা, AB = 42√3
∴ খুঁটিটির অগ্রভাগ 42√3 ডেসিমিটার দূরে মাটি স্পর্শ করেছিল ।
19. মাঠের মাঝখানে দাঁড়িয়ে মোহিত একটি উড়ন্ত পাখিকে প্রথমে উত্তরদিকে 30° উন্নতি কোণে এবং 2 মিনিট পর দক্ষিন দিকে 60° উন্নতি কোণে দেখতে পেল । পাখিটি যদি একই সরলরেখা বরাবর 50√3 মিটার উঁচুতে উড়ে থাকে ,তবে তার গতিবেগ কিলোমিটার প্রতি ঘণ্টায় নির্ণয় করি ।
সমাধানঃ
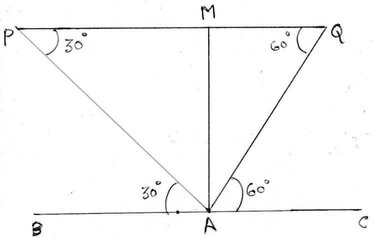
ধরি , মোহিত BC মাঠের A বিন্দুতে দাঁড়িয়ে পাখিটিকে প্রথমে P বিন্দুতে 30° উন্নতি কোণে এবং 2 মিনিট পরে Q বিন্দুতে 60° উন্নতি কোণে দেখে । যেহেতু পাখিটি একই সরলরেখায় উড়ছিল ,তাই PQ || BC ও A বিন্দু থেকে পাখিটির উচ্চতা AM = 50√3 মিটার
এখন, ∠APM = একন্তর ∠BAP = 30° [যেহেতু,PQ||BC]
এবং , ∠AQM = একান্তর∠QAC = 60° [যেহেতু,PQ||BC]
সমকোণী ত্রিভুজ APM থেকে পাই ,

সমকোণী ত্রিভুজ AMQ থেকে পাই

∴ PQ =PM+MQ =(150+50)মিটার = 200 মিটার

Madhyamik Math Koshe Dekhi 25|উচ্চতা ও দূরত্ব কষে দেখি ২৫ ক্লাস ১০|Koshe Dekhi 25 Class 10
20. 5√3 মিটার উঁচু রেলওয়ে ব্রিজে দাঁড়িয়ে অমিতাদিদি প্রথমে একটি ট্রেনের ইঞ্জিনকে ব্রিজের এপারে 30° অবনতি কোণে দেখলেন । কিন্তু 2 সেকেন্ড পরই ওই ইঞ্জিনকে ব্রিজের ওপারে 45° অবনতি কোণে দেখলেন । ট্রেনটির গতিবেগ মিটার প্রতি সেকেন্ডে হিসাব করে লিখি ।
সমাধানঃ
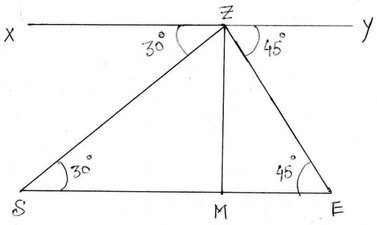
ধরি ,অমিতাদিদি XY রেলওয়ে ওভারব্রিজের Z বিন্দুতে দাঁড়িয়ে ট্রেনের ইঞ্জিনকে প্রথমে S বিন্দুতে এবং 2 সেকেন্ড পরে E বিন্দুতে দেখলেন । অবনতি কোণ ∠XZS =30° এবং ∠YZE =45°
ZM = রেলওয়ে ওভারব্রিজের উচ্চতা = 5√3 মিটার
আবার যেহেতু XY||SE
∴ ∠ZSM = একান্তর ∠XZS = 30°
এবং ∠ZEM = একান্তর ∠YZE =45°
সমকোণী ত্রিভুজ ZSM থেকে পাই

সমকোণী ত্রিভুজ ZEM থেকে পাই
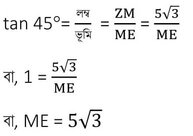
∴ SE = SM+ME =(15+5√3)=15+5✕1.732 =15+8.660=23.660

Koshe Dekhi 25 Class 10|উচ্চতা ও দূরত্ব কষে দেখি ২৫ ক্লাস ১০
21.একটি নদীর পাড়ের সঙ্গে লম্বভাবে একটি সেতু আছে ।সেতুটির একটি পাড়ের প্রান্ত থেকে নদীর পাড় ধরে কিছু দূর গেলে সেতুর অপর প্রান্তটি 45° কোণে এবং পাড় ধরে আরও 400 মিটার দূরে সরে গেলে সেই প্রান্তটি 30° কোণে দেখা যায় । সেতুটির দৈর্ঘ্য নির্ণয় করি ।
সমাধানঃ
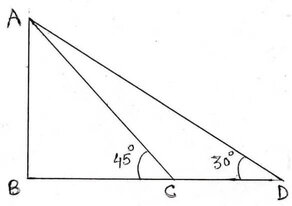
ধরি , নদীর পাড়ের সঙ্গে লম্ব ভাবে অবস্থিত একটি সেতু হল AB এবং তার B প্রান্ত থেকে কিছু দূরে C বিন্দু থেকে সেতুর অপর প্রান্ত A বিন্দুর সাপেক্ষে উৎপন্ন কোণ ∠BCA =45° এবং C বিন্দু থেকে আরও 400 মিটার দূরে D বিন্দু থেকে A বিন্দুর সাপেক্ষে উৎপন্ন কোণ ∠BDA =30° এবং CD=400 মিটার ।
সমকোণী ত্রিভুজ ABC থেকে পাই ,

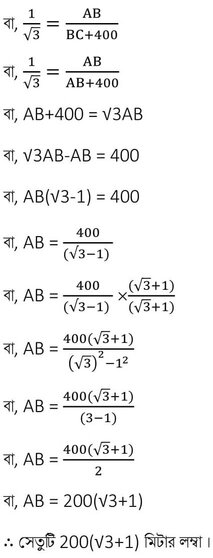
Koshe Dekhi 25 Class 10|উচ্চতা ও দূরত্ব কষে দেখি ২৫ ক্লাস ১০
22. একটি পার্কের একপ্রান্তে অবস্থিত 15 মিটার উঁচু একটি বাড়ির ছাদ থেকে পার্কের অপর পাড়ে অবস্থিত একটি ইটভাটার চিমনির পাদদেশ ও অগ্রভাগ যথাক্রমে 30° অবনতি কোণ এবং 60° উন্নতি কোণে দেখা যায় । ইটভাটার চিমনির উচ্চতা এবং ইটভাটা ও বাড়ির মধ্যে দূরত্ব নির্ণয় করি
সমাধানঃ
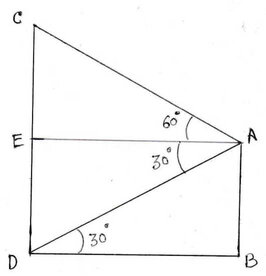
ধরি , AB একটি 15 মিটার উঁচু বাড়ি এবং CD ইটভাটার চিমনি । বাড়ির ছাদ A থেকে চিমনির পাদদেশ D এর অবনতি কোণ এবং অগ্রভাগ C এর উন্নতি কোণ যথাক্রমে 30° এবং 60°
A বিন্দু থেকে BD এর সমান্তরাল সরলরেখা CD কে E বিন্দুতে ছেদ করে । যেহেতু AE ||BD
∴ ∠ADB = একান্তর ∠EAD =30°
সমকোণী ত্রিভুজ ABD থেকে পাই ,
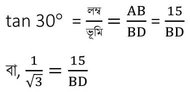
বা, BD = 15√3
∴ ইট ভাটা ও বাড়ির মধ্যে দূরত্ব 15√3 মিটার ।
আবার , AE=BD = 15√3
সমকোণী ত্রিভুজ AEC থেকে পাই ,

বা, CE = 45
∴ CD = CE+ED= CE+AB = 45+15=60
∴ চিমনির উচ্চতা 60 মিটার ।
23. একটি উড়োজাহাজ থেকে রাস্তায় পরপর দুটি কিলোমিটার ফলকের অবনতি কোণ যথাক্রমে 60° ও 30° হলে, উড়োজাহাজটির উচ্চতা নির্ণয় করি , (i) যখন ফলক দুটি উড়োজাহাজের বিপরীত পাশে অবস্থিত (ii) যখন ফলক দুটি উড়োজাহাজের একই পাশে আছে ।
সমাধানঃ (i)
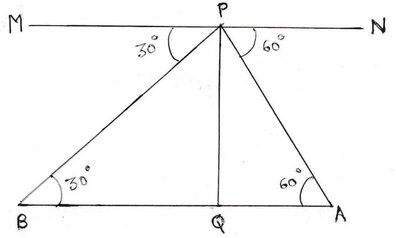
ধরাযাক , P উড়োজাহাজটির অবস্থান এবং A ও B যথাক্রমে সোজা রাস্তার উপর P –এর বিপরীত দিকে পরপর দুটি কিলোমিটার ফলক । অর্থাৎ AB =1 কিলোমিটার ।
আবার , P থেকে কিলোমিটার ফলক দুটির অবনতি কোণ জথক্রমে 60° ও 30° .
∴ ∠APN=60° এবং ∠BPM = 30°
PQ ⊥AB অঙ্কন করা হল ।
এখন MN || AB ,∴ ∠PAQ = একান্তর ∠APN =60° এবং ∠PBQ = একান্তর ∠BPM=30°
∴ ∆APQ এর ∠AQP =90° এবং ∠PAQ =60°

মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
(ii)
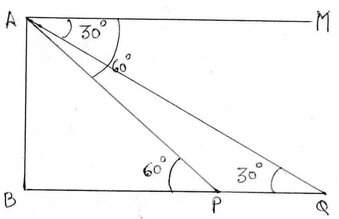
ধরি ,যখন উড়োজাহাজটির অবস্থান A বিন্দুতে ছিল তখন পরস্পর দুটি কিলোমিটার ফলক P এবং Q এর অবনতি কোণ যথাক্রমে 60° ও 30° ছিল এবং উড়োজাহাজটি AB উচ্চতায় উড়ছিল ।
ধরি , AM||BQ
∴ ∠MAP = 60° এবং ∠MAQ =30°
∠APB = একান্তর কোণ ∠MAP = 60°
এবং ∠AQB = একান্তর কোণ ∠MAQ = 30°
এক্ষেত্রে PQ = 1কিমি.
সমকোণী ত্রিভুজ APB থেকে পাই

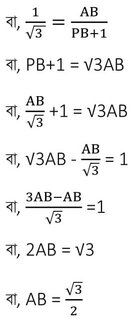
∴ AB = √3/2 কিমি. =(√3/2✕ 1000)মিটার =500√3 মিটার
সুতরাং রাস্তা থেকে উড়োজাহাজের উচ্চতা 500√3 মিটার ।
24.অতিসংক্ষিপ্ত উত্তধর্মী প্রশ্ন (M.C.Q.)
(i) মাঠের উপর একটি বিন্দু থেকে মোবাইল টাওয়ারের চূড়ার উন্নতি কোণ 60 এবং টাওয়ারের গোড়া থেকে ওই বিন্দুর দূরত্ব 10 মিটার । টাওয়ারের উচ্চতা
(a) 10 মিটার
(b) 10√3 মিটার
(c) 10/√3 মিটার
(d) 100 মিটার
Ans: (b) 10√3 মিটার
সমাধানঃ
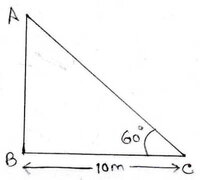
ধরি , AB হল টাওয়ারের উচ্চতা এবং মাঠের উপর C বিন্দু থেকে টাওয়ারের চূড়ার উন্নতি কোণ 60°
∴ ∠ACB =60°
এবং BC = 10 মিটার
ABC ত্রিভুজের ∠ABC =90° এবং ∠ACB = 60°
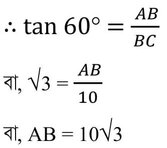
∴ টাওয়ারের উচ্চতা 10√3 মিটার ।
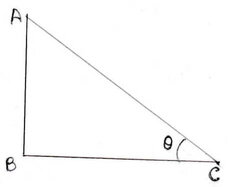
(ii) ϴ এর মান
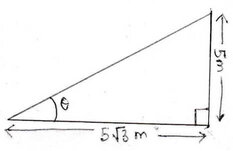
(a) 30°
(b) 45°
(c) 60°
(d) 75°
Ans:(a) 30°
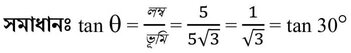
∴ ϴ=30°
Koshe Dekhi 25 Class 10|উচ্চতা ও দূরত্ব কষে দেখি ২৫ ক্লাস ১০
(iii) তিনতলা বাড়ির ছাদ থেকে মাটিতে পড়ে থাকা একটি বাক্সকে যত কোণে দেখলে বাড়ির উচ্চতা ও বাড়ি থেকে বাক্সটির দূরত্ব সমান হয় তা হল
(a) 15°
(b) 30°
(c ) 45°
(d) 60°
Ans: (c ) 45°
সমাধানঃ
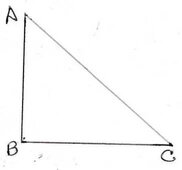
ধরাযাক , AB হল তিনতলা বাড়ি । C হল বাক্সের অবস্থান ।
ধরি , ছাদ A থেকে বাক্সকে ϴ কোণে দেখলে বাড়ির উচ্চতা এবং বাড়ি থেকে বাক্সের দূরত্ব সমান হয় ।
∴ AB = BC
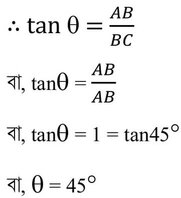
(iv) একটি টাওয়ারের উচ্চতা 100√3 মিটার । টাওয়ারের পাদবিন্দু থেকে 100 মিটার দূরে একটি বিন্দু থেকে টাওয়ারের চূড়ার উন্নতি কোণ
(a) 30°
(b) 45°
(c ) 60°
(d) কোনোটিই নয়
Ans: (c ) 60°
সমাধানঃ
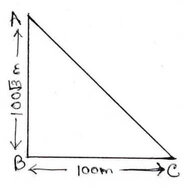
ধরাযাক, AB হল টাওয়ারের উচ্চতা । ∴ AB = 100√3
ধরি , AB টাওয়ারের পাদবিন্দু থেকে 100 মিটার দূরের একটি বিন্দু C থেকে টাওয়ারের চূড়ার উন্নতি কোণ ϴ
∴ ∠ACB =ϴ এবং BC = 100 মিটার
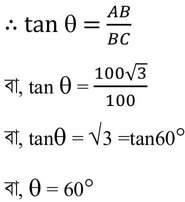
∴ টাওয়ারের চূড়ার উন্নতি কোণ 60°
(v) একটি পোস্টের ভূমিতলের ছায়ার দৈর্ঘ্য পোস্টের উচ্চতার √3 গুন হলে, সূর্যের উন্নতি কোণ
(a) 30°
(b) 45°
(c ) 60°
(d) কোনোটিই নয়
Ans: (a) 30°
সমাধানঃ
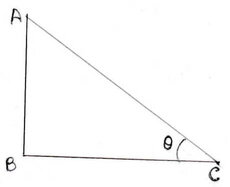
ধরাযাক , পোস্টটির উচ্চতা AB এবং পোস্টের ছায়ার দৈর্ঘ্য BC এবং সূর্যের উন্নতি কোণ ϴ
∴ BC = √3 AB
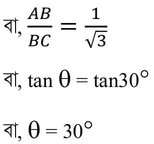
Madhyamik Math Koshe Dekhi 25|উচ্চতা ও দূরত্ব কষে দেখি ২৫ ক্লাস ১০|Koshe Dekhi 25 Class 10
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
(B) নীচের বিবৃতি গুলি সত্যি না মিথ্যা লিখিঃ
(i) ABC এর ∠B=90° , AB=BC হলে ∠C =60°
উত্তরঃ মিথ্যা
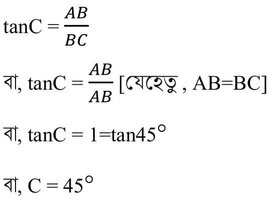
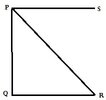
(ii) PQ একটি বাড়ির উচ্চতা , QR ভূমি । P থেকে R বিন্দুর অবনতি কোণ ∠SPR ; সুতরাং ∠SPR =∠PRQ
উত্তরঃ সত্য ।
যেহেতু , PS || QR এবং PR ভেদক
∴ ∠SPR = ∠PRQ [একান্তর কোণ]
(C ) শূন্যস্থান পূরণ করিঃ
(i) সূর্যের উন্নতি কোণ 30° থেকে বৃদ্ধি পেয়ে 60° হলে , একটি পোস্টের ছায়ার দৈর্ঘ্য __________ পায় । (বৃদ্ধি / হ্রাস )
উত্তরঃ হ্রাস পাবে ।
(ii) সূর্যের উন্নতি কোণ 45° হলে , একটি পোস্টের দৈর্ঘ্য ও তার ছায়ার দৈর্ঘ্য _________ হবে ।
উত্তরঃ সমান হবে ।
(iii) যখন সূর্যের উন্নতি কোণ 45° –এর _____________ তখন একটি স্তম্ভের ছায়ার দৈর্ঘ্য স্তম্ভের উচ্চতা থেকে কম ।
উত্তরঃ বেশি
25. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.):
(i) একটি ঘুড়ির উন্নতি কোণ 60° এবং সুতোর দৈর্ঘ্য 20√3 মিটার হলে, ঘুড়িটি মাটি থেকে কত উচ্চতায় আছে হিসাব করে লিখি ।
সমাধানঃ
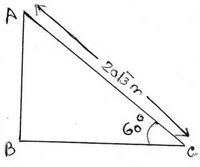
ধরাযাক, AB হল মাটি থেকে ঘুড়ির উচ্চতা । C বিন্দু থেকে A বিন্দুতে ঘুড়ির উন্নতি কোণ 60° এবং AC সুতোর দৈর্ঘ্য 20√3 মিটার ।
ABC ত্রিভুজের ∠ABC =90° এবং ∠ACB =60°
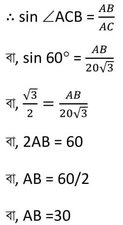
∴মাটি থেকে ঘুড়িটির উচ্চতা 30 মিটার ।
(ii) একটি সমকোণী ত্রিভুজাকারক্ষেত্র ABC –এর অতিভুজ AC এর দৈর্ঘ্য 100 মিটার এবং AB =50√3 মিটার হলে , ∠C এর মান নির্ণয় করি ।
সমাধানঃ
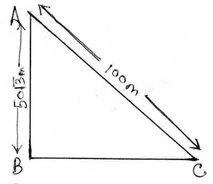
ABC সমকোণী ত্রিভুজে , C কোণের সাপেক্ষে AB হল লম্ব এবং AC হল অতিভুজ ।
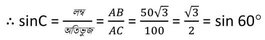
বা, sin∠C =sin60°
বা, ∠C = 60°
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
(iii) ঝরে একটি গাছ মচকে গিয়ে তার অগ্রভাগ এমনভাবে ভূমি স্পর্শ করেছে যে গাছটির অগ্রভাগ থেকে গোড়ার দূরত্ব এবং বর্তমান উচ্চতা সমান । গাছটির অগ্রভাগ ভূমির সাথে কত কোণ করেছে হিসাব করে লিখি ।
সমাধানঃ
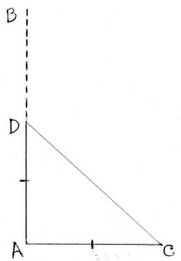
ধরাযাক , AB গাছটি ঝরে D বিন্দুতে মচকে গিয়ে গাছটির অগ্রভাগ C বিন্দুতে ভূমি স্পর্শ করেছে ।
প্রশ্নানুসারে , AD =AC
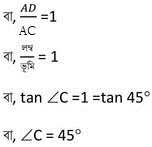
∴গাছটির ভূমির অগ্রভাগ ভূমির সাথে 45° কোণ করেছে ।
(iv) ABC সমকোণী ত্রিভুজে B =90°, AB –এর উপর D এমন বিন্দু যে AB:BC:BD = √3 :1:1 , ∠ACD –এর মান কত হিসাব করে লিখি ।
সমাধানঃ
ধরি , AB ,BC এবং BD –এর দৈর্ঘ্য যথাক্রমে √3x একক , x একক এবং x একক
ত্রিভুজ ABC এর , ∠ABC =90°

∴ ∠ACD = ∠ ACB – ∠ DCB = 60°-45° =15°
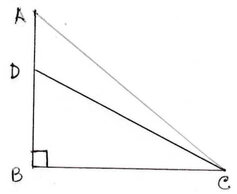
(v) একটি স্তম্ভের ছায়ার দৈর্ঘ্য এবং স্তম্ভের উচ্চতার অনুপাত √3 :1 হলে , সূর্যের উন্নতি কোণ নির্ণয় করি ।
সমাধানঃ
ধরি , AB স্তম্ভের ছায়ার দৈর্ঘ্য BC যখন সূর্যের উন্নতি কোণ ϴ ।
এখন ABC ত্রিভুজের ∠ABC =90°
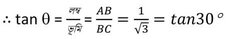
বা, ϴ=30° ∴ সূর্যের উন্নতি কোণ 30°
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
ধন্যবাদ । এই পোস্টটি ভাল লাগলে SHARE করার অনুরোধ রইল । এরকম আরও সুন্দর সুন্দর পোস্ট পেতে , আমাদের FACEBOOK PAGE টি LIKE করুন ।
Thanks ♥️♥️