Koshe Dekhi 3.1 & 3.2 Class 10| বৃত্ত সম্পর্কিত উপপাদ্য কষে দেখি ৩.১।বৃত্ত সম্পর্কিত উপপাদ্য কষে দেখি ৩.২।Koshe Dekhi 3.1 Class 10| Koshe Dekhi 3.2 Class 10|WBBSE Class 10(Ten)(X) Math Solution Of Chapter 3| Ganit Prakash Class 10 Chapter 3 Solution|WB Board Class 10 Math Solution In Bengali.
Koshe Dekhi 3.1 & 3.2 Class 10|বৃত্ত সম্পর্কিত উপপাদ্য কষে দেখি ৩.১ এবং কষে দেখি ৩.২|কষে দেখি 3.1 ক্লাস 10|কষে দেখি 3.2 ক্লাস 10
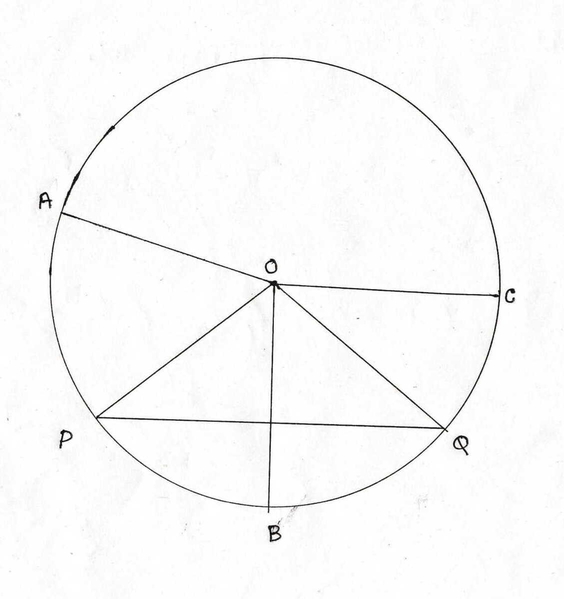
1. পাশে O কেন্দ্রিয় বৃত্তের ছবি দেখি এবং কোন কোন ব্যাসার্ধ PAQ বৃত্তাংশে অবস্থিত লিখি ।
উত্তরঃ
ও কেন্দ্রীয় বৃত্তের PAQ বৃত্তাংশে অবস্থিত ব্যাসার্ধ গুলি হলো OP, OA, OC, OQ ।
2. নীচের _____ এ বুঝে লিখি ।
(i) একটি বৃত্তে ____________ বিন্দু আছে ।
উত্তরঃ অসংখ্য
(ii) বৃত্তের বৃহত্তম জ্যা _________ ।
উত্তরঃ ব্যাস
(iii) জ্যা বৃত্তাকার ক্ষেত্র কে দুটি _________ এ বিভক্ত করে ।
উত্তরঃ বৃত্তাংশে
(iv) বৃত্তের সকল ব্যাস ____________ বিন্দুগামী ।
উত্তরঃ কেন্দ্রগামী
(v) দুটি বৃত্তাংশ সমান হলে তাদের বৃত্তচাপ দুটির দৈর্ঘ্য _________ হবে ।
উত্তরঃ দুটি বৃত্তাংশ সমান হলে তাদের বৃত্তচাপ দুটির দৈর্ঘ্য সমান হবে
(vi) একটি বৃত্তাকার ক্ষেত্রের বৃত্তকলা হলো বৃত্তচাপ এবং দুটি _________ এর দ্বারা সীমাবদ্ধ অঞ্চল ।
উত্তরঃ একটি বৃত্তাকার ক্ষেত্রের বৃত্তকলা হলো বৃত্তচাপ এবং দুটি ব্যাসার্ধের দ্বারা সীমাবদ্ধ অঞ্চল ।
(vii) বৃত্তের বাইরে কোনও বিন্দু ও কেন্দ্রের সংযোজক রেখাংশের দৈর্ঘ্য ব্যাসার্ধের দৈর্ঘ্য অপেক্ষা _________ ।
উত্তরঃ বৃত্তের বাইরে কোনও বিন্দু ও কেন্দ্রের সংযোজক রেখাংশের দৈর্ঘ্য ব্যাসার্ধের দৈর্ঘ্য অপেক্ষা বড় ।
3. স্কেল ও পেনসিল এর সাহায্যে একটি বৃত্ত এঁকে কেন্দ্র , জ্যা , ব্যাস , ব্যাসার্ধ , উপচাপ ,অধিচাপ , নির্দেশ করি ।
উত্তরঃ
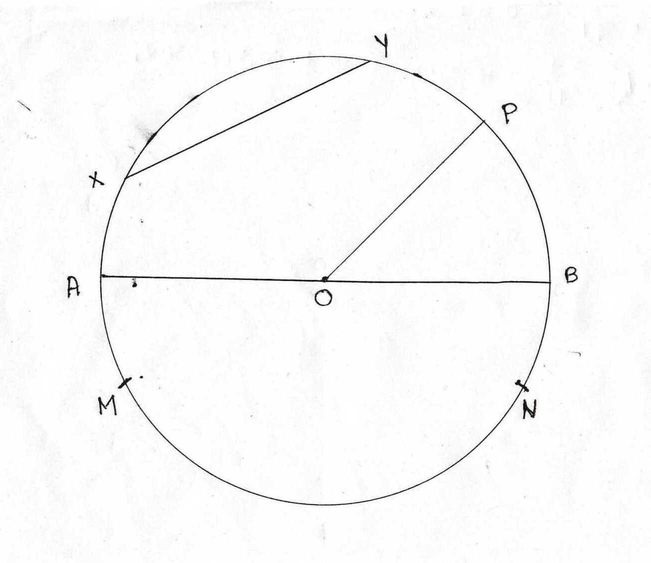
কেন্দ্র – O
জ্যা – XY
ব্যাস- AB
ব্যাসার্ধ- OP
উপচাপ- MN
অধিচাপ- AMNP
4. সত্য না মিথ্যা লিখি ঃ
(i) বৃত্ত একটি সামতলিক চিত্র ।
উত্তরঃ সত্য ।
(ii) বৃত্তাংশ (segment) একটি সামতলিক চিত্র ।
উত্তরঃ সত্য ।
(iii) বৃত্তকলা একটি সামতলিক চিত্র ।
উত্তরঃ সত্য ।
(iv) জ্যা একটি সরলরেখা ।
উত্তরঃ সত্য ।
(v) চাপ একটি সরলরেখা ।
উত্তরঃ মিথ্যা ।
(vi) একটি বৃত্তের সসীম সংখ্যক একই দৈর্ঘ্যের জ্যা আছে ।
উত্তরঃ মিথ্যা ।
(vii) একটি নির্দিষ্ট বিন্দুকে কেন্দ্র করে একটিই বৃত্ত আঁকা সম্ভব ।
উত্তরঃ মিথ্যা ।
(viii) দুটি সর্বসম বৃত্তের ব্যাসার্ধের দৈর্ঘ্য সমান ।
উত্তরঃ সত্য ।
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
কষে দেখি-3.2
Madhyamik Math koshe dekhi 3.1 And 3.2
1. O কেন্দ্রীয় বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি এবং AB একটি জ্যা এর দৈর্ঘ্য 8 সেমি । O বিন্দু থেকে AB জ্যা এর দূরত্ব হিসাব করে লিখি ।
সমাধানঃ
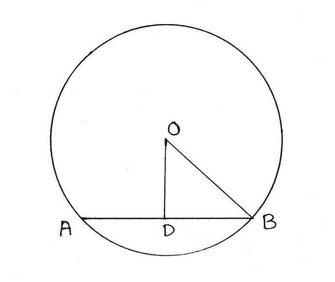
যেহেতু বৃত্তের কেন্দ্রগামী কোনও জ্যা এর ওপর অঙ্কিত লম্ব জ্যা টিকে সমদ্বিখন্ডিত করে ।
∴ D , AB মধ্যবিন্দু ।
∴ BD = AB/2= 8/2 = 4 সেমি
OB= বৃত্তের ব্যাসার্ধ = 5 সেমি ।
সমকোণী ত্রিভুজ ∆ OBD থেকে পাই ,
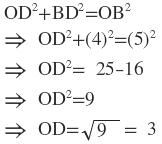
∴ o থেকে AB বিন্দুর দূরত্ব = 3 সেমি ।
2. O কেন্দ্রীয় একটি বৃত্তের ব্যাসের দৈর্ঘ্য 26 সেমি । O বিন্দু থেকে PQ জ্যা-এর দূরত্ব 5 সেমি । PQ জ্যা এর দৈর্ঘ্য হিসাব করে লিখি ।
সমাধানঃ
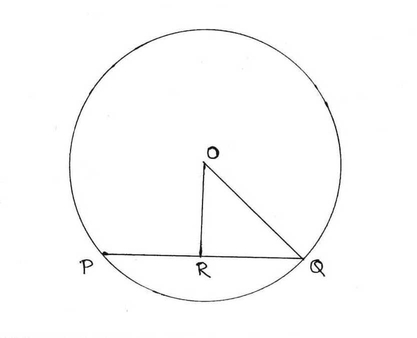
O বিন্দু থেকে PQ জ্যা-এর দূরত্ব 5 সেমি ।
∴ OR = 5 সেমি ।
এক্ষেত্রে OR , PQ এর ওপর লম্ব
বৃত্তের ব্যাসার্ধ OQ = 26/2 = 13 সেমি ।
∴ সমকোণী ত্রিভুজ ∆ ORQ এর ক্ষেত্রে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই ,
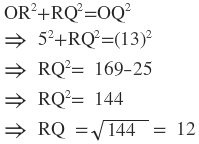
আবার, যেহেতু বৃত্তের কেন্দ্রগামী কোনও জ্যা এর ওপর অঙ্কিত লম্ব জ্যা টিকে সমদ্বিখন্ডিত করে ।তাই R , PQ এর মধ্যবিন্দু ।
∴ PQ = 12×2 =24সেমি ।
∴ PQ জ্যা-এর দৈর্ঘ্য = 24 সেমি ।
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
3. O কেন্দ্রীয় একটি বৃত্তের PQ জ্যা এর দৈর্ঘ্য 4 সেমি এবং O বিন্দু থেকে PQ এর দূরত্ব 2.1 সেমি. । বৃত্তের ব্যাসের দৈর্ঘ্য হিসাব করে রাখি ।
সমাধানঃ
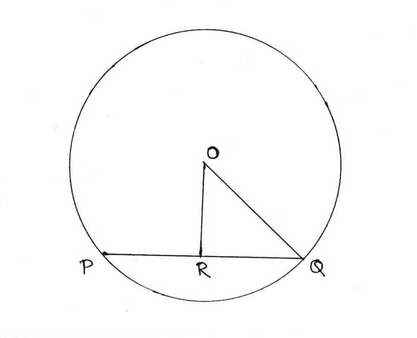
জ্যা PQ এর দৈর্ঘ্য = 4 সেমি ।
কেন্দ্র থেকে PQ জ্যা OR এর দৈর্ঘ্য = 2.1 সেমি ।
OQ যুক্ত করা হল , OQ হল বৃত্তের ব্যাসার্ধ ।
যেহেতু বৃত্তের কেন্দ্রগামী কোনও জ্যা এর ওপর অঙ্কিত লম্ব জ্যা টিকে সমদ্বিখন্ডিত করে ।তাই R , PQ এর মধ্যবিন্দু ।
∴ RQ = 4/2 সেমি = 2 সেমি ।
সমকোণী ত্রিভুজ ∆ ORQ থেকে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই ,
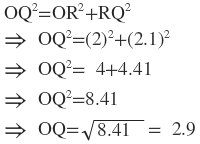
∴বৃত্তের ব্যাস = 2.9×2=5.8 সেমি ।
4. O কেন্দ্রীয় বৃত্তে 6 সেমি ও 8 সেমি দৈর্ঘ্য এর দুটি জ্যা । যদি ছোটো দৈর্ঘ্য এর জ্যা টির বৃত্তের কেন্দ্র থেকে দূরত্ব 4 সেমি হয় , তাহলে অপর জ্যা টির কেন্দ্র থেকে দূরত্ব কত তা হিসাব করে লিখি ।
সমাধানঃ
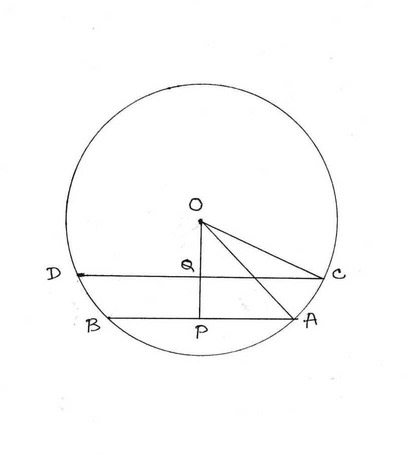
ধরি O কেন্দ্রীয় বৃত্তের AB ও CD দুটি জ্যা । AB= 6 সেমি এবং CD = 8 সেমি । কেন্দ্র O থেকে AB এর দূরত্ব = OP = 4 সেমি । ∴ OP ⊥ AB
কেন্দ্র O থেকে CD এর দূরত্ব OQ ∴ OQ ⊥ CD
O,A এবং O,C যুক্ত করা হল ।
এখন OA = OC = বৃত্তের ব্যাসার্ধ ।
যেহেতু বৃত্তের কেন্দ্রগামী কোনও জ্যা এর ওপর অঙ্কিত লম্ব জ্যা টিকে সমদ্বিখন্ডিত করে । তাই P , AB এর মধ্যবিন্দু এবং Q , CD এর মধ্যবিন্দু ।
এখন সমকোণী ত্রিভুজ ∆ OAP থেকে পাই ,
OA2=OP2+PA2
বা, OA2 = (4)2 + (6/2)2
বা, OA2 = 16+9
বা, OA = √25
বা, OA= 5
∴বৃত্তের ব্যাসার্ধ = 5 সেমি ।
আবার সমকোণী ত্রিভুজ ∆OCQ থেকে পাই ,
OQ2+QC2=OC2
বা, OQ2+(8/2)2=(5)2 [ যেহেতু OC=OA=5 সেমি ]
বা, OQ2 +16 =25
বা, OQ2 = 25-16
বা, OQ2= 9
বা, OQ = √9
বা, OQ = 3
∴ কেন্দ্র থেকে অপর জ্যাটির দূরত্ব 3 সেমি ।
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
5. যদি কোন বৃত্তের একটি জ্যা এর দৈর্ঘ্য 48 সেমি এবং কেন্দ্র থেকে ওই জ্যা এর দূরত্ব 7 সেমি হয় , তবে ওই বৃত্তের কেন্দ্র থেকে যে জ্যা এর দূরত্ব 20 সেমি , সেই জ্যা এর দৈর্ঘ্য কত হবে তা হিসাব করে লিখি ।
সমাধানঃ
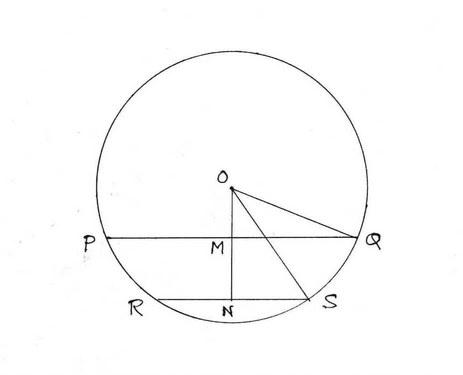
ধরি O কেন্দ্রীয় বৃত্তের PQ জ্যা এর দৈর্ঘ্য 48 সেমি এবং কেন্দ্র থেকে দূরত্ব OM=7 সেমি ।
∴ OM ⊥ PQ
ধরি, RS জ্যা এর কেন্দ্র থেকে দূরত্ব ON = 20 সেমি ।
∴ ON ⊥ RS
O,Q এবং O,S যুক্ত করা হল ।
OQ =OS = বৃত্তের ব্যাসার্ধ ।
যেহেতু বৃত্তের কেন্দ্রগামী কোনও জ্যা এর ওপর অঙ্কিত লম্ব জ্যা টিকে সমদ্বিখন্ডিত করে । তাই , M , PQ এর মধ্য বিন্দু । আবার N , RS এর মধ্যবিন্দু ।
সমকোণী ত্রিভুজ ∆OMQ থেকে পাই,
OQ2= OM2+MQ2
বা, OQ2 = (7)2+(48/2)2
বা, OQ2= 49+(24)2
বা, OQ2 = 49+576
বা, OQ2 = 625
বা, OQ = √625
বা, OQ = 25
সমকোণী ত্রিভুজ ∆ONS থেকে পাই ,
ON2+NS2 = OS2
বা, NS2 = OS2-ON2
বা, NS2 = (25)2-(20)2
বা, NS2= 625-400
বা, NS2 = 225
বা, NS = √225
বা, NS = 15
যেহেতু N , RS এর মধ্যবিন্দু
∴ RS = 2NS
বা, RS = 2×15
বা, RS = 30
∴ RS জ্যা এর দৈর্ঘ্য 30 সেমি ।
6. পাশের O কেন্দ্রীয় বৃত্তের ছবিতে OP ⊥ AB; AB = 6 সেমি এবং PC = 2 সেমি হলে, বৃত্তের ব্যাসার্ধের দৈর্ঘ্য হিসাব করে লিখি ।
সমাধানঃ
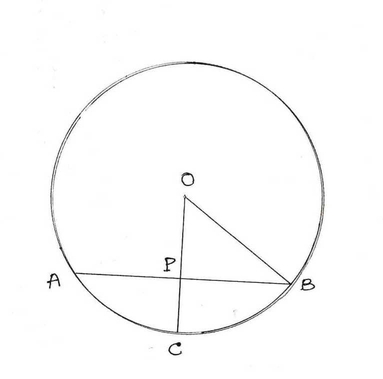
OP ⊥ AB
O,B যুক্ত করা হল
ধরি ব্যাসার্ধ x সেমি ।
∴ OB=OC=x সেমি
∴ OP = OC-PC = (x-2)সেমি
যেহেতু বৃত্তের কেন্দ্রগামী কোনও জ্যা এর ওপর অঙ্কিত লম্ব জ্যা টিকে সমদ্বিখন্ডিত করে । তাই P , AB এর মধ্যবিন্দু ।
সুতরাং PB = 6/2 =3 সেমি ।
সমকোণী ত্রিভুজ ∆OPB থেকে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই ,
OB2=OP2+PB2
বা, x2 = (x-2)2+(3)2
বা, x2 = x2-4x+4+9
বা, 4x=13
বা, x = 13/4
বা, x= 3.25
∴বৃত্তের ব্যাসার্ধ 3.25 সেমি ।
7. একটি সরলরেখা দুটি এককেন্দ্রীয় বৃত্তের একটিকে A ও B বিন্দুতে এবং অপরটিকে C ও D বিন্দুতে ছেদ করেছে । যুক্তি দিয়ে প্রমাণ করি যে AC=DB ।
সমাধানঃ
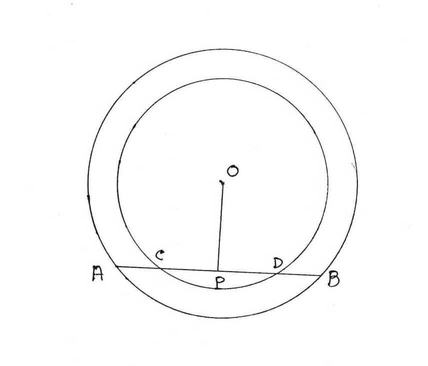
চিত্রে O কেন্দ্রীয় দুটি বৃত্তকে একটি সরলরেখা যথাক্রমে A,B এবং C,D বিন্দুতে ছেদ করেছে ।
প্রমান করতে হবে যে AB = CD
অঙ্কনঃ O থেকে AB এর ওপর একটি লম্ব OP অঙ্কন করা হল ।
প্রমানঃ যেহেতু বৃত্তের কেন্দ্রগামী কোনও জ্যা এর ওপর অঙ্কিত লম্ব জ্যা টিকে সমদ্বিখন্ডিত করে । তাই P ,AB এবং CD উভয়ের মধ্যবিন্দু ।
∴ AP=PB এবং CP=PD
সুতরাং AP-CP= PB-PD
∴ AC=DB (প্রমাণিত)
8. প্রমাণ করি , কোন বৃত্তের দুটি পরস্পরছেদী জ্যা পরস্পর কে সমদ্বিখন্ডিত করতে পারে না , যদি না উভয়েরই বৃত্তের ব্যাস হয় ।
সমাধানঃ
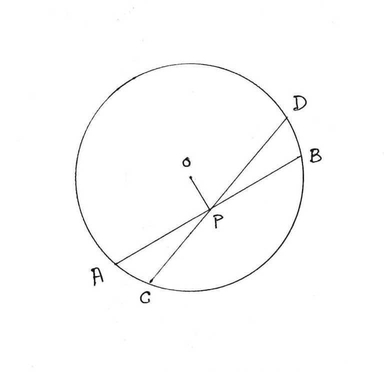
ধরি ,O কেন্দ্রীয় বৃত্তের AB ও CD দুটি পরস্পর ছেদী জ্যা এবং তারা পস্পরকে P বিন্দুতে
ছেদ করেছে । ধরা হল P , AB এর মধ্যবিন্দু ।
প্রমান করতে হবে P , CD এর মধ্যবিন্দু নয় ।
অঙ্কনঃ O , P যুক্ত করা হল ।
প্রমানঃ যেহেতু P , AB এর মধ্যবিন্দু এবং OP কেন্দ্রগামী সরলরেখা ।
∴ OP ⊥ AB
আবার AB এবং CD সরলরেখা পস্পরকে P বিন্দুতে ছেদ করেছে ,
∴ OP, একইসাথে AB এবং CD উভয় এর ওপর লম্ব হতে পারে না ।
যেহেতু বৃত্তের কেন্দ্র গামী কোনও সরলরেখাংশ কোনও জ্যা কে সমদ্বিখণ্ডিত করলে ওই সরলরেখাংশ ওই জ্যা এর ওপর লম্ব হবে ।
এক্ষেত্রে P , CD এর মধ্যবিন্দু হতে পারেনা ।
কিন্তু যদি AB ও CD পরস্পর ব্যাস হত তবে তারা পরস্পর কে সমদ্বিখণ্ডিত করত ।
9. X ও Y কেন্দ্রবিশিষ্ট দুটি বৃত্ত পরস্পর কে A ও B বিন্দুতে ছেদ করেছে । XY এর মধ্যবিন্দু S এর সঙ্গে A বিন্দু যুক্ত করলাম এবং A বিন্দু দিয়ে SA এর উপর লম্ব অঙ্কন করলাম যা বৃত্ত দুটিকে P ও Q বিন্দুতে ছেদ করলো । প্রমান করি PA = AQ ।
সমাধানঃ
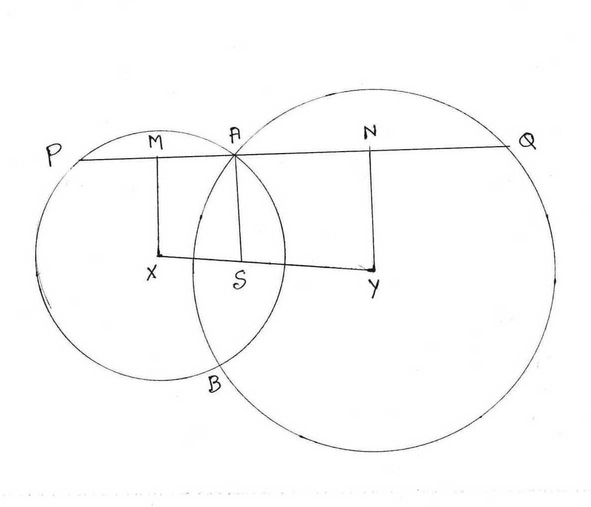
ধরি, X ও Y কেন্দ্রীয় বৃত্ত পস্পরকে A ও B বিন্দুতে ছেদ করেছে । XY এর মধ্যবিন্দু S । S এবং A যুক্ত করা হল । A বিন্দু দিয়ে S এর ওপর অঙ্কিত লম্ব বৃত্ত দুটিকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে । প্রমান করতে হবে যে , PA = AQ ।
অঙ্কনঃ X ও Y বিন্দু দিয়ে PQ এর ওপর যথাক্রমে XM এবং YN লম্ব অঙ্কন করা হল ।
প্রমানঃ অঙ্কনানুসারে XM , SA , YN তিনটি সরলরেখা প্রত্যেকে PQ এর ওপর লম্ব । সুতরাং XM ∥ SA ∥ YN
যেহেতু X ও Y যথাক্রমে বৃত্ত দুটির কেন্দ্র এবং XM , YN প্রত্যেকে PQ এর ওপর লম্ব সুতরাং M ও N যথাক্রমে PA ও AQ এর মধ্যবিন্দু ।
∴ MA = ½ PA
এবং AN = ½ AQ
আবার যেহেতু S , XY এর মধ্যবিন্দু ,
সুতরাং XS = SY
এখন XM , SA ,YN সমান্তরাল সরলরেখা তিনটি XY থেকে সমান দুটি অংশ ছিন্ন করে ,
∴ তা ওপর সরলরেখা PQ থেকেও সমান দুটি অংশ ছিন্ন করবে ।
অর্থাৎ , MA = AN
বা , ½ PA = ½ AQ [ যেহেতু MA = ½ PA এবং AN = ½ AQ ]
বা, PA = AQ ( প্রমাণিত )
10. O কেন্দ্রীয় বৃত্তের 10 সেন্টিমিটার ও 24 সেন্টিমিটার দৈর্ঘ্যের দুটি সমান্তরাল জ্যা AB ও CD কেন্দ্রের বিপরীত পার্শ্বে অবস্থিত । যদি AB ও CD জ্যা দুটির মধ্যে দূরত্ব 17 সেমি হয়, তবে হিসাব করে বৃত্তের ব্যাসার্ধের দৈর্ঘ্য লিখি ।
সমাধানঃ
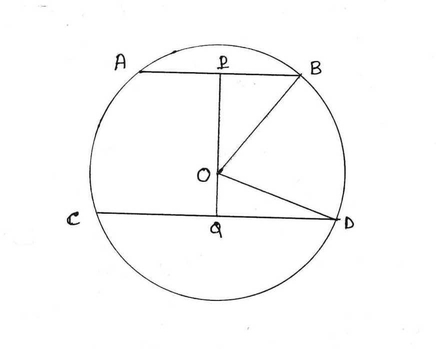
O কেন্দ্রীয় বৃত্তের দুটি জ্যা AB ও CD ।
AB = 10সেমি , CD = 24 সেমি কেন্দ্রের বিপরীত পার্শ্বে অবস্থিত ।
কেন্দ্র O থেকে AB ও CD এর ওপর যথাক্রমে OP ও OQ লম্ব ।
যেহেতু বৃত্তের কেন্দ্রগামী কোনও জ্যা এর ওপর অঙ্কিত লম্ব জ্যা টিকে সমদ্বিখন্ডিত করে
∴ P এবং Q যথাক্রমে AB ও CD এর মধ্যবিন্দু ।
সুতরাং PB= 10/2=5 সেমি
এবং QD = 24/2 = 12 সেমি
যেহেতু AB ∥ CD সেহেতু O , PQ এর ওপর অবস্থিত একটি বিন্দু ।
AB ও CD জ্যা দুটির মধ্যে দূরত্ব = PQ = 17 সেমি
O,D এবং O , B যুক্ত করা হল ।
∴ OD=OB =বৃত্তের ব্যাসার্ধ
ধরি, OP = x সেমি
∴ OQ = (17-x) সেমি ।
এখন সমকোণী ত্রিভুজ ∆ OPB থেকে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই ,
OB2=OP2+PB2
বা, OB2 = x2 + (5)2 —— (i)
আবার সমকোণী ত্রিভুজ ∆ OQD থেকে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই ,
OD2 = OQ2 +QD2
বা, OD2 = (17-x)2 + (12)2 ——-(ii)
যেহেতু, OB =OD
(i) ও (ii) থেকে পাই ,
∴ x2+ (5)2 = (17-x)2 +(12)2
বা , x2+25= (17-x)2 +144
বা, x2+25 = 289-34x+x2+144
বা, 34x = 144+289-25
বা, 34x = 408
বা, x = 408/34
বা, x = 12
(i) নং সমীকরণ থেকে পাই ,
OB2 = x2 + (5)2
বা, OB2 = (12)2+25 [ ∵ x =12 ]
বা, OB2 = 144+25
বা, OB2 = 169
বা, OB = √169
বা, OB = 13
সুতরাং বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 13 সেমি ।
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
11. দুটি বৃত্তের কেন্দ্র P এবং Q ; বৃত্ত দুটি A ও B বিন্দুতে ছেদ করে । A বিন্দু দিয়ে PQ সরলরেখাংশের সমান্তরাল সরলরেখা বৃত্ত দুটিকে C ও D বিন্দুতে ছেদ করে । প্রমান করি CD = 2PQ ।
সমাধানঃ
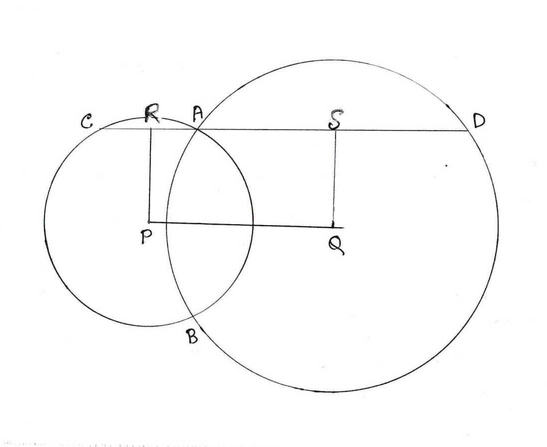
ধরি P ও Q কেন্দ্রীয় বৃত্ত দুটি পরস্পর কে A ও B বিন্দুতে ছেদ করেছে । A বিন্দু দিয়ে PQ এর সমান্তরাল সরলরেখা P ও Q কে যথাক্রমে C ও D বিন্দুতে ছেদ করেছে ।
প্রমান করতে হবে যে CD =2PQ
অঙ্কনঃ P ও Q বিন্দু দিয়ে CD এর ওপর যথাক্রমে PR ও QS লম্ব টানা হল ।
প্রমান ঃ যেহেতু PQ || RS এবং PR ⊥ CD ও QS ⊥ CD ,
∴ PRSQ একটি আয়তক্ষেত্র ।
∴ PQ = RS —— (i)
যেহেতু PR ⊥ CA এবং QS ⊥ AD
∴ R , CA এর মধ্যবিন্দু এবং S , AD এর মধ্যবিন্দু ।
অর্থাৎ , AR = ½ AC এবং AS = ½ AD
এখন, RS = AR+AS = 1/2( AC +CD) = ½ CD
∴ RS = ½ CD
⇒ 2RS = CD
⇒ 2PQ = CD [ (i) নং থেকে পাই ]
∴ CD = 2PQ [প্রমাণিত]
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
12. একটি বৃত্তের AB ও CD জ্যা দুটি সমান । প্রমান করি যে ∠ BAC এর সমদ্বিখণ্ডক কেন্দ্রগামী ।
সমাধানঃ
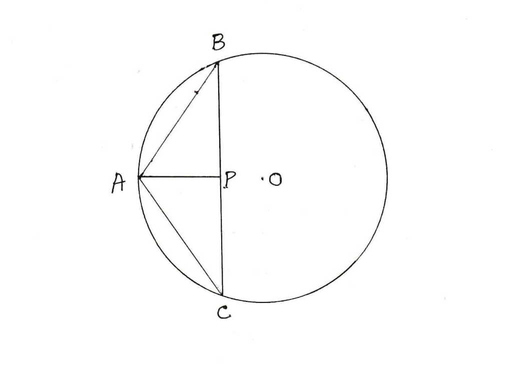
ধরি O কেন্দ্রীয় বৃত্তের AB ও CD দুটি সমান দৈর্ঘ্যের জ্যা । B ও C যুক্ত করা হল , যা ∠ BAC এর সমদ্বিখণ্ডক কে P বিন্দুতে ছেদ করে ।
প্রমানঃ ∆ABP এবং ∆ ACP এর মধ্যে,
AB =AC ( প্রদত্ত )
∠BAP = ∠ CAP [ যেহেতু AP , ∠ BAC এর সমদ্বিখণ্ডক ]
এবং AP সাধারণ বাহু
∴ বাহু- কোন – বাহু শর্তানুসারে , ∆ ABP ≅ ∆ ACP
∴ BP =CP [অনুরুপ বাহু ]
এবং ∠BPA = ∠CPA
আবার ∠ BPC = 180º
∴ ∠ BPA =∠ CPA =90º
সুতরাং AP ⊥ BC
আবার O কেন্দ্রীয় বৃত্তের BC জ্যা এবং P , BC এর মধ্যবিন্দু এবং AP⊥ BC
∴ AP কেন্দ্রগামী ( প্রমাণিত )
13. একটি বৃত্তের পরস্পর ছেদী জ্যা – এর অন্তর্ভুক্ত কোনের সমদ্বিখণ্ডক যদি কেন্দ্রগামী হয় , তাহলে প্রমান করি যে জ্যা দুটি সমান ।
সমাধানঃ
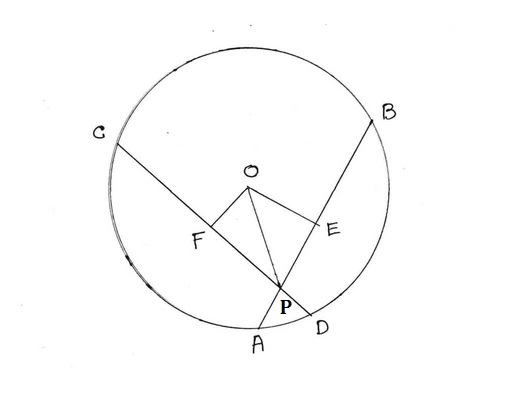
O কেন্দ্রীয় বৃত্তে AB ও CD দুটি জ্যা পরস্পর কে P বিন্দুতে ছেদ করেছে । OP , কোন APC এর সমদ্বিখণ্ডক হলে প্রমান করতে হবে যে , AB=CD
অঙ্কনঃ OE ⊥ AB এবং OF ⊥ CD অঙ্কন করা হল ।
প্রমানঃ ∆POE এবং ∆ POF এর মধ্যে
∠ OEP= ∠ OFP ( প্রত্যেকে সমকোণ )
∠ EPO = ∠ FPO ( ∵ OP, ∠ BPC এর সমদ্বিখণ্ডক )
OP সাধারণ বাহু
∴ ∆ POE ≅ ∆ POF
∴ OE=OF
অর্থাৎ জ্যা দুটি কেন্দ্র থেকে সমদূরবর্তী সুতরাং জ্যা দ্বয়ের দৈর্ঘ্য সমান ।
∴ AB =CD ( প্রমাণিত )
Koshe Dekhi 3.1 & 3.2 Class 10| বৃত্ত সম্পর্কিত উপপাদ্য কষে দেখি ৩.১।বৃত্ত সম্পর্কিত উপপাদ্য কষে দেখি ৩.২।Koshe Dekhi 3.1 Class 10| Koshe Dekhi 3.2 Class 10|WBBSE Class 10(Ten)(X) Math Solution Of Chapter 3| Ganit Prakash Class 10 Chapter 3 Solution|WB Board Class 10 Math Solution In Bengali.
14. প্রমান করি যে একটি বৃত্তে দুটি জ্যা-এর মধ্যে যে জ্যাটি কেন্দ্রের নিকটবর্তী সেটির দৈর্ঘ্য অপর জ্যা- টির দৈর্ঘ্য ওপেক্ষা বৃহত্তর ।
সমাধানঃ
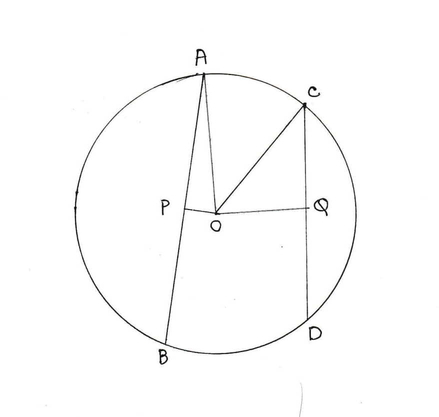
মনে করি , বৃত্তের কেন্দ্র O এবং AB ও CD ওই বৃত্তের দুটি জ্যা । OP এবং OQ যথাক্রমে AB ও CD এর ওপর লম্ব । এক্ষেত্রে OP<OQ , সুতরাং AB ও CD জ্যা দুটির মধ্যে AB জ্যা কেন্দ্র থেকে অধিকতর নিকটবর্তী ।
প্রমান করতে হবে , AB > CD
অঙ্কনঃ OA এবং OC যুক্ত করা হল ।
প্রমানঃ এখানে OP ⊥ AB এবং OQ ⊥ CD
যেহেতু বৃত্তের কেন্দ্রগামী কোনও জ্যা এর ওপর অঙ্কিত লম্ব জ্যাটিকে সমদ্বিখন্ডিত করে ,
∴ AP = AB/2
এবং CQ = CD /2
আবার , ∆AOP এবং ∆COQ উভয়ই সমকোণী ।
পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই ,
∴ OA2= AP2+PO2 এবং OC2 = OQ2+CQ2
যেহেতু OA = OC
সুতরাং ,
AP2+PO2 = OQ2+CQ2 ——- (i)
এখন OP < OQ
∴ OP2 < OQ2
তাই (i) থেকে বলা যায় , AP2 > CQ2
∴ AP > CQ
∴ (AB/2) >(CB/2)
∴ AB > CD
অর্থাৎ AB জ্যা এর দৈর্ঘ্য CD জ্যা এর দৈর্ঘ্য অপেক্ষা বৃহত্তর (প্রমাণিত) ।
15. একটি বৃত্তের ভিতর যেকোনো বিন্দু দিয়ে ক্ষুদ্রতম জ্যা কোনটি হবে তা প্রমাণ করে লিখি ।
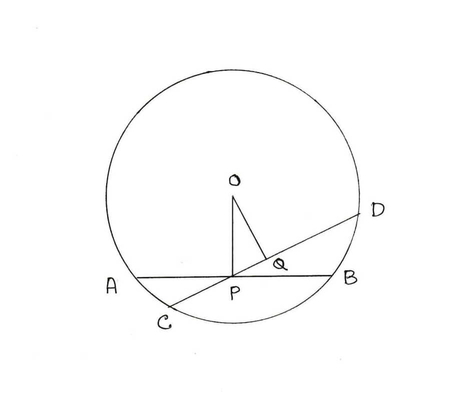
সমাধানঃ
ধরি , O কেন্দ্রীয় বৃত্তের মধ্যস্থ P যেকোনো একটি বিন্দু ।
P বিন্দু দিয়ে AB একটি জ্যা , যখন P , AB এর মধ্যবিন্দু এবং P বিন্দু দিয়ে অপর একটি জ্যা CD
অঙ্কনঃ CD এর ওপর OQ লম্ব অঙ্কন করা হলো ।
প্রমানঃ সমকোণী ত্রিভুজ ∆ OPQ এর এর OP অতিভুজ ।
∴ OP > OQ
যেহেতু বৃত্তের কেন্দ্র থেকে দূরবর্তী জ্যা ক্ষুদ্রতম হয় ,
∴ AB < CD
∴ কোনও বিন্দু দিয়ে অঙ্কিত যে জ্যাটি ক্ষুদ্রতম হবে , যখন ঐ বিন্দু জ্যাটির মধ্যবিন্দু হবে (প্রমাণিত )
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
| Madhyamik Math koshe dekhi 3.1 And 3.2. বৃত্ত সম্পর্কিত উপপাদ্য কষে দেখি ৩.১।বৃত্ত সম্পর্কিত উপপাদ্য কষে দেখি ৩.২।Koshe Dekhi 3.1 Class 10. Koshe Dekhi 3.2 Class 10.WBBSE Class 10 Math Solution Of Chapter 3. Ganit Prakash Class 10 Chapter 3 Solution.WB Board Class 10 Math Solution In Bengali. |
16. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন ( V.S.A )
(A) বহুবিকল্পীয় প্রশ্ন ( M.C.Q ) :
(i) O কেন্দ্রীয় বৃত্তের AB ও CD জ্যা দুটির দৈর্ঘ্য সমান । ∠AOB = 60 হলে, ∠COD এর মান
(a) 40 (b) 30 (c) 60 (d) 90
উত্তরঃ ( c ) 60
যেহেতু সমান সমান জ্যা কেন্দ্রে সমান কোন উৎপন্ন করে ।
(ii) একটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 13 সেমি এবং বৃত্তের একটি জ্যা- এর দৈর্ঘ্য 10 সেমি । বৃত্তের কেন্দ্র থেকে জ্যা- এর দূরত্ব
(a) 12.5 সেমি (b) 12 সেমি (c) √69 সেমি (d) 24 সেমি
উত্তরঃ ( b ) 12 সেমি.
সমাধানঃ
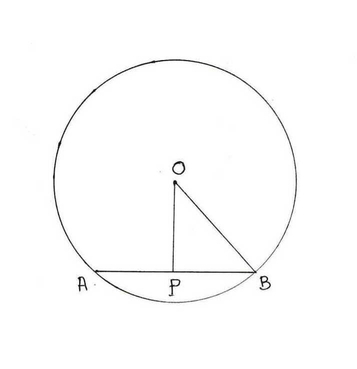
OP ⊥ AB
∴ P , AB এর মধ্যবিন্দু ।
সমকোণী ত্রভুজ OBC থেকে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই ,
OB2 = OP2+PB2
বা, 132 = OP2+(10/2)2
বা, OP2 = 169-25
বা, OP2 = 144
বা , OP = √144
বা, OP = 12
(iii) O কেন্দ্রীয় বৃত্তের AB ও CD দুটি সমান দৈর্ঘ্যের জ্যা । O বিন্দু থেকে AB জ্যা এর দূরত্ব 4 সেমি হলে, CD জ্যা – এর দূরত্ব
(a) 2 সেমি (b) 4 সেমি (c) 6 সেমি (d) 8 সেমি
উত্তরঃ (b ) 4 সেমি.
সমান দৈর্ঘ্যের জ্যা কেন্দ্র থেকে সমদূরবর্তী ।
∴ কেন্দ্র থেকে CD জ্যা- এর দূরত্ব হবে 4 সেমি.
Koshe Dekhi 3.1 & 3.2 Class 10| বৃত্ত সম্পর্কিত উপপাদ্য কষে দেখি ৩.১।বৃত্ত সম্পর্কিত উপপাদ্য কষে দেখি ৩.২।Koshe Dekhi 3.1 Class 10| Koshe Dekhi 3.2 Class 10|WBBSE Class 10(Ten)(X) Math Solution Of Chapter 3| Ganit Prakash Class 10 Chapter 3 Solution|WB Board Class 10 Math Solution In Bengali.
(iv) AB ও CD দুটি সমান্তরাল জ্যা –এর প্রত্যেকটির দৈর্ঘ্য 16 সেমি । বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 10 সেমি হলে , জ্যা দুটির মধ্যে দূরত্ব
(a) 12 সেমি (b) 16 সেমি (c) 20 সেমি (d) 5 সেমি ।
উত্তরঃ। (a) 12 সেমি.
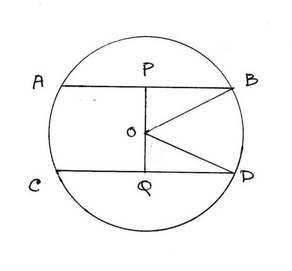
সমাধানঃ
AB =CD = 16 সেমি
∴ PB = 16/2 = 8 সেমি.
যেহেতু বৃত্তের কেন্দ্রগামী কোনও সরলরেখা ঐ বৃত্তের কোনও জ্যা-এর লম্ব হলে , সরলরেখাটি জ্যাটিকে সমদ্বিখণ্ডিত করবে ।
ব্যাসার্ধ = OB=OD =10 সেমি.
সমকোণী ত্রিভুজ POB থেকে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই ,
OB2 = OP2+PB2
বা, (10)2 = OP2 + (16/2)2
বা, (10)2 = OP2 +(8)2
বা, 100= OP2 +64
বা, OP2 = 100-64
বা, OP2 = 36
বা, OP = 6
∴ OQ = 6 সেমি. [যেহেতু,সমান দৈর্ঘ্য বিশিষ্ট জ্যা কেন্দ্র থেকে সমদূরবর্তী হয় ]
∴ PQ =OP+OQ=12 সেমি.
(v) দুটি সমকেন্দ্রীয় বৃত্তের কেন্দ্র O ; একটি সরলরেখা একটি বৃত্তকে A ও B বিন্দুতে এবং অপর বৃত্তকে C ও D বিন্দুতে ছেদ করে । AC = 5 সেমি হলে BD এর দৈর্ঘ্য
(a) 2.5 সেমি (b) 5 সেমি (c) 10 সেমি (d)কোনোটিই নয় ।
উত্তরঃ (b ) 5 সেমি.
সমাধানঃ
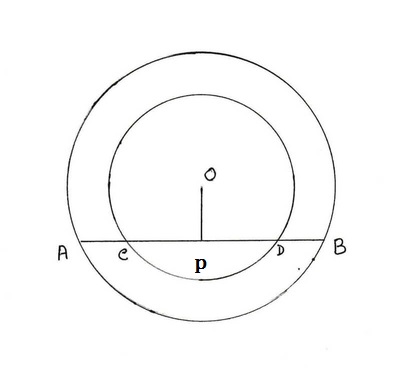
যেহেতু OP ⊥ AB
∴ PC =PD
এবং PA = PB
যেহেতু বৃত্তের কেন্দ্রগামী কোনও সরলরেখা ঐ বৃত্তের কোনও জ্যা-এর লম্ব হলে , সরলরেখাটি জ্যাটিকে সমদ্বিখণ্ডিত করবে ।
∴ PA-PC = PB-PD
বা, AC = BD
∴ AC =BD = 5 সেমি.
(B) সত্য / মিথ্যা লিখি:
(i) তিনটি সমরেখ বিন্দু দিয়ে যায় এরকম একটি বৃত্ত অঙ্কন করা যায় ।
উত্তরঃ মিথ্যা
তিনটি সমরেখ বিন্দু দিয়ে কোনও বৃত্ত অঙ্কন করা যায় না ।
(ii) ABCDA ও ABCEA বৃত্ত দুটি একই বৃত্ত ।
উত্তরঃ সত্য
যেহেতু দুটি বৃত্তের তিনটি বিন্দু সমান সুতরাং বৃত্ত দুটি একই ।
(iii) O কেন্দ্রীয় বৃত্তের AB এবং AC জ্যা দুটির OA ব্যাসার্ধের বিপরীত পার্শ্বে অবস্থিত হলে, ∠ OAB = ∠ OAC
উত্তরঃ মিথ্যা
যদি AB =AC হয় তবে বিবৃতি টি সত্য হবে ।
(C ) শূন্যস্থান পূরণ করি :
(i) O কেন্দ্রীয় বৃত্তে PQ ও RS জ্যা দুটির দৈর্ঘ্যের অনুপাত 1:1 হলে, ∠ POQ = ∠ ROS = __________________
উত্তরঃ 1:1
(ii) বৃত্তের কোন জ্যা –এর লম্বসমদ্বিখন্ডক ওই বৃত্তের ___________ ।
উত্তরঃ কেন্দ্রগামী
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
17. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A) :
(i) 10 সেমি দৈর্ঘ্যের ব্যাসার্ধের দুটি সমান বৃত্ত পরস্পরকে ছেদ করে এবং তাদের সাধারন জ্যা -এর দৈর্ঘ্য 12 সেমি । বৃত্ত দুটির কেন্দ্রদ্বয়ের মধ্যে দূরত্ব নির্ণয় করি ।
সমাধানঃ
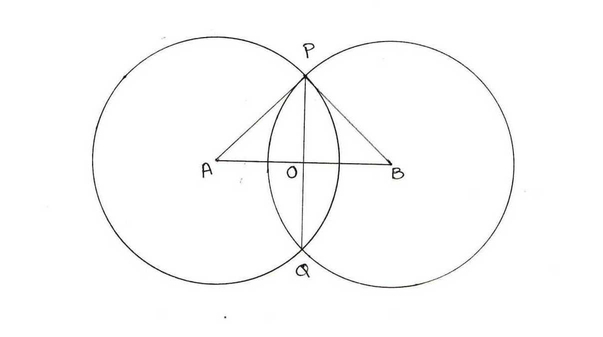
A ও B কেন্দ্রীয় বৃত্তের PQ সাধারণ জ্যা ।
A ও B যুক্ত করলে , AB ⊥ PQ হয় ।
সমকোণী △AOP এর ,
AP2= OP2+AO2
বা, (10)2 = (12/2)2+(AO)2
বা, 100 = (6)2 +AO2
বা, 100 = 36 + AO2
বা, AO2= 100-36
বা, AO2 = 64
বা, AO2 = (8)2
বা, AO = 8
যেহেতু বৃত্ত দুটির ব্যাসার্ধ সমান সেহেতু OA =OB = 8 সেমি. ।
∴ AB = 8+8 = 16 সেমি.
∴ বৃত্ত দুটির কেন্দ্রদ্বয়ের মধ্যে দূরত্ব = 16 সেমি. । ( উত্তর )
(ii) 5 সেমি দৈর্ঘ্যের ব্যাসার্ধের একটি বৃত্তে AB এবং AC দুটি সমান দৈর্ঘ্যের জ্যা । বৃত্তের কেন্দ্র ABC ত্রিভুজের বাইরে অবস্থিত । AB=AC = 6 সেমি হলে , BC জ্যা-এর দৈর্ঘ্য নির্ণয় করি ।
সমাধানঃ
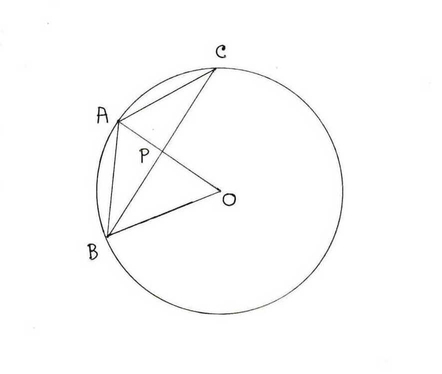
O কেন্দ্রীয় বৃত্তে , AB = AC =6 সেমি.
যেহেতু সমান দৈর্ঘ্য বিশিষ্ট জ্যা-এর মধ্যবর্তী কোনের সমদ্বিখণ্ডক কেন্দ্রগামী হয় ,
∴ OA = বৃত্তের ব্যাসার্ধ = 5 সেমি
এবং P , BC এর মধ্যবিন্দু ও OP ⊥ BC
O ,B যোগ করা হল ।
ধরি , OP = x সেমি
সমকোণী ∆ APB থেকে পাই ,
AP2 +BP2=AB2
বা, BP2 = AB2-AP2
বা , BP2 = (6)2 – AP2 ——-(i)
সমকোণী ∆OPB থেকে পাই ,
OP2+BP2 = OB2
বা, BP2= OB2-OP2
বা, BP2 = (5)2 – OP2 —— (ii)
(i) নং ও (ii) নং সমীকরণ থেকে পাই ,
(6)2– AP2 = (5)2– OP2
বা, 36 – AP2 = 25- OP2
বা, 36-25 = AP2 – OP2
বা, AP2 – OP2 = 11
বা, (OA-OP)2 – OP2 = 11
বা, (5-OP)2 – OP2 =11
বা, 25 -10OP +OP2-OP2=11
বা, 10OP = 14
বা , OP = 14/10
বা, OP = 7/5
(ii) নং সমীকরণ থেকে পাই ,
BP2 = 25- (7/5)2
বা, BP2 = 25- (49/25)
বা, BP2 = (625-49)/25
বা , BP2 = 576/25
বা, BP = 24/5 [ উভয় পক্ষে বর্গমূল করে পাই ]
∴ CD = 2BP = 2×(24/5) = 48/5 = 9.6 সেমি. ।( উত্তর )
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
| Koshe Dekhi 3.1 & 3.2 Class 10| বৃত্ত সম্পর্কিত উপপাদ্য কষে দেখি ৩.১।বৃত্ত সম্পর্কিত উপপাদ্য কষে দেখি ৩.২।Koshe Dekhi 3.1 Class 10| Koshe Dekhi 3.2 Class 10|WBBSE Class 10(Ten)(X) Math Solution Of Chapter 3| Ganit Prakash Class 10 Chapter 3 Solution|WB Board Class 10 Math Solution In Bengali. |
(iii) O কেন্দ্রীয় বৃত্তে AB ও CD জ্যা দুটির দৈর্ঘ্য সমান । ∠ AOB = 60º এবং CD=6 সেমি হলে, বৃত্তের ব্যাসার্ধের দৈর্ঘ্য কত তা নির্ণয় করি ।
সমাধানঃ
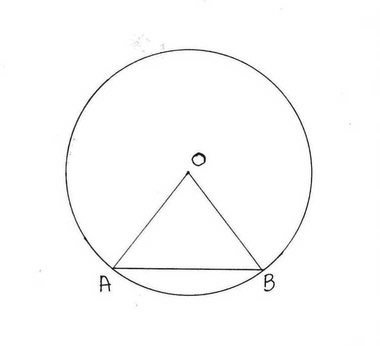
OAB এর OA =OB = বৃত্তের ব্যাসার্ধ
∴ ∠OAB = ∠ OBA
এবং ∠ AOB = 60º ( প্রদত্ত )
∠OAB=∠OBA=60º
অর্থাৎ OAB সমবাহু ত্রিভুজ ।
যার , OA =OB =AB= 6 সেমি.
∴ বৃত্তের ব্যাসার্ধ = 6 সেমি.( উত্তর )
| Koshe Dekhi 3.1 & 3.2 Class 10| বৃত্ত সম্পর্কিত উপপাদ্য কষে দেখি ৩.১।বৃত্ত সম্পর্কিত উপপাদ্য কষে দেখি ৩.২।Koshe Dekhi 3.1 Class 10| Koshe Dekhi 3.2 Class 10|WBBSE Class 10(Ten)(X) Math Solution Of Chapter 3| Ganit Prakash Class 10 Chapter 3 Solution|WB Board Class 10 Math Solution In Bengali. |
(iv) O কেন্দ্রীয় বৃত্তের ভিতর P যে কোন একটি বিন্দু । বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি এবং OP =3 সেমি হলে, P বিন্দুগামী যে জ্যা -টির দৈর্ঘ্য ন্যূনতম তা নির্ণয় করি ।
সমাধানঃ
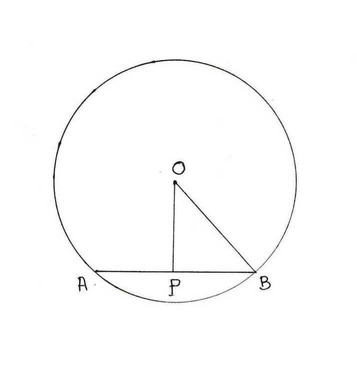
ধরি P বিন্দুগামী AB কুদ্রতম জ্যা ।
∴ P ,AB এর মধ্যবিন্দু ।
অর্থাৎ , OP ⊥ AB
সমকোণী ∆OPB থেকে পাই ,
BP2 = OB2 –OP2
বা, BP2 = (5)2-(3)2
বা, BP2 = 25-9
বা, BP2 = 16
বা, BP = 4
∴ AB জ্যাটির দৈর্ঘ্য = 2×BP = 2×4 =8 সেমি. ( উত্তর )
Koshe Dekhi 3.1 & 3.2 Class 10| বৃত্ত সম্পর্কিত উপপাদ্য কষে দেখি ৩.১।বৃত্ত সম্পর্কিত উপপাদ্য কষে দেখি ৩.২।Koshe Dekhi 3.1 Class 10| Koshe Dekhi 3.2 Class 10|WBBSE Class 10(Ten)(X) Math Solution Of Chapter 3| Ganit Prakash Class 10 Chapter 3 Solution|WB Board Class 10 Math Solution In Bengali.
(v) P ও Q কেন্দ্র বিশিষ্ট দুটি বৃত্ত A ও B বিন্দুতে ছেদ করে । A বিন্দু দিয়ে PQ এর সমান্তরাল সরলরেখা বৃত্ত দুটি কে যথাক্রমে C ও D বিন্দুতে ছেদ করে । PQ = 5 সেমি হলে , CD এর দৈর্ঘ্য কত তার নির্ণয় করি ।
সমাধানঃ
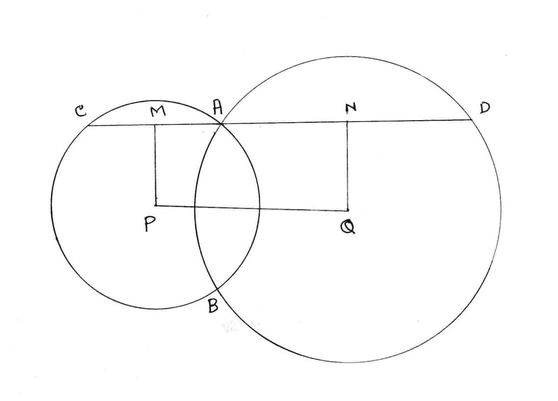
P ও Q বিন্দুতে PM ও QN লম্ব হলে ,
AM = ½ CA এবং AN = ½ AD
∴ MN = ½ CD
আবার যেহেতু PQ ∥ CD এবং PM ∥ QN
∴ PQ = MN
∴ PQ = ½ CD
বা , CD = 2PQ = 2×5=10 সেমি.( উত্তর )
Koshe Dekhi 3.1 & 3.2 Class 10| বৃত্ত সম্পর্কিত উপপাদ্য কষে দেখি ৩.১।বৃত্ত সম্পর্কিত উপপাদ্য কষে দেখি ৩.২।Koshe Dekhi 3.1 Class 10| Koshe Dekhi 3.2 Class 10|WBBSE Class 10(Ten)(X) Math Solution Of Chapter 3| Ganit Prakash Class 10 Chapter 3 Solution|WB Board Class 10 Math Solution In Bengali.
আরও পড়ুনঃ
- নবম শ্রেণি সকল বিষয়ের মক টেস্ট
- দশম শ্রেণি সকল বিষয়ের মক টেস্ট
- মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধান
- গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধান
- গণিতপ্রভা অষ্টম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধান
- সৌরেন্দ্রনাথ দে দ্বাদশ শ্রেণি সকল অধ্যায়ের সমাধান
- মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধান
- WBBSE Official Site
Amazing ,,
Thank you for help 😊
Good effort
Thanks☺️
Thanks ☺️☺️
Thanks 😁
Thank you so much
Thank you so much sar , Mam Thank you For halp
Many many thanks
You don’t know how you have helped me!!! Thank you soooo much!!!!
Thank you very much
I like maths 💯💯
Thanks