Koshe dekhi 7.3 Class 10|বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য কষে দেখি ৭.৩

Koshe dekhi 7.3 Class 10|Koshe dekhi 7.3 Class10|বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য কষে দেখি ৭.৩|মাধ্যামিক গণিত প্রকাশ সমাধান|WBBSE Madhyamik Class 10(Ten)(X) Math Solution Of Chapter 7| Ganit Prakash Class 10 Solution Of Chapter 7|কষে দেখি ৭.৩ ক্লাস ১০(টেন) সমাধান

মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন

মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন

Koshe dekhi 7.3 Class 10|বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য কষে দেখি ৭.৩|কষে দেখি 7.3 ক্লাস 10

1.ABC ত্রিভুজের B কোনটি সমকোণ । যদি AC – কে ব্যাস করে একটি বৃত্ত অঙ্কন করি যা AB কে D বিন্দুতে ছেদ করে , তবে নীচের তথ্য গুলির মধ্যে কোনটি সঠিক লিখি –

(i) AB>AD

(ii) AB=AD

(iii) AB<AD

সমাধানঃ আমরা জানি , অর্ধবৃত্তস্থ কোণ সমকোণ এবং এক্ষেত্রে AC বাহুর ওপর বিপরীত কৌনিক বিন্দু B এবং B সমকোণ

বৃত্তটি AB কে D বিন্দুতে ছেদ করলে D সমকোণ হবে । একই সরলরেখার ওপর পৃথক দুটি বিন্দু থেকে কোণ সমান হতে পারে না ।

∴ B ও D একই বিন্দুতে অবস্থিত ।

অর্থাৎ , AB =AD

(ii) AB=AD (সত্য )

Koshe dekhi 7.3 Class 10|বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য কষে দেখি ৭.৩|কষে দেখি 7.3 ক্লাস 10

2. প্রমান করি একটি সমদ্বিবাহু ত্রিভুজের সমান বাহু দুটির যে- কোনোটিকে ব্যাস করে অঙ্কিত বৃত্ত অসমান বাহুটিকে সমদ্বিখন্ডিত করে ।

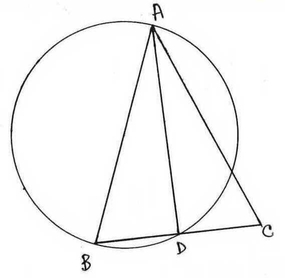
ধরি , ∆ABC একটি সমদ্বিবাহু ত্রিভুজ যার AB =AC , AB বাহুকে ব্যাস করে একটি বৃত্ত অঙ্কন করলে বৃত্তটি BC কে D বিন্দুতে ছেদ করেছে ।

প্রমান করতে হবে যে , বৃত্তটি ∆ABC ত্রিভুজের অসমান বাহু অর্থাৎ BC কে সমদ্বিখন্ডিত করে ।

অঙ্কনঃ AD যুক্ত করা হল ।

প্রমানঃ AB বৃত্তের ব্যাস

∴ ∠ADB অর্ধবৃত্তস্থ কোণ

∴ ∠ADB = 90°

∴ AD ⊥ BC

এখন , ∆ABD ও ∆ACD এর মধ্যে ,

AB =AC [ প্রদত্ত ]

∠ADB=∠ADC [ উভয়ই 90°]

AD সাধারণ বাহু

∴ ∆ABD ≅ ∆ACD

∴ BD=DC

∴ D, BC এর মধ্যবিন্দু

∴ বৃত্তটি সমদ্বিবাহু ত্রিভুজটির অসমান বাহুটিকে সমদ্বিখন্ডিত করে ।

Koshe dekhi 7.3 Class 10|বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য কষে দেখি ৭.৩|কষে দেখি 7.3 ক্লাস 10

3. সাহানা দুটি বৃত্ত এঁকেছে যারা পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে । PA ও PB যথাক্রমে দুটি বৃত্তের ব্যাস হলে , প্রমান করি  যে A ,Q ও B বিন্দুত্রয় সমরেখ ।

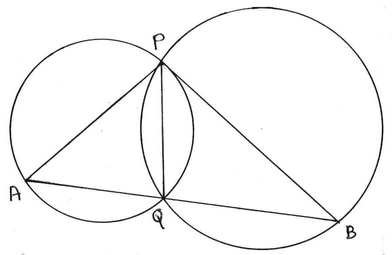
দুটি বৃত্ত পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে , PA ও PB যথাক্রমে দুটি বৃত্তের ব্যাস প্রমান করেতে হবে যে A , Q ও B বিন্দুত্রয় সমরেখ ।

অঙ্কনঃ P ,Q যুক্ত করা হল ।

প্রমানঃ ∆APQ ত্রিভুজে , AP ব্যাস ।

∴ ∠AQP = 90° [ যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ ]

আবার , ∆BQP ত্রিভুজে , PB ব্যাস

∴ ∠PQB = 90° [ যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ ]

এখন , ∠AQB

=∠AQP+∠PQB

=90°+90°

=180°

∴ A ,Q ও B একই সরলরেখায় অবস্থিত ।

∴ A ,Q ও B সমরেখ (প্রমাণিত) ।

Koshe dekhi 7.3 Class 10|বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য কষে দেখি ৭.৩|কষে দেখি 7.3 ক্লাস 10

মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে

4. রজত একটি সরলরেখাংশ PQ এঁকেছে যার মধ্যবিন্দু R এবং সে PR ও PQ –কে ব্যাস করে দুটি বৃত্ত অঙ্কন করেছে । আমি P বিন্দুগামী একটি সরলরেখা অঙ্কন করেছি যা প্রথম বৃত্ত কে S বিন্দুতে এবং দ্বিতীয় বৃত্তকে T বিন্দুতে ছেদ করেছে । যুক্তি দিয়ে প্রমান করি যে PS = ST

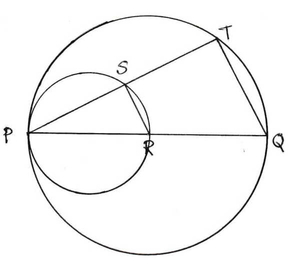
সমাধানঃ PQ একটি সরলরেখা অঙ্কন করা হল যার মধ্যবিন্দু R । PR ও PQ কে ব্যাস করে দুটি বৃত্ত অঙ্কন করা হয়েছে । P বিন্দুগামী একটি সরলরেখা অঙ্কন করা হয়েছে যা প্রথম বৃত্তকে S বিন্দুতে এবং দ্বিতীয় বৃত্তকে T বিন্দুতে ছেদ করেছে । প্রমান করতে হবে যে , PS = ST

অঙ্কনঃ  S ,R এবং T , Q যোগ করা হল ।

প্রমানঃ PR ব্যাস

∴ ∠PSR =90° [যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ ]

আবার , PQ ব্যাস

∴ ∠PTQ = 90° [ যেহেতু অর্ধবৃত্তস্থ কোণ সমকোণ ]

এখন , ∆PSR এবং ∆PTQ ত্রিভুজে ,

∠PSR = ∠PTQ [ উভয়ই 90°]

∴ SR ∥ TQ

আবার , R , PQ-এর মধ্যবিন্দু

∵একটি ত্রিভুজের কোনো বাহুর মধ্যবিন্দু দিয়ে অঙ্কিত দ্বিতীয় বাহুর সমান্তরাল সরলরেখা তৃতীয় বাহুকে সমদ্বিখন্ডিত করে

∴ S , PT এর মধ্যবিন্দু

∴ PS = ST [ প্রমাণিত ]

Koshe dekhi 7.3 Class 10|বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য কষে দেখি ৭.৩|কষে দেখি 7.3 ক্লাস 10

মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন

5.একটি বৃত্তের ওপর তিনটি বিন্দু P ,Qও R অবস্থিত । PQ ও PR এর ওপর P বিন্দুতে অঙ্কিত লম্ব দুটি বৃত্তকে যথাক্রমে S ও T বিন্দুতে ছেদ করেছে ।প্রমান করি যে RQ =ST

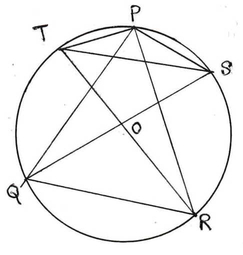
ধরাযাক , O কেন্দ্রীয় বৃত্তের ওপর P ,Q এবং R তিনটি বিন্দু । PQ ও PR এর ওপর P বিন্দুতে অঙ্কিত লম্বদুটি বৃত্তকে যথাক্রমে S ও T  বিন্দুতে ছেদ করেছে ।

প্রমান করতে হবে যে, RQ=ST

অঙ্কনঃ S ,Q ; T,R যুক্ত করা হল ।

প্রমানঃ যেহেতু, PQ ও PR এর ওপর P বিন্দুতে অঙ্কিত লম্ব দুটি বৃত্তকে যথাক্রমে S ও T বিন্দুতে ছেদ করেছে ।

∴ ∠TPR = 90° এবং ∠SPQ = 90°

যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ

∴ TR এবং SQ উভয়ই বৃত্তের ব্যাস ।

এখন , ত্রিভুজ ∆OST এবং ∆ORQ এর মধ্যে ,

OT = OS [ একই বৃত্তের ব্যাসার্ধ ]

OQ=OR [ একই বৃত্তের ব্যাসার্ধ ]

∠SOT = ∠QOR [ বিপ্রতীপ কোণ ]

∴ ∆SOT ≅ ∆PQR

∴ ST=QR [প্রমাণিত]

Koshe dekhi 7.3 Class 10|বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য কষে দেখি ৭.৩|কষে দেখি 7.3 ক্লাস 10

মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন

গণিত প্রকাশ সমাধান ক্লাস ৯

6.∆ABC একটি সূক্ষ্মকোণী ত্রিভুজ। ∆ABC ত্রিভুজের পরিবৃত্তের ব্যাস AP ; BE ও CF যথাক্রমে AC ও AB বাহুর ওপর লম্ব এবং তারা পরস্পরকে Q বিন্দুতে ছেদ করে । প্রমান করি যে BPCQ একটি সামান্তরিক ।

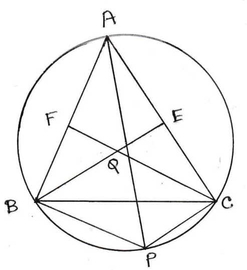
∆ABC একটি সূক্ষ্মকোণী ত্রিভুজ । ∆ABC এর পরিবৃত্তের ব্যাস AP ; BE ও CF যথাক্রমে AC ও AB বাহুর ওপর লম্ব এবং তারা পরস্পরকে  Q বিন্দুতে ছেদ করে । প্রমান করতে হবে BPCQ একটি সামান্তরিক ।

অঙ্কনঃ B,P এবং  C,P যুক্ত করা হল ।

প্রমানঃ যেহেতু , AP বৃত্তের ব্যাস

∴ ∠ABP =90°

আবার, ∠CFB = 90° [যেহেতু,CF,AB এর ওপর লম্ব]

∴ FC ∥ BP

অর্থাৎ , QC ∥ BP—-(i)

আবার , যেহেতু AP বৃত্তের ব্যাস

∴ ∠ACP = 90°

আবার , ∠BEC = 90° [ যেহেতু , BE , AC এর ওপর লম্ব ]

∴ BE ∥ PC

অর্থাৎ BQ ∥ PC—-(ii)

∴(i) ও (ii) থেকে পাই ,

∴ BPCQ একটি সামান্তরিক [প্রমাণিত] ।

Koshe dekhi 7.3 Class 10|বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য কষে দেখি ৭.৩|কষে দেখি 7.3 ক্লাস 10

7. একটি ত্রিভুজের শীর্ষকোণের অন্তঃ সমদ্বিখণ্ডক ও বহির্সমদ্বিখন্ডক ত্রিভুজটির পরিবৃত্তকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে । প্রমান করি যে PQ বৃত্তের একটি ব্যাস ।

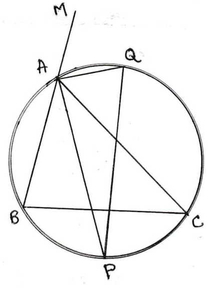
ধরি , ∆ABC এর ∠BAC এর অন্তর্দ্বিখন্ডক ও বহির্দ্বিখন্ডক ত্রিভুজটির পরিবৃত্তকে P ও Q বিন্দুতে ছেদ করে । প্রমান করতে হবে PQ বৃত্তের একটি ব্যাস ।

প্রমানঃ যেহেতু , AP ও AQ উভয়ই যথাক্রমে ∠BAC এর অন্তর্দ্বিখন্ডক এবং বহির্দ্বিখন্ডক ;

সুতরাং , ∠PAQ = 1 সমকোণ [ যেহেতু , কোনো কোণের অন্তর্দ্বিখন্ডক এবং বহির্দ্বিখন্ডক -এর মধ্যবর্তী কোণ 1 সমকোণ ]

∴ ∠PAQ অর্ধবৃত্তস্থ কোণ ।

∴ PQ বৃত্তের ব্যাস [প্রমাণিত]

8. AB ও CD একটি বৃত্তের দুটি ব্যাস । প্রমান করি যে , ACBD একটি আয়তকার চিত্র ।

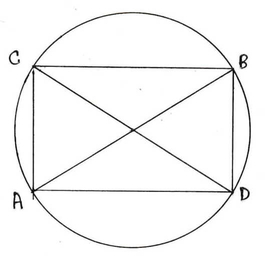
AB এবং CD বৃত্তের দুটি ব্যাস । প্রমান করতে হবে যে , ACBD একটি আয়তকার চিত্র ।

অঙ্কনঃ A,D;A,C এবং B,C যুক্ত করা হল ।

প্রমানঃ যেহেতু AB বৃত্তের ব্যাস

∴ ∠ACB =∠ADB = 1 সমকোণ [ যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ ]

আবার , যেহেতু CD বৃত্তের ব্যাস ,

∴ ∠CAD = ∠DBC = 1 সমকোণ [ যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ ]

∴ ACBD চতুর্ভুজের চারটি কোণ প্রত্যেকে সমকোণ ।

∴ ACBD একটি আয়তকার চিত্র । [প্রমাণিত]

মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে

9. প্রমান করি , একটি রম্বসের বাহুগুলিকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তগুলি একটি নির্দিষ্ট বিন্দু দিয়ে যায় ।

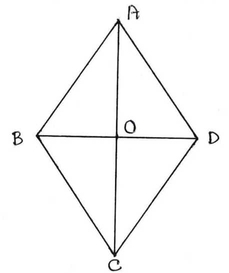
ABCD একটি রম্বস । প্রমান করতে হবে যে , রম্বসের বাহুগুলিকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তগুলি একটি নির্দিষ্ট বিন্দু দিয়ে যাবে ।

অঙ্কনঃ A ,C এবং B,D যুক্ত করা হল যারা পরস্পরকে O বিন্দুতে ছেদ করল ।

প্রমানঃ যেহেতু রম্বসের কর্ণগুলি পরস্পরকে সমকোণে সমদ্বিখন্ডিত করে , সুতরাং ,

∠AOB = ∠BOC = ∠COD = ∠DOA = 90°

আবার যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ , তাই AB বা BC বা CD বা DA যেকোনো বাহুকে ব্যাস ধরে বৃত্ত অঙ্কন করলে তা O বিন্দু দিয়ে যাবে ।

∴ রম্বসের বাহুগুলিকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তগুলি একটি নির্দিষ্ট বিন্দু দিয়ে যাবে [প্রমাণিত]

10. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A)

(A) বহু বিকল্পীয় প্রশ্ন (M.C.Q)

(i) O কেন্দ্রীয় বৃত্তে PQ একটি ব্যাস এবং PR = RQ ; ∠RPQ এর মাণ

(a) 30°

(b) 90°

(c ) 60°

(d) 45°

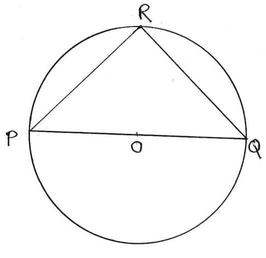
Ans: (d) 45°

সমাধানঃ

PQ ব্যাস

∴ ∠PRQ= 90°

আবার , PR =RQ

∴ ∠RPQ = ∠RQP

এখন , ∆PRQ তে ,

 ∠RPQ+∠PRQ+∠PQR = 180°

বা, ∠RPQ+90+∠RPQ = 180° [∵∠RPQ =∠RQP ]

বা, 2∠RPQ+90°=180°

বা, 2∠RPQ = 90°

বা, ∠RPQ = 45°

Koshe dekhi 7.3 Class 10|বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য কষে দেখি ৭.৩|কষে দেখি 7.3 ক্লাস 10

(ii) PQ বৃত্তের একটি জ্যা এবং POR বৃত্তের একটি ব্যাস । OD , QR বাহুর ওপর লম্ব । OD = 4 সেমি. হলে PQ- এর দৈর্ঘ্য

(a) 4 সেমি.

(b) 2 সেমি.

(c ) 8 সেমি.

(d) কোনোটিই নয়

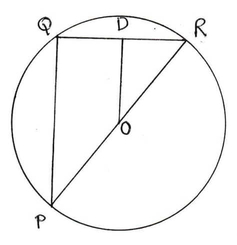
Ans: (c ) 8 সেমি.

সমাধানঃ OD ⊥ QR

আবার , O হল বৃত্তের কেন্দ্র

∴ D, QR এর মধ্যবিন্দু

∴ O, বৃত্তের কেন্দ্র এবং PR ব্যাস ।

∴ OD = ½ PQ [∵ ত্রিভুজের যেকোনো দুটি বাহুর মধ্যবিন্দুর সংযোজক সরলরেখার দৈর্ঘ্য তৃতীয় বাহুর সমান্তরাল ও অর্ধেক ]

বা, PQ = 2OD

বা, PQ = 2✕4 = 8 সেমি.

(iii) AOB বৃত্তের ব্যাস । AC এবং BD জ্যা দুটিকে বর্ধিত করলে E বিন্দুতে মিলিত হয় । ∠COD = 40° হলে ∠CED এর মাণ

(a) 40°

(b) 80°

(c ) 20°

(d) 70°

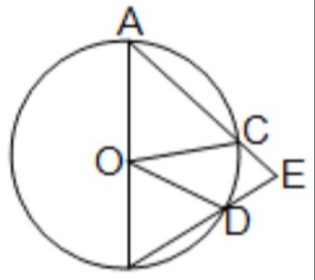
Ans: (d) 70°

সমাধানঃ

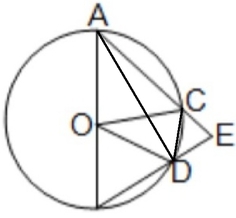
A,D এবং C ,D যুক্ত করা হল ।

∠ADB = 90° [ যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ ]

∴ ∠ADE = 90°

CD , বৃত্তচাপের ওপর CAD বৃত্তস্থ কোণ এবং COD পরিধিস্থ কোণ ।

সুতরাং , ∠CAD = ½ ✕∠COD

বা , ∠CAD = ½✕ 40°

বা, ∠CAD = 20°

∆AED তে, ∠ADE +∠DAE+∠AED = 180°

বা, 90°+20°+∠AED = 180°

বা, ∠AED = 70°

(iv) AOB বৃত্তের ব্যাস । AC = 3 সেমি. ও BC = 4 সেমি. হলে AB এর দৈর্ঘ্য

(a) 3 সেমি

(b) 4 সেমি.

(c) 5 সেমি.

(d) 8 সেমি.

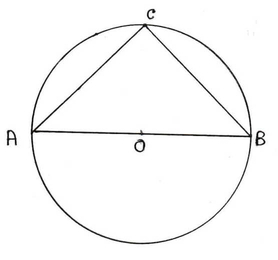
Ans: (c) 5 সেমি.

সমাধানঃ

AOB বৃত্তের ব্যাস

∴ ∠ACB = 90° [যেহেতু অর্ধবৃত্তস্থ কোণ 1 সমকোণ ]

এখন , ∆ACB ত্রিভুজে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই ,

AC²+BC²=AB²

বা, (3)² +(4)² = AB²

বা , AB² = 25

বা , AB=5[ উভয় পক্ষে বর্গমূল করে পাই ]

(v) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস । ∠BAE = 20° , ∠CAE = 25° হলে , ∠AEC এর মাণ

(a) 50°

(b) 90°

(c ) 45°

(d) 20°

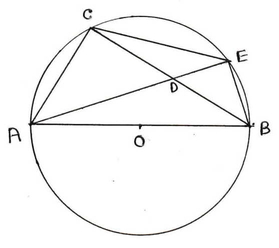
Ans: (c ) 45°

সমাধানঃ

∠BAE = ∠BCE = 20° [ একই বৃত্তাংশস্থ সকল কোণের মাণ সমান ]

∠CAE = 25° ( প্রদত্ত )

আবার , ∠ACB = 90°

∆ACE থেকে পাই ,

∠ACE+∠CAE+∠AEC = 180°

∠ACB+∠BCE+∠CAE+∠AEC = 180°

90+20+25+∠AEC=180°

135+∠AEC = 180°

∠AEC = 180°-135°

∠AEC = 45°

WBBSE

মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন

B. সত্য বা মিথ্যা লিখিঃ

(i) অর্ধবৃত্ত অপেক্ষা বৃহত্তর বৃত্যাংশস্থ কোণ স্থূলকোণ ।

উত্তরঃ মিথ্যা ।

(ii) ABC ত্রিভুজের AB বাহুর মধ্যবিন্দু O এবং OA = OB=OC ; AB বাহুকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তটি C বিন্দু দিয়ে যাবে ।

উত্তরঃ সত্য

(C ) শূন্যস্থান পূরণ করিঃ

(i) অর্ধ বৃত্তস্থ কোণ _____________ ।

উত্তরঃ সমকোণ

বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য কষে দেখি ৭.৩

(ii) অর্ধবৃত্ত অপেক্ষা ক্ষুদ্রতর বৃত্তাংশস্থ কোণ _________ ।

উত্তরঃ স্থূলকোণ

বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য কষে দেখি ৭.৩

(iii) সমকোণী ত্রিভুজের অতিভুজকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তটি ___________ বিন্দু দিয়ে যাবে ।

উত্তরঃ সমকৌণিক

Koshe dekhi 7.3 Class 10|বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য কষে দেখি ৭.৩|কষে দেখি 7.3 ক্লাস 10

মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন

11. সংক্ষিপ্ত উত্তর ধর্মী প্রশ্ন (S.A.)

(i) ∆ABC সমদ্বিবাহু ত্রিভুজের AB=AC; AB বাহুকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তটি BC বাহুকে D বিন্দুতে ছেদ করে , BD = 4 সেমি. হলে CD এর দৈর্ঘ্য নির্ণয় করো ।

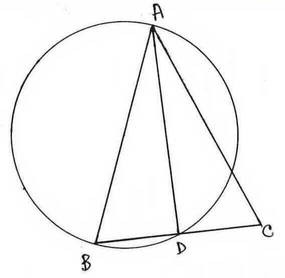
সমাধানঃ ∆ABC সমদ্বিবাহু ত্রিভুজের AB=AC

AB বাহুকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তটি BC বাহুকে D বিন্দুতে ছেদ করে ।

∴ ∠ADB = 90° [∵অর্ধবৃত্তস্থ কোণ 1 সমকোণ ]

∴ AD⊥ BC

∴ D, BC এর মধ্যবিন্দু [∵ বৃত্তের কেন্দ্রগামী কোনো সরলরেখা, ব্যাস নয় এরূপ কোনো জ্যা এর ওপর লম্ব হলে ওই সরলরেখাটি ওই জ্যা কে সমদ্বিখন্ডিত করে ]

∴ BD=CD

∴ CD = 4 সেমি.[উত্তর]

Koshe dekhi 7.3 Class 10|বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য কষে দেখি ৭.৩|কষে দেখি 7.3 ক্লাস 10

মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে

(ii) একটি বৃত্তে দুটি জ্যা AB ও AC পরস্পর লম্ব । AB = 4 সেমি. ও AC = 3 সেমি. হলে , বৃত্তের ব্যাসার্ধের দৈর্ঘ্য নির্ণয় করি ।

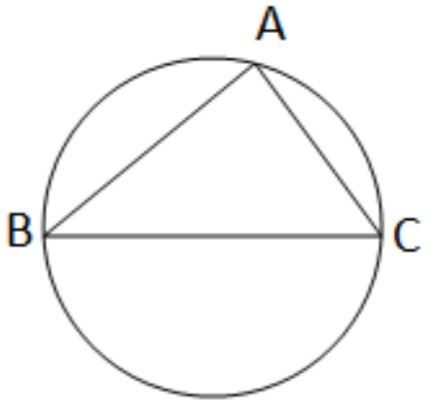
সমাধানঃ যেহেতু,  AB ও AC জ্যা দুটি পরস্পর লম্ব ।

∠BAC = 90° [ অর্ধবৃত্তস্থ কোণ ]

∴ BC বৃত্তের ব্যাস

এখন , ∆ABC সমকোণী ত্রিভুজ থেকে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই ,

BC²=AB²+AC²

বা, BC²= (4)² + (3)²

বা, BC² = 16+9

বা, BC²= 25

বা, BC = 5

∴ বৃত্তের ব্যাসার্ধ = BC /2 = 5/2 = 2.5 সেমি.[উত্তর]

Madhyamik Math Koshe dekhi 7.3 |বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য কষে দেখি ৭.৩

(iii) একটি বৃত্তে দুটি জ্যা PQ ও PR পরস্পর লম্ব । বৃত্তের ব্যাসার্ধের দৈর্ঘ্য r সেমি. হলে জ্যা QR এর দৈর্ঘ্য নির্ণয় করি ।

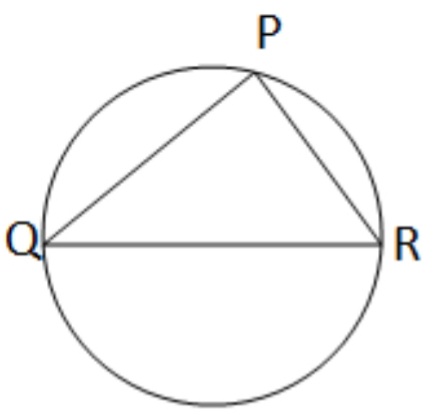
সমাধানঃ যেহেতু,  PQ ও PR জ্যা দুটি পরস্পর লম্ব ।

∠QPR = 90° [ অর্ধবৃত্তস্থ কোণ ]             

∴ QR বৃত্তের ব্যাস ।

∴ OR ব্যাসের দৈর্ঘ্য =2✕ ব্যাসার্ধ= 2r সেমি.[উত্তর]

(iv) AOB বৃত্তের একটি ব্যাস । C বৃত্তের ওপর একটি বিন্দু । ∠OBC = 60° হলে ∠OCA এর মাণ নির্ণয় করি ।

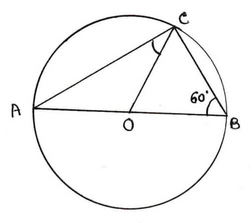
সমাধানঃ

AOB বৃত্তটির একটি ব্যাস ।

C বৃত্তের ওপর একটি বিন্দু ।

∴ ∠ACB = 1 সমকোণ [∵অর্ধবৃত্তস্থ কোণ 1 সমকোণ ]

আবার , ∠OBC = 60°

∴ ∠ABC = 60°

∴ ∠BAC

= 180°-(90°+60°)

= 180°-150°

= 30°

∴ ∠OAC = 30°

∴ ∠OCA = 30° [∵OA =OC,একই বৃত্তের ব্যাসার্ধ][উত্তর]

(v) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস । জ্যা CD এর দৈর্ঘ্য বৃত্তের ব্যাসার্ধের দৈর্ঘ্য – এর সমান । AC ও BD কে বর্ধিত করায় P বিন্দুতে ছেদ করে । ∠APB এর মাণ নির্ণয় করি ।

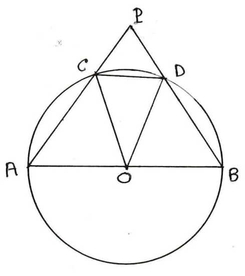
সমাধানঃ

A,D যুক্ত করা হল ।

O বৃত্তের কেন্দ্র এবং AB ব্যাস ।

জ্যা CD এর দৈর্ঘ্য বৃত্তের ব্যাসার্ধের দৈর্ঘ্য – এর সমান

∴ OC=OD=CD

∴ ∆OCD সমবাহু ত্রিভুজ

∴ ∠COD = 60° [ যেহেতু, সমবাহু ত্রিভুজের প্রতিটি কোণের মাণ 60°]

∴ ∠CAD = 30°[ যেহেতু , একই বৃত্তচাপের ওপর  ∠COD কেন্দ্রস্থ কোণ এবং ∠CAD পরিধিস্থ কোণ এবং একই বৃত্তচাপের ওপর কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুণ ]

আবার , ∠ADB অর্ধবৃত্তস্থ কোণ

∴ ∠ADB = 90°

∴ ∠ADP = 90°

∠APD = 180°-(∠ADP+∠PAD)

         = 180°-(90°+30°)

         = 180°-120°

         = 60°

∴ ∠APB = 60°[উত্তর]

Koshe dekhi 7.3 Class 10|বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য কষে দেখি ৭.৩|কষে দেখি 7.3 ক্লাস 10

মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন

ধন্যবাদ । এই POST টি ভাল লাগলে SHARE করার অনুরোধ রইল । এরকম আরও সুন্দর সুন্দর POST পেতে , আমাদের FACEBOOK PAGE টি LIKE করুন।