SN Dey Solution For Class 12 Integration By Parts.সৌরেন্দ্রনাথ দে আংশিক সমাকলন পদ্ধতি ক্লাস ১২।WBCHSE Class 12 Math Solution.WB Board Class 12 Math Solution.SN Dey Maths Solution Class 12.West Bengal Board Class 12 Chaya Math Book Solution Of Class 12.ছায়া গণিত সমাধান দ্বাদশ শ্রেণি (ক্লাস ১২)
Important Links
SN Dey Solution For Class 12 Integration By Parts.সৌরেন্দ্রনাথ দে আংশিক সমাকলন পদ্ধতি ক্লাস ১২।WBCHSE Class 12 Math Solution.WB Board Class 12 Math Solution.SN Dey Maths Solution Class 12.West Bengal Board Class 12 Chaya Math Book Solution Of Class 12.ছায়া গণিত সমাধান দ্বাদশ শ্রেণি (ক্লাস ১২)
আংশিক সমাকলন প্রক্রিয়া (SN Dey Integration By Parts)
একই চলরাশির সাপেক্ষে দুটি অপেক্ষকের গুনফলের সমাকলন নির্ণয় করার জন্য যে পদ্ধতি ব্যবহার করা হয় তাকে আংশিক সমাকলন প্রক্রিয়া বলে ।
আংশিক সমাকলনের সূত্র (SN Dey Integration By Parts)
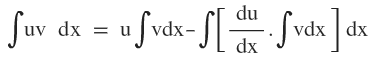
যেখানে u = প্রথম অপেক্ষক , v = দ্বিতীয় অপেক্ষক , (u এবং v উভয়ই x চলরাশির অপেক্ষক )
আংশিক সমাকলনের জন্য প্রথম অপেক্ষক নির্বাচনের নিয়ম:SN Dey Integration By Parts
(i) বীজগাণিতিক ও ত্রিকোণমিতিক অপেক্ষকের গুনফল হলে , বীজগাণিতিক অপেক্ষকটিকে প্রথম অপেক্ষকরূপে গন্য করতে হবে ।
(ii) বীজগাণিতিক ও সূচকীয় হলে, বীজগাণিতিক অপেক্ষকটি প্রথম অপেক্ষকরূপে নির্বাচন করতে হবে ।
(iii) বীজগাণিতিক ও লগারিদমিক অপেক্ষকের গুনফল হলে , বীজগাণিতিক অপেক্ষকটিকে প্রথম অপেক্ষকরূপে নির্বাচন করতে হবে ।
(iv) বীজগাণিতিক ও বিপরীত বৃত্তীয় অপেক্ষকের গুণফল হলে, বিপরীত বৃত্তীয় অপেক্ষকটি প্রথম অপেক্ষক রূপে ধরতে হবে ।
(v) ত্রিকোণমিতিক ও সূচকীয় অপেক্ষকের গুনফল হলে , যে কোনোটিকে প্রথম অপেক্ষকরূপে নির্বাচন করা যাবে ।
(vi) ∫f(x) dx আকারের অর্থাৎ ∫cos-1 x dx বা ∫ logx dx আকারের সমাকলের জন্য cos-1 x বা logx কে সর্বদা প্রথম অপেক্ষক এবং 1 কে দ্বিতীয় অপেক্ষকরূপে ধরে আংশিক সমাকলন পদ্ধতি প্রয়োগ করতে হবে ।
| SN Dey Solution For Class 12 Integration By Parts.সৌরেন্দ্রনাথ দে আংশিক সমাকলন পদ্ধতি ক্লাস ১২।WBCHSE Class 12 Math Solution.WB Board Class 12 Math Solution.SN Dey Maths Solution Class 12.West Bengal Board Class 12 Chaya Math Book Solution Of Class 12.ছায়া গণিত সমাধান দ্বাদশ শ্রেণি (ক্লাস ১২) |
প্রথম অপেক্ষক নির্বাচনের জন্য উপরের নিয়মগুলি LIATE শব্দটি দ্বারা সংক্ষেপে মনে রাখা যায় , যেখানে ,
(i) L এর অর্থ লগারিদমিক ( Logarithmic) অপেক্ষক ।
(ii) I এর অর্থ বিপরীত বৃত্তীয় অপেক্ষক ( Inverse Circular Function) ।
(iii) A এর অর্থ বীজগাণিতিক অপেক্ষক (Algebraic) ।
(iv) T এর অর্থ ত্রিকোণমিতিক অপেক্ষক (Trigonometric) ।
(v) E এর অর্থ সূচকীয় অপেক্ষক ( Exponential ) ।
উদাহরণঃ
(i) ∫x sinx dx
এখানে সমাকলটি অর্থাৎ xsinx হল বীজগাণিতিক অপেক্ষক x এবং ত্রিকোণমিতিক অপেক্ষক sinx এর গুনফল । অর্থাৎ A ও T এর গুনফলের সমাকল নির্ণয় করতে হবে । LIATE শব্দটির অক্ষর বিন্যাস A ও T এর মধ্যে প্রথমে A আছে । সুতরাং বীজগাণিতিক অপেক্ষক অর্থাৎ x কে প্রথম অপেক্ষকরূপে নির্বাচন করতে হবে ।
∴ I =∫x sinx dx
=x∫sinx dx -∫ [d/dx (x) ∫sinx dx ] dx
=-xcosx+∫cosx dx
= -xcosx+sinx+c
[c হল সমাকল ধ্রুবক ]
(ii) ∫xn logx dx
ধরি , I = ∫xn logx dx
সমাকলনটি হল xn logx dx এবং এটি লগারিদমিক অপেক্ষক এবং বীজগাণিতিক অপেক্ষকের গুনফল। LIATE শব্দটির অক্ষর বিন্যাসে A ও L এর মধ্যে L অক্ষরটি প্রথমে আছে । সুতরাং লগারিদমিক অপেক্ষক অর্থাৎ logx কে প্রথম অপেক্ষকরূপে নির্বাচন করতে হবে ।
∴ I = logx∫xn dx-∫[d/dx (logx) ∫xn dx]dx
=logx (x n+1/n+1)-∫1/x .(x n+1/n+1) dx
= logx (x n+1/n+1)- 1/(n+1)∫xn dx
= logx(x n+1/n+1)- {1/(n+1)} (x n+1/n+1)+c
[ c হল সমাকল ধ্রুবক ]
কয়েকটি আদর্শ সমাকলঃ SN Dey Integration By Parts
(i) ∫e ax sinbx dx = eax /(a2+b2) (asinbx-bcosbx) +c
= e ax /√(a2+b2) sin(bx-tan-1 b/a)+c (a,b≠0)
(ii) ∫e ax cosbx dx =eax /(a2+b2) (acosbx+bsinbx) +c
=e ax /√(a2+b2) cos(bx-tan-1 b/a)+c (a,b≠0)
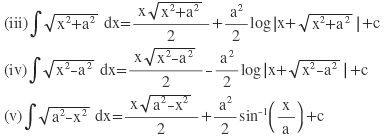
| SN Dey Solution For Class 12 Integration By Parts.সৌরেন্দ্রনাথ দে আংশিক সমাকলন পদ্ধতি ক্লাস ১২।WBCHSE Class 12 Math Solution.WB Board Class 12 Math Solution.SN Dey Maths Solution Class 12.West Bengal Board Class 12 Chaya Math Book Solution Of Class 12.ছায়া গণিত সমাধান দ্বাদশ শ্রেণি (ক্লাস ১২) |
Very good