Koshe Dekhi 23.3 Class 10|ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি কষে দেখি ২৩.৩|কষে দেখি ২৩.৩ ক্লাস ১০| WBBSE Class 10 (Ten)(X)Math Solution Of Chapter 23|Madhyamik Math Solution Of Chapter 23|WB Board Class 10 Math Book Solution In Bengali.
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন ।
Koshe Dekhi 23.3 Class 10|ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি কষে দেখি ২৩.৩|কষে দেখি 23.3 ক্লাস 10



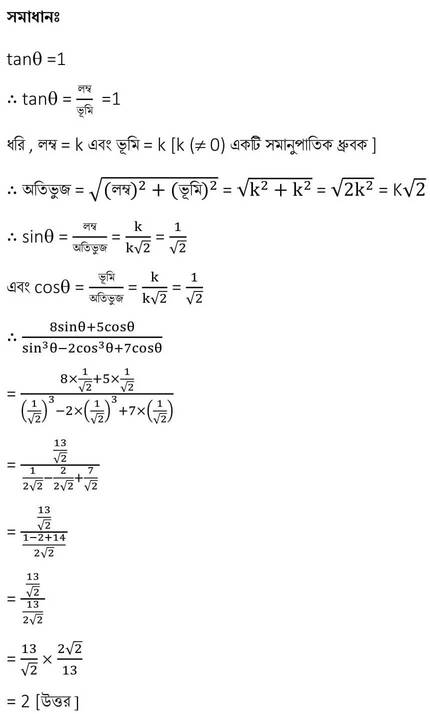
2.(i) cosecϴ এবং tan ϴ– কে sinϴ -এর মাধ্যমে প্রকাশ করি ।
সমাধানঃ
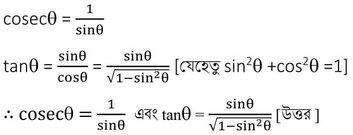
2.(ii) cosecϴ এবং tanϴ -কে cosϴ -এর মাধ্যমে লিখি ।
সমাধানঃ
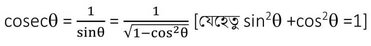
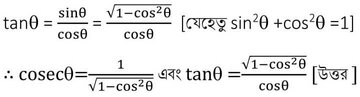
Koshe Dekhi 23.3 Class 10|ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি কষে দেখি ২৩.৩
3. (i) secϴ+tanϴ =2 হলে ,( secϴ-tanϴ)-এর মান নির্ণয় করি ।
সমাধানঃ
আমরা জানি ,
Sec2ϴ -tan2ϴ = 1
বা, (secϴ+tanϴ)(secϴ-tanϴ)=1
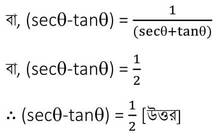
Koshe Dekhi 23.3 Class 10|ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি কষে দেখি ২৩.৩
(ii) cosecϴ -cotϴ = √2 -1 হলে, (cosecϴ +cotϴ) –এর মান হিসাব করে লিখি ।
সমাধানঃ
আমরা জানি ,
Cosec2ϴ -cot2ϴ =1
বা, (cosecϴ+cotϴ)(cosecϴ-cotϴ)=1
বা, (cosecϴ+cotϴ)✕(√2 -1) =1
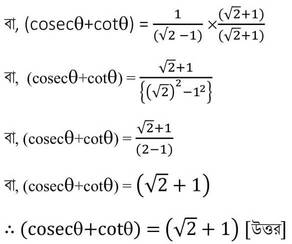
Koshe Dekhi 23.3 Class 10|ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি কষে দেখি ২৩.৩
(iii) sinϴ+cosϴ =1 হলে, sinϴ✕cosϴ-এর মান হিসাব করে লিখি ।
সমাধানঃ
আমরা জানি ,
Sin2ϴ +cos2ϴ=1
বা, (sinϴ+cosϴ)2 -2sinϴ✕cosϴ =1
বা, (1)2 -2 sinϴ✕cosϴ=1
বা, 1 – 2sinϴ✕cosϴ =1
বা, – 2sinϴ✕cosϴ =0
বা, sinϴ✕cosϴ = 0
∴ sinϴ✕cosϴ = 0 [উত্তর]
(iv) tanϴ+cotϴ =2 হলে, (tanϴ-cotϴ) এর মান হিসাব করে লিখি ।
সমাধানঃ
tanϴ+cotϴ =2
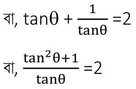
বা, tan2ϴ +1 =2tanϴ
বা, tan2ϴ -2tanϴ+1 =0
বা, (tanϴ-1)2 =0
বা, tanϴ-1=0
বা, tanϴ =1
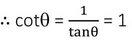
∴ tanϴ -cotϴ = 1-1=0
∴ (tanϴ -cotϴ)-এর মান 0 [উত্তর]
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন ।

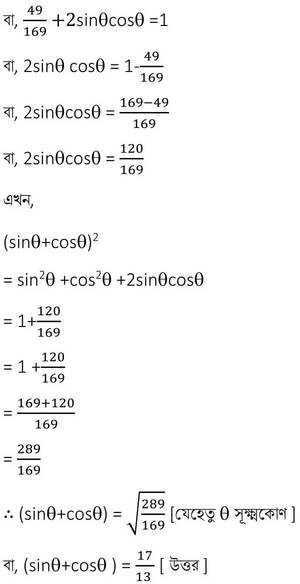

সমাধানঃ
(sinϴ+cosϴ)2 = sin2ϴ+2sinϴcosϴ+cos2ϴ
বা, (sinϴ+cosϴ)2 = (sin2ϴ+cos2ϴ)+2sinϴcosϴ
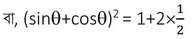
বা, (sinϴ+cosϴ)2 = 2
বা, (sinϴ+cosϴ) = √2 [যেহেতু ϴ সূক্ষ্মকোণ ]
∴ (sinϴ+cosϴ) = √2 [উত্তর]


(viii) cosecϴ+cotϴ = √3 হলে, cosecϴ এবং cotϴ উভয়ের মান নির্ণয় করি ।
সমাধানঃ
cosecϴ +cotϴ= √3 — (i)
আবার , cosec2ϴ -cot2ϴ =1
বা, (cosecϴ+cotϴ)(cosecϴ-cotϴ)=1
বা, √3 ✕ (cosecϴ-cotϴ)=1
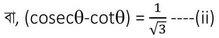
(i) নং ও (ii) নং সমীকরণ যোগ করে পাই ,
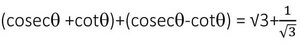


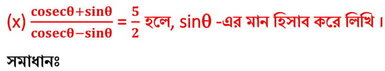



সমাধানঃ
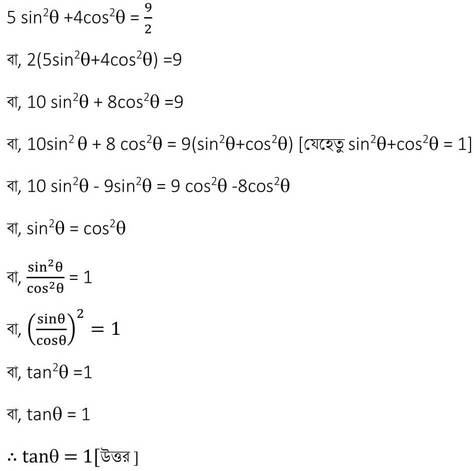

সমাধানঃ
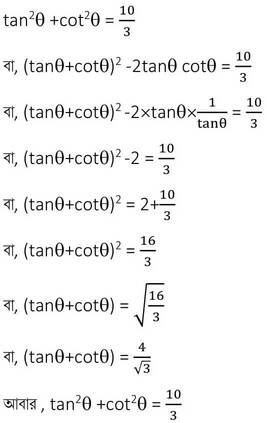
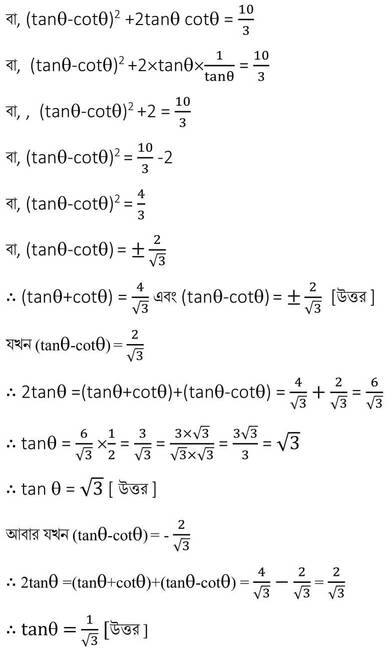

4. (i) PQR ত্রিভুজে ∠Q সমকোণ । PR = √5 একক এবং একক হলে , cosP –cosR –এর মান নির্ণয় করি ।
সমাধানঃ
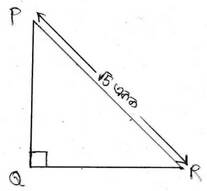
PQR ত্রিভুজে ∠Q সমকোণ এবং PR = √5 একক
∠P এর সাপেক্ষে PQ ভূমি এবং PR অতিভুজ ।

(ii) XYZ ত্রিভুজে ∠Y সমকোণ । XY = 2√3 একক এবং XZ-YZ =2 একক হলে ,(secX-tanX) –এর মান নির্ণয় কর ।
সমাধানঃ
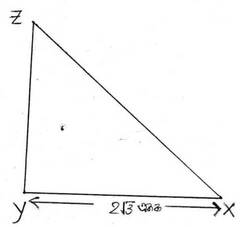
XYZ ত্রিভুজে ∠Y সমকোণ এবং XY = 2√3 একক ।
∠X এর সাপেক্ষে YZ লম্ব এবং XY ভূমি এবং XZ অতিভুজ
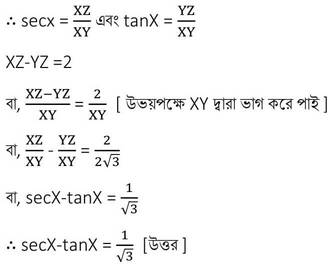
5. সম্পর্কগুলি থেকে ‘ϴ’ অপনয়ন করিঃ
(i) x = 2sinϴ , y = 3cosϴ
সমাধানঃ
x = 2sinϴ , y = 3cosϴ
∴ x2 = 4sin2ϴ
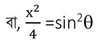
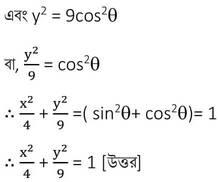
(ii) 5x = 3secϴ , y = 3tanϴ
সমাধানঃ
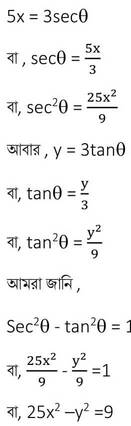
∴ নির্ণেয় সম্পর্ক ( ϴবহির্ভূত ) টি হল 25x2 –y2 =9
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন ।


Koshe Dekhi 23.3 Class 10|ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি কষে দেখি ২৩.৩
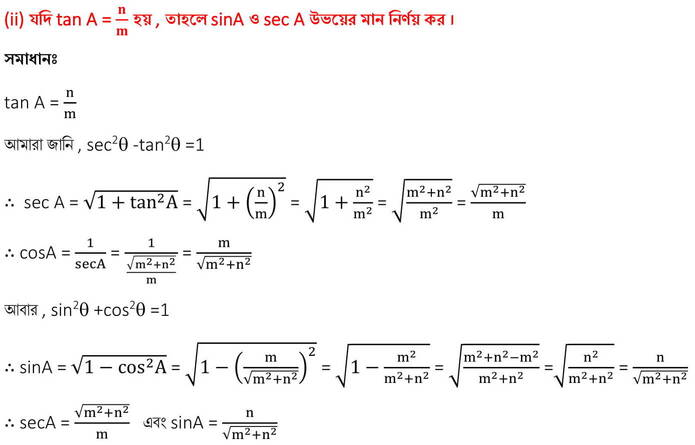



Koshe Dekhi 23.3 Class 10|ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি কষে দেখি ২৩.৩
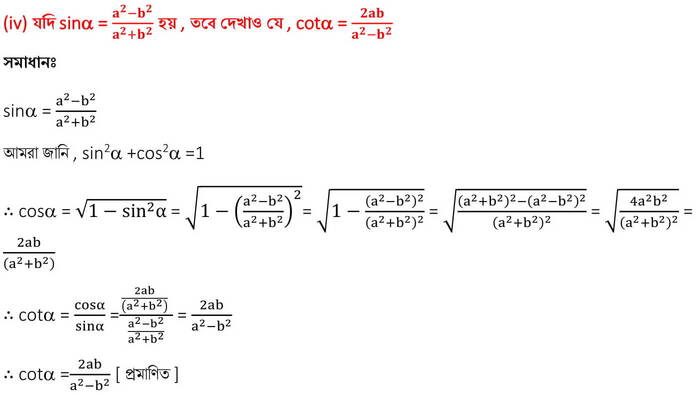

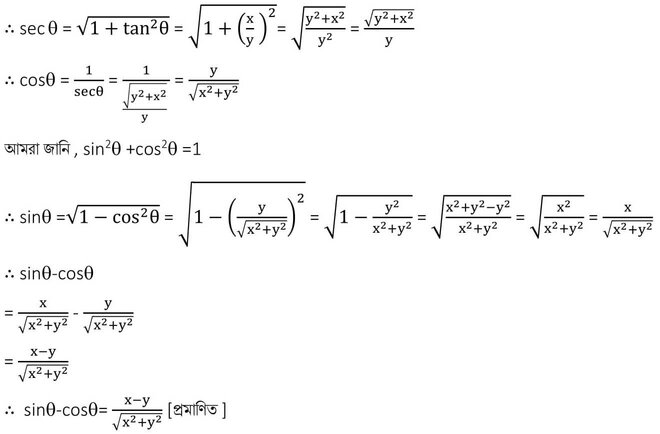



সমাধানঃ
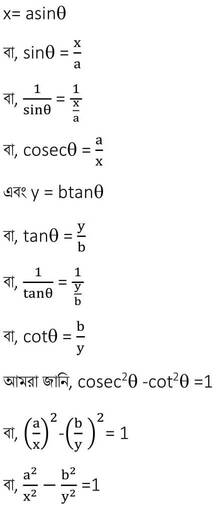
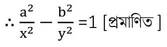
8. যদি sinϴ +sin2ϴ = 1 হয় , তাহলে প্রমাণ করি যে, cos2ϴ +cos4ϴ=1
সমাধানঃ
sinϴ +sin2ϴ = 1
বা, sinϴ= 1- sin2ϴ
বা, sinϴ= cos2ϴ
∴ cos2ϴ +cos4ϴ
= cos2ϴ +(cos2ϴ)2
= sinϴ + sin2ϴ [ যেহেতু sinϴ= cos2ϴ ]
= 1 [যেহেতু sinϴ +sin2ϴ = 1]
∴ cos2ϴ +cos4ϴ =1 [ প্রমাণিত ]
9. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)


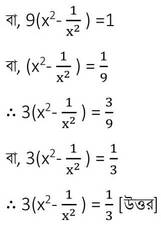
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন

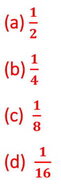
Ans: (b) 1/2
সমাধানঃ
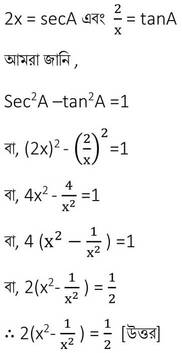
(iii) tanα+cotα =2 হলে, (tan13α +cot13α ) –এর মান
(a) 1
(b) 0
(c ) 2
(d) 1/16
Ans: (c ) 2
সমাধানঃ tanα+cotα =2

(iv) যদি sinϴ -cosϴ = 0 (0° ≤ ϴ≤ 90°) এবং secϴ +cosecϴ =x হয় , তাহলে x এর মান
(a) 1
(b) 2
(c) √2
(d) 2√2
Ans: (d) 2√2
সমাধানঃ
sinϴ -cosϴ = 0
বা, sinϴ = cosϴ
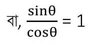
বা, tanϴ = 1
বা, tanϴ =tan45°
বা, ϴ =45°
∴ secϴ +cosecϴ =x
বা, sec 45° +cosec 45° =x
বা, √2 + √2 =x
বা, 2√2 = x [উত্তর]
(v) 2cos3ϴ =1 হলে, ϴ-এর মান
(a) 10°
(b) 15°
(c ) 20°
(d) 30°
Ans: (c ) 20°
সমাধানঃ
2cos3ϴ =1

বা, cos3ϴ = cos 60°
বা, 3ϴ =60°
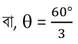
বা, ϴ = 20°[উত্তর]
(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখিঃ
(i) যদি , 0° ≤ α ≤ 90° হয় , তাহলে (sec2α+cos2α) –এর সর্বনিম্ন মান 2
উত্তরঃ সত্য
সমাধানঃ
(sec2α+cos2α)
= (secα -cosα)2 + 2secα cosα
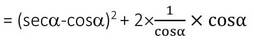
= (secα-cosα)2 + 2
এখন (secα-cosα)2 একটি পূর্ণবর্গ রাশি
∴(secα-cosα)2 -এর সর্বনিম্ন মান 0
∴ (sec2α+cos2α) –এর সর্বনিম্ন মান 2 [উত্তর]
(ii) (cos 0°✕cos1°✕ cos2° ✕cos3°✕……….✕cos90°) –এর মান 1
উত্তরঃ মিথ্যা
সমাধানঃ (cos 0° ✕ cos1°✕ cos2° ✕ cos3° ✕……….✕cos90°) = 0 [যেহেতু cos90° = 0 ]
(C ) শূন্যস্থান পূরণ করিঃ



মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
10. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
(i) যদি r cosϴ =2√3 , rsinϴ = 2 এবং 0°≤ ϴ≤90° হয় ,তাহলে r এবং ϴ উভয়ের মান নির্ণয় করি ।
সমাধানঃ
r cosϴ =2√3
বা, r2 cos2ϴ = 12 [ উভয়পক্ষে বর্গ করে পাই ]
আবার , rsinϴ = 2
বা, r2 sin2ϴ =4 [ উভয়পক্ষে বর্গ করে পাই ]
∴ r2 sin2ϴ + r2 cos2ϴ=12+4
বা, r2 (sin2ϴ+cos2ϴ) =16 [ যেহেতু (sin2ϴ+cos2ϴ) =1]
বা, r2 =(4)2
বা, r = 4

(ii) যদি (sinA+sinB) =2 হয় , যেখানে 0° ≤ A≤ 90° এবং 0° ≤ B ≤ 90° ,তাহলে (cosA+cosB) –এর মান নির্ণয় করি ।
সমাধানঃ 0≤sinA≤1 এবং 0≤ sinB ≤ 1 [যেহেতু 0° ≤ A≤ 90° এবং 0° ≤ B ≤ 90° ]
∴ (sinA+sinB) =1+1
∴ sinA = 1
বা, sinA = sin90°
বা, A = 90°
আবার , sinB = 1
বা, sinB = sin90°
বা, B = 90°
∴ cosA +cosB
= cos90°+cos90°
= 0 [উত্তর ]
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন ।
(iii) যদি 0° < ϴ <90° হয় ,তাহলে 9tan2ϴ +4cot2ϴ -এর সর্বনিম্ন মান নির্ণয় কর ।
সমাধানঃ
9tan2ϴ +4cot2ϴ
= (3tanϴ)2 +(2cotϴ)2
= (3tanϴ-2cotϴ)2 + 2 ✕ 3tanϴ ✕ 2cotϴ
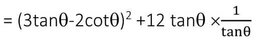
= (3tanϴ-2cotϴ)2 +12
(3tanϴ-2cotϴ)2 – একটি পূর্ণবর্গ রাশি
∴ (3tanϴ-2cotϴ)2 –এর সর্বনিম্ন মান 0
∴ 9tan2ϴ +4cot2ϴ এর সর্বনিম্ন মান 12 [উত্তর]
(iv) (sin6α+cos6α+3sin2αcos2α)-এর মান নির্ণয় করি ।
সমাধানঃ
(sin6α+cos6α+3sin2αcos2α )
= (sin2α)3 +(cos2α)3 +3 sin2αcos2α (sin2α+cos2α) [যেহেতু (sin2α+cos2α) =1]
= (sin2α+cos2α)3 [যেহেতু (a+b)3 =a3+b3+3ab(a+b)]
= (1)3 [যেহেতু sin2 α+cos2α= 1]
= 1 [উত্তর ]
Koshe Dekhi 23.3 Class 10|ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি কষে দেখি ২৩.৩
(v) যদি cosec2ϴ =2cotϴ এবং 0°<ϴ<90° হয় ,তাহলে ϴ-এর মান নির্ণয় করি ।
সমাধানঃ
cosec2ϴ =2cotϴ
বা, 1+cot2ϴ = 2cotϴ [যেহেতু cose2ϴ -cot2ϴ =1 ]
বা, cot2ϴ -2cotϴ +1=0
বা, (cotϴ-1)2 = 0
বা, (cotϴ-1)=0
বা, cotϴ = 1
বা, cotϴ =cot45°
বা, ϴ =45°
∴ ϴ =45° [উত্তর ]
Thanku for the help
Thank you 👍😊😊
Thank you for your help