রাশিবিজ্ঞান কষে দেখি 26.2|Koshe Dekhi 26.2 Class 10|মাধ্যমিক রাশিবিজ্ঞান সমাধান কষে দেখি ২৬.২ |WBBSE Madhyamik Ganit Prakash Somadhan Class 10(Ten)(X) Koshe Dekhi 26.2.
রাশিবিজ্ঞান কষে দেখি 26.2|Koshe Dekhi 26.2 Class 10
কষে দেখি – 26.2
1. মধুবাবুর দোকানে গত সপ্তাহের প্রতিদিনের বিক্রয়লব্ধ অর্থ (টাকায় ) হল , 107 , 210, 92 , 52, 113, 75 , 195 ; বিক্রয়লব্ধ অর্থের মধ্যমা নির্ণয় করি ।
সমাধানঃ
মধুবাবুর দোকানের গত সপ্তাহের প্রতিদিনের বিক্রয়লব্ধ অর্থ মানের উরদ্ধক্রমে সাজিয়ে পাই ,
52, 75, 92, 107, 113, 195, 210
এক্ষেত্রে , n = 7 ( অযুগ্ম )
∴ বিক্রয়লব্ধ অর্থের মধ্যমা = (n+1)/2 তম মান
= (7+1)/2 তম মান
= 8/2 তম মান
= 4 তম মান
= 107 টাকা
2. কিছু পশুর বয়স হলও (বছরে ) 6 , 10, 5, 4 , 9 ,11 , 20 , 18 ; বয়স এর মধ্যমা নির্ণয় করি ।
সমাধানঃ
পশুর বয়স ( বছরে) মানের ঊর্ধ্বক্রমে সাজিয়ে পাই ,
4 ,5 ,6 ,9 ,10 ,11 , 18 ,20
এক্ষেত্রে , n = 8 ( যুগ্ম )
∴ মধ্যমা = ½ [ (n/2) তম পদ + {(n/2)+1} তম পদ ]
= ½ [ (8/2) তম পদ + {(8/2)+1} তম পদ ]
= ½ ( 4 তম পদ + 5 তম পদ )
= ½ (9 + 10)
= ½ × 19
= 9.5 বছর
রাশিবিজ্ঞান কষে দেখি 26.2|Koshe Dekhi 26.2 Class 10
3. 14 জন ছাত্রের গড় বয়স হলও 42 , 51 , 56 , 45, 62, 59, 50, 52, 55, 64, 45, 54, 58, 60 ; প্রাপ্ত নম্বরের মধ্যমা নির্ণয় করি ।
সমাধানঃ
14 জন ছাত্রের প্রাপ্ত নম্বর মানের ঊর্ধ্ব ক্রমে সাজিয়ে পাই ,
42,45,45,50,51,52,54,55,56,58,59,60,62,64
এক্ষেত্রে , n = 14 ( যুগ্ম )
∴ নির্ণেয় মধ্যমা
= ½ [ (n/2) তম পদ + {(n/2)+1} তম পদ ]
= ½ [ (14/2) তম পদ + {(14/2)+1} তম পদ ]
= ½ ( 7 তম পদ + 8 তম পদ )
= ½ (54 + 55)
= ½ × 109
= 54.5
4. আজ আমাদের পাড়ার ক্রিকেট খেলায় আমাদের স্কোর হলো ,
| 7 | 9 | 10 | 11 | 11 | 8 | 7 | 7 | 10 | 6 | 9 |
| 7 | 9 | 9 | 6 | 6 | 8 | 8 | 9 | 8 | 7 | 8 |
ক্রিকেট খেলায় আমাদের স্কোরের মধ্যমা নির্ণয় করি ।
সমাধানঃ
খেলার স্কোর গুলি মানের উর্দ্ধক্রমে সাজিয়ে পাই ,
6,6,6,7,7,7,7,7,8,8,8,8,8,9,9,9,9,9,10,10,11,11 .
এক্ষেত্রে , n = 22 ( যুগ্ম )
∴ নির্ণেয় মধ্যমা
= ½ [ (n/2) তম পদ + {(n/2)+1} তম পদ ]
= ½ [ (22/2) তম পদ + {(22/2)+1} তম পদ ]
= ½ ( 11 তম পদ + 12 তম পদ )
= ½ (8 + 8)
= 8 ( উত্তর )
রাশিবিজ্ঞান কষে দেখি 26.2|Koshe Dekhi 26.2 Class 10
5. নীচের 70 জন ছাত্রের ওজনের পরিসংখ্যা বিভাজন ছক থেকে ওজনের মধ্যমা নির্ণয় করি ।
| ওজন | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| ছাত্র সংখ্যা | 4 | 6 | 8 | 14 | 12 | 10 | 11 | 5 |
সমাধানঃ
প্রদত্ত তথ্য গুলির জন্য পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,
| ওজন ( কিগ্রা ) | ছাত্রসংখ্যা ( পরিসংখ্যা ) | ক্রমযৌগিক পরিসংখ্যা ( ক্ষুদ্রতর সূচক ) |
| 43 | 4 | 4 |
| 44 | 6 | 10 |
| 45 | 8 | 18 |
| 46 | 14 | 32 |
| 47 | 12 | 44 |
| 48 | 10 | 54 |
| 49 | 11 | 65 |
| 50 | 5 | 70 = n |
এখানে , n = 70 ( যুগ্ম )
∴ নির্ণেয় মধ্যমা
= ½ [ (n/2) তম পদ + {(n/2)+1} তম পদ ]
= ½ [ (70/2) তম পদ + {(70/2)+1} তম পদ ]
= ½ ( 35 তম পদ + 36 তম পদ )
= ½ (47 + 47)
= 47
∴ ছাত্রছাত্রী দের ওজনের মধ্যমা = 47 কিগ্রা ।
রাশিবিজ্ঞান কষে দেখি 26.2|Koshe Dekhi 26.2 Class 10
6. নলের ব্যাসের দৈর্ঘ্যের ( মিমি.) পরিসংখ্যা বিভাজন ছক থেকে ব্যাসের দৈর্ঘ্যের মধ্যমা নির্ণয় করি ।
| ব্যাসের দৈর্ঘ্য | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| পরিসংখ্যা | 3 | 4 | 10 | 15 | 25 | 13 | 6 | 4 |
সমাধানঃ
প্রদত্ত তথ্য থেকে পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,
| ব্যাসের দৈর্ঘ্য | পরিসংখ্যা | ক্রমযৌগিক পরিসংখ্যা ( ক্ষুদ্রতর সূচক ) |
| 18 | 3 | 3 |
| 19 | 4 | 7 |
| 20 | 10 | 17 |
| 21 | 15 | 32 |
| 22 | 25 | 57 |
| 23 | 13 | 70 |
| 24 | 6 | 76 |
| 25 | 4 | 80 = n |
এক্ষেত্রে , n = 80 ( যুগ্ম )
∴ নির্ণেয় মধ্যমা
= ½ [ (n/2) তম পদ + {(n/2)+1} তম পদ ]
= ½ [ (80/2) তম পদ + {(80/2)+1} তম পদ ]
= ½ ( 40 তম পদ + 41 তম পদ )
= ½ (22 + 22)
= 22
∴ নলের ব্যাসের দৈর্ঘ্যের মধ্যমা = 22 মিমি .
রাশিবিজ্ঞান কষে দেখি 26.2|Koshe Dekhi 26.2 Class 10
7. মধ্যমা নির্ণয় করিঃ-
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| f | 7 | 44 | 35 | 16 | 9 | 4 | 1 |
সমাধানঃ
প্রদত্ত তথ্য গুলির জন্য পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,
| চলরাশি (X) | পরিসংখ্যা ( f ) | ক্রমযৌগিক পরিসংখ্যা ( ক্ষুদ্রতর সূচক ) |
| 0 | 7 | 7 |
| 1 | 44 | 51 |
| 2 | 35 | 86 |
| 3 | 16 | 102 |
| 4 | 9 | 111 |
| 5 | 4 | 115 |
| 6 | 1 | 116 = n |
এক্ষেত্রে , n = 116 ( যুগ্ম )
∴ নির্ণেয় মধ্যমা
= ½ [ (n/2) তম পদ + {(n/2)+1} তম পদ ]
= ½ [ (116/2) তম পদ + {(116/2)+1} তম পদ ]
= ½ ( 58 তম পদ + 59 তম পদ )
= ½ (2 + 2)
= 4 /2
= 2 ( উত্তর )
রাশিবিজ্ঞান কষে দেখি 26.2|Koshe Dekhi 26.2 Class 10
8. আমাদের 40 জন শিক্ষার্থীর প্রতি সপ্তাহে টিফিন খরচের ( টাকায়) পরিসংখ্যা হলো ,
| টিফিন খরচ ( টাকায় ) | 35-40 | 40-45 | 45-50 | 50-55 | 55-60 | 60-65 | 65-70 |
| শিক্ষার্থীর | 3 | 5 | 6 | 9 | 7 | 8 | 2 |
সমাধানঃ
পরিসংখ্যা বিভাজন তালিকা টি হলো ,
| টিফিন খরচ ( টাকা ) | শিক্ষার্থীর সংখ্যা ( পরিসংখ্যা ) | ক্রমযৌগিক পরিসংখ্যা ( ক্ষুদ্রতর সূচক ) |
| 35-40 | 3 | 3 |
| 40-45 | 5 | 8 |
| 45-50 | 6 | 14 |
| 50-55 | 9 | 23 |
| 55-60 | 7 | 30 |
| 60-65 | 8 | 38 |
| 65-70 | 2 | 40 = n |
এক্ষেত্রে , n = 40 (যুগ্ম )
∴ n /2 = 40/2 =20
20 এর থেকে ঠিক বেশি পরিসংখ্যা বিশিষ্ট শ্রেণীটি হলো (50-55)
∴ মধ্যমা শ্রেণীটি হলো = 50 – 55
মধ্যমা নির্ণয়ের সূত্র টি হলো ,
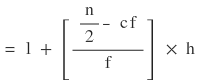
যেখানে ,
l = মধ্যমা শ্রেণীর নিম্ন শ্রেণী সীমানা ।
n = মোট পরিসংখ্যা ।
f = মধ্যমা শ্রেণীর পরিসংখ্যা ।
h = মধ্যমা শ্রেণীর শ্রেণী দৈর্ঘ্য ।
cf = মধ্যমা শ্রেণীর পূর্বের শ্রেণীর ক্রমযৌগিক পরিসংখ্যা ।
∴ নির্ণেয় মধ্যমা
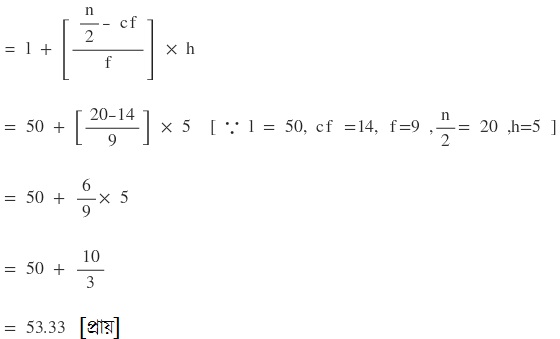
উত্তরঃ 53.33 টাকা ।
9.নীচের তথ্য থেকে ছাত্রদের উচ্চতার মধ্যমা নির্ণয় করি ।
| উচ্চতা ( সেমি) | 135-140 | 140-145 | 145-150 | 150-155 | 155-160 | 160-165 | 165-170 |
| ছাত্রদের সংখ্যা | 6 | 10 | 19 | 22 | 20 | 16 | 7 |
সমাধানঃ
প্রদত্ত তথ্য থেকে পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,
| উচ্চতা (সেমি) | ছাত্রদের সংখ্যা | ক্রমযৌগিক পরিসংখ্যা ( ক্ষুদ্রতর সূচক ) |
| 135-140 | 6 | 6 |
| 140-145 | 10 | 16 |
| 145-150 | 19 | 35 |
| 150-155 | 22 | 57 |
| 155-160 | 20 | 77 |
| 160-165 | 16 | 93 |
| 165-170 | 7 | 100=n |
এখা্নে , n = 100
∴ n/2 = 50
50 এর থেকে ঠিক বেশি পরিসংখ্যা বিশিষ্ট শ্রেণী টি হলো (150-155)
∴ মধ্যমা শ্রেণীটি হলো = 150 – 155
মধ্যমা নির্ণয়ের সূত্র টি হলো,
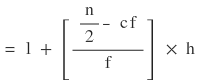
l = মধ্যমা শ্রেণীর নিম্ন শ্রেণী সীমানা ।
n = মোট পরিসংখ্যা ।
f = মধ্যমা শ্রেণীর পরিসংখ্যা ।
h = মধ্যমা শ্রেণীর শ্রেণী দৈর্ঘ্য ।
cf = মধ্যমা শ্রেণীর পূর্বের শ্রেণীর ক্রমযৌগিক পরিসংখ্যা ।
∴ নির্ণেয় মধ্যমা

∴ ছাত্রদের উচ্চতার মধ্যমা 153.41 সেমি.।
রাশিবিজ্ঞান কষে দেখি 26.2|Koshe Dekhi 26.2 Class 10
10. নীচের পরিসংখ্যা বিভাজন থেকে তথ্যটির মধ্যমা নির্ণয় করি ।
| শ্রেণী সীমানা | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 |
| পরিসংখ্যা | 4 | 7 | 10 | 15 | 10 | 8 | 5 |
সমাধান ঃ
প্রদত্ত তথ্য থেকে পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,
| শ্রেণী সীমানা | পরিসংখ্যা | ক্রম-যৌগিক পরিসংখ্যা ( ক্ষুদ্রতর সূচক ) |
| 0-10 | 4 | 4 |
| 10-20 | 7 | 11 |
| 20-30 | 10 | 21 |
| 30-40 | 15 | 36 |
| 40-50 | 10 | 46 |
| 50-60 | 8 | 54 |
| 60-70 | 5 | 59 = n |
এখানে, n = 59
∴ n/2 = 59/2 = 29.5
29.5 এর থেকে ঠিক বেশি পরিসংখ্যা বিশিষ্ট শ্রেণীটি হলো (30-40)
∴ মধ্যমা শ্রেণীটি হলো = 30 – 40
∴ মধ্যমা নির্ণয়ের সূত্র টি হলো
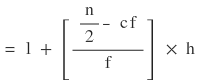
l = মধ্যমা শ্রেণীর নিম্ন শ্রেণী সীমানা ।
n = মোট পরিসংখ্যা ।
f = মধ্যমা শ্রেণীর পরিসংখ্যা ।
h = মধ্যমা শ্রেণীর শ্রেণী দৈর্ঘ্য ।
cf = মধ্যমা শ্রেণীর পূর্বের শ্রেণীর ক্রমযৌগিক পরিসংখ্যা ।
∴ নির্ণেয় মধ্যমা
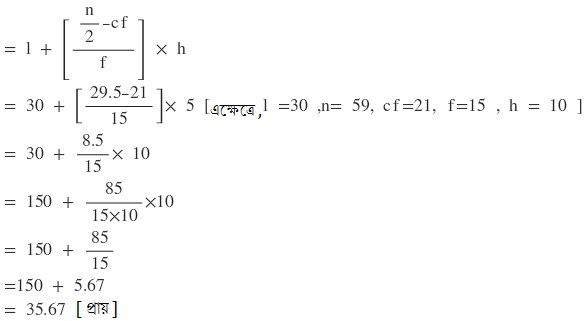
রাশিবিজ্ঞান কষে দেখি 26.2|Koshe Dekhi 26.2 Class 10
11. নীচের তথ্যের মধ্যমা নির্ণয় করি ঃ
| শ্রেণী সীমানা | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 | 30-35 | 35-40 | 40-45 |
| পরিসংখ্যা | 5 | 6 | 15 | 10 | 5 | 4 | 3 | 2 |
সমাধান ঃ
প্রদত্ত তথ্য থেকে পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,
| শ্রেণী – সীমানা | পরিসংখ্যা | ক্রম- যৌগিক পরিসংখ্যা ( ক্ষুদ্রতর সূচক ) |
| 5-10 | 5 | 5 |
| 10-15 | 6 | 11 |
| 15-20 | 15 | 26 |
| 20-25 | 10 | 36 |
| 25-30 | 5 | 41 |
| 30-35 | 4 | 45 |
| 35-40 | 3 | 48 |
| 40-45 | 2 | 50 = n |
এখানে, n = 50
∴ n/2 = 50/2 = 25
25 এর থেকে ঠিক বেশি পরিসংখ্যা বিশিষ্ট শ্রেণীটি হলো (15-20)
∴ মধ্যমা শ্রেণী টি হলো = 15 – 20
∴ মধ্যমা নির্ণয়ের সূত্র টি হলো
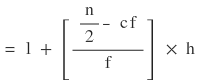
l = মধ্যমা শ্রেণীর নিম্ন শ্রেণী সীমানা ।
n = মোট পরিসংখ্যা ।
f = মধ্যমা শ্রেণীর পরিসংখ্যা ।
h =মধ্যমা শ্রেণীর শ্রেণী দৈর্ঘ্য ।
cf = মধ্যমা শ্রেণীর পূর্বের শ্রেণীর ক্রমযৌগিক পরিসংখ্যা ।
∴ নির্ণেয় মধ্যমা
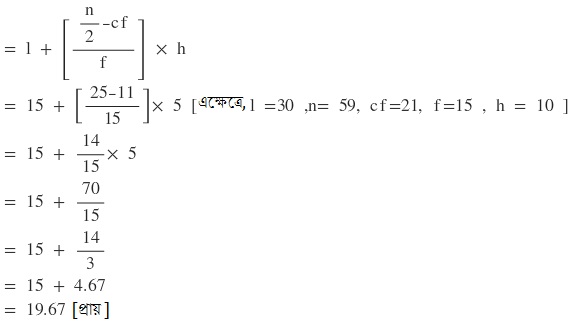
রাশিবিজ্ঞান কষে দেখি 26.2|Koshe Dekhi 26.2 Class 10
12. নীচের তথ্যের মধ্যমা নির্ণয় করি ।
| শ্রেণী সীমা | 1-5 | 6-10 | 11-15 | 16-20 | 21-25 | 26-30 | 31-35 |
| পরিসংখ্যা | 2 | 3 | 6 | 7 | 5 | 4 | 3 |
সমাধানঃ
প্রদত্ত পরিসংখ্যা বিভাজনের ছকের শ্রেণীগুলি শ্রেণী অন্তর্ভুক্ত গঠনে আছে ।
শ্রেণী বহির্ভূত পদ্ধতিতে পরিসংখ্যা বিভাজনের তালিকা তৈরি করি ,
Adjustment factor = (61-60)/2 = ½ = 0.5
1-0.5=0.5 ,5+0.5=5.5 ; 6-0.5=5.5 ,10+0.5=10.5 …………
এই ভাবে গণনা করে শ্রেণী বহির্ভুত পদ্ধতিতে পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,
| শ্রেণী- সীমা | শ্রেণী -সীমানা | পরিসংখ্যা | ক্রম-যৌগিক পরিসংখ্যা ( ক্ষুদ্রতর সূচক ) |
| 1-5 | 0.5-5.5 | 2 | 2 |
| 6-10 | 5.5-10.5 | 3 | 5 |
| 11-15 | 10.5-15.5 | 6 | 11 |
| 16-20 | 15.5-20.5 | 7 | 18 |
| 21-25 | 20.5-25.5 | 5 | 23 |
| 26-30 | 25.5-30.5 | 4 | 27 |
| 31-35 | 30.5-35.5 | 3 | 30 = n |
এখানে , n = 30
∴ n/2 = 30/2 = 15
15 এর থেকে ঠিক বেশি পরিসংখ্যা বিশিষ্ট শ্রেণীটি হলো (15.5-20.5)
∴ মধ্যমা শ্রেণীটি হলো = 15.5 – 20.5
∴ মধ্যমা নির্ণয়ের সূত্র টি হলো
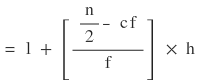
l = মধ্যমা শ্রেণীর নিম্ন শ্রেণী সীমানা ।
n = মোট পরিসংখ্যা ।
f = মধ্যমা শ্রেণীর পরিসংখ্যা ।
h = মধ্যমা শ্রেণীর শ্রেণী দৈর্ঘ্য ।
cf = মধ্যমা শ্রেণীর পূর্বের শ্রেণীর ক্রমযৌগিক পরিসংখ্যা ।
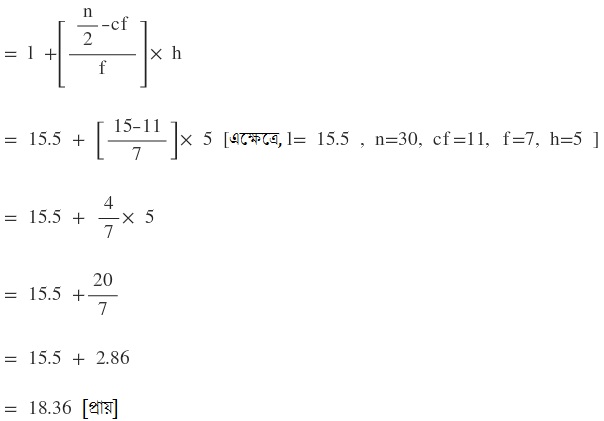
সুতরাং নির্ণেয় মধ্যমা = 18.36 ।
13. নীচের তথ্যের মধ্যমা নির্ণয় করি ।
| শ্রেণী সীমা | 51-60 | 61-70 | 71-80 | 81-90 | 91-100 | 101-110 |
| পরিসংখ্যা | 4 | 10 | 15 | 20 | 15 | 4 |
সমাধানঃ
প্রদত্ত পরিসংখ্যা বিভাজনের ছকের শ্রেণিগুলি শ্রেণী অন্তর্ভুক্ত গঠনে আছে ।
শ্রেণী বহির্ভূত পরিসংখ্যা বিভাজনের তালিকা তৈরি করি ,
Adjustment factor = (61-60)/2 = ½ = 0.5
51- 0.5 =50 ,60+0.5 = 60.5 ;61 – 0.5 = 60.5 ,70 + 0.5 =70.5………
এই ভাবে গণনা করে শ্রেণী বহির্ভুত পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,
| শ্রেণী- সীমা | শ্রেণী -সীমানা | পরিসংখ্যা | ক্রম-যৌগিক পরিসংখ্যা ( ক্ষুদ্রতর সূচক ) |
| 51-60 | 50.5-60.5 | 4 | 4 |
| 61-70 | 60.5-70.5 | 10 | 14 |
| 71-80 | 70.5-80.5 | 15 | 29 |
| 81-90 | 80.5-90.5 | 20 | 49 |
| 91-100 | 90.5-100.5 | 15 | 64 |
| 101-110 | 100.5-110.5 | 4 | 68 = n |
এখানে , n = 68
∴ n/2 = 68/2 = 34
15 এর থেকে ঠিক বেশি পরিসংখ্যা বিশিষ্ট শ্রেণীটি হলো (80.5-90.5)
∴ মধ্যমা শ্রেণীটি হলো = 80.5-90.5
∴ মধ্যমা নির্ণয়ের সূত্র টি হলো
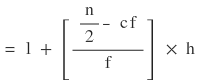
l = মধ্যমা শ্রেণীর নিম্ন শ্রেণী সীমানা ।
n = মোট পরিসংখ্যা ।
f = মধ্যমা শ্রেণীর শ্রেণী দৈর্ঘ্য ।
cf = মধ্যমা শ্রেণীর পূর্বের শ্রেণীর ক্রমযৌগিক পরিসংখ্যা ।

14. নীচের তথ্যের মধ্যমা নির্ণয় করি ঃ
| নম্বর | ছাত্রীদের সংখ্যা |
| 10- এর কম | 12 |
| 20-এর কম | 22 |
| 30- এর কম | 40 |
| 40- এর কম | 60 |
| 50- এর কম | 72 |
| 60- এর কম | 87 |
| 70- এর কম | 102 |
| 80- এর কম | 111 |
| 90- এর কম | 120 |
সমাধান ঃ
শ্রেণীটির পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,
| শ্রেণী -সীমানা | পরিসংখ্যা | ক্রম-যৌগিক পরিসংখ্যা ( ক্ষুদ্রতর সূচক ) |
| 0-10 | 12 | 12 |
| 10-20 | 10 | 22 |
| 20-30 | 18 | 40 |
| 30-40 | 20 | 60 |
| 40-50 | 12 | 72 |
| 50-60 | 15 | 87 |
| 60-70 | 15 | 102 |
| 70-80 | 9 | 111 |
| 80-90 | 9 | 120 |
এখানে , n = 120
∴ n/2 = 120 / 2 = 60
60 এর থেকে ঠিক বেশি পরিসংখ্যা বিশিষ্ট শ্রেণীটি হল (40-50)
∴ মধ্যমা শ্রেণীটি হলো = 40-50
∴ মধ্যমা নির্ণয়ের সূত্রটি হল
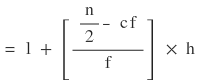
l = মধ্যমা শ্রেণীর নিম্ন শ্রেণী সীমানা ।
n = মোট পরিসংখ্যা ।
f = মধ্যমা শ্রেণীর পরিসংখ্যা ।
h = মধ্যমা শ্রেণীর শ্রেণী দৈর্ঘ্য ।
cf = মধ্যমা শ্রেণীর পূর্বের শ্রেণীর ক্রমযৌগিক পরিসংখ্যা ।
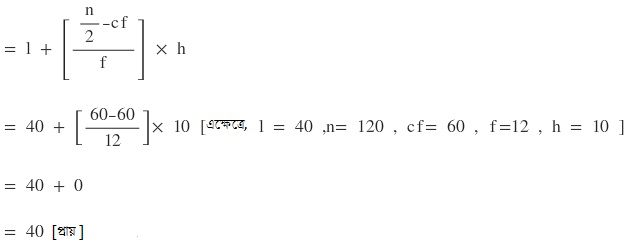
15. নীচের তথ্যের মধ্যমা 32 হলে x ও y এর মান নির্ণয় করি যখন পরিসংখ্যার সমষ্টি 100 ;
| শ্রেণী- সীমানা | পরিসংখ্যা |
| 0-10 | 10 |
| 10-20 | x |
| 20-30 | 25 |
| 30-40 | 30 |
| 40-50 | y |
| 50-60 | 10 |
সমাধানঃ
প্রদত্ত তথ্য থেকে পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,
| শ্রেণী-সীমানা | পরিসংখ্যা | ক্রমযৌগিক পরিসংখ্যা (ক্ষুদ্রতর সূচক ) |
| 0-10 | 10 | 10 |
| 10-20 | X | 10+x |
| 20-30 | 25 | 35+x |
| 30-40 | 30 | 65+x |
| 40-50 | Y | 65+x+y |
| 50-60 | 10 | 75+x+y = n |
এখানে , n = 100 (প্রদত্ত )
শর্তানুসারে ,
75+x+y = 100
বা, x+y = 25 ——– (i)
আবার মধ্যমা = 32 (প্রদত্ত )
সুতরাং মধ্যমা শ্রেণীটি হলো = ( 30 -40 )
এখন মধ্যমা নির্ণয়ের সূত্রটি হলো
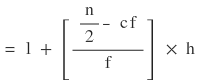
l = মধ্যমা শ্রেণীর নিম্ন শ্রেণী সীমানা ।
n = মোট পরিসংখ্যা ।
f = মধ্যমা শ্রেণীর পরিসংখ্যা ।
h = মধ্যমা শ্রেণীর শ্রেণী দৈর্ঘ্য ।
cf = মধ্যমা শ্রেণীর পূর্বের শ্রেণীর ক্রমযৌগিক পরিসংখ্যা ।
∴ মধ্যমা
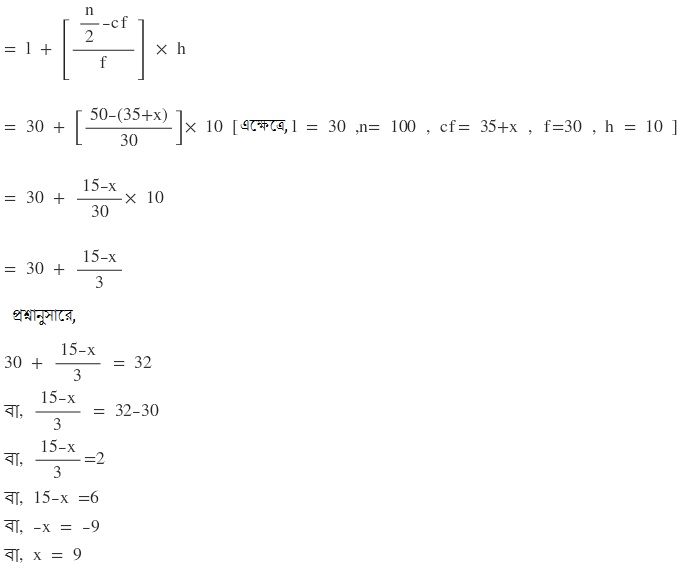
(i) নং সমীকরণে x এর মান বসিয়ে পাই ,
9 + y = 25
বা, y = 25-98
বা, y = 16
∴ x = 9 এবং y = 16 [ উত্তর ]
আরও দেখুনঃ
ধন্যবাদ । এই POST টি ভালো লাগলে SHARE করার অনুরোধ রইল । এইরকম আরও সুন্দর সুন্দর POST পেতে , আমাদের FACEBOOK PAGE টি LIKE করুন।
Very good
খুব ভালো
Very helpful for us !
Thanks for dout clearing 👌😊🤗
Thanks for dout clearing 👌😊🤗
Thanks For dout Clearing ❤🤗
Very good,it is a nice
thanks 🙏👍