কোণ পরিমাপের ধারণা কষে দেখি ২০|Koshe Dekhi 20 Class 10|গণিত প্রকাশ ক্লাস ১০ কষে দেখি ২০|Madhyamik Math Solution Of Chapter 20|WBBSE Class 10 Math Solution Of Chapter 20|Ganit Prokash Class 10 Koshe Dekhi 20
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন ।
কোণ পরিমাপের ধারণা কষে দেখি ২০|Koshe Dekhi 20 Class 10|কষে দেখি 20 ক্লাস 10
জ্যামিতিক কোণ কাকে বলে?
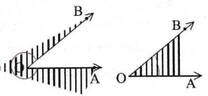
উত্তরঃ পাশের চিত্রে ,O বিন্দু থেকে OA এবং OB রশ্মিদুটি নির্গত হওয়ায় O বিন্দুতে AOB ও প্রবৃদ্ধ কোণ BOA উৎপন্ন হয়েছে , এদের ‘জ্যামিতিক কোণ’ বলা হয় । জ্যামিতিক কোণের ক্ষেত্রে দিক ছাড়া কোণের পরিমাণই মূল বিচার্য বিষয় ।
ত্রিকোণমিতিক কোণ কাকে বলে ?
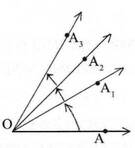
উত্তরঃ পাশের চিত্রে , OA রশ্মির প্রান্তবিন্দু O -কে স্থির রেখে একই তলে ঘড়ির কাঁটার বিপরীত দিকে ঘুরিয়ে রশ্মির OA1 ,OA2 ,OA3 ইত্যাদি অবস্থান পেয়েছি যারা O বিন্দুতে যথাক্রমে ∠AOA1 , ∠AOA2 , ∠AOA3 ইত্যাদি বিভিন্ন কোণ উৎপন্ন করেছে । এই কোণ গুলিকে ত্রিকোণমিতিক কোণ বলা হয় ।
ত্রিকোণমিতিক কোণের ক্ষেত্রে ঘূর্ণায়মান রশ্মির দিক ও তার ফলে সৃষ্ট কোণের পরিমাপ উভয়ই বিচার করা হয় । ঘূর্ণায়মান রশ্মিটি ঘড়ির কাঁটার বিপরীত দিকে ঘুরলে উৎপন্ন কোণটিকে রীতি অনুসারে ধনাত্মক কোণ বলে এবং রশ্মিটি ঘড়ির কাঁটার দিকে ঘুরলে ঋণাত্মক কোণ সৃষ্টি হয় ।
জ্যামিতিক কোণের সর্বনিম্ন ও সর্বাধিক পরিমাপ হয় যথাক্রমে 0° এবং 360°; কিন্তু ত্রিকোণমিতিক কোণের পরিমাপ হল 0° থেকে 360° ছাড়াও 0° এর কম যেকোনো পরিমাপ এবং 360° এর বেশী যেকোনো পরিমাপ হতে পারে ।
কোণ পরিমাপের ধারণা কষে দেখি ২০|Koshe Dekhi 20 Class 10
ত্রিকোণমিতিক কোণ কি কি পদ্ধতিতে পরিমাপ করা হয় ও কি কি ?
উত্তরঃ ত্রিকোণমিতিক কোণ দুটি পদ্ধতিতে পরিমাপ করা হয় (i) ষষ্টিক পদ্ধতি (ii) বৃত্তীয় পদ্ধতি ।
ষষ্টিক পদ্ধতি বলতে কি বোঝো ?
উত্তরঃ দুটি পরস্পরছেদী সরলরেখা একে অপরের ওপর লম্বভাবে দাঁড়ালে যে কোণ তৈরি হয় তাকে সমকোণ বলে । এই পদ্ধতিতে এক সমকোণ কে 90 টি সমান ভাগে বিভক্ত করা হয় এবং তার প্রতিটি ভাগকে এক ডিগ্রি (1°) বলা হয় এবং এই কারনেই এক সমকোণ = 90° ; 1 ডিগ্রিকে পুনরায় 60 টি সমান ষষ্টিক মিনিটে ও প্রতি মিনিটকে 60 টি ষষ্টিক সেকেন্ডে বিভক্ত করা হয় ।
∴ পেলাম , 1 সমকোণ = 90°
1° = 60′ (মিনিট)
1′ = 60” (সেকেন্ড)
কোণ পরিমাপের ধারণা কষে দেখি ২০|Koshe Dekhi 20 Class 10
বৃত্তীয় পদ্ধতি বলতে কি বোঝো ?
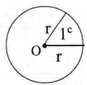
উত্তরঃ একটি বৃত্তে ব্যাসার্ধের দৈর্ঘ্যের সমান দৈর্ঘ্যের বৃত্তচাপ ওই বৃত্তের কেন্দ্রে যে সম্মুখ কোণ উৎপন্ন করে তার পরিমাপকে এক রেডিয়ান বলা হয় এবং লেখা হয় 1c ; যেকোনো একটি বৃত্তের পরিধি এবং ব্যাসের দৈর্ঘ্যের অনুপাত ধ্রুবক ।এই সম্পর্কটির উপর ভিত্তি করে এই পদ্ধতির একক নির্ধারিত হয়েছে ।
প্রমাণ করি 1 রেডিয়ান একটি ধ্রুবক কোণ ।
প্রমাণঃ

1° -এর মান বৃত্তীয় পদ্ধতিতে
সমাধানঃ
$180° = \pi^c$
বা, 1° = $\left(\frac{\pi }{180}\right)^c = \left(\frac{22}{7 \times 180}\right)^c$
$\therefore 1° < 1^c\left[\because \frac{22}{7 \times 180} < 1\right]$
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
কষে দেখি 20 ক্লাস 10
1. নিম্নলিখিত গুলিকে ডিগ্রি , মিনিট ও সেকেন্ডে প্রকাশ করিঃ
(i) 832′
সমাধানঃ
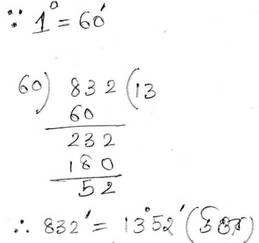
(ii) 6312”
সমাধানঃ
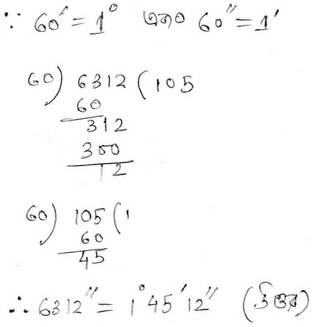
(iii) 375”
সমাধানঃ
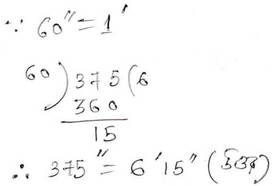
(iv) $27\frac{1}{12}°$
সমাধানঃ
$27\frac{1}{12}°$
= $27° + \left(\frac{1}{12}\right)°$
= $27° + \left(\frac{1}{12} \times 60\right)’$[∵1°=60′]
= $27° 5’$
কোণ পরিমাপের ধারণা কষে দেখি ২০|Koshe Dekhi 20 Class 10
(v) 72.04°
সমাধানঃ
72.04°
=72° +0.4°
= 72° + (.04✕60)’ [যেহেতু 1° =60′]
= 72° + 2.4′
= 72°+ 2′ +0.4′
= 72°2′(0.4✕60)” [যেহেতু 1’=60”]
=72°2’24”
কোণ পরিমাপের ধারণা কষে দেখি ২০|Koshe Dekhi 20 Class 10
2. নিম্ন লিখিতগুলির বৃত্তীয় মান নির্ণয় করঃ
(i) 60°
সমাধানঃ
180° = πc
$\therefore 60° = \frac{\pi }{180} \times 60 = \frac{\pi }{3}$
(ii) 135°
সমাধানঃ
180° = πc
$\therefore 135° = \frac{\pi }{180} \times 135 = \frac{3\pi }{4}$
(iii) -150°
সমাধানঃ
180° = πc
$-150° = \frac{\pi^c}{180} \times ( – 150) = – \frac{5\pi^c}{6}$
(iv) 72°
সমাধানঃ
180° = πc
$\therefore 72° = \frac{\pi^c}{180} \times 72 = \frac{2\pi^c}{5}$
(v) 22°30′
সমাধানঃ
22°30’
= $22°+ \left(\frac{30}{60}\right)°$
= $22° + \left(\frac{1}{2}\right)° $
= $\left(\frac{44 + 1}{2}\right)°$
= $\frac{45}{2}°$
$\because 180° = \pi^c$
$\therefore \frac{45}{2}°=\frac{\pi^c}{180} \times \frac{45}{2} = \frac{\pi^c}{8}$
∴ 22°30’ = $\frac{\pi^c}{8}$
(vi) -62°30′
সমাধানঃ
– 62°30′
= $- \left[62 + \left(\frac{30}{60}\right)\right]°$
= $- \left[62 + \left(\frac{1}{2}\right)\right]° $
= $- \left[\frac{124 + 1}{2}\right]°$
= $- \frac{125}{2}°$
$\because 180°= \pi^c$
$\therefore – \frac{125}{2}°= \frac{\pi^c}{180} \times \frac{125}{2} = -\frac{25\pi^c}{72}$
∴- 62° 30′ = $- \frac{25\pi^c}{72}$
(vii) 52°52’30”
সমাধানঃ
52°52’30”
= $52° + 52′ + \left(\frac{30}{60}\right)’$
= $52° + \left(52 + \frac{1}{2}\right)’$
= $52° + \left(\frac{104 + 1}{2}\right)’$
= $52° + \left(\frac{105}{2}\right)’$
= $52° + \left(\frac{105}{2 \times 60}\right)°$
= $52° + \left(\frac{21}{24}\right)°$
= $\left(\frac{1248 + 21}{24}\right)°$
= $\left(\frac{1269}{24}\right)°$
যেহেতু, $180 = \pi^c$
∴ $\left(\frac{1269}{24}\right)° $
= $\frac{\pi^c}{180} \times \frac{1269}{24}$
= $\frac{47\pi^c}{160}$
∴ 52°52’52” = $\frac{47\pi^c}{160}$
(Viii) 40°16’24”
সমাধানঃ
$40°16’24″$
= $40°+ 16′ + \left(\frac{24}{60}\right)’$
= $40°+ 16′ + \left(\frac{2}{5}\right)’$
= $40°+ \left(16 + \frac{2}{5}\right)’$
= $40°+ \left(\frac{80 + 2}{5}\right)’$
= $40°+ \left(\frac{82}{5}\right)’$
= $40°+ \left(\frac{82}{5 \times 60}\right)°$
= $40° + \frac{41}{150}°$
= $\left(\frac{6000 + 41}{150}\right)°$
= $\frac{6041}{150}°$
যেহেতু, $180° = \pi^c$
$\therefore \frac{6041°}{150} $
= $\frac{\pi^c}{180} \times \frac{6041}{150}$
= $\frac{6041\pi^c}{27000}\therefore 40°16’24″$
= $\frac{6041\pi^c}{27000}$ (উত্তর )
কোণ পরিমাপের ধারণা কষে দেখি ২০|Koshe Dekhi 20 Class 10
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
কোণ পরিমাপের ধারণা কষে দেখি ২০|Koshe Dekhi 20 Class 10
3. ABC –এর AC=BC এবং BC বাহুকে D পর্যন্ত বর্ধিত করলাম । যদি ∠ACD = 144° হয় , তবে ABC ত্রিভুজের প্রতিটি কোণের বৃত্তীয় মান নির্ণয় করি ।
সমাধানঃ
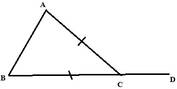
ABC ত্রিভুজের AC =BC
∴ ∠ABC = ∠CAB
এবং BC বাহুকে D পর্যন্ত বর্ধিত করা হলে ,
∠ACD = 144°
∴ ∠ACB = 180°-144° = 36°
∴ ∠ABC = ∠CAB = $\frac{180° – 36°}{2}$ = 72°
∠ACB –এর বৃত্তীয় মান
=$\frac{36{\mathrm{\pi}}^{{\mathrm{c}}}}{180}$
= $\frac{{\mathrm{\pi}}^{{\mathrm{c}}}}{5}$
∠ABC –এর বৃত্তীয় মান
=$\frac{72{\mathrm{\pi}}^{{\mathrm{c}}}}{180}$
= $\frac{2{\mathrm{\pi}}^{{\mathrm{c}}}}{5}$
এবং ∠CAB –এর বৃত্তীয় মান
=$\frac{72{\mathrm{\pi}}^{{\mathrm{c}}}}{180}$
= $\frac{2{\mathrm{\pi}}^{{\mathrm{c}}}}{5}$
কোণ পরিমাপের ধারণা কষে দেখি ২০|Koshe Dekhi 20 Class 10
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন ।
4. একটি সমকোণী ত্রিভুজের সূক্ষ্মকোণ দুটির অন্তর 2π/3 হলে , ষষ্টিক পদ্ধতিতে কোণ দুটির মান লেখ ।
সমাধানঃ ধরি , ABC একটি সমকোণী ত্রিভুজ যার সূক্ষ্মকোণ দুটি হল A এবং C ।
∴ A+C = 90° —(i)[যেহেতু সমকোণী ত্রিভুজের সূক্ষ্মকোণ দুটির সমষ্টি 90° ]
আবার , A-C =$\frac{2{\mathrm{\pi}}}{3}$ [যেহেতু π রেডিয়ান =180°]
বা, A-C = 72° —(ii)
(i) ও (ii) নং সমীকরণদ্বয় যোগ করে পাই ,
A+C+A-C = 90°+72°
বা, 2A = 162°
বা, A =$\frac{162}{2}$
বা, A = 81°
A এর প্রাপ্ত মান (ii) নং সমীকরণের বসিয়ে পাই ,
81°-C = 72°
বা, 81°-72° =C
বা, C = 9°
∴ ষষ্টিক পদ্ধতিতে কোণ দুটির মান 81° এবং 9 ° ।
কোণ পরিমাপের ধারণা কষে দেখি ২০|Koshe Dekhi 20 Class 10
5.একটি ত্রিভুজের একটি কোণের পরিমাপ 65° এবং দ্বিতীয়টির পরিমাপ Π /12 ; তৃতীয় কোণটির ষষ্টিক ও বৃত্তীয় মান হিসাব করে লিখি।
সমাধানঃ ত্রিভুজের একটি কোণের পরিমাপ 65° এবং দ্বিতীয় কোণের পরিমাপ $\frac{{\mathrm{\pi}}^{{\mathrm{c}}}}{12} = \frac{180°}{12} = 15°$
∴ তৃতীয় কোণটির ষষ্ঠিক মান = 180°-(65°+15°) = 180° -80° = 100°
∴ তৃতীয় কোণটির বৃত্তীয় মান =$\frac{{\mathrm{\pi}}}{180} \times 100 = \frac{5{\mathrm{\pi}}^{{\mathrm{c}}}}{9}$
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
6. দুটি কোণের সমষ্টি 135° এবং তাদের অন্তরফল π/12 হলে , কোণদুটির ষষ্টিক ও বৃত্তীয় মান নির্ণয় কর ।
সমাধানঃ ধরি , কোণ দুটি হল x এবং y
∴ x+y = 135°—(i)
এবং x-y =$\frac{{\mathrm{\pi}}}{12}$ = 15°[যেহেতু π রেডিয়ান =180°]
∴ x-y = 15° —(ii)
(i) ও (ii) নং সমীকরণ যোগ করে পাই ,
x+y+x-y = 135°+15°
বা, 2x = 150°
বা, x = $\frac{150}{2}$
বা, x = 75°
X এর মান (ii) নং সমীকরণে বসিয়ে পাই ,
75° -y =15°
বা, y = 75°-15°
বা, y = 60°
∴ x ও y এর ষষ্টিক পদ্ধতিতে মান গুলি হল যথাক্রমে 75° এবং 60° ।
∴ X = $\frac{75\pi^c}{180} = \frac{5\pi^c}{12}$
এবং Y = $\frac{60\pi^c}{180} = \frac{\pi^c}{3}$
∴ X ও Y এর বৃত্তীয় মান যথাক্রমে $\frac{5\pi^c}{12}$ এবং $\frac{\pi^c}{3}$
কোণ পরিমাপের ধারণা কষে দেখি ২০|Koshe Dekhi 20 Class 10
7. একটি ত্রিভুজের তিনটি কোণের অনুপাত 2:3:4 হলে , ত্রিভুজটির বৃহত্তম কোণটির বৃত্তীয় মান নির্ণয় কর ।
সমাধানঃ
ধরি , ত্রিভুজের তিনটি কোণ যথাক্রমে 2x , 3x এবং 4x ।
∴ 2x+3x+4x=180° [যেহেতু ত্রিভুজের তিনটি কোণের সমষ্টি 180°]
বা, 9x = 180°
বা, x = 180°/9
বা, x = 20°
∴ বৃহত্তম কোণটি হল 4x = 4✕20° = 80°
বৃহত্তম কোণটির বৃত্তীয় মান = $\frac{80\pi^c}{180} = \frac{4\pi^c}{9}$
8. একটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 28 সেমি. । এই বৃত্তে 5.5 সেমি. দৈর্ঘ্যের বৃত্তচাপ দ্বারা ধৃত কেন্দ্রীয় কোণটির বৃত্তীয় মান হিসাব করে লিখি ।
সমাধানঃ আমরা জানি r দৈর্ঘ্যের ব্যাসার্ধের বৃত্তে , s দৈর্ঘ্যের বৃত্তচাপ বৃত্তের কেন্দ্রে যে কোণ উৎপন্ন করে তার মান ϴহলে , s = rϴ হয় ।
∴ 5.5 = 28ϴ
বা, $\theta = \frac{5.5}{28}$
বা, $\theta = \frac{55}{280}$
বা, $\theta = \frac{11}{56}$
বা, $\theta = \frac{22}{7 \times 16}$
বা, $\theta = \frac{\pi^c}{16}$
∴ কোণটির বৃত্তীয় মান $\frac{\pi^c}{16}$
9. একটি বৃত্তের অসমান দৈর্ঘ্যের দুটি চাপ কেন্দ্রে যে কোণ ধারণ করে আছে তার অনুপাত 5:2 এবং দ্বিতীয় কোণটির ষষ্টিক মান 30° হলে , প্রথম কোণটির ষষ্টিক মান ও বৃত্তীয় মান হিসাব করে লেখ ।
সমাধানঃ ধরি , প্রথম কোণের ষষ্টিক মান ϴ ।
$\therefore \frac{\theta }{30} = \frac{5}{2}$
বা, $\theta = \frac{5 \times 30}{2}$
বা, $\theta = 75$
∴ θ –এর বৃত্তীয় মান
= $\frac{75\pi^c}{180}$ = $\frac{5\pi^c}{12}$
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
10. একটি ঘূর্ণায়মান রশ্মি $- 5\frac{1}{12}\boldsymbol \pi $ কোণ উৎপন্ন করেছে । রশ্মিটি কতবার পূর্ণ আবর্তন করেছে এবং তারপরে আরও কত ডিগ্রী কোণ উৎপন্ন করেছে তা হিসাব করে লিখি ।
সমাধানঃ
$5\frac{1}{12}\pi$
= $-\frac{61}{12} \times 180°$
= – 915°
যেহেতু কোণটি ঋণাত্মক তাই রশ্মিটি ঘড়ির কাঁটার দিকে ঘুরছে । ঘূর্ণায়মান রশ্মি 1 বার পূর্ণ আবর্তনে 360° কোণ উৎপন্ন করে ।
এখন , $\frac{915}{360}$=
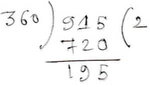
∴ রশ্মিটি ঘড়ির কাঁটার দিকে 2 বার পূর্ণ আবর্তন করেছে এবং তারপর 195° কোণ উৎপন্ন করেছে ।
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন ।
11. ABC একটি সমদ্বিবাহু ত্রিভুজ অঙ্কন করেছি যার সমান বাহুদ্বয়ের অন্তর্ভুক্ত কোণ ∠ABC = 45° ; ∠ABC –এর সমদ্বিখণ্ডক AC বাহুকে D বিন্দুতে ছেদ করেছে । ∠ABD,∠BAD ,∠CBD এবং ∠BCD –এর বৃত্তীয় মান নির্ণয় করি ।
সমাধানঃ
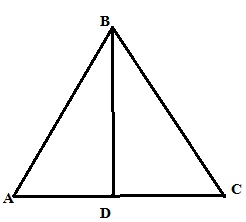
ABC একটি সমদ্বিবাহু ত্রিভুজ অঙ্কন করেছি যার সমান বাহুদ্বয়ের অন্তর্ভুক্ত কোণ ∠ABC = 45° ; ∠ABC –এর সমদ্বিখণ্ডক AC বাহুকে D বিন্দুতে ছেদ করেছে । যেহেতু সমদ্বিবাহু ত্রিভুজের সমান বাহু দ্বয়ের অন্তর্ভুক্ত কোণের সমদ্বিখণ্ডক ,বিপরীত বাহুকে সমকোণে সমদ্বিখন্ডিত করে ।
$\therefore \angle ABD$
= $\frac{\angle ABC}{2}$
= $\frac{45°}{2}$
= $\frac{45}{2} \times \frac{\pi^c}{180}$
= $\frac{\pi^c}{8}$
আবার ,
$\therefore \angle BAD$
= $\frac{180° – \angle ABC}{2}$
= $\frac{180° – 45°}{2}$
= $\frac{135°}{2}$
= $\frac{135}{2} \times \frac{\pi^c}{180}$
= $\frac{3\pi^c}{8}$
যেহেতু BD কোণ ABC –এর সমদ্বিখন্ডক
$\therefore \angle ABD= \angle CBD$
$\therefore \angle CBD= \frac{\pi^c}{8}$
আবার , ABC ত্রিভুজের AB =BC
$\therefore \angle BCD=\angle BAD$
$\therefore \angle {\mathrm{BCD}}= \frac{3{\mathrm{\pi}}^{{\mathrm{c}}}}{8}$
12. ABC সমবাহু ত্রিভুজের BC ভূমিকে E বিন্দু পর্যন্ত এমনভাবে বর্ধিত করলাম যেন CE = BC হয় । A,E যুক্ত করে ACE ত্রিভুজের কোণ গুলির বৃত্তীয়মান নির্ণয় করি ।
সমাধানঃ
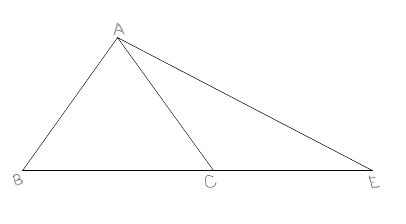
∆ABC একটি সমবাহু ত্রিভুজ ।
∴ AB = BC = CA
আবার , BC =CE
∴ AC =CE
এখন △ACE -এর
∠ACE
=180° – ∠ACB
=180°-60°
=120°
= $\frac{{\mathrm{\pi}}}{180} \times 120$
= $\frac{2{\mathrm{\pi}}}{3}$
যেহেতু, AC = CE
∴ ∠CAE
= ∠CEA
= $\frac{180° – \angle {\mathrm{ACE}}}{2}$
= $\frac{180° – 120°}{2}$
= $\frac{60°}{2}$
= 30°
= $\frac{{\mathrm{\pi}}^{{\mathrm{c}}}}{180} \times 30$
= $\frac{{\mathrm{\pi}}^{{\mathrm{c}}}}{6}$
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
13. কোনো চতুর্ভুজের তিনটি কোণের পরিমাপ যথাক্রমে $\frac{\mathbf \pi }{3},\frac{5\mathbf \pi }{6}$ ও 90° হলে , চতুর্থ কোণটির ষষ্ঠিক ও বৃত্তীয় মান হিসেব করে লিখি ।
সমাধানঃ
চতুর্ভুজটির তিনটি কোণের পরিমাপ যথাক্রমে $\frac{{\mathrm{\pi}}}{3},\frac{5{\mathrm{\pi}}}{6}$ ও 90°
এখন , $90° = \frac{{\mathrm{\pi}}}{180°} \times 90° = \frac{{\mathrm{\pi}}}{2}$
চতুর্থ কোণটির বৃত্তীয় মান
= $2{\mathrm{\pi}} – \left(\frac{{\mathrm{\pi}}}{3} + \frac{5{\mathrm{\pi}}}{3} + \frac{{\mathrm{\pi}}}{6}\right)$ [যেহেতু চতুর্ভুজের চারটি কোণের সমষ্টি 360° = 2π]
= $2{\mathrm{\pi}} – \left(\frac{2{\mathrm{\pi}} + 5{\mathrm{\pi}} + 3{\mathrm{\pi}}}{6}\right)$
=$2{\mathrm{\pi}} – \frac{10{\mathrm{\pi}}}{6}$
= $\frac{12{\mathrm{\pi}} – 10{\mathrm{\pi}}}{6}$
= $\frac{2{\mathrm{\pi}}}{6}$
= $\frac{{\mathrm{\pi}}}{3}$
চতুর্থ কোণটির বৃত্তীয় মান = $\frac{{\mathrm{\pi}}}{3}$
চতুর্থ কোণটির ষষ্ঠিক মান = $\frac{{\mathrm{\pi}}}{3}$ = $\frac{180°}{3}$ = 60°
14. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A)
(A) বহু বিকল্পীয় প্রশ্ন (M.C.Q)
(i) একটি ঘড়ির মিনিটের কাঁটার প্রান্তবিন্দু 1 ঘণ্টায় আবর্তন করে
(a) π/4 রেডিয়ান
(b) π/2 রেডিয়ান
(c ) π রেডিয়ান
(d) 2π রেডিয়ান
Ans: (d) 2π রেডিয়ান
সমাধানঃ 1 ঘণ্টায় ঘড়ির মিনিটের কাঁটার প্রান্তবিন্দু অতিক্রম করে 360° = 2π রেডিয়ান ।
(ii) π/6 রেডিয়ান সমান
(a) 60°
(b) 45°
(c ) 90°
(d) 30°
Ans: (d) 30°
সমাধানঃ $\frac{{\mathrm{\pi}}}{6}$ রেডিয়ান=$\frac{180°}{6} = 30°$
(iii) একটি সুষম ষড়ভুজের প্রতিটি অন্তঃকোণের বৃত্তীয় মান
(a) π/3
(b) 2π/3
(c ) π/6
(d) π/4
Ans: (b) 2π/3
সমাধানঃ একটি সুষম ষড়ভুজের প্রতিটি অন্তঃকোণ
= $\frac{(2{\mathrm{n}} – 4) \times 90°}{{\mathrm{n}}}$
= $\frac{\{ 2(6) – 4\} \times 90}{6}$
=$\frac{720°}{6}$
=120°
(iv) s =rϴ সম্পর্কে ϴ -এর পরিমাপ করা হয়
(a) ষষ্টিক পদ্ধতিতে
(b) বৃত্তীয় পদ্ধতিতে
(c ) ওই দুই পদ্ধতিতে
(d) ওই দুই পদ্ধতির কোনোটিতে নয়
Ans: (b) বৃত্তীয় পদ্ধতিতে
(v) ABCD বৃত্তস্থ চতুর্ভুজের ∠A = 120°হলে , ∠C এর বৃত্তীয় মান
(a) π/3
(b) π/6
(c ) π/2
(d) 2π/3
Ans:
সমাধানঃ যেহেতু বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক , ∴∠A+∠C =180°
∴ ∠C = 180°-∠A
বা, ∠C = 180° -120°
বা, ∠C = 60°
∴ $\angle {\mathrm{C}}$ -এর বৃত্তীয় মান = $\frac{{\mathrm{\pi}}}{180°} \times 60° = \frac{{\mathrm{\pi}}}{3}$
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখিঃ
(i) একটি রশ্মির প্রান্তবিন্দুকে কেন্দ্র করে রশ্মিটির ঘড়ির কাঁটার বিপরীত দিকে ঘোরার জন্য উৎপন্ন কোণটি ধনাত্মক ।
উত্তরঃ বিবৃতিটি সত্য ।
(ii) একটি রশ্মির প্রান্তবিন্দুকে কেন্দ্র করে রশ্মিটির ঘড়ির কাঁটার দিকে দুবার পূর্ণ আবর্তনের জন্য 720° কোণ উৎপন্ন হয় ।
Ans: বিবৃতিটি মিথ্যা ।
সমাধানঃ একটি রশ্মির প্রান্তবিন্দুকে কেন্দ্র করে রশ্মিটির ঘড়ির কাঁটার দিকে দুবার পূর্ণ আবর্তনের জন্য -720° কোণ উৎপন্ন হয় ।
(C ) শূন্যস্থান পূরণ করি ঃ
(i) π রেডিয়ান একটি _________ কোণ ।
উত্তরঃ ধ্রুবক কোণ ।
(ii) ষষ্টিক পদ্ধতিতে 1 রেডিয়ান সমান _______ কোণ (প্রায়)।
উত্তরঃ 1 রেডিয়ান = $\frac{180°}{{\mathrm{\pi}}} = \frac{180°}{\frac{22}{7}} = \frac{180°\times 7}{22} = \frac{630°}{11} = 57°16’22″$
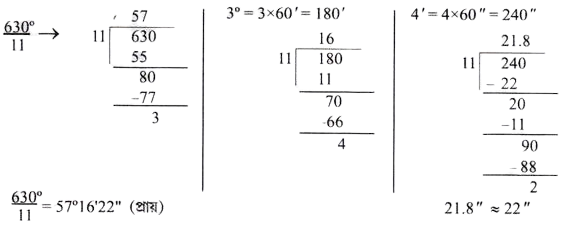
(iii) $\frac{3\mathbf \pi }{8}$ পরিমাপের কোণটির সম্পূরক কোণের বৃত্তীয় মান _____________ ।
উত্তরঃ
$\frac{3{\mathrm{\pi}}}{8}$ পরিমাপের কোণটির সম্পূরক কোণের বৃত্তীয় মান = ${\mathrm{\pi}} – \frac{3{\mathrm{\pi}}}{8}$=$\frac{8{\mathrm{\pi}} – 3{\mathrm{\pi}}}{8}$=$\frac{5{\mathrm{\pi}}}{8}$
15. (i) একটি কোণের ডিগ্রিতে মান D এবং ওই কোণের রেডিয়ানে মান R হলে ,R/D এর মান নির্ণয় করি ।
সমাধানঃ
${\mathrm{\pi}}^{{\mathrm{c}}} = 180°$
$\therefore 1^c = \frac{180}{\pi }$
বা, ${\mathrm{R}}^{{\mathrm{c}}} = \frac{180{\mathrm{R}}}{{\mathrm{\pi}}}$
শর্তানুসারে,
$D = \frac{180R}{\pi }$
বা, $\frac{{\mathrm{\pi}}}{180} = \frac{{\mathrm{R}}}{{\mathrm{D}}}$
$\therefore \frac{{\mathrm{R}}}{{\mathrm{D}}} = \frac{{\mathrm{\pi}}}{180}$
(ii) 63°35’15” পরিমাপের কোণটির পূরক কোণের মান লিখি ।
সমাধানঃ 90° = 89°60′ = 89°59’60”
∴ 63°35’15” পরিমাপের কোণটির পূরক কোণের মান
= 89°59’60”-63°35’15”=26°24’45”
(iii) একটি ত্রিভুজের দুটি কোণের পরিমাপ 65°56’55” এবং 64°3’5” হলে, তৃতীয় কোণটির বৃত্তীয় মান নির্ণয় করি ।
সমাধানঃ তৃতীয় কোণটির ষষ্টিক মান
= 180° -(65°56’55”+64°3’5”)
= 180° -130°
= 50°
তৃতীয় কোণটির বৃত্তীয় মান = $50 \times \frac{{\mathrm{\pi}}^{{\mathrm{c}}}}{100} = \frac{{\mathrm{\pi}}^{{\mathrm{c}}}}{2}$
(iv) একটি বৃত্তে 220 সেমি. দৈর্ঘ্যের বৃত্তচাপ কেন্দ্রে 63°পরিমাপের কোণ উৎপন্ন করলে, বৃত্তের ব্যাসার্ধের দৈর্ঘ্য নির্ণয় করি।
সমাধানঃ
$63 = 63° \times \frac{\pi^c}{180} = \frac{21\pi^c}{60}$
আমরা জানি, s =rθ [ s= বৃত্তচাপের দৈর্ঘ , r = বৃত্তের ব্যাসার্ধ , θ =কেন্দ্রে উৎপন্ন কোণের বৃত্তীয় মান]
$\therefore 220 = r \times \frac{21\pi }{60}$
বা, ${\mathrm{r}} = \frac{220 \times 60}{21{\mathrm{\pi}}}$
বা, ${\mathrm{r}} = \frac{220 \times 60}{21 \times \frac{22}{7}}$
বা, ${\mathrm{r}} = \frac{220 \times 60}{3 \times 22}$
বা, ${\mathrm{r}} = 200$
∴ বৃত্তের ব্যাসার্ধ 200 সেমি. ।
(v) একটি ঘড়ির ঘণ্টার কাঁটার প্রান্তবিন্দু 1 ঘণ্টা আবর্তনে যে পরিমাণ কোণ উৎপন্ন করে তার বৃত্তীয় মান লিখি ।
সমাধানঃ একটি ঘড়ির ঘণ্টার কাঁটা 12 ঘণ্টায় কেন্দ্রে 360° বা 2π রেডিয়ান কোণ উৎপন্ন করে ।
∴ 1 ঘন্টায় কেন্দ্রে উৎপন্ন করা কোণের পরিমাপ = $\frac{2\pi }{12} = \frac{\pi }{6}$
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
খুবই্ ভালো কাজ। চালিয়ে যান, অনেক উন্নতি হবে আপনার,,,,,,,,,,,
Thanks