Ganit Prabha Class 8 Koshe Dekhi 7.1|বিপ্রতীপ কোণের ধারণা কষে দেখি ৭.১|গণিতপ্রভা ক্লাস ৮ কষে দেখি ৭.১ সমাধান|গণিতপ্রভা অষ্টম শ্রেণি কষে দেখি ৭.১ সমাধান|WBBSE Class 8 Chapter 7 Exercise 7.1 Solution.
গণিতপ্রভা অষ্টম শ্রেণির বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
Ganit Prabha Class 8 Koshe Dekhi 7.1|বিপ্রতীপ কোণের ধারণা কষে দেখি ৭.১|গণিতপ্রভা ক্লাস ৮ কষে দেখি ৭.১ সমাধান|গণিতপ্রভা অষ্টম শ্রেণি কষে দেখি ৭.১ সমাধান|WBBSE Class 8 Chapter 7 Exercise 7.1 Solution.
1.দুটি সরলরেখা PQ ও RS পরস্পরকে O বিন্দুতে ছেদ করলে বিপ্রতীপ কোণগুলি তৈরি হয় তাদের আঁকি ও নাম লিখি ।
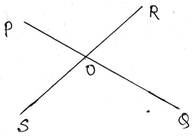
সমাধানঃ দুটি সরলরেখা PQ ও RS পরস্পরকে O বিন্দুতে ছেদ করলে যে বিপ্রতীপ কোণগুলি তৈরি হয় সেগুলি হল ∠POS ও ∠ROQ এবং ∠POR ও ∠SOQ ।
2. ছবি দেখি ও কোণগুলির মান লেখার চেষ্টা করি ঃ
(a) ∠1=350 , ∠2 = ? , ∠ 3 = ? , ∠4 = ?
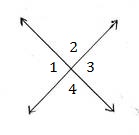
সমাধানঃ
∠1=বিপ্রতীপ ∠3 এবং ∠2=বিপ্রতীপ ∠4
∵ ∠1=350 , ∴ ∠3=350
আবার , ∠1+ ∠2=1800
∴ ∠2 =1800 – ∠1
বা, ∠2 = 1800 -350
বা, ∠2=1450
∴ ∠4=1450
(b) ∠TOS=200 , ∠ROQ=600 , ∠POT= ? , ∠ROP= ? ∠QOS= ?
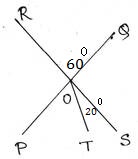
সমাধানঃ ∠ROQ= বিপ্রতীপ ∠POS এবং ∠ROP= বিপ্রতীপ ∠QOS
∠ROQ=600
সুতরাং , ∠POS=600
বা, ∠POT+ ∠TOS=600
বা, ∠POT=600 – ∠TOS
বা, ∠POT=600 – 200
∴ ∠POT=400
∠ROP+ ∠ROQ=1800
বা, ∠ROP=1800 – ∠ROQ
বা, ∠ROP=1800 – 600
∴ ∠ROP=1200
∴ ∠QOS=1200 [∵∠ROP=বিপ্রতীপ ∠QOS]
Ganit Prabha Class 8 Koshe Dekhi 7.1|বিপ্রতীপ কোণের ধারণা কষে দেখি ৭.১
3. তীর্থ PQ ও XY দুটি সরলরেখা আঁকল যারা পরস্পরকে O বিন্দু ছেদ করেছে । আমি চাঁদার সাহায্যে বিপ্রতীপ কোনগুলি মেপে দেখি ।
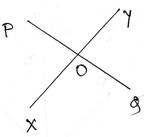
সমাধানঃ PQ ও XY দুটি সরলরেখা পরস্পরকে O বিন্দুতে ছেদ করার ফলে যে দুই জোড়া বিপ্রতীপ কোণ উৎপন্ন হয় সেগুলি হল ∠POX ও ∠YOQ এবং ∠POY ও ∠XOQ
চাঁদার সাহায্যে মেপে দেখলাম , ∠POX= বিপ্রতীপ ∠YOQ=300 এবং ∠XOQ= বিপ্রতীপ ∠POY=1200
[Note: কোণগুলির পরিমাপ আলাদাও হতে পারে]
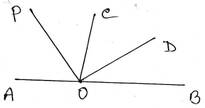
4. পাশের ছবি দেখি ও নীচের প্রশ্নের উত্তর খোঁজার চেষ্টা করি ঃ
(i)দুটি কোণের নাম লিখি যারা পরস্পর পূরক কোণ ।
(ii)দুটি কোণের নাম লিখি যারা পরস্পর সম্পূরক কোণ ।
(iii)দুটি কোণের নাম লিখি যারা পরস্পর বিপ্রতীপ কোণ ।
সমাধানঃ
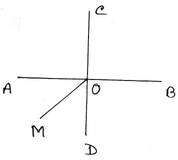
(i)∠AOM ও ∠DOM কোণ দুটি পরস্পর পূরক কোণ ।
(ii)∠AOC ও ∠BOC কোণ দুটি পরস্পর সম্পূরক কোণ ।
[এছাড়াও ,∠BOC ও ∠DOB কোণ দুটি পরস্পর সম্পূরক কোণ]
(iii)∠AOD ও ∠COB কোণ দুটি পরস্পর বিপ্রতীপ কোণ ।
[এছাড়াও ,∠AOC ও ∠DOB কোণ দুটি পরস্পর সম্পূরক কোণ ]
5. দুটি সরলরেখা কোনো বিন্দুতে ছেদ করলে বিপ্রতীপ কোণগুলির পরিমাপ সমান হবে যুক্তি দিয়ে প্রমান করি ।
AB ও CD সরলরেখা দুটি পরস্পরকে O বিন্দুতে ছেদ করে । এর ফলে দুজোড়া বিপ্রতীপ কোণ ∠AOD, ∠BOC ও ∠AOC, ∠BOD তৈরি হয়েছে
প্রমাণ করতে হবে যে, বিপ্রতীপ কোণ জোড়া দুটি সমান অর্থাৎ ∠AOD=∠BOC ও ∠AOC=∠BOD
প্রমাণঃ
∠AOC+∠AOD=1800 [∵ CD সরলরেখার উপর OA দণ্ডায়মান]
∠AOC+∠BOC=1800 [∵ AB সরলরেখার উপর OC দণ্ডায়মান]
∠AOC+∠AOD=∠AOC+∠BOC
∴ ∠AOD=∠BOC
আবার,
∠BOC+∠BOD=1800 [∴CD সরলরেখার উপর OB দণ্ডায়মান]
∠AOC+∠BOC=1800[∵AB সরলরেখার উপর OC দণ্ডায়মান]
∠BOC+∠BOD=∠AOC+∠BOC
∴ ∠BOD=∠AOC
সুতরাং, ∠AOD=∠BOC এবং ∠BOD=∠AOC [প্রমানিত]
6. ∠BOD, ∠BOC এবং ∠AOC এর পরিমাপ লিখি ।
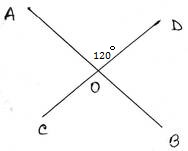
সমাধানঃ ∠BOC = বিপ্রতীপ ∠AOD = 1200
∠AOC + ∠BOC = 1800 [∵AB সরলরেখার উপর OC দণ্ডায়মান]
∴ ∠AOC = 1800 – 1200= 600
সুতরাং , ∠BOD = 600, ∠BOC = 1200 এবং ∠AOC = 600
7. ∠POR ও ∠QOS এর সমষ্টি 1100 ; ∠POS, ∠QOS, ∠QOR ও ∠POR এর পরিমাপ লিখি ।
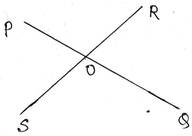
সমাধানঃ ∠POR = বিপ্রতীপ ∠QOS
আবার, ∠POR+∠QOS=1100
বা, ∠POR+∠POR=1100
বা, 2∠POR=1100
বা, ∠POR= 1100/2
∴ ∠POR=550
∴ ∠QOS=550
∠POR+∠POS=1800 [ ∵RS সরলরেখার উপর OP দণ্ডায়মান]
∴∠POS=1800-550 = 1250
∠QOR = বিপ্রতীপ ∠POS =1250
সুতরাং, ∠POS=1250, ∠QOS=550, ∠QOR=1250 ও ∠POR=550
8. OP, OQ, OR এবং OS সমবিন্দু । OP এবং OR একই সরল রেখায় অবস্থিত । P ও R বিন্দু O বিন্দুর বিপরীত পাশে অবস্থিত । ∠POQ= ∠ROS এবং ∠POS= ∠QOR । যদি ∠POQ=500 হয় তবে ∠QOR, ∠ROS এবং ∠POS এর পরিমাপ লিখি ।
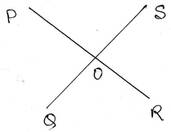
সমাধানঃ ∠POQ= ∠ROS এবং ∠POQ=500
∴∠ROS=500
OP এবং OR একই সরলরেখায় অবস্থিত।
∴ ∠POS+∠ROS=1800
বা, ∠POS+500=1800
বা, ∠POS=1800-500
∴ ∠POS=1300
আবার, ∠POS=∠QOR
∴ ∠QOR= 1300
সুতরাং ∠QOR= 1300, ∠ROS= 500, এবং ∠POS=1300
Ganit Prabha Class 8 Koshe Dekhi 7.1|বিপ্রতীপ কোণের ধারণা কষে দেখি ৭.১
গণিতপ্রভা অষ্টম শ্রেণির বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
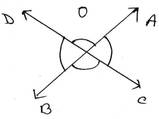
9. চারটি রশ্মি একটি বিন্দুতে এমনভাবে মিলিত হয় যে বিপরীত দিকের কোণগুলি সমান । প্রমান করি যে ওই চারটি রশ্মি দ্বারা দুটি সরলরেখা তৈরি হয় ।
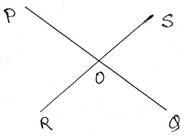
চারটি রশ্মি PO, RO, QO এবং SO, O বিন্দুতে এমনভাবে মিলিত হয়েছে যে বিপরীত দিকের কোণগুলি সমান অর্থাৎ ∠POS= ∠ROQ এবং ∠POR= ∠SOQ
প্রমাণ করতে হবে যে , PO, RO, QO এবং SO দিয়ে দুটি সরলরেখা তৈরি হয় ।
প্রমাণঃ চারটি রশ্মি PO, RO, QO এবং SO , O বিন্দুতে মিলিত হয়েছে ।
∴ ∠POS+∠POR+∠ROQ+∠SOQ = 3600
বা, ∠ROQ+∠SOQ+∠ROQ+∠SOQ = 3600 [∵∠POS=∠ROQ এবং ∠POR=∠SOQ]
বা, 2(∠ROQ+∠SOQ)= 3600
∴ ∠ROQ+∠SOQ = 1800
∴ ∠ROQ ও ∠SOQ সন্নিহিত কোণ দুটির সমষ্টি 1800
সুতরাং, R,S বিন্দুদ্বয় একই সরল রেখায় অবস্থিত ।
এখন , ∠POS+∠SOQ
=∠ROQ+∠SOQ [∵∠POS=∠ROQ]
=1800
∴ ∠POS ও ∠SOQ সন্নিহিত কোণ দুটির সমষ্টি 1800
সুতরাং, P,Q বিন্দুদ্বয় একই সরলরেখায় অবস্থিত ।
∴ PO, RO, QO এবং SO, O বিন্দুতে মিলিত হওয়ার ফলে PQ ও RS দুটি সরল রেখা তৈরি হল ।
সুতরাং, PO, RO, QO এবং SO দিয়ে দুটি সরলরেখা তৈরি হয় । [প্রমানিত]
10. একটি কোণের অন্তঃসমদ্বিখণ্ডিত ও বহিঃসমদ্বিখণ্ডিত পরস্পর লম্বভাবে অবস্থিত প্রমাণ করি ।
একটি কোণ ∠BOC এর অন্তঃসমদ্বিখণ্ডিত OD এবং বহিঃসমদ্বিখণ্ডিত OP
প্রমাণ করতে হবে যে, OD ও OP পরস্পর লম্ব ভাবে অবস্থিত
প্রমাণঃ ∠BOC –এর বহিকোণ ∠AOC
সুতরাং , ∠BOC + ∠AOC = 1800 —-(i)
∠BOC –এর অন্তঃসমদ্বিখন্ডক OD
∴ ∠BOC = 2∠COD —-(ii)
আবার, ∠BOC এর বহিঃকোণ, ∠AOC এর অন্তঃসমদ্বিখণ্ডক OP
∴ ∠AOC = 2∠COP —(iii)
(i) নং থেকে পাই ,
∠BOC+∠AOC= 1800
বা, 2∠COD+2∠COP = 1800
বা, 2(∠COD+∠COP) = 1800
∴ ∠COD+∠COP = 900
সুতরাং, OD ও OP পরস্পর লম্ব ।
Ganit Prabha Class 8 Koshe Dekhi 7.1|বিপ্রতীপ কোণের ধারণা কষে দেখি ৭.১
11. দুটি সরলরেখা পরস্পর ছেদ করলে যা চারটি কোণ উৎপন্ন হয় তাদের সমষ্টি চার সমকোণের সমান-প্রমাণ করি ।
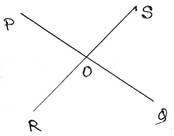
PQ ও RS সরলেরখা দুটি পরস্পরকে O বিন্দুতে ছেদ করেছে । এর ফলে ∠POR, ∠ROQ, ∠SOQ, ও ∠POS চারটি কোণ তৈরি হয়েছে ।
প্রমাণ করতে হবে যে , ∠POR +∠ROQ +∠SOQ +∠POS = 4 সমকোণ
প্রমাণঃ PQ সরলরেখার উপর OR রশ্মি দণ্ডায়মান
∴ ∠POR+∠ROQ=1800 —(i)
আবার, PQ সরলরেখার উপর OS রশ্মি দণ্ডায়মান
∴ ∠POS+∠SOQ=1800 —-(ii)
(i) নং ও (ii) নং সমীকরণ যোগ করে পাই ,
∠POR+∠ROQ+∠POS+∠SOQ =1800+1800
বা, ∠POR+∠ROQ+∠POS+∠SOQ =3600
∴∠POR+∠ROQ+∠POS+∠SOQ =4 সমকোণ [প্রমাণিত]
12. PQC ত্রিভুজের ∠PQR =∠PQR; QR বাহু কে উভয়দিকে বর্ধিত করলে যে দুটি বহিঃকোণ উৎপন্ন হয় তাদের মান সমান-প্রমাণ করি ।
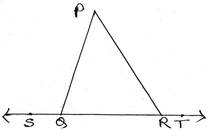
PQR ত্রিভুজের ∠PQR =∠PQR , QR বাহুকে উভয়দিকে যথাক্রমে S ও T পর্যন্ত বর্ধিত করার ফলে যথাক্রমে দুটি বহিঃকোণ ∠PQS এবং ∠PRT তৈরি হল ।
প্রমাণ করতে হবে যে , ∠PQS =∠PRT
প্রমাণঃ SR সরলরেখার উপর QP রশ্মি দণ্ডায়মান
∴ ∠PQS+∠PQR= 1800 —(i)
আবার, QT সরলরেখার উপর RP রশ্মি দণ্ডায়মান
∴ ∠PRT+∠PRQ= 1800—(ii)
(i) নং ও (ii) নং সমীকরণ থেকে পাই ,
∠PQS+∠PQR =∠PRT+∠PRQ
বা, ∠PQS+∠PRQ =∠PRT+∠PRQ [∵∠PQR=∠PQR]
∴ ∠PQS=∠PRT [প্রমাণিত]
Ganit Prabha Class 8 Koshe Dekhi 7.1|বিপ্রতীপ কোণের ধারণা কষে দেখি ৭.১
13. দুটি সরলরেখা পরস্পরকে একটি বিন্দুতে ছেদ করায় যে চারটি কোণ উৎপন্ন হয় তাদের সমদ্বিখণ্ডকগুলি পরস্পর দুটি লম্ব সরলরেখা- প্রমাণ করি ।
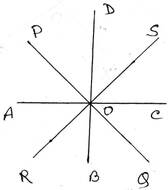
PQ ও RS সরলরেখা পরস্পরকে O বিন্দুতে ছেদ চারটি কোণ∠POR, ∠ROQ, ∠SOQ ও∠POS উৎপন্ন হয়েছে । AO, BO, CO ও DO যথাক্রমে চারটি কোণগুলির সমদ্বিখণ্ডক ।
প্রমাণ করতে হবে যে , সমদ্বিখণ্ডকগুলি পরস্পর দুটি লম্ব সরলরেখা অর্থাৎ, AO, OC এবং BO, OD একই সরলরেখায় আছে এবং AC ⊥ BD
প্রমাণঃ
∠POS= বিপ্রতীপ ∠ROQ [প্রদত্ত]
এবং ∠POR= বিপ্রতীপ ∠SOQ [প্রদত্ত]
AO, ∠POR এর সমদ্বিখণ্ডক, ∴ ∠AOP=∠AOR= ½ ∠POR
BO, ∠QOR এর সমদ্বিখণ্ডক , ∴ ∠BOR=∠BOQ= ½ ∠ROQ
CO, ∠SOQ এর সমদ্বিখণ্ডক , ∴ ∠COS=∠COQ= ½ ∠SOQ
DO, ∠POR এর সমদ্বিখণ্ডক , ∴ ∠DOP=∠DOS= ½ ∠POS
এখন , ∠AOD+∠AOB
=∠DOP+∠AOP+∠AOR+∠ROB
= ½ ∠POS+∠POR+ ½ ∠ROQ [∵∠POS= বিপ্রতীপ ∠ROQ]
= ½ ∠ROQ+∠POR+ ½ ∠ROQ
= ∠ROQ+∠POR
= 1800 [∵PQ সরলরেখার উপর OR দণ্ডায়মান]
∠AOD ও ∠AOB সন্নিহিত কোণ দুটির সমষ্টি 1800
∴ OB ও OD একই সরলরেখায় অবস্থিত
অনুরূপভাবে প্রমাণ করা যায় যে,
AO ও OC একই সরলরেখায় অবস্থিত
∠AOD =∠AOP+∠POD
= ½ ∠ROP + ½ ∠POS
= ½ (∠ROP +∠POS)
= ½ x 1800 [∵ RS সরলরেখার উপর OP দণ্ডায়মান]
= 900
∴ AC ও BD সরলরেখা দুটি পরস্পর লম্ব ।
∴ AC ⊥ BD [প্রমাণিত ]
Ganit Prabha Class 8 Koshe Dekhi 7.1|বিপ্রতীপ কোণের ধারণা কষে দেখি ৭.১
গণিতপ্রভা অষ্টম শ্রেণির বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।