Madhyamik 2018 Math Question Solution.মাধ্যমিক ২০১৮ গণিত সমাধান । WBBSE Madhyamik 2018 Question Solution.
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
1. নিম্নলিখিত প্রশ্নগুলির প্রতিটি ক্ষেত্রে সঠিক উত্তরটি নির্বাচন করঃ
(i) বার্ষিক 10% সরল সুদের হারে a টাকার b মাসের সুদঃ
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
(ii) যদি x ∝ y হয় ,তাহলে
(a) x2 ∝ y3
(b) x3 ∝ y2
(c ) x ∝ y2
(d) x2 ∝ y2
Ans: (d) x2 ∝ y2
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
(iii) ABCD বৃত্তস্থ চতুর্ভুজের ∠A =100° হলে ∠C এর মান-
(a) 50°
(b) 200°
(c ) 80°
(d) 180°
Ans: (c ) 80°
সমাধানঃ ABCD বৃত্তস্থ চতুর্ভুজের ∠A+∠C = 180° [ যেহেতু বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক ]
∴ ∠C = 180°-∠A
বা, ∠C = 180°-100°
বা, ∠C = 80°
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
(iv) 7π/12 এর ষষ্টিক পদ্ধতিতে মান হলঃ
(a) 115°
(b) 150°
(c) 135°
(d) 105°
Ans: (d) 105°
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
(v) একটি ঘনকের একটি বাহুর দৈর্ঘ্য a একক এবং কর্ণের দৈর্ঘ্য d একক হলে a এবং d –এর সম্পর্ক হবেঃ
(a) √2a = d
(b) √3a = d
(c ) a =√3d
(d) a =√2 d
Ans: (b) √3a = d
সমাধানঃ
একটি ঘনকের একটি বাহুর দৈর্ঘ্য a একক এবং কর্ণের দৈর্ঘ্য d একক হলে d = a√3
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
(vi) 6,7,x,y,16 সংখ্যা গুলির গড় 9 হলেঃ
(a) x+y = 21
(b) x+y=17
(c ) x-y=21
(d) x-y=19
Ans: (b) x+y=17
সমাধানঃ 6,7,x,8,y,16 সংখ্যাগুলির গড় 9
বা, x+y+37 = 54
বা, x+y = 17
বা, x+y = 17
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
2. শূন্যস্থান পূরণ কর (যে কোনো 5 টি ):
(i) বার্ষিক r% হার সরল সুদের হারে কোনো মূলধনের n বছরের সুদ pnr /25 টাকা হলে মূলধনের পরিমাণ __________ টাকা হবে ।
Ans:
সমাধানঃ ধরি , মূলধনের পরিমাণ x টাকা
∴ মূলধনের পরিমাণ 4P টাকা ।
(ii) (a-2)x2 +3k+5=0 সমীকরণটিতে a- এর মান _______ এর জন্য দ্বিঘাত সমীকরণ হবে না ।
Ans: 2
সমাধানঃ এক্ষেত্রে a =2 হলে দ্বিঘাত সমীকরণটির x2 এর সহগ শূন্য হয় ।
(iii) ABCD একটি বৃত্তস্থ সামান্তরিক হলে ∠A এর মান হবে ________ ।
Ans: 90°
সমাধানঃ যেহেতু বৃত্তস্থ সামন্তরিক একটি আয়তক্ষেত্র ।
(iv) tan35° tan55° =sinϴ হলে , ϴ এর সর্বনিম্ন মান ________ হবে ।
Ans: 90°
সমাধানঃ
tan35° tan55° =sinϴ
বা, tan35° tan(90°-35°) = sinϴ
বা, tan35° cot35° = sinϴ
বা, sinϴ = 1 =sin90°
বা, ϴ =90°
(v) একমুখ কাটা একটি পেনসিলের আকার চোঙ ও ________ এর সমন্বয় ।
Ans: শঙ্কু।
(vi) মধ্যগামীতার মাপকগুলি হল গড় , মধ্যমা ও ________ ।
Ans: সংখ্যাগুরুমান।
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।
মাধ্যমিকের সকল বিষয়ের বিগত বছরের প্রশ্ন উত্তর (Click Here)
3. সত্য ও মিথ্যা লেখো ঃ
(i) নির্দিষ্ট আসলের উপর সমান হারে সুদ হলে 2 বছরের সরল সুদ , চক্রবৃদ্ধি সুদের তুলনায় বেশি ।
উত্তরঃ মিথ্যা ।
(ii) x3y ,x2y2 এবং xy3 ক্রমিক সমানুপাতী
উত্তরঃ সত্য ।
বা, x3y : x2y2 :: x2y2 : xy3
∴ x3y ,x2y2 এবং xy3 ক্রমিক সমানুপাতী ।
(iii) অর্ধ বৃত্ততাংসস্থ অপেক্ষা ক্ষুদ্রতর বৃত্তাংসস্থ কোণ স্থুলকোণ ।
উত্তরঃ মিথ্যা ।
(iv) sec227° -cot263° -এর সরলতম মান 1.
উত্তরঃ সত্য ।
সমাধানঃ
sec227° -cot263°
= sec227° – cot2 (90°-27°)
= sec2 27° -tan227°
= 1
(v) একটি গোলকের ব্যাসার্ধ দ্বিগুন হলে গোলকটির আয়তন প্রথম গোলকের আয়তনের দ্বিগুন হবে ।
Ans: মিথ্যা ।
সমাধানঃ ধরি , গোলকের ব্যাসার্ধ r একক ।
গোলকের ব্যাসার্ধ দ্বিগুন হলে গোলকের পরিবর্তিত ব্যাসার্ধ হবে 2r একক ।
∴ এখন গোলকের আয়তন
= 8✕ প্রথম গোলকের আয়তন
∴ পরিবর্তিত গোলকের আয়তন ,প্রথম গোলকের আয়তনের 8 গুন হবে ।
(vi)
| স্কোর | 1 | 2 | 3 | 4 | 5 |
| শিক্ষার্থী সংখ্যা | 3 | 6 | 4 | 7 | 5 |
বিভাজনটির সংখ্যাগুরু মান হল 3.
উত্তরঃ মিথ্যা ।
সমাধানঃ এক্ষেত্রে স্কোর 4 এর পরিসংখ্যা 7 যা সবথেকে বেশি ।
∴ সংখ্যাগুরু মান 4
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ
সমাধানঃ ধরি , ওই ব্যাক্তির মূলধন x টাকা ।
∴ x টাকার 1 বছরের 4% হারে সুদ
∴ ওই ব্যাক্তির মূলধন 2400 টাকা ।
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
(ii) A এবং B যথাক্রমে 15000 টাকা ও 45000 টাকা দিয়ে একটি ব্যাবসা শুরু করল । 6 মাস পরে B লভ্যাংশ হিসেবে 3030 টাকা পেল । A-এর লভ্যাংশ কত ?
সমাধানঃ ধরি , A এর লভ্যাংশ x টাকা ।
∴ A এর মূলধন : B এর মূলধন = A এর লভ্যাংশ : B এর লভ্যাংশ
বা, 15000:45000 = x:3030
বা, 1:3 = x:3030
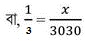
বা, 3x = 3030
বা, x = 3030/3
বা, x = 1010
∴ A এর লভ্যাংশ 1010 টাকা ।
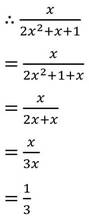
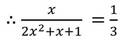
(iv) কোনো দ্বিঘাত সমীকরণের বীজদ্বয় 2 ও -3 হলে সমীকরণটি লেখ ।
সমাধানঃ নির্ণেয় সমীকরণটি হবে
= X2 – (বীজদ্বয়ের যোগফল )x + ( বীজদ্বয়ের গুনফল ) = 0
বা, X2 –{2+(-3)}x +(2)(-3) =0
বা, x2 –(-x) -6 = 0
বা, x2 +x -6=0
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
(v) ABC –এর BC বাহুর সমান্তরাল সরলরেখা AB ও AC কে যথাক্রমে P ও Q বিন্দুতে ছেদ করে । যদি AP = 4 সেমি. , QC = 9 সেমি. এবং PB =AQ হয় তাহলে PB এর দৈর্ঘ্য নির্ণয় কর ।
সমাধানঃ
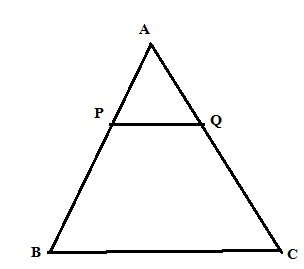
ABC ত্রিভুজের BC বাহুর সমান্তরাল সরলরেখা AB ও AC কে জথাক্রমে P ও Q বিন্দুতে ছেদ করে । ধরি , PB =AQ = x সেমি.
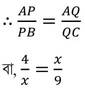
বা, x2 = 36
বা, x2 = (6)2
বা, x = 6
∴ PB = 6 সেমি.
(vi) O কেন্দ্রীয় বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি. । এবং O বিন্দু থেকে 13 সেমি দূরত্বে P একটি বিন্দু । PQ ও PR বৃত্তের দুটি স্পর্শক হলে PQOR চতুর্ভুজের ক্ষেত্রফল কত ?
সমাধানঃ
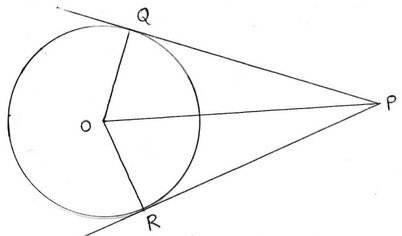
∆OPR ত্রিভুজে OR = 5 সেমি. ( বৃত্তের ব্যাসার্ধ ) , OP = 13 সেমি.
যেহেতু OR স্পর্শবিন্দুগামী ব্যাসার্ধ ∴ OR ⊥ PR
∴ সমকোণী ত্রিভুজ ∆OPR থেকে পাই ,
OR2+PR2=OP2
বা, (5)2+PR2=(13)2
বা, PR2 = 169-25
বা, PR2 = 144
বা , PR2= (12)2
বা, PR = 12
যেহেতু , PR এবং PQ দুটি স্পর্শক এবং P বহিঃস্থ বিন্দু
∴ PR = PQ = 12 সেমি.
PQOR চতুর্ভুজের ক্ষেত্রফল = ত্রিভুজ ∆POR এর ক্ষেত্রফল + ত্রিভুজ ∆POQ এর ক্ষেত্রফল
= ½ ✕ 12 ✕ 5 + ½ ✕ 12 ✕ 5 বর্গ সেমি. [ ∵সমকোণী ত্রিভুজের ক্ষেত্রফল =½✕ ভুমি ✕ উচ্চতা ]
= (30+30) বর্গ সেমি.
= (30+30) বর্গ সেমি.
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
(vii) O কেন্দ্রীয় বৃত্তে AB ও CD জ্যা দুটি কেন্দ্র থেকে সমদূরবর্তী AOB =60° এবং CD=6 সেমি. হলে , বৃত্তের ব্যাসার্ধের দৈর্ঘ্য কত ?
সমাধানঃ O কেন্দ্রীয় বৃত্তে AB ও CD জ্যা দুটি কেন্দ্র থেকে সমদূরবর্তী । ∴ AB = CD = 6 সেমি. ।
ত্রিভুজ AOB এর ,
∠AOB = 60°
আবার OA = OB [ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠OAB =∠OBA = (180°-∠AOB)/2 = (180°-60°)/2 = 60°
সুতরাং AOB সমবাহু ত্রিভুজ ।
∴ OA=OB=AB = 6 সেমি.
∴ বৃত্তের ব্যাসার্ধ 6 সেমি. ।
(viii) tanϴ+ cotϴ=2 হলে , tan7ϴ+cot7ϴ =?
সমাধানঃ
tanϴ+ cotϴ =2
বা, tan2ϴ +1 = 2tanϴ
বা, tan2ϴ -2tanϴ +1 =0
বা, (tanϴ-1) 2 =1
বা, (tanϴ-1) =0
বা, tanϴ =1
∴ tan7ϴ+cot7ϴ = (1)7+(1)7 = 1+1=2
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
(ix) একটি স্তম্ভের ছায়ার দৈর্ঘ্য এবং স্তম্ভের দৈর্ঘ্যের অনুপাত √3 : 1 হলে , সূর্যের উন্নতি কোণ নির্ণয় কর ।
সমাধানঃ
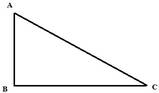
ধরাযাক , পোস্টটির উচ্চতা AB এবং পোস্টের ছায়ার দৈর্ঘ্য BC এবং সূর্যের উন্নতি কোণ ϴ
বা, tan ϴ = tan30°
বা, ϴ = 30°
(x) একটি লম্ব বৃত্তাকার চোঙের আয়তন সমান ও তাদের উচ্চতার অনুপাত 1:2 হলে , চোঙ দুটির ব্যাসার্ধের দৈর্ঘ্যের অনুপাত নির্ণয় কর ।
সমাধানঃ ধরি , দুটি লম্ব বৃত্তাকার চোঙের উচ্চতা যথাক্রমে h1 একক এবং h2 একক এবং ব্যাসার্ধের দৈর্ঘ্য r1 একক এবং r2 একক ।
∴ h1 : h2 = 1:2
যেহেতু লম্ববৃত্তাকার চোঙদুটির আয়তন সমান
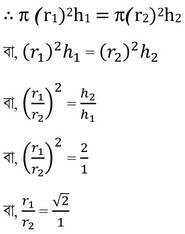
∴ চোঙ দুটির ব্যাসার্ধের অনুপাত √2 : 1 ।
(xi) একটি নিরেট অর্ধ গোলকের আয়তন 144π ঘন সেমি. হলে , গোলকটির ব্যাসের দৈর্ঘ্য কত ?
সমাধানঃ ধরি , অর্ধ গোলকটির ব্যাসার্ধের দৈর্ঘ্য r সেমি. ।
বা, r3 = 216
বা, r3 = (6)3
∴ r = 6
∴ 2r = 12
∴ অর্ধ গোলকের ব্যাসের দৈর্ঘ্য 12 সেমি. ।
(xii) একটি পরিসংখ্যা বিভাজনের গড় 8.1 , ∑fixi = 132+5k এবং ∑fi = 20 হলে , K এর মান কত ?
সমাধানঃ
একটি পরিসংখ্যা বিভাজনের গড় 8.1
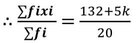
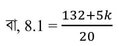
বা, 162 = 132+5k
বা, 5k = 162-132
বা, 5k = 30
বা, k = 30/5
বা, k = 6
∴ k এর মান 6
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।
5.
(a) আমিনুর একটি ব্যাঙ্ক থেকে 64000 টাকা ধার নিয়েছে । যদি ব্যাঙ্কের সুদের হার প্রতি বছরে প্রতি টাকায় 2.5 পয়সা হয় , তবে ওই টাকার 2 বছরের চক্রবৃদ্ধি সুদ কত হবে ?
সমাধানঃ আসল (P) = 64000 টাকা ।
সময় (n) = 2 বছর ।
∴ চক্রবৃদ্ধি সুদ = 67240 টাকা – 64000 টাকা = 3240 টাকা ।
উত্তরঃ 2 বছর পর চক্রবৃদ্ধি সুদ হবে 3240 টাকা ।
(b) A ,B ও C 6000 টাকা ,8000 টাকা ও 9000 টাকা মূলধন নিয়ে একত্রে ব্যাবসা আরম্ভ করল । কয়েক মাস পর A আরও 2000 টাকা ব্যাবসায় লগ্নী করল । বছরের শেষে মোট 30000 টাকা লাভ হল এবং C 10800 টাকা লভ্যাংশ পেল । A কখন আরও 3000 টাকা লগ্নী করল ?
সমাধানঃ ধরি , ব্যাবসা শুরু করার x মাস পরে A আরও 3000 টাকা লগ্নী করে ।
∴ A ,B ও C এর মূলধনের অনুপাত
= {(6000✕x)+(6000+3000)(12-x)}: (8000´12) : (9000´12)
= 6000x-9000x+108000 : 96000 : 108000
= 108000-3000x : 96000 : 108000
= 1000(108-3x) : 96000 : 108000
= (108-3x) : 96 :108
= (36-x) : 32 :36
প্রশ্নানুসারে ,
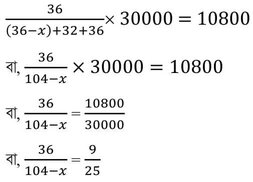
বা, 9(104-x) = 900
বা, 936 -9x =900
বা, -9x = 900-936
বা, -9x = -36
বা, x = -36/-9
বা, x = 4
∴ ব্যাবসা শুরুর 4 মাস পর A ব্যাবসায় 3000 টাকা লগ্নী করে ।
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
6.
(a) সমাধান করঃ
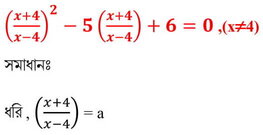
∴ প্রদত্ত দ্বিঘাত সমীকরণটি হল ,
a2 -5a+6 =0
বা, a2 –(3+2)a+6=0
বা, a2 -3a-2a+6 =0
বা, a(a-3)-2(a-3) =0
বা, (a-3)(a-2) =0
দুটি রাশির গুনফল শূন্য
∴ (a-3) =0
বা, a = 3
অথবা , (a-2) =0
বা, a = 2
∴ a= 2 এবং a = 3
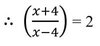
বা, x+4 = 2x-8
বা, x-2x = -4-8
বা, -x = -12
বা, x = 12
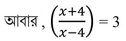
বা, x+4 = 3x-12
বা, x-3x = -4-12
বা, -2x = -16
বা, x = -16/-2
বা, x = 8
নির্ণেয় সমাধান x = 12 এবং x = 8
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
(b) দুই অঙ্ক বিশিষ্ট একটি সংখ্যার একক স্থানীয় অঙ্কটি দশক স্থানীয় অঙ্ক অপেক্ষা 6 বেশী এবং অঙ্কদ্বয়ের গুনফল সংখাটির চেয়ে 12 কম । সংখ্যাটির এককের অঙ্ক কী কী হতে পারে ?
সমাধানঃ ধরি , সংখ্যাটির দশক স্থানীয় অঙ্ক x
∴ সংখ্যাটির একক স্থানীয় অঙ্ক হবে (x+6)
সুতরাং সংখ্যাটি হবে = 10x+(x+6) = 11x+6
শর্তানুসারে ,
(11x+6) –x(x+6) = 12
বা, 11x+6 –x2-6x -12 =0
বা, 5x-x2 -6 =0
বা, -x2 +5x-6=0
বা, -(x2-5x+6) =0
বা, x2 -5x+6 = 0
বা, x2 –(3+2)x+6=0
বা, x2 -3x-2x+6=0
বা, x(x-3)-2(x-3)=0
বা, (x-3)(x-2) = 0
দুটি রাশির গুনফল শূন্য
∴ (x-3) =0
বা, x = 3
অথবা
(x-2) =0
বা, x= 2
∴ দশকের অঙ্কগুলি হল (2+6) =8 বা (3+6)=9
∴ সংখ্যাটির এককের ঘরের অঙ্কগুলি হবে 8 বা 9 ।
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
7.
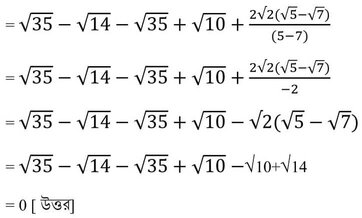
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
(b) x ∝ y এবং y ∝ z হলে , প্রমাণ করোঃ (x2+y2+z2) ∝ (xy+yz+zx)
সমাধানঃ x ∝ y
∴ x = Ay [ A একটি অশূন্য ভেদ ধ্রুবক ]
আবার y ∝ z
∴ y = Bz [B একটি অশূন্য ভেদ ধ্রুবক ]
∴ x = Ay = A(Bz) = ABz = Cz [AB =C =অশূন্য ভেদ ধ্রুবক ]
∴ x = Cz এবং y =Bz
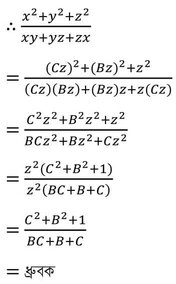
∴ (x2+y2+z2) ∝ (xy+yz+zx) [প্রমাণিত ]
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।
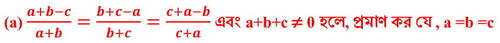
সমাধানঃ
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
(b)x:a = y:b = z:c হলে প্রমান করি যে , (a2+b2+c2)(x2+y2+z2) = (ax+by+cz)2
ধরি , x:a = y:b = z:c = k [ k (≠0) একটি আনুপাতিক ধ্রুবক ]
∴ x= ak , y=bk, z = ck
বামপক্ষঃ
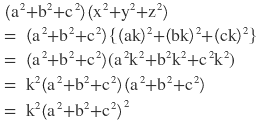
ডানপক্ষঃ
(ax+by+cz)2
= {a(ak)+b(bk)+c(ck)}2
= (a2k+b2k+c2k)2
= k2(a2+b2+c2)2
∴ বামপক্ষ = ডানপক্ষ [ প্রমানিত ]
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
9.
(a) প্রমাণ কর একটি সমকোণী ত্রিভুজের সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্ব অংকন করলে লম্বের দুপাশে যে দুটি ত্রিভুজ উৎপন্ন হয় ,তারা মূল ত্রিভুজের সঙ্গে সদৃশ এবং পরস্পর সদৃশ ।
দশম শ্রেণির গণিত পাঠ্য বই (গণিত প্রকাশ ) -এর 48 নম্বর উপপাদ্য দেখ ।
(b) প্রমান কর কোনো বৃত্তের স্পর্শক ও স্পর্শবিন্দুগামী ব্যাসার্ধ পরস্পর লম্ব ।
দশম শ্রেণির গণিত পাঠ্য বই (গণিত প্রকাশ ) -এর 40 নম্বর উপপাদ্য দেখ ।
10.
(a) ABC ত্রিভুজের BC বাহুর ওপর AD লম্ব এবং AD2 = BD.DC;প্রমাণ কর যে ∠BAC একটি সমকোণ ।
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
(b) একটি সরলরেখা দুটি এক কেন্দ্রীয় বৃত্তের একটিকে A ও B বিন্দুতে এবং অপরটিকে C ও D বিন্দুতে ছেদ করেছে । প্রমাণ কর AC =BD .
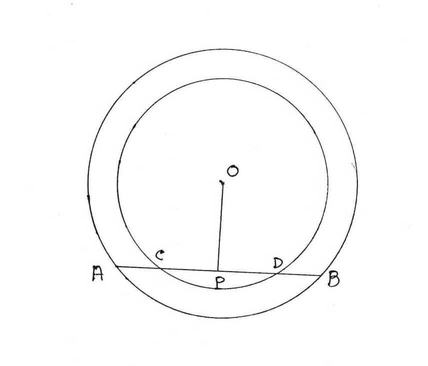
চিত্রে O কেন্দ্রীয় দুটি বৃত্তকে একটি সরলরেখা যথাক্রমে A,B এবং C,D বিন্দুতে ছেদ করেছে ।
প্রমান করতে হবে যে AB = CD ।
অঙ্কনঃ O থেকে AB এর ওপর একটি লম্ব OP অঙ্কন করা হল ।
প্রমানঃ যেহেতু বৃত্তের কেন্দ্রগামী কোনও জ্যা এর ওপর অঙ্কিত লম্ব জ্যা টিকে সমদ্বিখন্ডিত করে । তাই P ,AB এবং CD উভয়ের মধ্যবিন্দু ।
∴ AP=PB এবং CP=PD
সুতরাং AP-CP= PB-PD
∴ AC=DB (প্রমানিত)
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
11.
(a) 4 সেমি. ও 2 সেমি. ব্যাসার্ধ বিশিষ্ট দুটি বৃত্ত অংকন কর যাদের কেন্দ্রদ্বয়ের মধ্যে দূরত্ব 7 সেমি. । ওই বৃত্ত দুটির একটি সরল সাধারণ স্পর্শক অংকন কর । (কেবলমাত্র অংকন চিহ্ন দিতে হবে )
সমাধানঃ
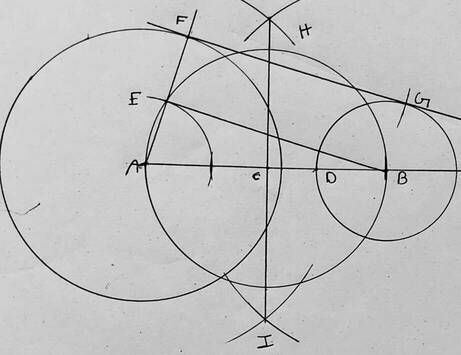
FG হল নির্ণেয় সরল সাধারণ স্পর্শক ।
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
(b) একটি ত্রিভুজ অংকন কর যাদের দুটি বাহুর দৈর্ঘ্য 9 সেমি. ও 7 সেমি. এবং তাদের অন্তর্ভুক্ত কোণ 60° ; ত্রিভুজটির অন্তবৃত্ত অঙ্কন কর ।(কেবলমাত্র অঙ্কন চিহ্ন দিতে হবে )।
সমাধানঃ
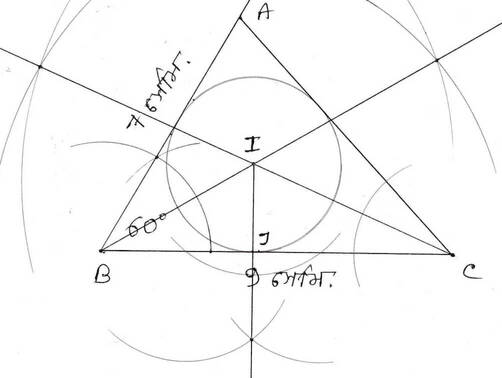
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
12.
(a) একটি বৃত্তের 220 সেমি. দৈর্ঘ্যের বৃত্তচাপ বৃত্তের কেন্দ্রে 60° কোণ উৎপন্ন করলে , বৃত্তের ব্যাসার্ধের দৈর্ঘ্য নির্ণয় কর ।
সমাধানঃ
∴ বৃত্তের ব্যাসার্ধ 210 সেমি. ।
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
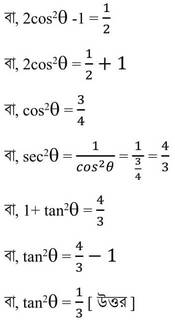
∴ tan2ϴ = 1/3
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
Madhyamik 2018 Math Question Solution/মাধ্যমিক ২০১৮ গণিত সমাধান
13.
(a) সূর্যের উন্নতি কোণ 45° থেকে বৃদ্ধি পেয়ে 60° হলে , একটি খুঁটির ছায়ার দৈর্ঘ্য 3 মিটার কমে যায় । খুঁটির উচ্চতা নির্ণয় কর ।
সমাধানঃ
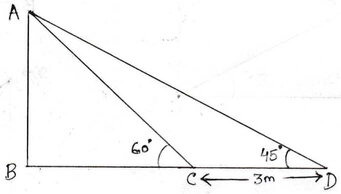
ধরাযাক , AB হল খুঁটির দৈর্ঘ্য । যখন সূর্যের উন্নতি কোণ 45° হলে খুঁটির ছায়ার দৈর্ঘ্য BD এবং সূর্যের উন্নতি কোণ 60° হলে খুঁটির ছায়ার দৈর্ঘ্য হয় BC , অর্থাৎ খুঁটির ছায়ার দৈর্ঘ্য CD কমে যায় ।
∴ CD = 3 মিটার
ABC ত্রিভুজের ∠ABC=90° এবং ∠ACB =60°
এখন ABC সমকোণী ত্রিভুজ থেকে পাই ,
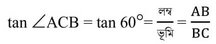
(b) 20. 5√3 মিটার উঁচু রেলওয়ে ব্রিজে দাঁড়িয়ে একব্যাক্তি প্রথমে একটি ট্রেনের ইঞ্জিনকে ব্রিজের এপারে 30° অবনতি কোণে দেখলেন । কিন্তু 2 সেকেন্ড পরই ওই ইঞ্জিনকে ব্রিজের ওপারে 45° অবনতি কোণে দেখলেন । ট্রেনটির গতিবেগ কত ?
সমাধানঃ
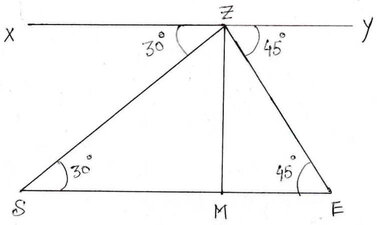
ধরি , ওই ব্যাক্তি XY রেলওয়ে ওভারব্রিজের Z বিন্দুতে দাঁড়িয়ে ট্রেনের ইঞ্জিনকে প্রথমে S বিন্দুতে এবং 2 সেকেন্ড পরে E বিন্দুতে দেখলেন । অবনতি কোণ ∠BAS =30° এবং ∠CAE =45°
ZM = রেলওয়ে ওভারব্রিজের উচ্চতা = 5√3 মিটার
আবার যেহেতু XY||SE
∴ ∠ZSM = একান্তর ∠XZS = 30°
এবং ∠ZEM = একান্তর ∠YZE =45°
সমকোণী ত্রিভুজ ZSM থেকে পাই,
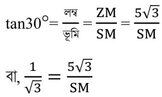
বা, SM = 15
সমকোণী ত্রিভুজ ZEM থেকে পাই
বা, ME =5√3
∴ SE = SM+ME =(15+5√3)=15+5´1.732 =15+8.660=23.660
∴ 2 সেকেন্ডে ট্রেনটি অতিক্রম করে 23.660 মিটার ।
14.
(a) একটি ঘনকের প্রতিটি বাহুকে 50% কমানো হল । মূল ঘনক ও পরিবর্তিত ঘনকের ঘনফলের অনুপাত কত ?
সমাধানঃ ধরি ঘনকের প্রতিটি বাহুর দৈর্ঘ্য a একক
∴ ঘনকটির ঘনফল = a3 ঘনএকক
প্রতিটি বাহুর দৈর্ঘ্য 50% কমানো হলে, পরিবর্তিত ঘনকের প্রতিটি বাহুর দৈর্ঘ্য
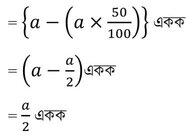
পরিবর্তিত ঘনকের ঘনফল
সুতরাং মূল ঘনক এবং পরিবর্তিত ঘনকের ঘনফলের অনুপাত
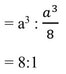
∴ মূল ঘনক ও পরিবর্তিত ঘনকের অনুপাত 8:1 ।
(b) একমুখ খোলা একটি লম্ব বৃত্তাকার পাত্রের সমগ্রতলের ক্ষেত্রফল 2002 বর্গ সেমি. । পাত্রটির ভূমির ব্যাসের দৈর্ঘ্য 14 সেমি. হলে , পাত্রটিতে কত লিটার জল ধরবে হিসাব করে লিখি ।
সমাধানঃ একমুখ খোলা একটি লম্ব বৃত্তাকার পাত্রের ভূমির ব্যাসের দৈর্ঘ্য 14 সেমি.
∴ ব্যাসার্ধ (r ) = 14/2 সেমি.= 7 সেমি.
ধরি, লম্ব বৃত্তাকার পাত্রের উচ্চতা = h সেমি.
একমুখ খোলা পাত্রটির সমগ্রতলের ক্ষেত্রফল
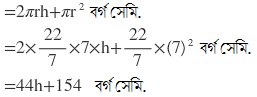
শর্তানুসারে ,
44h+154=2002
বা, 44h=2002-154
বা,44h = 1848
বা, h = 42
∴ পাত্রটির উচ্চতা 42 সেমি. ।
∴ পাত্রটির আয়তন
উত্তরঃ পাত্রটিতে জল ধরে 6.468 লিটার ।
(c) 21 ডেসিমি. দীর্ঘ , 11 ডেসিমি. প্রশস্থ এবং 6 ডেসিমি. গভীর একটি চৌবাচ্চা অর্ধেক জলপূর্ণ আছে । এখন সেই চৌবাচ্চায় যদি 21 সেমি. ব্যাসের 100 টি লোহার গোলক সম্পূর্ণ ডুবিয়ে দেওয়া হয়, তবে জলতল কতটা উপরে উঠবে তা হিসাব করে লিখি ।
সমাধানঃ ধরি, 21 ডেসিমি. দীর্ঘ , 11 ডেসিমি. প্রশস্থ এবং 6 ডেসিমি. গভীর একটি চৌবাচ্চায় 21 সেমি. ব্যাসের 100 টি লোহার গোলক সম্পূর্ণ ডুবিয়ে দিলে জলতল h সেমি. উঠবে ।
লোহার গোলকের ব্যাসের দৈর্ঘ্য 21 সেমি.
∴ লোহার গোলকের ব্যাসার্ধ (r ) = 21/2 সেমি.= 21/20 ডেসিমি.
এখন , h উচ্চতার জলস্তম্ভের আয়তন =100 টি লোহার গোলকের আয়তন
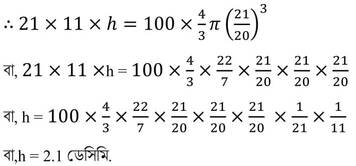
∴ চৌবাচ্চার জলতল 2.1 ডেসিমি. উপরে উঠবে ।
15.
(a) একটি প্রবেশিকা পরিক্ষায় পরীক্ষার্থীর বয়সের পরিসংখ্যা বিভাজন ছক থেকে সংখ্যাগুরু মান নির্ণয় করি ।
| বয়স ( বছরে ) | 16-18 | 18-20 | 20-22 | 22-24 | 24-26 |
| পরীক্ষার্থীর সংখ্যা | 45 | 75 | 38 | 22 | 20 |
সমাধান ঃপ্রদত্ত পরিসংখ্যা বিভাজনের সংখ্যাগুরু মানের শ্রেণী = 18-20
সংখ্যাগুরু মান নির্ণয়ের সূত্রটি হলো
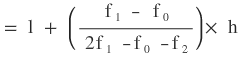
যেখানে,
l হলো সংখ্যাগুরুমান সংবলিত শ্রেণীর নিম্ন শ্রেণী সীমানা ।
h = সংখ্যাগুরু মান সংবলিত শ্রেণীর শ্রেণী দৈর্ঘ্য ।
f1 = সংখ্যাগুরুমান সংবলিত শ্রেণীর শ্রেণী পরিসংখ্যা ।
f0 = সংখ্যাগুরুমান সংবলিত শ্রেণীর ঠিক পূর্ববর্তী শ্রেণীর পরিসংখ্যা ।
f2 = সংখ্যাগুরুমান সংবলিত শ্রেণীর ঠিক পরবর্তী শ্রেণীর পরিসংখ্যা ।
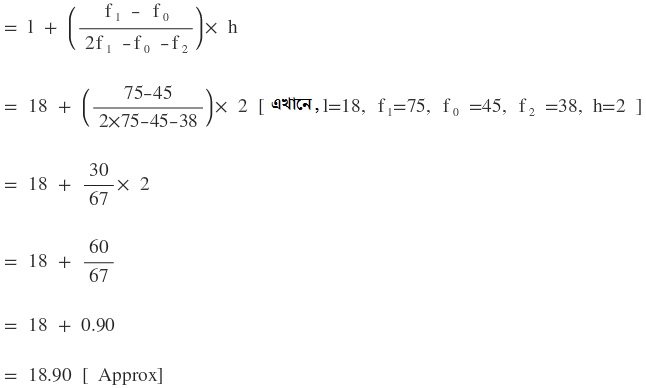
মাধ্যমিকের সকল বিষয়ের বিগত বছরের প্রশ্ন উত্তর (Click Here)
(b) নীচের তথ্যের মধ্যমা নির্ণয় করি ।
| শ্রেণী সীমা | 1-5 | 6-10 | 11-15 | 16-20 | 21-25 | 26-30 | 31-35 |
| পরিসংখ্যা | 2 | 3 | 6 | 7 | 5 | 4 | 3 |
সমাধানঃ
প্রদত্ত পরিসংখ্যা বিভাজনের ছকের শ্রেণীগুলি শ্রেণী অন্তর্ভুক্ত গথনে আছে ।
শ্রেণী বহির্ভূত পরিসংখ্যা বিভাজনের তালিকা তৈরি করি ,
| শ্রেণী– সীমা | শ্রেণী –সীমানা | পরিসংখ্যা | ক্রম–যৌগিক পরিসংখ্যা ( ক্ষুদ্রতর সূচক ) |
| 1-5 | 0.5-5.5 | 2 | 2 |
| 6-10 | 5.5-10.5 | 3 | 5 |
| 11-15 | 10.5-15.5 | 6 | 11 |
| 16-20 | 15.5-20.5 | 7 | 18 |
| 21-25 | 20.5-25.5 | 5 | 23 |
| 26-30 | 25.5-30.5 | 4 | 27 |
| 31-35 | 30.5-35.5 | 3 | 30 = n |
এখানে n = 30
∴ n/2 = 30/2 = 15
15 এর থেকে ঠিক বেশি পরিসংখ্যা বিশিষ্ট শ্রেণী টি হলো (15.5-20.5)
∴ মধ্যমা শ্রেণী টি হলো = 15.5 – 20.5
∴ মধ্যমা নির্ণয়ের সূত্র টি হলো
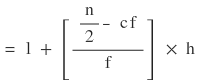
l = মধ্যমা শ্রেণীর নিম্ন শ্রেণী সীমানা ।
n = মোট পরিসংখ্যা ।
f = মধ্যমা শ্রেণীর পরিসংখ্যা ।
h = শ্রেণী দৈর্ঘ্য ।
cf = মধ্যমা শ্রেণীর পূর্বের শ্রেণীর পরিসংখ্যা ।
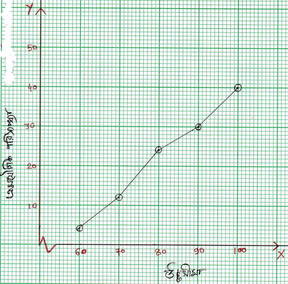
(iii) নীচের পরিসংখ্যা বিভাজনের ক্ষুদ্রতর সুচক ওজাইভ অঙ্কন করঃ
| প্রাপ্ত নম্বর | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| পরিসংখ্যা | 4 | 8 | 12 | 6 | 10 |
সমাধানঃ
| শ্রেণি | ক্ষুদ্রতর সূচক ক্রমযৌগিক পরিসংখ্যা |
| 60 এর কম | 4 |
| 70 এর কম | 12 |
| 80 এর কম | 24 |
| 90 এর কম | 30 |
| 100 এর কম | 40 |
X অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 1 টি বাহুর দৈর্ঘ্য = 1 একক এবং y অক্ষ বরাবর ক্ষুদ্রতম বর্গক্ষেত্রের 1 টি বাহুর দৈর্ঘ্য = 1 একক ধরে
(60,4) ,(70,12) , (80,24) ,(90,30) ,(100,40) বিন্দুগুলি স্থাপন করে ও যুক্ত করে ক্ষুদ্রতর সুচক ওজাইভ অঙ্কন কর ।
ধন্যবাদ । POST টি ভাল লেগে থাকলে SHARE করার অনুরোধ রইল ।