বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.2|Koshe Dekhi 15.2 Class 10|গণিত প্রকাশ দশম শ্রেণি (ক্লাস১০)(টেন) কষে দেখি ১৫.২ সমাধান |Theorems Related To Tangent To a Circle|WBBSE Madhyamik Ganit Prakash Class 10 (Ten)(X) Koshe Dekhi 15.2 Chapter 15.
দশম শ্রেণীর গণিত প্রকাশ বইএর সব অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.2।Koshe Dekhi 15.2 Class 10|কষে দেখি 15.2 ক্লাস 10
1. 16 সেমি. দৈর্ঘ্যের ব্যাস বিশিষ্ট একটি বৃত্তের কেন্দ্র থেকে 17 সেমি. দূরত্বে অবস্থিত একটি বিন্দু থেকে অঙ্কিত বৃত্তের স্পর্শকের দৈর্ঘ্য হিসাব করে লিখি ।
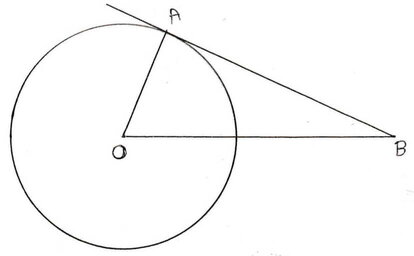
সমাধানঃ ∆OAB ত্রিভুজে, OB = 17 সেমি. এবং ব্যাসার্ধ OA = 8 সেমি.
OA স্পর্শবিন্দুগামী ব্যাসার্ধ ।
OA ⊥ AB
এখন , ∆OAB সমকোণী ত্রিভুজ থেকে পাই ,
OB2 = OA2+AB2 [ পিথাগোরাসের উপপাদ্য অনুসারে ]
বা, (17)2 = (8)2+AB2
বা, AB2 = 289-64
বা, AB2 = 225
বা, AB = √225
বা, AB = 15
∴ AB স্পর্শকের দৈর্ঘ্য 15 সেমি.।
2. একটি বৃত্তের উপর P ও Q বিন্দু দুটিতে অঙ্কিত স্পর্শক দুটি A বিন্দুতে ছেদ করেছে , ∠PAQ =60° হলে ∠APQ এর মান নির্ণয় করি ।
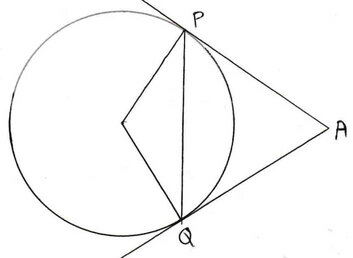
বহিঃস্থ বিন্দু A থেকে দুটি স্পর্শক AP ও AQ অঙ্কন করা হল । ∠PAQ = 60° হলে ∠APQ এর মান নির্ণয় করতে হবে ।P,Q যুক্ত করা হল ।
যেহেতু , বহিঃস্থ বিন্দু A থেকে দুটি স্পর্শক AP ও AQ অঙ্কন করা হয়েছে ,
∴ AP=AQ
∴ ∠APQ = ∠AQP
আবার , ∠PAQ = 60°
∴ ∠APQ = ∠AQP = (180°-60°)/2 = 120°/2 =60°
∴ ∠APQ = 60°
3. O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু A থেকে অঙ্কিত দুটি স্পর্শক AP ও AQ বৃত্তকে P ও Q বিন্দুতে স্পর্শ করে । PR একটি ব্যাস হলে , প্রমান করি যে OA ∥ RQ ।
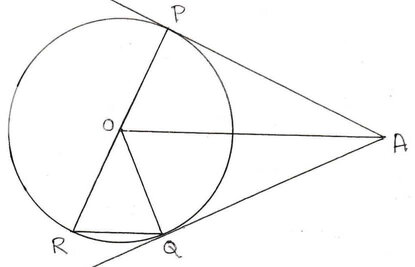
O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু A থেকে দুটি স্পর্শক AP ও AQ অঙ্কন করা হয়েছে যা বৃত্তকে P ও Q বিন্দুতে স্পর্শ করে । PR বৃত্তের ব্যাস । প্রমান করতে হবে যে , OA ∥ RQ
অঙ্কনঃ O,Q যুক্ত করা হল ।
প্রমাণঃ O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু A থেকে দুটি স্পর্শক AP ও AQ অঙ্কন করা হয়েছে । ∴ ∠AOP = ∠AOQ
আবার , ∆ORQ এর OR = OQ [ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠ORQ = ∠OQR
ORQ ত্রিভুজের , ∠ORQ+∠OQR = ∠POQ [ ∵ ত্রিভুজের কোনো বাহুকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোন অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান ]
∴ ∠ORQ+∠ORQ = ∠POQ [∵ ∠ORQ = ∠OQR]
বা, 2∠ORQ = ∠AOP+∠AOQ
বা, 2∠ORQ = ∠AOP+∠AOP [ ∵ ∠AOP=∠AOQ ]
বা, 2∠ORQ = 2∠AOP
বা, ∠ORQ = ∠AOP
আবার এরা অনুরূপ কোণ
সুতরাং , OA ∥ RQ [ প্রমানিত ]
4. প্রমান করি বৃত্তের পরিলিখিত কোনো চতুর্ভুজের যেকোনো দুটি বিপরীত বাহুর দ্বারা উৎপন্ন কেন্দ্রস্থ সম্মুখ কোন দুটি পরস্পর সম্পূরক ।
দুটি কোন পরস্পর সম্পূরক এর অর্থ দুটি কোণের সমষ্টি 2 সমকোণ
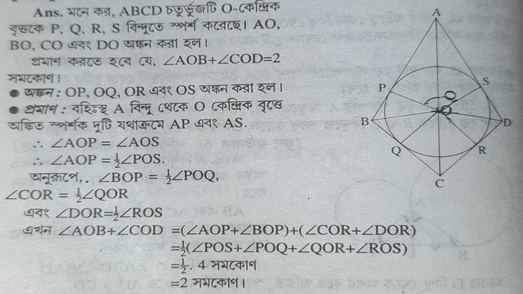
5.প্রমাণ করি যে বৃত্তে পরিলিখিত সামান্তরিক মাত্রই রম্বস ।
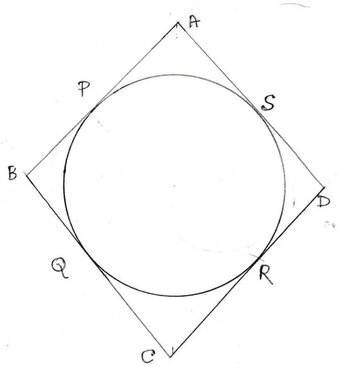
ধরাযাক,ABCD একটি বৃত্তের পরিলিখিত সামান্তরিক । আরও ধরাযাক ,ABCD সামান্তরিকটির AB,BC,CD,DA বাহুগুলি বৃত্তটিকে যথাক্রমে P ,Q,R,S বিন্দুতে স্পর্শ করে । প্রমাণ করতে হবে , ABCD একটি রম্বস ।
প্রমাণঃ P বিন্দু থেকে দুটি স্পর্শক PA ও PS অঙ্কন করা হয়েছে ।
∴ AP =AS
অনুরূপে , BP=BQ , CQ=CR এবং DR =DS
AB+CD = AP+BP+CR+DR
বা, AB+CD = AS+BQ+CQ+DS [ ∵ PA=AS,BP=BQ , CQ=CR এবং DR =DS]
বা, AB+CD = (AS+DS)+(BQ+CQ)
বা, AB+CD = AD+BC
বা, AB+AB = BC+BC [ ∵ ABCD একটি সামান্তরিক এবং AB=CD, AD=BC]
বা, 2AB = 2BC
বা, AB = BC
অর্থাৎ ABCD সামান্তরিকের দুটি সন্নিহিত বাহু সমান।
সুতরাং, ABCD একটি রম্বস (প্রমানিত)
দশম শ্রেণীর গণিত প্রকাশ বইএর সব অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
6.A ও B কেন্দ্রীয় দুটি বৃত্ত অঙ্কন করেছি যারা পরস্পরকে C বিন্দুতে বহিঃস্পর্শ করেছে । C বিন্দুতে অঙ্কিত স্পর্শকের উপর O একটি বিন্দু এবং OD ও OE যথাক্রমে A ও B কেন্দ্রীয় বৃত্তকে যথাক্রমে D ও E বিন্দুতে স্পর্শ করেছে । ∠COD = 56° , ∠COE = 40° ,∠ACD = x° এবং ∠BCE = y° হলে প্রমাণ করি যে OD =OC=OE এবং x-y = 8
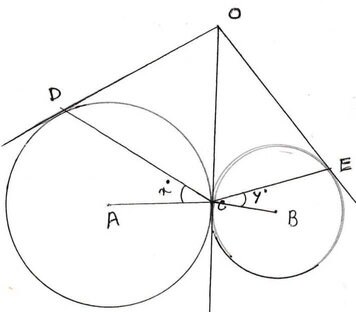
সমাধানঃ বহিঃস্থ বিন্দু O থেকে দুটি স্পর্শক OD এবং OC অঙ্কন করা হয়েছে
∴ OD =OC —- (i)
আবার , O বিন্দু থেকে দুটি স্পর্শক OC এবং OE অঙ্কন করা হয়েছে
∴ OC = OE —- (i)
∴ OD=OC=OE [প্রমানিত ]
এখন , ∆OCD এর ∠COD = 56°
এবং ∠OCD = ∠ODC [ ∵OC =OD]
∴ OCD = (180°-56°)/2=62°
আবার,∆OCE এর COE = 40°
এবং ∠OCE = ∠OEC
∴ ∠OCE =(180°-40°)/2 = 70°
এখন ,AC স্পর্শ বিন্দুগামী ব্যাসার্ধ
∴ ∠OCA = 90°
বা, ∠OCD+∠ACD = 90°
বা, 62°+∠ACD = 90°
বা, ∠ACD = 90°-62°=28°
বা, x =28°
আবার , BC স্পর্শবিন্দুগামী ব্যাসার্ধ
∴ ∠OCB = 90°
বা, ∠OCE+∠BCE = 90°
বা, 70+∠BCE = 90°
বা, ∠BCE = 90°-70°=20°
বা, y = 20°
∴ x-y = 28°-20°=8° [ প্রমানিত ]
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
7.A ও B কেন্দ্রবিশিষ্ট দুটি নির্দিষ্ট বৃত্ত পরস্পরকে অন্তঃস্পর্শ করেছে । অপর একটি বৃত্ত বৃহত্তর বৃত্তটিকে X বিন্দুতে অন্তঃস্পর্শ এবং ক্ষুদ্রতর বৃত্তটিকে Y বিন্দুতে বহিঃ স্পর্শ করেছে । O যদি ওই বৃত্তের কেন্দ্র হয় তবে প্রমাণ করি যে , AO +BO = ধ্রুবক
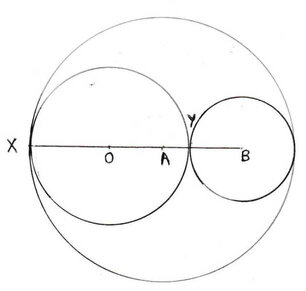
A ও B কেন্দ্রবিশিষ্ট দুটি নির্দিষ্ট বৃত্ত পরস্পরকে অন্তঃস্পর্শ করেছে । অপর একটি বৃত্ত বৃহত্তর বৃত্তটিকে X বিন্দুতে অন্তঃস্পর্শ এবং ক্ষুদ্রতর বৃত্তটিকে Y বিন্দুতে বহিঃ স্পর্শ করেছে । বৃত্তটির কেন্দ্র O হলে প্রমাণ করতে হবে যে AO +BO = ধ্রুবক ।
প্রমাণঃ যেহেতু , A কেন্দ্রীয় ও B কেন্দ্রীয় দুটি বৃত্ত নির্দিষ্ট সুতরাং তাদের ব্যাসার্ধের দৈর্ঘ্য নির্দিষ্ট । অর্থাৎ AX এবং BY প্রত্যেকে নির্দিষ্ট ।
∴ AX +BY = ধ্রুবক
∴ AO+BO
= AX-OX+OA+AB
= AX-OX+OA+AY+YB
= AX-OX+OY+YB [OA+AY =OY]
= AX –OX+OX+YB [∵ OX=OY , একই বৃত্তের ব্যাসার্ধ ]
= AX +YB
= ধ্রুবক
∴ AO+BO= ধ্রুবক [ প্রমানিত ]
8. A ও B কেন্দ্রীয় দুটি বৃত্ত অঙ্কন করেছি যারা পরস্পরকে O বিন্দুতে বহিঃস্পর্শ করেছে । O বিন্দু দিয়ে একটি সরলরেখা অঙ্কন করেছি যা বৃত্ত দুটিকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে । প্রমান করি যে AP ∥ BQ .
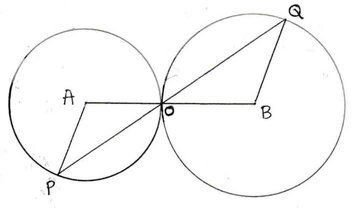
মনেকরি , P এবং Q কেন্দ্রিক বৃত্তদুটি পরস্পরকে বহিঃস্থ ভাবে O বিন্দুতে স্পর্শ করেছে । O বিন্দুগামী একটি সরলরেখা A ও B কেন্দ্রিক বৃত্তদুটিকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে । প্রমান করতে হবে যে, AP ∥ BQ
অঙ্কনঃ A,P;B,Q যুক্ত করা হল ।
প্রমাণঃ ∠AOP = বিপ্রতীপ ∠BOQ
আবার , ∆APO এর AP = AO
∴ ∠AOP = ∠APR
অনুরূপে , ∠BQO –এর ∠BOQ = ∠BQO
∴ ∠APO = ∠BQO
কিন্তু এরা একান্তর কোণ ।
∴ AP ∥ BQ [প্রমাণিত ]
বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.2।Koshe Dekhi 15.2 Class 10|কষে দেখি ১৫.২ ক্লাস ১০
9. তিনটি সমান বৃত্ত পরস্পরকে বহিঃস্পর্শ করেছে ।প্রমান করি যে ওই বৃত্ত তিনটির কেন্দ্রগুলি একটি সমবাহু ত্রিভুজের শীর্ষবিন্দু ।

10. একটি বৃত্তের বহিঃস্থ কোনো বিন্দু A থেকে অঙ্কিত AB ও AC দুটি স্পর্শক বৃত্তকে B ও C বিন্দুতে স্পর্শ করে । উপচাপ BC এর উপর অবস্থিত X বিন্দুতে অঙ্কিত স্পর্শক AB ও AC কে যথাক্রমে D ও E বিন্দুতে ছেদ করে । প্রমান করি যে ∆ADE-এর পরিসীমা = 2AB
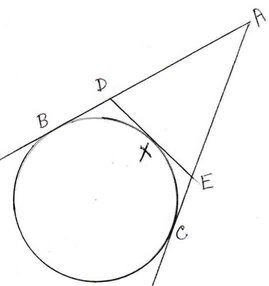
প্রমাণঃ বহিঃস্থ বিন্দু A থেকে দুটি স্পর্শক AB ও AC অঙ্কন করা হয়েছে ।
∴ AB =AC [∵ বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে অঙ্কিত স্পর্শক দুটির দৈর্ঘ্য সমান ]
আবার , D বিন্দু থেকে দুটি স্পর্শক DB ও DX অঙ্কন করা হয়েছে
∴ DB = DX [∵ বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে অঙ্কিত স্পর্শক দুটির দৈর্ঘ্য সমান ]
এবং E বিন্দু থেকে দুটি স্পর্শক EX ও EC অঙ্কন করা হয়েছে
∴ EX =EC [∵ বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে অঙ্কিত স্পর্শক দুটির দৈর্ঘ্য সমান ]
∴ ∆ADE এর পরিসীমা = AD+DE+AE
= AD+DX+EX+AE
= AD+DB+EC+AE [∵ DX =DB এবং EX=EC]
= AB+AC
= AB+AB [ AC =AB]
= 2AB
∴ ∆ADE এর পরিসীমা =2AB [প্রমানিত ]
দশম শ্রেণীর গণিত প্রকাশ বইএর সব অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
11. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন(V.S.A.)
(A) বহু বিকল্পীয় প্রশ্ন(M.C.Q)
(i) O কেন্দ্রীয় বৃত্তের বহিঃস্থ A বিন্দু থেকে অঙ্কিত স্পর্শক বৃত্তকে B বিন্দুতে স্পর্শ করে । OB= 5 সেমি. , AO = 13 সেমি. হলে ,AB এর দৈর্ঘ্য
(a) 12 সেমি.
(b) 13 সেমি.
(c ) 6.5 সেমি.
(d) 6 সেমি.
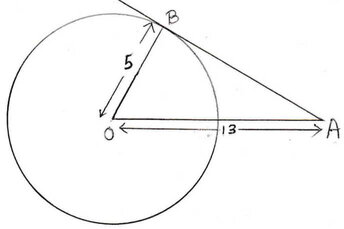
Ans: (a) 12 সেমি.
সমাধানঃ ত্রিভুজ ∆AOB এর ক্ষেত্রে , ∠OBA = 90 [ ∵ OB স্পর্শবিন্দুগামী ব্যাসার্ধ ]
OB = 5 সেমি.
OA = 13 সেমি
এখন সমকোণী ত্রিভুজ ∆AOB তে পিথাগরাসের উপপাদ্য প্রয়োগ করে পাই ,
OA2= OB2+AB2
বা, (13)2 = (5)2+AB2
বা, 169=25+AB2
বা, AB2 = 169-25
বা, AB2 = 144
বা, AB2 = (12)2
বা, AB = 12
অর্থাৎ,স্পর্শকের দৈর্ঘ্য 12 সেমি.
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
(ii) দুটি বৃত্ত পরস্পরকে C বিন্দুতে বহিঃস্পর্শ করেছে । AB বৃত্তদুটির একটি সাধারন স্পর্শক বৃত্ত দুটিকে A ও B বিন্দুতে স্পর্শ করে । ∠ACB এর পরিমান
(a) 60°
(b) 45°
(c) 30°
(d) 90°
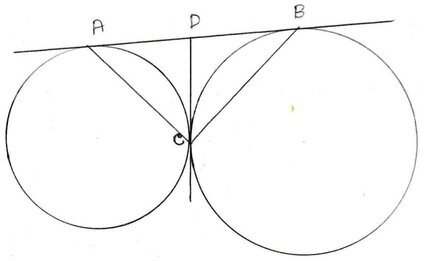
Ans: (d) 90°
সমাধানঃ C বিন্দু থেকে একটি সরলরেখা অঙ্কন করা হল যা, AB স্পর্শক কে D বিন্দুতে ছেদ করে ।
∴ DA = DC [ ∵ বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে অঙ্কিত স্পর্শক দুটির দৈর্ঘ্য সমান ]
∴ ∠DAC =∠DCA
আবার , DC =DB [ ∵ বৃত্তের বহিঃস্থ কোনো বিন্দু থেকে অঙ্কিত স্পর্শক দুটির দৈর্ঘ্য সমান ]
∴ ∠DCB =∠DBC
∆ACB ত্রিভুজ থেকে পাই ,
∠BAC + ∠ABC+ ∠ACB = 180°
বা, ∠DAC+∠DCA+∠DCB+∠DBC=180°
বা, ∠DCA+∠DCA+∠DCB+∠DCB=180° [∵∠DAC =∠DCA এবং ∠DCB =∠DBC ]
বা, 2∠DCA+2∠DCB = 180°
বা, 2(∠DCA+∠DCB)=180°
বা, 2∠ACB = 180°
বা, ∠ACB = 180/2= 90°
(iii) O কেন্দ্রীয় বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি. । O বিন্দু থেকে 13সেমি দুরত্বে P একটি বিন্দু । P বিন্দু থেকে বৃত্তের দুটি স্পর্শকের দৈর্ঘ্য PQ এবং PR ; PQOR চতুর্ভুজের ক্ষেত্রফল
(a) 60 বর্গ সেমি.
(b) 30 বর্গ সেমি.
(c ) 120 বর্গ সেমি.
(d) 150 বর্গ সেমি.
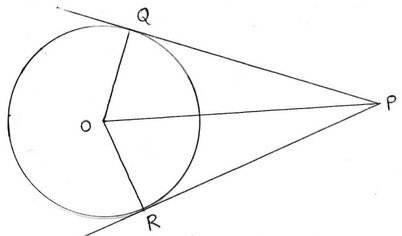
Ans: (a) 60 বর্গ সেমি.
সমাধানঃ ∆OPR ত্রিভুজে OR = 5 সেমি. ( বৃত্তের ব্যাসার্ধ ) , OP = 13 সেমি.
যেহেতু OR স্পর্শবিন্দুগামী ব্যাসার্ধ ∴ OR ⊥ PR
∴ সমকোণী ত্রিভুজ ∆OPR থেকে পাই ,
OR2+PR2=OP2
বা, (5)2+PR2=(13)2
বা, PR2 = 169-25
বা, PR2 = 144
বা , PR2= (12)2
বা, PR = 12
যেহেতু , PR এবং PQ দুটি স্পর্শক এবং P বহিঃস্থ বিন্দু
∴ PR = PQ = 12 সেমি.
PQOR চতুর্ভুজের ক্ষেত্রফল = ত্রিভুজ ∆POR এর ক্ষেত্রফল + ত্রিভুজ ∆POQ এর ক্ষেত্রফল
= ½ ✕ 12 ✕ 5 + ½ ✕ 12 ✕ 5 বর্গ সেমি. [ ∵সমকোণী ত্রিভুজের ক্ষেত্রফল =½✕ ভুমি ✕ উচ্চতা ]
= (30+30) বর্গ সেমি.
= 60 বর্গ সেমি.
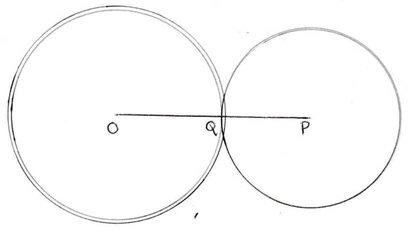
(iv) দুটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি. ও 3 সেমি. । বৃত্ত দুটি পরস্পরকে বহিঃস্পর্শ করে । বৃত্ত দুটির কেন্দ্র দ্বয়ের মধ্যে দূরত্ব
(a) 2 সেমি.
(b) 2.5 সেমি.
(c ) 1.5 সেমি.
(d) 8 সেমি.
Ans: (d) 8 সেমি.
সমাধানঃ OP = OQ+QP = (5+3) সেমি. = 8 সেমি.
বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.2।Koshe Dekhi 15.2 Class 10|কষে দেখি ১৫.২ ক্লাস ১০
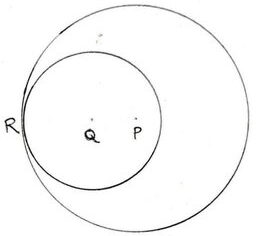
(v) দুটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 3.5 সেমি ও 2 সেমি. ।বৃত্তদুটি পরস্পরকে অন্তঃস্পর্শ করে । বৃত্ত দুটির কেন্দ্রদ্বয়ের মধ্যে দূরত্ব
(a) 5.5 সেমি.
(b) 1 সেমি.
(c ) 1.5 সেমি.
(d) কোনোটিই নয়
Ans: (c ) 1.5 সেমি.
সমাধানঃ PQ = PR-QR = (3.5 -2)সেমি. = 1.5 সেমি.
(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখিঃ
(i) একটি বৃত্তের অন্তঃস্থ একটি বিন্দু P ; বৃত্তে অঙ্কিত কোনো স্পর্শক P বিন্দুগামী নয় ।
উত্তরঃ সত্য
(ii) একটি বৃত্তে একটি নির্দিষ্ট সরলরেখা সমান্তরাল দুইএর অধিক স্পর্শক অঙ্কন করা যায় ।
উত্তরঃ মিথ্যা ।
Madhyamik Math Solution Of Chapter 15
(C ) শূন্যস্থান পূরণ করিঃ
(i) একটি সরলরেখা বৃত্তকে দুটি বিন্দুতে ছেদ করলে সরলরেখাটি বৃত্তের ________ বলে।
উত্তরঃ ছেদক
(ii)দুটি বৃত্ত পরস্পরকে ছেদ বা স্পর্শ না করলে বৃত্তদুটির সর্বাধিক সংখ্যায় _______ টি সাধারন স্পর্শক অঙ্কন করা যায় ।
উত্তরঃ 4
(iii) দুটি বৃত্ত পরস্পরকে A বিন্দুতে বহিঃস্পর্শ করে । A বিন্দুতে অঙ্কিত বৃত্ত দুটির সাধারন স্পর্শক হোলো_____________ সাধারন স্পর্শক ( সরল / তির্যক ) ।
উত্তরঃ তির্যক
বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.2।Koshe Dekhi 15.2 Class 10|কষে দেখি ১৫.২ ক্লাস ১০
12. সংক্ষিপ্ত উত্তরধর্মী প্রশ্নঃ
(i) পাশের চিত্রে বৃত্তের কেন্দ্র O এবং BOA বৃত্তের ব্যাস । বৃত্তের P বিন্দুতে অঙ্কিত স্পর্শক বর্ধিত BA কে T বিন্দুতে ছেদ করে । ∠PBO = 30° হলে ∠PTA এর মান নির্ণয় করি ।
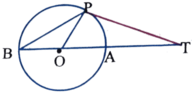
সমাধানঃ ত্রিভুজ ∆OPB তে OP=OB [ একই বৃত্তের ব্যাসার্ধ ]
এবং, ∠PBO = 30°
∴ ∠BPO = 30°
∆OPB এর , বহিঃস্থ কোন ∠AOP অন্তঃস্থ বিপরীত কোণদ্বয়ের (∠OPB এবং ∠OBP) এর সমষ্টির সমান ।
∴ ∠AOP = ∠OPB+∠OBP = 30°+30°=60°
∴ ∠POT = 60°
আবার , ∠OPA = 90° [ যেহেতু , OP স্পর্শবিন্দুগামী ব্যাসার্ধ ]
∴ ∠PTO = 180°-(∠POT+∠OPT) = 180°-(60°+90°)=180°-150°=30°
∠PTO = 30° [ উত্তর ]
বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.2।Koshe Dekhi 15.2 Class 10|কষে দেখি ১৫.২ ক্লাস ১০
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
(ii) পাশের চিত্রে ABC ত্রিভুজটি একটি বৃত্তে পরিলিখিত এবং বৃত্তকে P,Q,R বিন্দুতে স্পর্শ করে । যদি AP = 4 সেমি. , BP = 6 সেমি. , AC = 12 সেমি. এবং BC = x সেমি. হয় । তাহলে x এর মান নির্ণয় কর ।
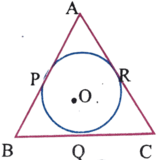
সমাধানঃ বহিঃস্থ কোনো বিন্দু থেকে বৃত্তের ওপর যে দুটি স্পর্শক অঙ্কন করা যায় তাদের দৈর্ঘ্য সমান ।
∴ AP=AR = 4 সেমি.
আবার , AC = 12 সেমি.
∴ RC = AC-AR = 12-4 = 8 সেমি.
∴ QC = 8 সেমি.
আবার, BP =6 সেমি. ∴ BQ = 6 সেমি. [বহিঃস্থ কোনো বিন্দু থেকে বৃত্তের ওপর যে দুটি স্পর্শক অঙ্কন করা যায় তাদের দৈর্ঘ্য সমান । ]
∴ x = BC = BQ+QC = (6+8)সেমি. = 14 সেমি.
∴ x = 14 সেমি.(উত্তর)
বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.2।Koshe Dekhi 15.2 Class 10|কষে দেখি ১৫.২ ক্লাস ১০
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
(iii) পাশের চিত্রে A,B,C কেন্দ্র বিশিষ্ট তিনটি বৃত্ত পরস্পরকে বহিঃস্পর্শ করে ।যদি AB = 5সেমি. , BC = 7 সেমি. এবং CA = 6 সেমি. হয় তাহলে A কেন্দ্রবিশিষ্ট বৃত্তের ব্যাসার্ধের দৈর্ঘ্য নির্ণয় কর ।
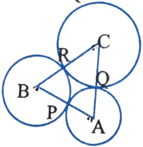
সমাধানঃ ধরি , A কেন্দ্র বিশিষ্ট বৃত্তের ব্যাসার্ধ r সেমি.
∴ AP=AQ= r সেমি.
AC = 6 সেমি. ( প্রদত্ত)
∴ CQ = AC-AQ = (6-r)সেমি.
∴ CR = (6-r) সেমি.[ ∵ CQ এবং CR একই বৃত্তের ব্যাসার্ধ ]
AB = 5 সেমি. ( প্রদত্ত)
∴ PB = AB-AP= (5-r) সেমি.
∴ BR =(5-r) সেমি.[ ∵ BP এবং BR একই বৃত্তের ব্যাসার্ধ ]
এখন , BC = 7
বা, BR+RC = 7
বা, 5-r+6-r =7
বা, 11-2r = 7
বা, 2r = 4
বা, r = 4/2
বা, r = 2
∴ A কেন্দ্র বিশিষ্ট বৃত্তের ব্যাসার্ধ 2 সেমি । (উত্তর)
বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.2।Koshe Dekhi 15.2 Class 10|কষে দেখি ১৫.২ ক্লাস ১০
(iv) পাশের চিত্রে O কেন্দ্রবিশিষ্ট বৃত্তে বহিঃস্থ বিন্দু C থেকে অঙ্কিত দুটি স্পর্শক বৃত্তকে যথাক্রমে P ও Q বিন্দুতে স্পর্শ করে । বৃত্তের অপর একটি বিন্দু R –তে অঙ্কিত স্পর্শক CP ও CQ কে যথাক্রমে A ও B বিন্দুতে ছেদ করে । যদি CP = 11সেমি. এবং BC = 7 সেমি. হয় , তাহলে BR এর দৈর্ঘ্য নির্ণয় করি ।
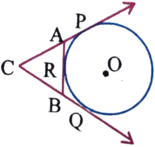
সমাধানঃ বহিঃস্থ বিন্দু C থেকে দুটি স্পর্শক CP ও CQ অঙ্কন করা হয়েছে ।
∴ CP = CQ = 11 সেমি.
আবার , বহিঃস্থ বিন্দু B থেকে দুটি স্পর্শক BQ ও BR অঙ্কন করা হয়েছে ।
∴ BR =BQ
BQ = CQ-BC= 11-7=4 সেমি.
∴ BR = 4 সেমি.( উত্তর)
(V) দুটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 8 সেমি. ও 3 সেমি. এবং তাদের কেন্দ্রদ্বয়ের মধ্যে দূরত্ব 13 সেমি. । বৃত্ত দুটির সরল সাধারন স্পর্শকের দৈর্ঘ্য নির্ণয় কর ।
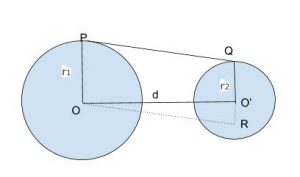
সমাধানঃ বৃত্তদ্বয়ের ব্যাসার্ধের দৈর্ঘ্য যথাক্রমে r1 = 8 সেমি. এবং r2 = 3 সেমি.
বৃত্তদ্বয়ের কেন্দ্রদ্বয়ের মধ্যে দূরত্ব (d) = 13 সেমি.
বৃত্ত দুটির মধ্যে সরল সাধারন স্পর্শকের দৈর্ঘ্য

সরল সাধারন স্পর্শক এর দূরত্ব 12 সেমি. ( উত্তর )
বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.2।Koshe Dekhi 15.2 Class 10|কষে দেখি ১৫.২ ক্লাস ১০