WBBSE Class 9 Math Koshe Dekhi 15.3|ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল কষে দেখি ১৫.৩|Ganit Prakash Class 9 Koshe Dekhi 15.3 (Chapter 15)Solution|West Bengal Board Class 9 Math Book Solution In Bengali|গণিত প্রকাশ নবম শ্রেণি (ক্লাস-৯) সমাধান ।
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
WBBSE Class 9 Math Koshe Dekhi 15.3|ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল কষে দেখি ১৫.৩|Ganit Prakash Class 9 Koshe Dekhi 15.3 (Chapter 15) Solution|West Bengal Board Class 9 Math Book Solution In Bengali|গণিত প্রকাশ নবম শ্রেণি (ক্লাস-৯) সমাধান ।
Koshe Dekhi-15.3 |কষে দেখি -১৫.৩
1. রাতুল একটি সামান্তরিক অঙ্কন করেছে যার ভূমির দৈর্ঘ্য 5 সেমি. এবং উচ্চতা 4 সেমি. । রাতুলের আঁকা সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি ।

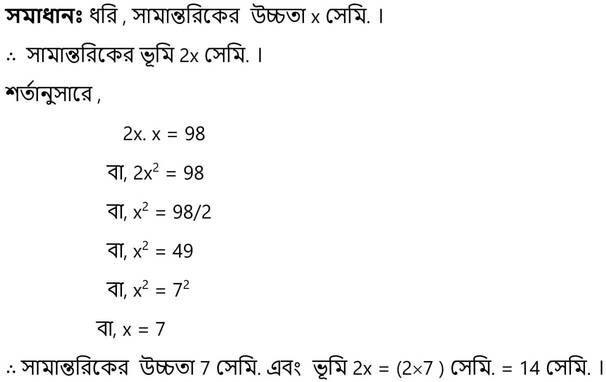
2. একটি সামান্তরিকের ভূমি তার উচ্চতার দ্বিগুন । যদি সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল 98 বর্গ সেমি. হয় ,তাহলে সামান্তরিকের দৈর্ঘ্য ও উচ্চতার পরিমাপ হিসাব করে লিখি ।
3. আমাদের বাড়ির পাশে একটি সামান্তরিক আকারের জমি আছে যার সন্নিহিত বাহুদ্বয়ের দৈর্ঘ্য যথাক্রমে 15 মিটার ও 13 মিটার । যদি এই জমির একটি কর্ণের দৈর্ঘ্য 14 মিটার হয় , তবে হিসাব করে সামান্তরিক আকারের জমির ক্ষেত্রফল লিখি ।
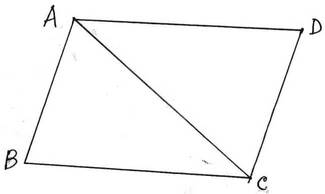
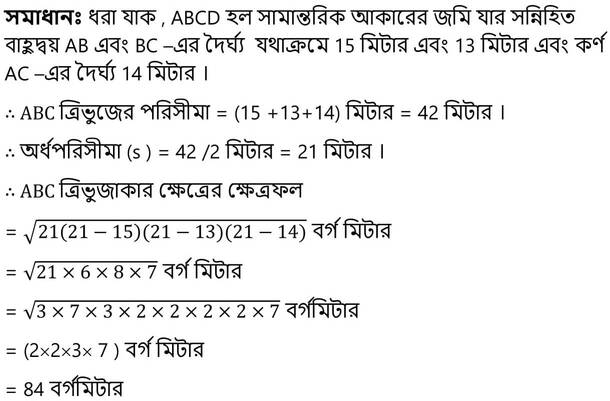
∴ ABCD সামান্তরিকের ক্ষেত্রফল
= 2 ✕ ∆ABC-এর ক্ষেত্রফল [যেহেতু সামান্তরিকের কর্ণ সামান্তরিকটিকে দুটি সর্বসম ত্রিভুজে বিভক্ত করে]
= (2✕ 84 ) বর্গ মিটার
= 168 বর্গ মিটার [উত্তর ]
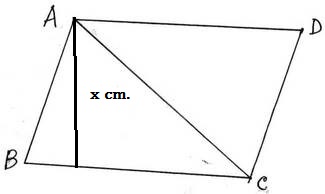
4. পৃথা একটি সামান্তরিক এঁকেছে যার সন্নিহিত বাহুগুলির দৈর্ঘ্য 25 সেমি. ও 15 সেমি. এবং একটি কর্ণের দৈর্ঘ্য 20 সেমি. । হিসাব করে 25 সেমি. বাহুর ওপর সামান্তরিকের উচ্চতা হিসাব করে লিখি ।

= 2☓3☓5☓5 বর্গ সেমি.
= 150 বর্গ সেমি.
ধরি , 25 সেমি. বাহুর (BC) – এর ওপর অঙ্কিত লম্বের দৈর্ঘ্য x সেমি. ।
∴ ½ ☓ BC ☓ x = 150
বা, ½ ☓ 25 ☓ x = 150
বা, 25x = 150☓2
বা, 25x = 300
বা, x = 300/25
বা, x = 12
∴ 25 সেমি. বাহুর ওপর সামান্তরিকের উচ্চতা 12 সেমি. ।
| WBBSE Class 9 Math Koshe Dekhi 15.3|ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল কষে দেখি ১৫.৩|Ganit Prakash Class 9 Koshe Dekhi 15.3(Chapter 15) Solution|West Bengal Board Class 9 Math Book Solution In Bengali|গণিত প্রকাশ নবম শ্রেণি (ক্লাস-৯) সমাধান । |
5. একটি সামান্তরিকের দুটি সন্নিহিত বাহুর দৈর্ঘ্য 15 সেমি. ও 12 সেমি. । ক্ষুদ্রতর বাহুদুটির মধ্যে দূরত্ব 7.5 সেমি. হলে , বৃহত্তর বাহুদুটির মধ্যে দূরত্ব হিসাব করি ।
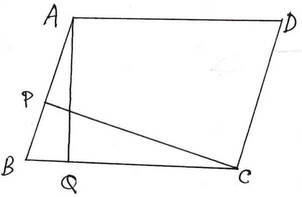

6. একটি রম্বসের কর্ণদ্বয়ের পরিমাপ 15 মিটার ও 20 মিটার হলে ,উহার পরিসীমা ,ক্ষেত্রফল ও উচ্চতা হিসাব করে লিখি ।
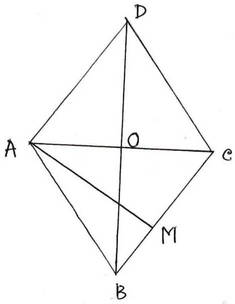

∴ AOB সমকোণী ত্রিভুজ থেকে পাই ,
AB2 = AO2 +BO2
⇒ AB2 = (10)2 +(15/2)2

7. একটি রম্বসের পরিসীমা 400 মিটার এবং সমান্তরাল বাহুদুটির মধ্যে দূরত্ব 22 মিটার হলে , রম্বস আকার ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি ।

8. যদি একটি রম্বসের পরিসীমা 20 সেমি. এবং একটি কর্ণের দৈর্ঘ্য 6 সেমি. হয় , তবে ওই রম্বসের ক্ষেত্রফল হিসাব করে লিখি ।
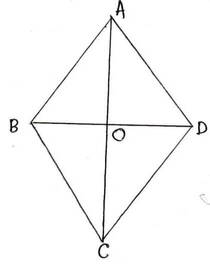

9. একটি ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল 1400 বর্গ ডেকামিটার ।উহার সমান্তরাল বাহুদ্বয়ের মধ্যে লম্ব দূরত্ব 20 ডেকামিটার এবং সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্যের অনুপাত 3:4 হলে , ওই বাহুদ্বয়ের দৈর্ঘ্য হিসাব করে লিখি ।
সমাধানঃ ধরি , ট্রাপিজিয়াম আকার ক্ষেত্রের সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্য যথাক্রমে 3x ডেকামিটার এবং 4x ডেকামিটার ।
∴ ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল = ½ ☓ (সমান্তরাল বাহুদ্বয়ের যোগফল ) ☓ উচ্চতা = {½ ☓ (3x+4x) ☓ 20 } বর্গ ডেকামিটার
প্রশ্নানুসারে ,
½ ☓ (3x+4x) ☓ 20 = 1400
বা, ½ ☓ 7x ☓ 20 = 1400
বা, 140x = 2800
বা, x = 2800 /140
বা, x = 20
∴ সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্য যথাক্রমে 3x = (3☓20) ডেকামিটার = 60 ডেকামিটার এবং 4x = (4☓20 )ডেকামিটার = 80 ডেকামিটার ।
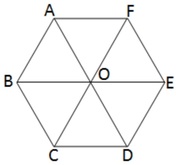
10. 8 সেমি. বাহু বিশিষ্ট সুষম ষড়ভুজাকার ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি ( সংকেতঃ সুষম ষড়ভুজের কর্ণ গুলি আঁকা হলে ছয়টি সর্বসম সমবাহু ত্রিভুজ পাব )

| WBBSE Class 9 Math Koshe Dekhi 15.3|ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল কষে দেখি ১৫.৩|Ganit Prakash Class 9 Koshe Dekhi 15.3(Chapter 15) Solution|West Bengal Board Class 9 Math Book Solution In Bengali|গণিত প্রকাশ নবম শ্রেণি (ক্লাস-৯) সমাধান । |
11. ABCD চতুর্ভুজের AB =5 মিটার ,BC =12 মিটার , CD =14 মিটার ,DA = 15 মিটার এবং ABC = 90 হলে ABCD চতুর্ভুজাকার ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি ।
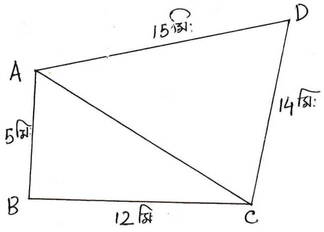
সমাধানঃ ABCD চতুর্ভুজের AC কর্ণ এবং ∠ABC =90°
∴ সমকোণী ত্রিভুজ ABC এর ক্ষেত্রফল = ½ ☓ BC ☓ AB = ½ ☓ 12 ☓ 5 বর্গ মিটার = 30 বর্গমিটার
আবার , সমকোণী ত্রিভুজ ABC থেকে পাই ,
AC2 =AB2 +BC2
বা, AC2 = (5)2 + (12)2
বা, AC2 = 25+144
বা, AC2 = 169
বা, AC2 = (13)2
বা, AC =13
∴ ADC ত্রিভুজের পরিসীমা =(15+14+13) মিটার = 42 মিটার ।
∴ ADC ত্রিভুজের অর্ধ -পরিসীমা (s ) = 42 /2 মিটার = 21 মিটার ।
∴ ADC ত্রিভুজের ক্ষেত্রফল

∴ ABCD চতুর্ভুজের ক্ষেত্রফল = (∆ABC+∆ADC) -এর ক্ষেত্রফল = (30 +84 )বর্গ মিটার = 114 বর্গ মিটার। [উত্তর ]
12. সাহিন ABCD একটি ট্রাপিজিয়াম এঁকেছে ,যার BD কর্ণের দৈর্ঘ্য 11 সেমি. এবং A ও C বিন্দু থেকে BD কর্ণের ওপর দুটি লম্ব এঁকেছে যাদের দৈর্ঘ্য যথাক্রমে 5 সেমি. ও 11 সেমি. ।হিসাব করে ট্রাপিজিয়াম আকার ক্ষেত্র ABCD- এর ক্ষেত্রফল লিখি ।
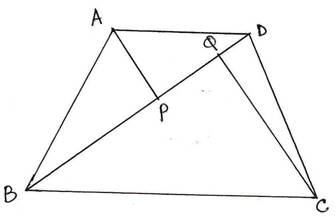
সমাধানঃ ABCD ট্রাপিজিয়ামের BD কর্ণের দৈর্ঘ্য 11 সেমি. ।
ধরি , A ও C বিন্দু থেকে BD কর্ণের অপর অঙ্কিত লম্বের দৈর্ঘ্য যথাক্রমে AP ও BQ এবং AP = 5 সেমি. এবং BQ = 11 সেমি. ।
∴ ABCD ট্রাপিজিয়ামের ক্ষেত্রফল
= ½ ☓(AP+BQ) ☓ BD
= { ½ ☓ (5+11) ☓ 11 } বর্গ সেমি.
= { ½ ☓16 ☓ 11 } বর্গ সেমি.
= 88 বর্গ সেমি.
∴ ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল 88 বর্গ সেমি. ।
13. ABCDE একটি পঞ্চভুজ যার BC বাহুটি AD কর্ণের সমান্তরাল । EP ,BC এর ওপর লম্ব এবং EP ,AD –কে Q বিন্দুতে ছেদ করেছে । BC =7 সেমি. , AD =13 সেমি. ,PE = 9 সেমি. এবং PQ =4/9 PE হলে , ABCDE পঞ্চভুজাকার ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি ।
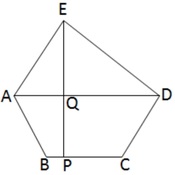
সমাধানঃ ABCDE একটি পঞ্চভুজ যার BC বাহুটি AD কর্ণের সমান্তরাল । EP ,BC এর ওপর লম্ব এবং EP ,AD –কে Q বিন্দুতে ছেদ করেছে ।BC =7 সেমি. , AD =13 সেমি. ,PE = 9 সেমি. এবং PQ =4/9 PE = (4/9 ☓ 9)সেমি. = 4 সেমি. ।
EQ = (PE-PQ) =(9-4 )সেমি. =5 সেমি.
এখন , ABCD ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল = ½ ☓ (AD+BC) ☓ PQ = ½ ☓ (13+7)☓ 4 বর্গ সেমি. =½ ☓ 20 ☓ 4 = 40 বর্গ সেমি.
এখন যেহেতু BC || AD এবং EP ⊥ BC
∴ EQ ⊥ AD
∴ ∆EAD এর ক্ষেত্রফল = ½ ☓ AD ☓ EQ = ( ½ ☓ 13 ☓ 5 ) বর্গ সেমি. = 32.5 বর্গ সেমি.
∴ ABCDE পঞ্চভুজের ক্ষেত্রফল =ABCD ট্রাপিজিয়ামের ক্ষেত্রফল + EAD ত্রিভুজের ক্ষেত্রফল = 40বর্গ সেমি. + 32.5 বর্গ সেমি. =72.5 বর্গ সেমি. [উত্তর ]
14. একটি রম্বসের বাহুর দৈর্ঘ্য ও একটি বর্গ ক্ষেত্রের বাহুর দৈর্ঘ্য সমান এবং বর্গক্ষেত্রটির কর্ণের দৈর্ঘ্য 40√2 সেমি. ।যদি রম্বসের কর্ণদ্বয়ের দৈর্ঘ্যের অনুপাত 3:4 হয় , তাহলে রম্বস আকার ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি ।
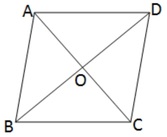
সমাধানঃ ধরি , ABCD একটি রম্বস যার প্রতিটি বাহুর দৈর্ঘ্য a সেমি. ।
∴ বর্গক্ষেত্রের বাহুর দৈর্ঘ্য a সেমি. [যেহেতু , রম্বস ও বর্গক্ষেত্রের বাহুর দৈর্ঘ্য পরস্পর সমান ]
∴ a√2 = 40√2
বা, a = 40
∴ রম্বসের বাহুর দৈর্ঘ্য 40 সেমি. ।
ধরি , রম্বসের কর্ণদ্বয় AC = 3x সেমি. এবং BD = 4x সেমি. । এখন রম্বস ABCD এর কর্ণদ্বয় পরস্পরকে O বিন্দুতে সমকোণে সমদ্বিখন্ডিত করে ।
∴ সমকোণী ত্রিভুজ ABC থেকে পাই ,
AO2 +BO2 = AB2
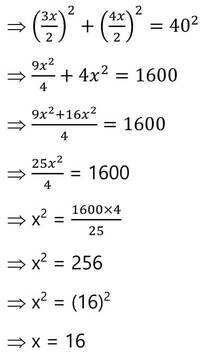
∴ AC কর্ণের দৈর্ঘ্য = 3x সেমি. = (3☓16 )সেমি. = 48 সেমি. এবং BD কর্ণের দৈর্ঘ্য = 4x সেমি. = (4☓ 16 )সেমি. = 64 সেমি. ।
∴ ABCD রম্বসের ক্ষেত্রফল = ½ ☓ 48 ☓ 64 বর্গ সেমি. = 1536 বর্গ সেমি.
∴ রম্বসটির ক্ষেত্রফল 1536 বর্গ সেমি. ।
| WBBSE Class 9 Math Koshe Dekhi 15.3|ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল কষে দেখি ১৫.৩|Ganit Prakash Class 9 Koshe Dekhi 15.3 Solution|West Bengal Board Class 9 Math Book Solution In Bengali|গণিত প্রকাশ নবম শ্রেণি (ক্লাস-৯) সমাধান । |
15. একটি সমদ্বিবাহু ট্রাপিজিয়ামের তির্যক বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য 10 সেমি. এবং সমান্তরাল বাহুদুটির দৈর্ঘ্য যথাক্রমে 5 সেমি. ও 17 সেমি. । ট্রাপিজিয়াম আকার ক্ষেত্রের কর্ণের দৈর্ঘ্য ও ক্ষেত্রফল হিসাব করে লিখি ।
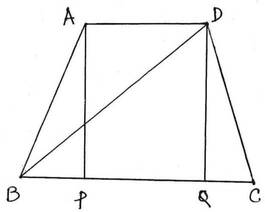
সমাধানঃ ধরি , ABCD সমদ্বিবাহু ট্রাপিজিয়ামের তির্যক বাহুদ্বয় AB = CD =10 সেমি. এবং সমান্তরাল বাহুদুটির দৈর্ঘ্য জথক্রমে AD =5 সেমি. ও BC = 17 সেমি. ।
A ও D বিন্দু থেকে BC বাহুর ওপর যথাক্রমে AP ও DQ লম্ব টানা হল ।
∵ AD ||BC
∴ PQ =AD = 5সেমি.
আবার যেহেতু , AB =CD
সুতরাং BP = CQ = ½ (17 – 5) সেমি. = 6 সেমি.
এখন সমকোণী ত্রিভুজ ABP এর ,
AP2 =AB2 –BP2
বা , AP2 = 102 – 62
বা, AP2 = 100-36
বা, AP2 = 100 -36
বা, AP2 = 64
বা, AP2 = 82
বা, AP =8
∴ ট্রাপিজিয়ামের উচ্চতা 8 সেমি. ।
এখন সমকোণী ত্রিভুজ DBQ এর ,
BQ =BP +PQ = (6+5)সেমি. = 11 সেমি. এবং DQ = AP =8 সেমি. ।
∴ BD2 =BQ2 +DQ2
বা, BD2 = 112+82
বা, BD2 = 121 +64
বা,BD2 = 185
বা, BD = √185
∴ ট্রাপিজিয়ামটির উচ্চতা √185 সেমি. ।
এবং ABCD ট্রাপিজিয়ামের ক্ষেত্রফল = {½☓ ( 17 +5 ) ☓ 8} বর্গ সেমি. = 88 বর্গ সেমি.
∴ ABCD ট্রাপিজিয়ামের ক্ষেত্রফল 88 বর্গসেমি এবং উচ্চতা √185 সেমি. ।
16. একটি ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্য 19 সেমি. ও 9 সেমি. এবং তির্যক বাহুদ্বয়ের দৈর্ঘ্য 8 সেমি. ও 6 সেমি. । ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল হিসাব করি ।
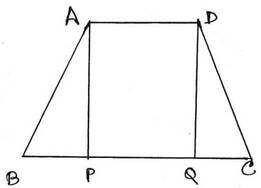
সমাধানঃ ধরি ,ABCD ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্য BC = 19 সেমি. ও AD = 9 সেমি. এবং তির্যক বাহুদ্বয়ের দৈর্ঘ্য AB =8 সেমি. এবং CD = 6 সেমি. ।
A ও D বিন্দু থেকে BC বাহুর ওপর যথাক্রমে AP ও DQ লম্ব টানা হল ।
∵ AD || BC
∴ PQ =AD = 9 সেমি.
∴ BP =BC –(PQ+CQ) = 19 –(9+CQ) =10-CQ
এখন , সমকোণী ত্রিভুজ ABP –এর ,
BP2 = AB2 –BP2
বা, AP2 = 64 – BP2 —-(i)
আবার , সমকোণী ত্রিভুজ DCQ এর ,
DQ2 =DC2 –CQ2
বা, DQ2 = 62 – CQ2
বা, DQ2 = 36 – CQ2 —-(ii)
আবার , AP =DQ
∴ AP2 =DQ2
বা, 64 – BP2 = 36 – CQ2
বা, 64 –(10-CQ)2 = 36 –CQ2
বা, 64 –(100-20CQ +CQ2) = 36 – CQ2
বা, 64 -100 +20CQ –CQ2 = 36 –CQ2
বা, 20CQ = 36-64 +100
বা, CQ = 72/20
বা, CQ = 18/5

∴ ট্রাপিজিয়ামটির উচ্চতা AP =DQ = 4.8 সেমি. ।
∴ ট্রাপিজিয়ামটির ক্ষেত্রফল = ½ ☓ (19+9 ) ☓ 4.8 বর্গ সেমি. = ½ ☓ 28 ☓ 4.8 বর্গ সেমি. = 67.2 বর্গ সেমি. । [উত্তর ]
| WBBSE Class 9 Math Koshe Dekhi 15.3|ত্রিভুজ ও চতুর্ভুজের পরিসীমা ও ক্ষেত্রফল কষে দেখি ১৫.৩|Ganit Prakash Class 9 Koshe Dekhi 15.3 Solution|West Bengal Board Class 9 Math Book Solution In Bengali|গণিত প্রকাশ নবম শ্রেণি (ক্লাস-৯) সমাধান । |
17. বহু বিকল্পীয় প্রশ্ন (M.C.Q)
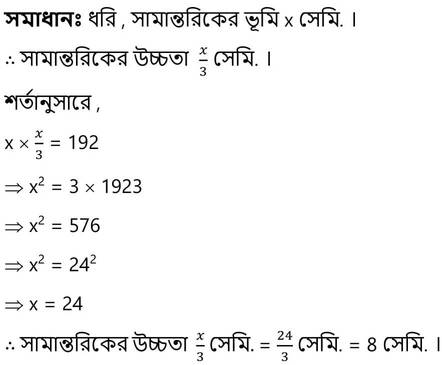
(i) একটি সামান্তরিকের উচ্চতা ভূমির একতৃতীয়াংশ । সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল 192 বর্গ সেমি. হলে ,সামান্তরিকের উচ্চতা
(a) 4 সেমি
(b) 8 সেমি.
(c ) 16 সেমি.
(d ) 24 সেমি.
Ans: (b) 8 সেমি.
(ii) একটি রম্বসের একটি বাহুর দৈর্ঘ্য 6 সেমি. এবং একটি কোণের পরিমাপ 60° হলে , রম্বস আকার ক্ষেত্রের ক্ষেত্রফল
(a) 9√3 বর্গ সেমি.
(b) 18√3 বর্গ সেমি.
(c ) 36√3 বর্গ সেমি.
(d ) 6√3 বর্গ সেমি.
Ans:(b) 18√3 বর্গ সেমি.
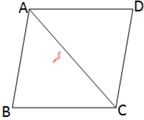
সমাধানঃ ABCD রম্বসের বাহুর দৈর্ঘ্য 6 সেমি. এবং ∠ABC =60° । AC কর্ণ যোগ করে পাই , ∠BAC =∠BCA = (180°-60°) /2 = 60°
∵ AC কর্ণ ABCD রম্বসকে দুটি 6 সেমি. বাহু বিশিষ্ট সমবাহু ত্রিভুজে বিভক্ত করেছে ।
(iii) একটি রম্বসের একটি কর্ণের দৈর্ঘ্য অপর কর্ণটির দৈর্ঘ্যের তিনগুন । যদি রম্বস আকার ক্ষেত্রের ক্ষেত্রফল 96 বর্গ সেমি. হয় তাহলে বড় কর্ণটির দৈর্ঘ্য
(a ) 8 সেমি.
(b) 12 সেমি.
(c) 16 সেমি.
(d) 24 সেমি.
Ans: (d) 24 সেমি.
সমাধানঃ ধরি , একটি কর্ণের দৈর্ঘ্য x সেমি.
∴ অপর কর্ণের দৈর্ঘ্য হবে 3x সেমি. ।
প্রশ্নানুসারে ,
½ ☓ x ☓ 3x = 96
বা, 3x2 = 96 ☓ 2
বা, 3x2 = 192
বা, x2 = 192/3
বা, x2 = 64
বা, x2 = 82
বা, x = 8
∴ বড় কর্ণটির দৈর্ঘ্য 3x সেমি. = (3☓8) সেমি. = 24 সেমি. ।
(iv) একটি রম্বস ও একটি বর্গক্ষেত্র একই ভূমির অপর অবস্থিত । বর্গক্ষেত্রের ক্ষেত্রফল x2 বর্গ একক এবং রম্বস আকার ক্ষেত্রের ক্ষেত্রফল y বর্গ একক হলে ,
(a) y > x2
(b) y < x2
(c ) y =x2
Ans: (b) y < x2
সমাধানঃ বর্গক্ষেত্রের ক্ষেত্রফল x2 বর্গ একক ।
∴ বর্গক্ষেত্রের প্রতিটি বাহুর দৈর্ঘ্য x একক ।
∴ রম্বসের প্রতিটি বাহুর দৈর্ঘ্য x একক ।
ধরি , রম্বসের উচ্চতা h একক
∴ রম্বসের ক্ষেত্রফল xh বর্গ একক ।
∴ y = xh
স্পষ্টতই , h < x [∵ BFG সমকোণী ত্রিভুজের উচ্চতা (FG) < অতিভুজ (BF) ]
∴ hx < x2
∴ y < x2
(v) একটি ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল 162 বর্গ সেমি. এবং উচ্চতা 6 সেমি. । ট্রাপিজিয়ামটির একটি সমান্তরাল বাহুর দৈর্ঘ্য 23 সেমি. হলে , অপর সমান্তরাল বাহুর দৈর্ঘ্য
(a) 29 সেমি.
(b) 31 সেমি.
(c ) 32 সেমি.
(d) 33 সেমি.
Ans: (b) 31 সেমি.

18. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ
(i) ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল 96 বর্গ সেমি. ও BD কর্ণের দৈর্ঘ্য 12 সেমি. । A বিন্দু থেকে BD কর্ণের ওপর লম্বের দৈর্ঘ্য কত ?
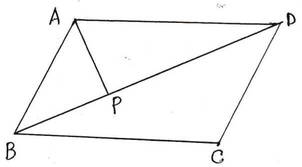
সমাধানঃ ধরা যাক , ABCD সামান্তরিকের A বিন্দু থেকে BD কর্ণের ওপর AP লম্ব টানা হল ।
সামান্তরিকের কর্ণ সামান্তরিককে দুটি সমান ক্ষেত্রফল বিশিষ্ট ত্রিভুজে বিভক্ত করে ।
∴ ABD এর ক্ষেত্রফল = ½ ☓ 96 বর্গ সেমি. = 48 বর্গ সেমি.
আবার ABD এর ক্ষেত্রফল = ½ ☓ BD ☓ AP = ½ ☓ 12☓ AP = 6AP
∴ 6AP = 48
বা, AP = 48/6
বা, AP = 8
∴ A বিন্দু থেকে BD কর্ণের ওপর লম্বের দৈর্ঘ্য 8 সেমি. ।
(ii) একটি সামান্তরিকের সন্নিহিত বাহুদ্বয়ের দৈর্ঘ্য 5 সেমি. এবং 3 সেমি. । বৃহত্তর বাহুদ্বয়ের মধ্যে দূরত্ব 2 সেমি. হলে ক্ষুদ্রতর বাহুদ্বয়ের মধ্যে দূরত্ব কত ?

(iii) একটি রম্বসের উচ্চতা 4 সেমি. এবং বাহুর দৈর্ঘ্য 5 সেমি.। রম্বস আকার ক্ষেত্রের ক্ষেত্রফল কত ?
সমাধানঃ রম্বসের ক্ষেত্রফল = (ভূমি ☓ উচ্চতা ) =(5☓4) বর্গ সেমি. = 20 বর্গ সেমি.
(iv) একটি সমদ্বিবাহু ট্রাপিজিয়ামের যেকোনো সমান্তরাল বাহু সংলগ্ন একটি কোণ 45° ;ট্রাপিজিয়ামের তির্যক বাহুর দৈর্ঘ্য 62 সেমি. হলে , সমান্তরাল বাহুদ্বয়ের মধ্যে দূরত্ব কত ?
সমাধানঃ ধরি , ABCD একটি সমদ্বিবাহু ট্রাপিজিয়াম যার AD ||BC এবং সমান্তরাল বাহু সংলগ্ন একটি কোণ ∠ABC =45° । ধরি , ট্রাপিজিয়ামের তির্যক বাহু AB এর দৈর্ঘ্য 62 সেমি. এবং A বিন্দু থেকে BC -এর ওপর অঙ্কিত লম্ব AP = aসেমি.
∆ABP -এর ∠ABC =45° ,∠APB =90°
∴ ∠BAP = 180° -(90°+45°) =45°
∴ ABP একটি সমকোণী সমদ্বিবাহু ত্রিভুজ যার AP =BP
AP2 +BP2 = AB2
বা, a2+a2 = 622
বা, 2a2 = 62 ✕ 62
বা, a2 = (62 ✕ 62 )/2
বা, a = 31√2
∴ সমান্তরাল বাহুদ্বয়ের মধ্যে দূরত্ব 31√2 সেমি. ।
(v) ABCD সামান্তরিকের AB =4সেমি. , BC = 6 সেমি. এবং ABC = 30º হলে ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল কত ?

Very helpful for tutors and students
Very good 😊