WBBSE Class 9 Math Koshe Dekhi 20|ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল কষে দেখি -20।গণিত প্রকাশ নবম শ্রেণি (ক্লাস ৯)সমাধান ।Ganit Prakash Class 9 Koshe Dekhi 20 Solution|West Bengal Board Class 9 Math Book Solution In Bengali.
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।
গণিত প্রকাশ দশম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।
WBBSE Class 9 Math Koshe Dekhi 20|ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল কষে দেখি -20
কষে দেখি 20
1. নীচের শীর্ষবিন্দু বিশিষ্ট ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল প্রতিক্ষেত্রে নির্ণয় করিঃ
(i) (2,-2) ,(4,2) এবং (-1,3)
সমাধানঃ (2,-2) ,(4,2) এবং (-1,3) শীর্ষবিন্দুবিশিষ্ট ত্রিভুজের ক্ষেত্রফল –
= ½ |x1(y2-y3) +x2(y3-y1)+x3(y1-y2)|বর্গএকক
= ½ |2(2-3)+4{3-(-2)}+(-1)(-2-2)}| বর্গএকক [ এক্ষেত্রে , (x1,y1) = (2,-2) , (x2,y2) = (4,2) এবং (x3,y3) = (-1,3) ]
= ½ |{2✕(-1)}+(4✕5) + {(-1)✕(-4)} | বর্গএকক
= ½ |(-2+20+4)| বর্গএকক
= ½ ✕ 22 বর্গএকক
= 11 বর্গএকক [উত্তর]
WBBSE Class 9 Math Koshe Dekhi 20|ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল কষে দেখি -20
(ii) (8,9) ,(2,6) এবং (9,2)
সমাধানঃ (8,9) ,(2,6) এবং (9,2) স্থানাঙ্কবিশিষ্ট ত্রিভুজের ক্ষেত্রফল
= ½ |x1(y2-y3) +x2(y3-y1)+x3(y1-y2)| বর্গএকক
= ½ |8(6-2)+2(2-9)+9(9-6)| বর্গএকক [এক্ষেত্রে ,(x1,y1) = (8,9),(x2,y2) =(2,6) এবং (x3,y3)= (9,2) ]
= ½ |(32-14+27| বর্গএকক
= ½ ✕ 45 বর্গএকক
= 22 ½ বর্গএকক [উত্তর]
WBBSE Class 9 Math Koshe Dekhi 20|ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল কষে দেখি -20
(iii) (1,2) ,(3,0) এবং মূলবিন্দু
সমাধানঃ প্রদত্ত বিন্দুগুলি হল – (1,2) ,(3,0) এবং মূলবিন্দু
অর্থাৎ (1,2) ,(3,0) এবং (0,0) স্থানাঙ্কবিশিষ্ট ত্রিভুজের ক্ষেত্রফল
= ½ |x1(y2-y3) +x2(y3-y1)+x3(y1-y2)| বর্গএকক
= ½ |1(0-0) +3(0-2)+0(2-0)|বর্গএকক [ এক্ষেত্রে , (x1,y1) = (1,2) , (x2,y2)= (3,0) এবং (x3,y3) = (0,0) ]
= ½ |-6| বর্গএকক
= ½ ✕ 6 বর্গএকক
= 3 বর্গএকক [উত্তর]
WBBSE Class 9 Math Koshe Dekhi 20|ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল কষে দেখি -20
2. প্রমাণ করি যে, (3,-2) , (-5,4) এবং (-1,1) বিন্দু তিনটি সমরেখ ।
সমাধানঃ (3,-2) , (-5,4) এবং (-1,1) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল
= ½ |x1(y2-y3) +x2(y3-y1)+x3(y1-y2)| বর্গএকক
= ½ |3(4-1)+(-5){1-(-2)}+(-1)(-2-4)| বর্গএকক [এক্ষেত্রে , (x1,y1) = (3,-2),(x2,y2) = (-5,4) এবং (x3,y3) = (-1,1) ]
= ½ |(3✕3) + (-5)✕(3) +{(-1)✕(-6)}| বর্গএকক
= ½ |9 – 15 +6| বর্গএকক
= 0
যেহেতু , (3,-2) , (-5,4) এবং (-1,1) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল 0
∴ বিন্দু তিনটি সমরেখ [প্রমাণিত] ।
WBBSE Class 9 Math Koshe Dekhi 20|ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল কষে দেখি -20
3. K –এর মান কত হলে , (1,-1) ,(2,-1) এবং (K ,-1)বিন্দু তিনটি সমরেখ ।
সমাধানঃ (1,-1) ,(2,-1) এবং (K ,-1) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজটির ক্ষেত্রফল
∴ ½ |x1(y2-y3) +x2(y3-y1)+x3(y1-y2)| বর্গএকক
= ½ |1{-1-(-1)} + 2{-1-(-1)} + (K){-1-(-1)}| বর্গএকক [ এক্ষেত্রে (x1,y1) = (1,-1) ,(x2,y2) = (2,-1) এবং (x3,y3) = (K,-1) ]
= ½ |1(-1+1) +2(-1+1)+ K(-1+1)| বর্গএকক
= 0
∴ K -এর যেকোনো বাস্তব মানের জন্য প্রদত্ত বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল শূন্য ।
∴ K –এর যেকোনো বাস্তব মানের জন্য প্রদত্ত বিন্দু তিনটি সমরেখ হবে ।
WBBSE Class 9 Math Koshe Dekhi 20|ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল কষে দেখি -20
4. প্রমাণ করি যে , (1,2) এবং (-2,-4) বিন্দুদ্বয়ের সংযোজক সরলরেখা মূলবিন্দুগামী ।
সমাধানঃ (1,2 ), (-2 ,-4) এবং মূলবিন্দু (0,0) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল
= ½ |x1(y2-y3) +x2(y3-y1)+x3(y1-y2)| বর্গএকক
= ½ | 1(-4-0) + (-2)(0 – 2) + 0{2-(-4)}| বর্গএকক [এক্ষেত্রে ,(x1,y1) =(1,2), (x2,y2) = (-2,-4) এবং (x3,y3) = (0,0) ]
= ½ | (-4 +4 )| বর্গএকক
= 0
যেহেতু , (1,2 ), (-2 ,-4) এবং মূলবিন্দু (0,0) দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল 0 ।
∴ (1,2 ), (-2 ,-4) এবং (0,0) বিন্দুগুলি সমরেখ ।
∴ (1,2) এবং (-2,-4) বিন্দুদ্বয়ের সংযোজক সরলরেখা মূলবিন্দুগামী [প্রমাণিত ]।
WBBSE Class 9 Math Koshe Dekhi 20|ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল কষে দেখি -20
5. প্রমাণ করি যে , (2,1) এবং (6,5) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশের মধ্যবিন্দু (-4,-5) ও (9,8 ) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশের উপর অবস্থিত ।
সমাধানঃ (2,1) এবং (6,5) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশের মধ্যবিন্দুর স্থানাঙ্ক (2+6 /2 , 1+5 /2 ) = (4, 3)
∴ (-4,-5) , (9,8 ) এবং (4,3) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল
= ½ |x1(y2-y3) +x2(y3-y1)+x3(y1-y2)|
= ½ |-4 (8-3) + 9{3-(-5)} + 4 (-5 – 8)| বর্গএকক [এক্ষেত্রে , (x1,y1)=(-4,-5) , (x2,y2) = (9,8 ) এবং (x3,y3) = (4,3) ]
= ½ | (-4)(5) + 9(8) + 4(-13)| বর্গএকক
= ½ | -20 +72 -52| বর্গএকক
= ½ |-72 +72| বর্গএকক
= ½ |0| বর্গএকক
= 0
∴ (-4,-5) , (9,8 ) এবং (4,3) বিন্দু তিনটি সমরেখ ।
∴ (2,1) এবং (6,5) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশের মধ্যবিন্দু (-4,-5) ও (9,8 ) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশের উপর অবস্থিত ।
WBBSE Class 9 Math Koshe Dekhi 20|ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল কষে দেখি -20
6. নীচের প্রতিক্ষেত্রে প্রদত্ত বিন্দু চারটির সংযোগে গঠিত চতুর্ভুজাকার ক্ষেত্রের ক্ষেত্রফল নির্ণয় করিঃ
(i) (1,1) ,(3,4),(5,-2) ,(4,-7)
সমাধানঃ
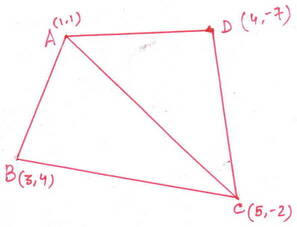
ধরি , ABCD চতুর্ভুজের A,B ,C এবং D বিন্দুগুলির স্থানাঙ্ক যথাক্রমে (1,1) ,(3,4),(5,-2) এবং (4,-7) ।
এখন , AC কর্ণ টানা হল যার ফলে চতুর্ভুজটি দুটি ত্রিভুজ ∆ABC এবং ∆ACD –তে বিভক্ত হল ।
ABC ত্রিভুজের ক্ষেত্রফল –
= ½ |x1(y2-y3) +x2(y3-y1)+x3(y1-y2)| বর্গএকক
= ½ |1{4-(-2)} + 3(-2-1) + 5(1-4)| বর্গএকক [এক্ষেত্রে , (x1,y1) = (1,1) ,(x2,y2) = (3,4) ,(x3,y3) = (5,-2)]
= ½ |(6 – 9 -15)|বর্গএকক
= ½ |-18| বর্গএকক
= (½ ✕18) বর্গএকক
= 9 বর্গএকক
ACD ত্রিভুজের ক্ষত্রফল –
= ½ |x1(y2-y3) +x2(y3-y1)+x3(y1-y2)| বর্গএকক
= ½ |1{-2-(-7)} + 5(-7-1) + 4{1-(-2)}| বর্গএকক
[এক্ষেত্রে , (x1,y1) = (1,1) ,(x2,y2) = (5,-2) ,(x3,y3) = (4,-7)]
= ½ |(-2+7) + 5(-8) +4(3)| বর্গএকক
= ½ |(5 -40 +12)| বর্গএকক
= ½ |-23| বর্গএকক
= ½ ✕ 23 বর্গএকক
= 23/2 বর্গএকক
∴ ABCD চতুর্ভুজের ক্ষেত্রফল
= ∆ABC –এর ক্ষেত্রফল + ∆ACD এর ক্ষেত্রফল
= (9+23/2) বর্গএকক
= (18+23)/2 বর্গএকক
= 41/2 বর্গএকক

WBBSE Class 9 Math Koshe Dekhi 20|ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল কষে দেখি -20
(ii) (1,4) ,(-2,1) ,(2,-3) ,(3,3)
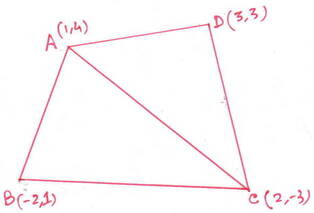
সমাধানঃ ধরি , ABCD চতুর্ভুজের A,B ,C এবং D বিন্দুগুলির স্থানাঙ্ক যথাক্রমে (1,4) ,(-2,1) ,(2,-3) এবং (3,3) ।
এখন , AC কর্ণ টানা হল যার ফলে চতুর্ভুজটি দুটি ত্রিভুজ ∆ABC এবং ∆ACD –তে বিভক্ত হল ।
∆ABC ত্রিভুজের ক্ষেত্রফল –
= ½ |x1(y2-y3) +x2(y3-y1)+x3(y1-y2)| বর্গএকক
= ½ |1{1-(-3)} + (-2)(-3-4) + 2(4-1)| বর্গএকক
[এক্ষেত্রে , (x1,y1) = (1,4) ,(x2,y2) = (-2,1) ,(x3,y3) = (2,-3)]
= ½ |(4 +14 +6)|বর্গএকক
= ½ |24| বর্গএকক
= 12 বর্গএকক
∆ACD ত্রিভুজের ক্ষত্রফল –
= ½ |x1(y2-y3) +x2(y3-y1)+x3(y1-y2)| বর্গএকক
= ½ |1(-3-3) + 2(3-4) + 3{4-(-3)}| বর্গএকক
[এক্ষেত্রে , (x1,y1) = (1,4) ,(x2,y2) = (2,-3) ,(x3,y3) = (3,3)]
= ½ |(-6 -2+21)| বর্গএকক
= ½ |13| বর্গএকক
= ½ ✕13 বর্গএকক
= 13/2 বর্গএকক
∴ ABCD চতুর্ভুজের ক্ষেত্রফল
= ∆ABC –এর ক্ষেত্রফল + ∆ACD এর ক্ষেত্রফল

WBBSE Class 9 Math Koshe Dekhi 20|ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল কষে দেখি -20
7. A,B,C বিন্দু তিনটির স্থানাঙ্ক যথাক্রমে (3,4) (-4,3) এবং (8,-6) ; ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল নির্ণয় করি এবং A বিন্দু থেকে BC বাহুর উপর লম্বের দৈর্ঘ্য নির্ণয় করি ।
সমাধানঃ
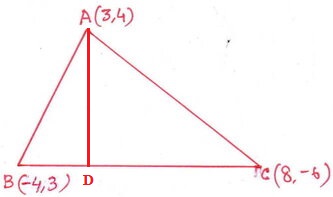
ABC ত্রিভুজের ক্ষেত্রফল –
= ½ |x1(y2-y3) +x2(y3-y1)+x3(y1-y2)| বর্গএকক
= ½ |3{3-(-6)}+ (-4) (-6-4) +8 (4-3)| বর্গএকক
= ½ |3(3+6) + 40 +8|
= ½ |(27+40+8)|
= ½ |75| বর্গএকক
= 37 ½ বর্গএকক
= 37.5 বর্গএকক
এখন , A বিন্দু থেকে BC বাহুর উপর AD লম্ব টানা হল ।
ABC-ত্রিভুজের BC বাহুর দৈর্ঘ্য –

∴ ∆ABC –এর ক্ষেত্রফল = ½ ☓ ভূমি ☓ উচ্চতা = ½ ☓ BC ☓AD = ½ ☓ 15☓BC
∴ ½ ☓ 15 ☓ BC = 37.5
বা, BC = 37.5 ☓ 2 /15
বা, BC = 75/15
বা, BC = 5
∴ ABC –এর A বিন্দু থেকে বিপরীত বাহু BC-এর উপর লম্বের দৈর্ঘ্য 5 একক ।
WBBSE Class 9 Math Koshe Dekhi 20|ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল কষে দেখি -20
8. ABC ত্রিভুজের A বিন্দুর স্থানাঙ্ক (2,5) এবং ত্রিভুজটির ভরকেন্দ্রের স্থানাঙ্ক (-2,1) হলে , BC বাহুর মধ্যবিন্দুর স্থানাঙ্ক নির্ণয় করি ।
সমাধানঃ
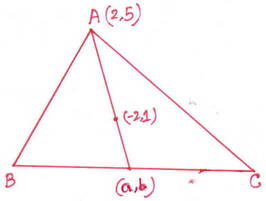
ধরি , BC বাহুর মধ্যবিন্দুর স্থানাঙ্ক (a,b ) । ABC ত্রিভুজের A বিন্দুর স্থানাঙ্ক (2,5) এবং ত্রিভুজটির ভরকেন্দ্রের স্থানাঙ্ক (-2,1) ।
আমরা জানি , কোনো ত্রিভুজের ভরকেন্দ্র ওই ত্রিভুজের মধ্যমাকে 2:1 অনুপাতে বিভক্ত করে ।

বা, 2a +2 = -6
বা, 2a = -6-2
বা, 2a = – 8
বা , a = -8 /2
বা, a = -4
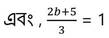
বা, 2b+5 = 3
বা, 2b= 3-5
বা, 2b = -2
বা , b = -2 /2
বা, b = -1
∴মধ্যবিন্দুর স্থানাঙ্ক (-4,-1) ।
WBBSE Class 9 Math Koshe Dekhi 20|ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল কষে দেখি -20
9. একটি ত্রিভুজের তিনটি শীর্ষবিন্দুর স্থানাঙ্ক (4,-3) ,(-5,2) এবং (x,y) ; যদি ত্রিভুজটির ভরকেন্দ্র মূলবিন্দু হয় , তাহলে x ও y এর মান নির্ণয় করি ।
সমাধানঃ ত্রিভুজের তিনটি শীর্ষ বিন্দুর স্থানাঙ্ক (4,-3) ,(-5,2) এবং (x,y) ।

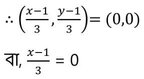
বা, x-1 = 0
বা, x = 1
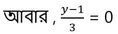
বা, y-1 = 0
বা, y =1
∴ x এর মান 1 এবং y –এর মান 1 ।
WBBSE Class 9 Math Koshe Dekhi 20|ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল কষে দেখি -20
10. A(-1,5) ,B( 3,1) এবং C ( 5,7) ত্রিভুজ ABC –এর শীর্ষবিন্দু । D,E,F যথাক্রমে BC ,CA এবং AB বাহুর মধ্যবিন্দু । DEF ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল নির্ণয় করি এবং দেখাই যে ∆ABC = ∆4 DEF
সমাধানঃ
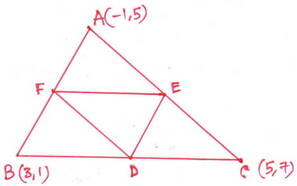
A(-1,5) ,B( 3,1) এবং C ( 5,7) ত্রিভুজ ABC –এর শীর্ষবিন্দু ।
BC বাহুর মধ্যবিন্দু D ।
∴ D বিন্দুর স্থানাঙ্ক = (3+5/2 , 1+7/2) = (8/2 , 8/2) = (4,4)
E , CA বাহুর মধ্যবিন্দু
∴ E বিন্দুর স্থানাঙ্ক = (5-1/2 , 7+5/2) = (4/2 , 12/2) = (2,6)
এবং , F , AB বাহুর মধ্যবিন্দু
∴ F বিন্দুর স্থানাঙ্ক = (-1+3/2 , 5+1/2) = (2/2, 6/2) = (1,3)
ABC ত্রিভুজের ক্ষেত্রফল –
= ½ |x1(y2-y3) +x2(y3-y1)+x3(y1-y2)| বর্গএকক
= ½ |-1(1-7)+3(7-5)+5(5-1)| বর্গএকক [এক্ষেত্রে , (x1,y1) = (-1,5) , (x2,y2) = (3,1) এবং (x3,y3)= (5,7) ]
= ½ |(6 +6 +20)| বর্গএকক
= ½ ✕ 32 বর্গএকক
= 16 বর্গএকক
DEF ত্রিভুজের ক্ষেত্রফল –
= ½ |x1(y2-y3) +x2(y3-y1)+x3(y1-y2)| বর্গএকক
= ½ | 4(6-3) + 2(3-4) + 1(4-6)| বর্গএকক [এক্ষেত্রে , (x1,y1) = (4,4) ,(x2 ,y2) = (2,6) এবং (x3,y3) = (1,3) ]
= ½ | (12 – 2 -2)|বর্গএকক
= ½ ✕ 8 বর্গএকক
= 4 বর্গএকক
∴ ABC এর ক্ষেত্রফল =4 ✕ DEF এর ক্ষেত্রফল [প্রমাণিত]
WBBSE Class 9 Math Koshe Dekhi 20|ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল কষে দেখি -20
11. বহুবিকল্পীয় প্রশ্নঃ
(i) (0,4) , (0,0) এবং (-6,0) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(a) 24 বর্গএকক
(b) 12 বর্গএকক
(c ) 6 বর্গএকক
(d) 8 বর্গএকক
Ans: (b) 12 বর্গএকক
সমাধানঃ
(0,4) , (0,0) এবং (-6,0) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল –
= ½ |0 (0-0) + 0(0 – 4) + (-6) {0 –(-4)}|বর্গএকক
= 1/2 |24| বর্গএকক
= (½ ☓ 24) বর্গএকক
= 12 বর্গএকক
WBBSE Class 9 Math Koshe Dekhi 20|ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল কষে দেখি -20
(ii) (7,-5) ,(-2, 5) এবং (4,6) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ভরকেন্দ্রের স্থানাঙ্ক
(a) (3,-2)
(b) (2,3)
(c ) (3,2)
(d) (2,-3)
Ans: (c ) (3,2)
সমাধানঃ (7,-5) ,(-2, 5) এবং (4,6) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ভরকেন্দ্রের স্থানাঙ্ক –
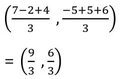
= (3,2)
(iii) ABC সমকোণী ত্রিভুজের ABC =90 ° ; A ও C বিন্দুর স্থানাঙ্ক যথাক্রমে (0,4) এবং (3,0) হলে , ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(a) 12 বর্গএকক
(b) 6 বর্গএকক
(c ) 24 বর্গএকক
(d) 8 বর্গএকক
Ans: (b) 6 বর্গএকক
সমাধানঃ ABC সমকোণী ত্রিভুজের ABC =90 ° ; A ও C বিন্দুর স্থানাঙ্ক যথাক্রমে (0,4) এবং (3,0) হলে , B বিন্দুর স্থানাঙ্ক হবে (0,0) ।
∴ ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল –
= ½ |0 ( 0-0) + 0(0-4) + 3(4-0)| বর্গএকক
= ½ (12) বর্গএকক
= 6 বর্গএকক
(iv) (0,0) ,( 4,-3) এবং (x,y) বিন্দু তিনটি সমরেখ হলে
(a) x=8,y=-6
(b) x =8,y = 6
(c ) x =4,y = -6
(d) x = -8,y = -6
Ans: (a) x = 8,y = -6
সমাধানঃ (0,0) ,( 4,-3) এবং (x,y) বিন্দু তিনটি সমরেখ হলে বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল শূন্য হবে ।
∴ ½ | 0 (-3-y) +4(y-0) + x(0+3) | = 0
বা, ½ | (4y+3x)| = 0
বা, 4y+3x = 0 —(i)
এখন, y = -6 এবং x = 8 (i) নং সমীকরণকে সিদ্ধ করে ।
∴ y = -6 এবং x = 8
(v) ত্রিভুজ ABC এর A শীর্ষবিন্দুর স্থানাঙ্ক (7,-4) এবং ত্রিভুজটির ভরকেন্দ্রের স্থানাঙ্ক (1,2) হলে , BC বাহুর মধ্যবিন্দুর স্থানাঙ্ক
(a) (-2,-5)
(b ) (-2 ,5)
(c ) (2,-5)
(d) (5 ,-2)
Ans: (b ) (-2 ,5)
সমাধানঃ ত্রিভুজ ABC এর A শীর্ষবিন্দুর স্থানাঙ্ক (7,-4)
ধরি , BC বাহুর মধ্যবিন্দুর স্থানাঙ্ক (x ,y)
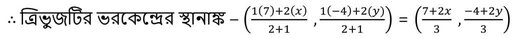
[যেহেতু , ভরকেন্দ্র ত্রিভুজের মধ্যমাকে 2:1 অনুপাতে বিভক্ত করে ]
শর্তানুসারে ,
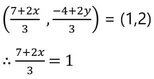
বা, 7+2x = 3
বা, 2x = 3-7
বা, 2x = -4
বা, x = -4/2
বা, x = -2
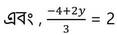
বা, -4 +2y = 6
বা, 2y = 6+4
বা, 2y = 10
বা, y = 10/2
বা, y = 5
∴ BC বাহুর মধ্যবিন্দুর স্থানাঙ্ক (-2,5) ।
WBBSE Class 9 Math Koshe Dekhi 20|ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল কষে দেখি -20
12. সংক্ষিপ্ত উত্তরধর্মী প্রশ্নঃ
(i) ABC ত্রিভুজের বাহুগুলির মধ্যবিন্দুর স্থানাঙ্ক (0,1) , (1,1) এবং (1,0) ; ত্রিভুজের ভরকেন্দ্রের স্থানাঙ্ক নির্ণয় করি ।
সমাধানঃ
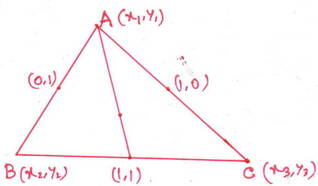
ধরা যাক , ABC ত্রিভুজের A ,B এবং C শীর্ষবিন্দুগুলির স্থানাঙ্ক যথাক্রমে (x1,y1) ,(x2,y2 ) এবং (x3,y3) ।
ABC ত্রিভুজের AB ,BC এবং CA বাহুর মধ্যবিন্দুর স্থানাঙ্ক যথাক্রমে (0,1) , (1,1) এবং (1,0)
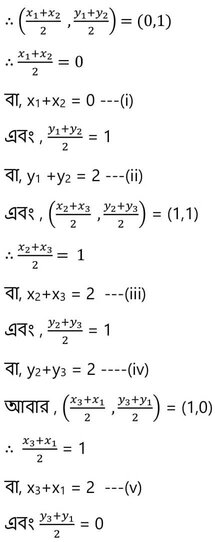
বা, y3+y1 = 0 —(vi)
এখন , (i) ,(iii) এবং (v) নং সমীকরণ যোগ করে পাই ,
x1+x2 +x2+x3+x3+x1 = 4
বা, 2(x1+x2+x3) = 4
বা, x1+x2+x3 = 4/2
বা, x1+x2+x3= 2 — (vii)
(ii) , (iv) এবং (vi) নং সমীকরণ যোগ করে পাই ,
y1+y2 +y2+y3+y3+y1 = 4
বা, 2 (y1+y2+y3) = 4
বা, y1+y2+y3 = 2 —-(viii)
(vii) নং সমীকরণ থেকে (iii) নং সমীকরণ বিয়োগ করে পাই ,
x1+x2+x3 – x2-x3 = 2-2
বা, x1 = 0
আবার , (viii) নং সমীকরণ থেকে (iv) নং সমীকরণ বিয়োগ করে পাই ,
y1+y2+y3 –y2 –y3 = 2- 2
বা, y1 = 0
∴ A-বিন্দুর স্থানাঙ্ক (0,0)
আবার , BC বাহুর মধ্যবিন্দুর স্থানাঙ্ক (1,1) ।
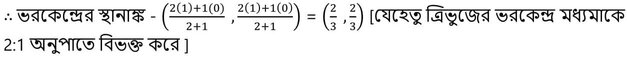
∴ ভরকেন্দ্রের স্থানাঙ্ক (2/3,2/3) ।
WBBSE Class 9 Math Koshe Dekhi 20|ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল কষে দেখি -20
(ii) একটি ত্রিভুজের ভরকেন্দ্রের স্থানাঙ্ক (6,9) এবং দুটি শীর্ষবিন্দুর স্থানাঙ্ক (15,0) এবং (0,10) তৃতীয় শীর্ষবিন্দুর স্থানাঙ্ক নির্ণয় করি ।
সমাধানঃ
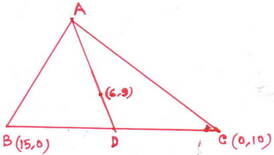
ধরা যাক , ABC একটি ত্রিভুজ যার ভরকেন্দ্রের স্থানাঙ্ক (6,9) এবং B ও C বিন্দুদ্বয়ের স্থানাঙ্ক যথাক্রমে (15,0) এবং (0,10) ।ধরি , A বিন্দুর স্থানাঙ্ক (x,y ) এবং BC বাহুর মধ্যবিন্দু D ।
BC বাহুর মধ্যবিন্দু (D ) এর স্থানাঙ্ক – ( 15/2 , 10/2 )= (15/2, 5 )
ভরকেন্দ্র AD মধ্যমাকে 2:1 অনুপাতে বিভক্ত করে ।
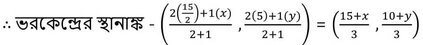
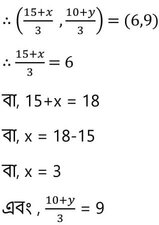
বা, 10+y = 27
বা, y = 27- 10
বা, y = 17
∴ A বিন্দুর স্থানাংক (3,17 ) ।
(iii) (a,0) ,(0,b) এবং (1,1) বিন্দু তিনটি সমরেখ হলে দেখাই যে , 1/a +1/b =1
সমাধানঃ (a,0) ,(0,b) এবং (1,1) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ক্ষেত্রফল –
= ½ |a (b-1) + 0 (1-0) + 1(0-b)| বর্গএকক
= ½ | (ab-a – b)| বর্গএকক
∴ যেহেতু , (a,0) ,(0,b) এবং (1,1) বিন্দু তিনটি সমরেখ
∴ ½ | (ab-a – b)| = 0
বা, ½ (ab-a-b) = 0
বা, ab –a – b = 0
বা , ab = a+b
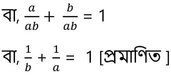
(iv) (1,4) , (-1,2) এবং (-4,1) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল নির্ণয় করো ।
সমাধানঃ (1,4) , (-1,2) এবং (-4,1) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল –
= ½ |1(2-1) + (-1) (1-4 ) + (-4) (4-2)| বর্গএকক
= ½ |1+ 3 -8| বর্গএকক
= ½ |-4 |বর্গএকক
= ½ ✕ 4 বর্গএকক
= 2 বর্গএকক
∴ (1,4) , (-1,2) এবং (-4,1) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল 2 বর্গএকক ।
(v) (x-y ,y-z) ,(-x,-y) এবং (y ,z) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ভরকেন্দ্রের স্থানাঙ্ক লিখি ।
সমাধানঃ (x-y ,y-z) ,(-x,-y) এবং (y ,z) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ভরকেন্দ্রের স্থানাঙ্ক –
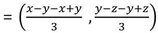
= (0 ,0)
∴ (x-y ,y-z) ,(-x,-y) এবং (y ,z) বিন্দু তিনটি দ্বারা গঠিত ত্রিভুজের ভরকেন্দ্রের স্থানাঙ্ক (0 ,0) ।
WBBSE Class 9 Math Koshe Dekhi 20|ত্রিভুজাকৃতি ক্ষেত্রের ক্ষেত্রফল কষে দেখি -20
This page is very good.The questions are very easy type.
Thanks