WBBSE Class 9 Math Koshe Dekhi 21|লগারিদম কষে দেখি 21

WBBSE Class 9 Math Koshe Dekhi 21|লগারিদম কষে দেখি 21|গণিত প্রকাশ নবম শ্রেণি(ক্লাস ৯)কষে দেখি ২১ সমাধান|Ganit Prakash Class 9(IX) Logarithm Exercise 21 Solution.

গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।

গণিত প্রকাশ দশম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।

WBBSE OFFICIAL SITE

WBBSE Class 9 Math Koshe Dekhi 21|লগারিদম কষে দেখি 21 গণিত প্রকাশ নবম শ্রেণি (ক্লাস ৯) কষে দেখি ২১ সমাধান ।Gonit Prokash Class 9(IX) Logarithm Exercise 21 Solution.

লগারিদম -এর প্রয়োজনীয় সূত্রাবলী|Logarithm Formula

(i) log_aMN = log_aM +log_aN

(ii) log_a(M/N) =log_aM – log_aN

(iii) log_aM^N = N log_aM

(iv) log_aM =log_bM ✕ log_ab

(v) log_a1 = 0

(vi) log_aa = 1

(vi) a^Log_aM =M

(vii) log_ab ✕ log_ba =log_aa =1

(viii) log_ba = 1/ log_ab

(ix) log_bM = log_aM / log_ab

(x) log_a (1/a) = -1

(xi) যদি log_aM = log_aN হয় , তবে M =N

Koshe Dekhi-21 |কষে দেখি ২১

1. মান নির্ণয় করিঃ

(ii) log_0.01 0.000001

সমাধানঃ ধরি , log_0.01 0.000001 = x

বা, (0.01)^x = 0.000001

বা, (0.01)^x = (0.01)³

বা, x = 3

∴  log _0.01 0.000001 = 3

(iii) log_√6216

সমাধানঃ ধরি , log_√6216 = x

বা, ( √6)^x = 216

বা, (√6)^x = (6)³

বা, (√6)^x  = {(√6)²} ³

বা, (√6)^x  = (√6 )⁶

বা, x = 6

∴ log_√6 216 = 6

(iv) log _2√3 1728

সমাধানঃ

ধরি , log _2√3 1728

বা, (2√3)^x = 1728

বা, (2√3)^x = 2⁶✕3³

বা, (2√3)^x = 2⁶ ✕ {(√3)²}³

বা, (2√3)^x = 2⁶ ✕ (√3)⁶

বা, (2√3)^x = (2√3)⁶

বা, x = 6

∴ log _2√3 1728 = 6  

WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

2.

(a) 625 –এর লগারিদম 4 হলে , নিধান কী হবে হিসাব করে লিখি ।

সমাধানঃ ধরি , নিধান x ।

∴ log_x 625 = 4

বা, (x)⁴ = 625

বা, (x)⁴ = (5)⁴

বা, x = 5

∴ নিধান 5 ।

WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

(b) 5832 –এর লগারিদম 6 হলে , নিধান কী  হবে হিসাব করে লিখি ।

সমাধানঃ ধরি , নিধান = x

∴ log _x 5832 = 6

বা, x⁶ = 5832

বা, x⁶ = 2³ ✕ 3⁶

বা, x⁶ = (√2)⁶ ✕ 3⁶

বা, x⁶ = (3√2)⁶

বা, x = 3√2

∴ নিধান = 3√2

WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

3(a) 1 +log₁₀a =2log₁₀b হলে , a কে b দ্বারা প্রকাশ করি ।

সমাধানঃ

1 +log₁₀a =2log₁₀b

বা, log₁₀10 + log₁₀a =log₁₀b² [যেহেতু , log_aa =1 এবং Nlog_aM = log_aM^N ]

বা, log₁₀(10a) = log₁₀b² [যেহেতু,log_aM+log_aN = log_aMN]

বা, 10a = b² [যেহেতু , log_aM =log_aN ⇒ M=N]

বা, a = 1/10 b² [উত্তর ]

WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

(b) 3+log₁₀x = 2log₁₀y হলে, x কে y দ্বারা প্রকাশ করো ।

সমাধানঃ 

3+log₁₀x = 2log₁₀y

বা, 3log₁₀10 + log₁₀x = 2log₁₀y [যেহেতু , log₁₀10 =1 ]

বা, log₁₀10³ + log₁₀x = log₁₀y² [যেহেতু , Nlog_aM = log_aM^N ]

বা, log₁₀ 1000 + log₁₀x = log₁₀y²

বা, log₁₀ 1000x = log₁₀y²

বা, 1000x = y²

বা, x = y²/1000 [উত্তর ]

WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

4. মান নির্ণয় করিঃ

(a) log₂ [log₂{log₃(log₃27³)}]

সমাধানঃ

log₂ [log₂{log₃(log₃27³)}]

= log₂ [log₂{log₃(3log₃27)}] [যেহেতু,Nlog_aM = log_aM^N ]

= log₂ [log₂{log₃(3log₃3³)}]

= log₂ [log₂{log₃(9log₃3)}] [যেহেতু,Nlog_aM = log_aM^N ]

= log₂ [log₂{log₃9}] [যেহেতু,log_aa =1]

= log₂ [log₂{log₃3²}]

= log₂ [log₂{2log₃3}] [যেহেতু,Nlog_aM = log_aM^N ]

= log₂ [log₂2 ] [যেহেতু,log_aa =1]

= log₂ 1 [যেহেতু,log_aa =1]

= 0 [log_a1 = 0] [উত্তর ]

WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

(c ) log₃4 ☓ log₄5 ☓ log₅6 ☓ log₆7 ☓ log₇3

সমাধানঃ

উত্তরঃ 1

WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

= log₁₀ 384 – log₁₀ 5 + log₁₀ 81 – log₁₀ 32 +3(log₁₀ 5 –log₁₀ 3) +log₁₀ 1 – log₁₀9

= log₁₀ (2⁷☓3) – log₁₀ 5 + log₁₀ (3⁴) –log₁₀ (2⁵) +3log₁₀ 5 –3log₁₀ 3 + log₁₀ 1 – log₁₀(3²)

= 7log₁₀2 +log₁₀3 –log₁₀5+4log₁₀3 -5log₁₀2 +3log₁₀5 -3log₁₀3 +log₁₀1 -2log₁₀3 [যেহেতু , Nlog_aM = log_aM^N এবং log_a(MN)=log_aM+log_aN]  ]

= 2log₁₀2 +5 log₁₀3 -5 log₁₀3 +2 log₁₀5+log₁₀1

= 2(log₁₀2 + log₁₀5) [যেহেতু , log_a1 = 0]

=2 log₁₀ (2☓5) [যেহেতু,log_a(MN)=log_aM+log_aN] 

= 2 log₁₀

= 2 [যেহেতু, log_aa=1]  [উত্তর]

WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

5. প্রমাণ করিঃ

(i) log (75/16) – log (5/9) + log (32 /243) = log2

সমাধানঃ

= log 75 – log16 –2(log 5-log 9) +log 32 – log243 [যেহেতু ,log_a(M/N) = log_aM -log_aN]

= log 75 – log16 –2log 5+2log 9 +log 32 – log243

= log(5²✕3) – log(2⁴) -2log5 +2log(3²) +log(2⁵) -log(3⁵)

= 2log 5+log3 –4log2-2log5 +4log3 +5log2 -5log3 [যেহেতু , Nlog_aM = log_aM^N এবং log_a(MN)=log_aM+log_aN]

= log2 [প্রমাণিত ]

WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

(ii) log₁₀15(1+log₁₅30) +1/2 log₁₀16(1+log₄7) –log₁₀6(log₆3+1+log₆7) = 2

সমাধানঃ

log₁₀15(1+log₁₅30) +1/2 log₁₀16(1+log₄7) –log₁₀6(log₆3+1+log₆7)

= log₁₀15  + log₁₀15 ☓ log₁₅30 +1/2log₁₀16 +1/2 log₁₀16 ☓ log₄7 – log₁₀6 ☓ log₆3 – log₁₀6 -log₁₀6 ☓ log₆7

= log₁₀15  + log₁₀15 ☓ log₁₅30 +log₁₀ (16) ^1/2+ log₁₀(16)^1/2 ☓ log₄7 – log₁₀6 ☓ log₆3 – log₁₀6 ☓ log₁₀6 ☓ log₆7

= log₁₀15  + log₁₀15 ☓ log₁₅30 +log₁₀ {(4)²} ^1/2+ log₁₀ {(4)²}^1/2 ☓ log₄7 – log₁₀6 ☓ log₆3 – log₁₀6 – log₁₀6 ☓ log₆7

= log₁₀15  + log₁₀15 ☓ log₁₅30 +log₁₀ 4+ log₁₀ 4 ☓ log₄7 – log₁₀6 ☓ log₆3 – log₁₀6 – log₁₀6 ☓log₆7

= log₁₀15  + log₁₀15 ☓ log₁₅(3☓10) +log₁₀ 4+ log₁₀ 4 ☓ log₄7 – log₁₀6 ☓ log₆3 – log₁₀6 – log₁₀6 ☓ log₆7

= log₁₀15  + log₁₀15 ☓ (log₁₅3+ log₁₅10) +log₁₀ 4+ log₁₀ 4 ☓ log₄7 – log₁₀6 ☓ log₆3 – log₁₀6 – log₁₀6 ☓ log₆7

= log₁₀15  + log₁₀15 ☓ log₁₅3+ log₁₀15 ☓ log₁₅10 +log₁₀ 4+ log₁₀ 4 ☓ log₄7 – log₁₀6 ☓ log₆3 – log₁₀6 – log₁₀6 ☓ log₆7

= log₁₀15  + log₁₀ 3 + 1 +log₁₀ 4+ log₁₀ 7- log₁₀3- log₁₀6 – log₁₀7 [log_aM✕ log_MN = log_aN]

=  log₁₀15  + log₁₀ 3 + log₁₀10 +log₁₀ 4+ log₁₀ 7- log₁₀3-log₁₀6 – log₁₀7

= log ₁₀ (15☓3☓10☓4☓7) –log₁₀ (3☓6☓7) [log_aM+log_aN=log_a(MN) ]

= log₁₀ 12600 –log₁₀ 126

= log₁₀ (12600/126)

= log₁₀ 100

= log₁₀ 10²

= 2 log₁₀ 10 [Nlog_aM = log_aM^N ]

= 2 [প্রমাণিত ] [যেহেতু , log _aa =1 ]

WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

(iii) log₂log₂log₄256+2log_√2 2 =5

সমাধানঃ

log₂log₂log₄256+2log_√2 2

= log₂log₂log₄256+2log_√2 (√2)²

= log₂log₂log₄256+4 log_√2 √2 [যেহেতু , Nlog_aM = log_aM^N ]

= log₂log₂log₄256+4 [ যেহেতু , log_aa =1]

= log₂log₂log₄ (4)⁴+4

= log₂log₂ 4 log₄ 4+4 [যেহেতু , Nlog_aM = log_aM^N ]

= log₂log₂ 4 +4 [ যেহেতু , log_aa =1]

= log₂log₂ 2² +4

= log₂2log₂ 2 +4 [যেহেতু , Nlog_aM = log_aM^N ]

= log₂2 +4 [ যেহেতু , log_aa =1]

= 1+4 [ যেহেতু , log_aa =1]

= 5 [প্রমাণিত ]

WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

(iv) log _x² x ☓ log_y² y ☓ log_z² z

সমাধানঃ

log _x² x ☓ log_y² y ☓ log_z² z

WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

(v) log_b³ a ☓ log_c³ b ☓ log_a³ c = 1/27

সমাধানঃ

log_b3a ☓ log_c3b ☓log_a3c

WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

(vi) 1/log_xy(xyz) + 1/log_yz(xyz) +1/log_zx(xyz) =2

সমাধানঃ

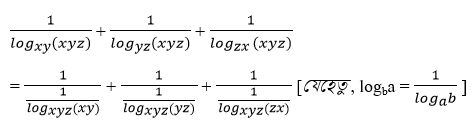
= log_xyz xy +log _xyz yz +log _xyz zx

= log _xyz (xy ✕ yz ✕ zx) [যেহেতু ,log_a (MN) =log_aM+log_aN]

= log _xyz (x²y²z²)

= log xyz (xyz)²

= 2 log _xyz xyz [যেহেতু , Nlog_aM = log_aM^N ]

= 2 [প্রমাণিত ][ যেহেতু , log_aa =1]

WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

(vii) log (a²/bc) +log(b²/ca) +log(c²/ab) = 0

সমাধানঃ

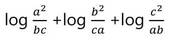
= loga² –logbc +logb² –log ca +logc²– logab [log_a (M/N) =log_a M-log_aN]

= loga²+logb²+logc² – logbc –logca-logab

= log (a²b²c²) – log(bc´ca´ab)

= log (abc)² –log (abc)²

= 0 [প্রমাণিত ]

WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

(viii) x^logy-logz ☓ y ^logz-logx ☓ z ^logx-logy =1

সমাধানঃ

x^logy-logz ☓ y ^logz-logx ☓ z ^logx-logy

ধরি , P =  x^logy-logz ☓ y ^logz-logx ☓ z ^logx-logy

উভয়পক্ষে log নিয়ে পাই ,

logP = log (x^logy-logz ☓ y ^logz-logx ☓ z ^logx-logy)

বা, logP = log x^logy-logz + log y ^logz-logx +log z ^logx-logy 

বা, logP = (logy –logz)logx +(logz- logx)logy + (logx –logy)logz [যেহেতু , Nlog_aM = log_aM^N ]

বা, logP = logylogx – logzlogx +logzlogy –logxlogy+logxlogz –logylogz

বা, logP = 0

বা, logP = log1 [যেহেতু ,log1 =0]

বা, P = 1

∴ x^logy-logz ☓ y ^logz-logx ☓ z ^logx-logy =1 [প্রমাণিত ]

WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।

6. (i) যদি log (x+y) /5 = ½(logx+logy ) হয় , তবে দেখাই যে , x/y +y/x = 23

সমাধানঃ

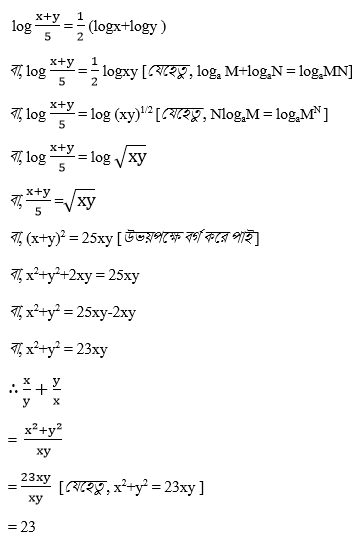
WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

(ii) যদি , a⁴+b⁴ = 14a²b² হয় , তাহলে দেখাই যে , log(a²+b²) =loga +logb+2log2

সমাধানঃ

a⁴+b⁴ = 14a²b²

বা, (a²)² +(b²)² = 14a²b²

বা, (a²+b²)² -2a²b² = 14a²b²

বা, (a²+b²)² = 16a²b²

বা, (a²+b²)² =  (4ab)²

বা, (a²+b²) = 4ab

∴ log(a²+b²)

= log (4ab)

= log4+loga+logb

= log 2² +loga +logb

= 2log2 +loga +logb

= loga +logb+2log2 [প্রমাণিত ]

WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

7. যদি , logx / y-z = logy / z-x = logz / x-y হয় , তাহলে দেখাই যে , xyz=1

সমাধানঃ

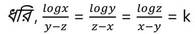
[যেখানে K(≠0) একটি সমানুপাতিক ধ্রুবক ]

∴ logx = k (y-z) ,logy =k(z-x)

এবং log z= k (x-y)

∴ logx+logy+logz = k(y-z)+k(z-x)+k(x-y)

বা, log (xyz) = k(y-z+z-x+x-y) [যেহেতু ,log_a (MN)= log_aM+log_aN]

বা, log(xyz) = 0

বা, log(xyz) = log 1[যেহেতু ,log1 =0]

বা, xyz = 1 [প্রমাণিত ]

WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

8. যদি , logx /b-c = logy / c-a = logz / a-b হয় , তাহলে প্রমাণ করি যে ,

(a) x ^b+c . y^c+a. z ^a+b =1

(b) x ^{b^2+bc+c^2} . y^{c^2+ca+a^2}. Z ^{a^2+ab+b^2} =1

সমাধানঃ

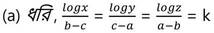
[যেখানে K(≠0) একটি সমানুপাতিক ধ্রুবক ]

∴logx = k(b-c)

বা, (b+c) logx = k(b-c)(b+c)

বা, (b+c) logx = k(b²-c²) —(i)

এবং ,  logy = k(c-a)

বা, (c+a) logy = k(c+a)(c-a)

বা, (c+a) logy = k(c²-a²) —(ii)

এবং logz = k(a-b)

বা, (a+b) logz =  k (a-b)(a+b)

বা, (a+b) logz = k(a²-b²) —(iii)

∴  log (x ^b+c . y^c+a. z ^a+b)

= log x ^b+c +logy ^c+a + log z ^a+b

= (b+c) logx +(c+a) logy +(a+b) logz [যেহেতু ,NlogM=logM^N ]

= k(b²-c²) +k(c²-a²) +k(a²-b²) [(i) ,(ii) ও(iii) থেকে পাই ]

= k( b²-c²+c²-a² +a²-b²)

= k. 0

= 0

= log 1

∴ log (x ^b+c . y^c+a. z ^a+b) = log1

বা, (x ^b+c . y^c+a. z ^a+b) =  1 [প্রমাণিত ]

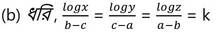
[যেখানে K(≠0) একটি সমানুপাতিক ধ্রুবক ]

∴logx = k(b-c)

বা, (b²+bc+c²)logx = k(b-c) (b²+bc+c²)

বা, (b²+bc+c²)logx = k(b³-c³) —(i)

 logy = k(c-a)

বা, (c²+ca+a²) logy = k(c-a) (c²+ca+a²)

বা, (c²+ca+a²) logy = k(c³-a³) —(ii)

এবং logz = k(a-b)

বা, (a²+ab+b²) logz =  k (a-b) (a²+ab+b²)

বা, (a²+ab+b²) logz = k(a³-b³) —(iii)

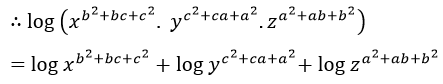
= (b²+bc+c²) logx +(c²+ca+a²) logy +(a²+ab+b²) logz

= k (b³-c³) +k(c³-a³) +k(a³-b³) [ (i) ,(ii) ও (iii) থেকে পাই ]

= k(b³-c³-c³-a³ +a³-b³)

= k.0

= 0

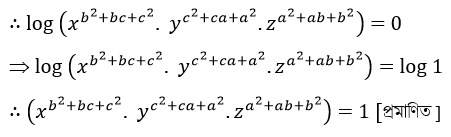
WBBSE Class 9 Math Koshe Dekhi 21. লগারিদম কষে দেখি 21

9. যদি , a ^3-x . b^5x = a^5+x . b^3x হয় , তাহলে দেখাই যে , x log (b/a)= loga

সমাধানঃ

a ^3-x . b^5x = a^5+x . b^3x

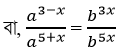
বা, a ^{3-x -5-x} = b^3x-5x

বা, a ^-2-2x = b ^-2x

বা, a^-2 . a^-2x = b^-2x

বা, a ^-2 = (b/a)^-2x

উভয়পক্ষে log নিয়ে পাই ,

Log a^-2 = log (b/a) ^-2x

বা, -2 loga = -2x log (b/a) [যেহেতু, NlogM= logM^N]

বা, loga = xlog(b/a) [প্রমাণিত]

10. সমাধান করিঃ  

(a) log₈ [log₂{log₃ (4^x+17)}] = 1/3

সমাধানঃ

log₈ [log₂{log₃ (4^x+17)}] = 1/3

বা, (8) ^1/3 = log₂{log₃(4^x+17)}

বা, (2)³☓ ^1/3 = log₂{log₃(4^x+17)}

বা, 2 = log₂{log₃(4^x+17)}

বা,  log₃(4^x+17)} =2²

বা, log₃(4^x+17)} = 4

বা, (4^x+17)} = (3)⁴

বা, 4^x+17 = 81

বা, 4^x= 81-17

বা, 4^x = 64

বা, 4^x = (4)³

বা, x = 3

∴ নির্ণেয় সমাধান x = 3 ।

(b) log₈x +log₄x+log₂x = 11

সমাধানঃ

log₈x +log₄x+log₂x = 11

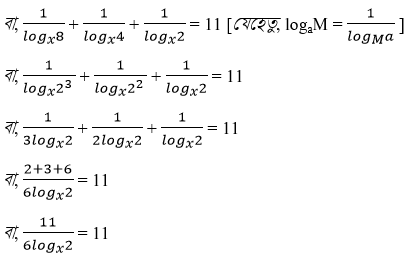
বা, 11☓ log_x2 = 11☓6

বা, log₂x = 6 [যেহেতু, log_aM = 1/ log_M a ]

বা, 2⁶ =x

বা, x = 64

∴ নির্ণেয় সমাধান x = 64 ।

11. দেখাই log ₁₀2 –এর মান ¼ এবং 1/3 এর মধ্যে অবস্থিত ।

সমাধানঃ

ধরি ,  log ₁₀2 = x

∴ (10)^x = 2

বা, (10 )^12x = 2¹² = 4096

আবার , 1000 < 4096  < 10000

বা, 10³ < 2¹² < 10⁴

বা, 10³ < 10^12x < 10⁴

বা, 3 < 12x < 4

বা, 3/12 < x < 4/12

বা ,1/4 < x < 1/3 [প্রমাণিত ]

গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।

12. বহু বিকল্পীয় প্রশ্ন (M.C.Q.)

(i) যদি , log_√x 0.25 = 4 হয় , তাহলে x এর মান

(a) 0.5

(b) 0.25

(c ) 4

(d) 16

Ans: (a) 0.5

সমাধানঃ 

log_√x 0.25 = 4

বা, (√x )⁴ = 0.25

বা, (√x )⁴ = 0.25

বা, x² = 0.25

বা, x² = (0.5)²

বা, x = 0.5

(ii) log₁₀ (7x-5) = 2 হলে , x –এর মান

(a) 10

(b) 12

(c ) 15

(d) 18

Ans: (c ) 15

সমাধানঃ

log₁₀ (7x-5) = 2

বা, 10 ² = 7x-5

বা, 7x-5 = 100

বা, 7x = 105

বা, x = 105/7

বা, x = 15

(iii) log₂3 = a হলে, log₈27 হবে

(a) 3a

(b) 1/a

(c ) 2a

(d) a

Ans:  (d) a

সমাধানঃ

log₂3 = a

বা, 2^a = 3

∴ log₈27

= log ₈ (3)³

= 3log₈(3)

= 3log₈(2^a)

= 3a log₈2

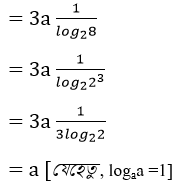
= a [যেহেতু , log_aa =1]

(iv) log_√2 x = a হলে, log_2√2 x হবে

(a) a/3

(b) a

(c ) 2a

(d) 3a

Ans: (a) a/3

সমাধানঃ   

log_√2 x = a

∴ (√2)^a = x

∴ log_2√2 x

= log_2√2(√2)^a

= a log_2√2 (√2)

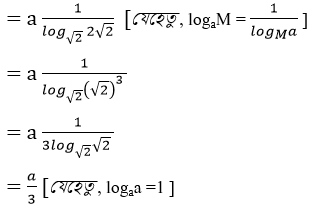
(v) log _x 1/3 = -1/3 হলে, x-এর মান হবে

(a) 27

(b) 9

(c ) 3

(d) 1/27

Ans: (a) 27

সমাধানঃ

log _x 1/3 = -1/3

বা, x^-1 = (27)^-1

বা, x =27

13.সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ

(i) log₄log₄ log₄ 256-এর মান কত হবে হিসাব করে লিখি ।

সমাধানঃ

log₄log₄ log₄ 256

= log₄log₄ log₄ 4⁴

= log₄log₄ 4log₄ 4

= log₄log₄ 4  [যেহেতু,log_aa =1]

= log₄1 [যেহেতু,log_aa =1]

= 0 [ যেহেতু,log 1 =0] [উত্তর ]

(ii) log (aⁿ/bⁿ) + log (bⁿ/cⁿ) +log(cⁿ/aⁿ) –এর মান কত হবে হিসাব করে লিখি ।

সমাধানঃ

= 0 [উত্তর]

(iii) দেখাই যে , a^log_ax = x

সমাধানঃ ধরি ,log_ax = u

∴ a^u = x

∴ a^log_ax

= a^u

= x

∴ a^log_ax = x [প্রমাণিত ]

(iv) log_e2  . log_x 25 = log ₁₀ 16 . log_e 10 হলে x –এর মান কত ?

সমাধানঃ

log_e2 . log_x 25 = log ₁₀ 16 . log_e 10

বা, log_e2 . log_x 25  = log _e 16

বা, log_e2 . log_x 25 = log _e (2)⁴

বা, log_e2 . log_x 25 = 4log _e (2) [যেহেতু , Nlog_aM = loga M^N ]

বা, log_x 25 = 4log _e (2) / log_e2

বা,  log_x 25 = 4

বা, x⁴ = 25

বা, x⁴ = (√5)⁴

বা, x = √5

∴ x = √5 [উত্তর]

গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।

ধন্যবাদ। এই POST টি আপনাদের ভালো লাগলে SHARE করার অনুরোধ রইল । এইরকম সুন্দর সুন্দর POST পেতে , আমাদের FACEBOOK PAGE টি LIKE করুন ।