WBBSE Class 9 Math Koshe Dekhi 5.5|রৈখিক সহ সমীকরণ কষে দেখি 5.5

WBBSE Class 9 Math Koshe Dekhi 5.5|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) কষে দেখি 5.5|পরিবর্ত পদ্ধতি |Simultaneous Linear Equation Substitution Method|গণিত প্রকাশ নবম শ্রেণি (ক্লাস ৯)|কষে দেখি ৫.৫|WBBSE Class IX Gonit Prokash Somadhan

গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।

মাধ্যমিক গণিত প্রকাশ (দশম শ্রেণি ) বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।

WBBSE OFFICIAL SITE

WBBSE Class 9 Math Koshe Dekhi 5.5|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) কষে দেখি 5.5|পরিবর্ত পদ্ধতি |Simultaneous Linear Equation Substitution Method|গণিত প্রকাশ নবম শ্রেণি (ক্লাস ৯)|কষে দেখি ৫.৫|WBBSE Class IX Gonit Prokash Somadhan

কষে দেখি 5.5

সমাধানঃ

সমাধানঃ

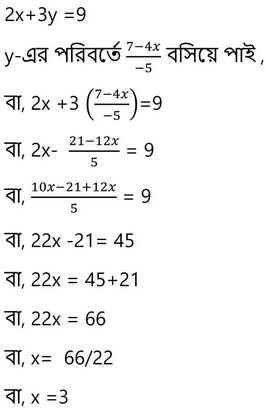
3.নীচের দুইচলবিশিষ্ট সমীকরণগুলি পরিবর্ত পদ্ধতিতে সমাধান করি ও লেখচিত্রের সাহায্যে সমাধান করে যাচাই করি ।

(a) 3x-y =7 ,2x +4y = 0

সমাধানঃ প্রদত্ত সমীকরণদ্বয় হল –

3x-y =7 —(i) 

2x +4y = 0 —(ii)

(i) নং সমীকরণ থেকে পাই ,

3x –y = 7

বা, 3x = 7+y

বা, x = (7+y) /3 —(iii)

(iii) নং সমীকরণ থেকে প্রাপ্ত x এর মান (ii) নং সমীকরণে x-এর পরিবর্তে বসিয়ে পাই ,

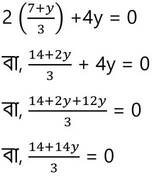
বা, 14y +14 = 0

বা, 14y = -14

বা, y = -14/14

বা, y = -1

y এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই ,

x = {7+(-1)} /3 = (7-1)/3 =6/3 = 2

∴ নির্ণেয় সমাধান x = 2 এবং y = -1

লেখচিত্রের মাধ্যমে সমাধানঃ

3x-y =7 —(i) 

2x +4y = 0 —(ii)

(i) নং সমীকরণ থেকে পাই ,

3x –y = 7

বা, 3x = 7+y

বা, x = (7+y) /3

x	3	4	5
y	2	5	8

(ii) নং সমীকরণ থেকে পাই ,

2x +4y = 0

বা, 2x = -4y

বা, x = -2y

x	-10	10	-14
y	5	-5	7

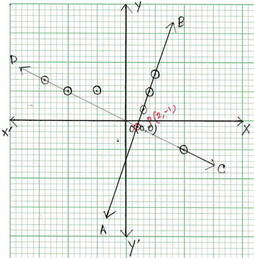
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অঙ্কন করে ,ক্ষুদ্রতম বর্গক্ষেত্রের প্রতিটি বাহুকে 1 একক ধরে (3,2) ,(4,5) এবং (5,8) বিন্দুগুলি স্থাপন করে ও যুক্ত করে  AB সরলরেখা এবং  (-10 ,5) ,( 10 ,-5) এবং (-14,7) বিন্দুগুলি স্থাপন করে  ও যুক্ত করে CD সরলরেখা অঙ্কন করা হল । সরলরেখা দুটি পরস্পর P বিন্দুতে ছেদ করে । P বিন্দুর স্থানাঙ্ক ( 2,-1) ।

 ∴ নির্ণেয় সমাধান x = 2 এবং y = -1

∴ পরিবর্ত পদ্ধতিতে নির্ণেয় সমাধান এবং লেখচিত্রের মাধ্যমে নির্ণেয় সমাধান দুটি সমান ।

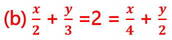
সমাধানঃ

(iii) নং সমীকরণ থেকে প্রাপ্ত x এর মান (ii) নং সমীকরণে x-এর পরিবর্তে বসিয়ে পাই ,

y – এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই ,

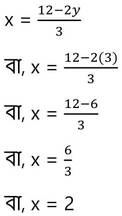
∴ নির্ণেয় সমাধান  x = 2 এবং y = 3

লেখচিত্রের মাধ্যমে সমাধানঃ

x	0	2	6
y	6	3	-3

x	0	2	14
y	4	3	-3

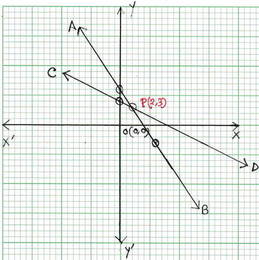
ছক কাগজে XOX´ ও YOY´ দুটি পরস্পর লম্ব অঙ্কন করে , ক্ষুদ্রতম  বর্গক্ষেত্রের প্রতিটি বাহুকে 1 একক ধরে (0,6) ,(2,3) এবং (6,-3) বিন্দুগুলি স্থাপন করে ও যুক্ত করে  AB সরলরেখা এবং  (0,4) ,(2,3) এবং (14 ,-3) বিন্দুগুলি স্থাপন করে  ও যুক্ত করে CD সরলরেখা অঙ্কন করা হল । সরলরেখা দুটি পরস্পর P বিন্দুতে ছেদ করে । P বিন্দুর স্থানাঙ্ক ( 2, 3) ।

 ∴ নির্ণেয় সমাধান x = 2 এবং y = 3

∴ পরিবর্ত পদ্ধতিতে নির্ণেয় সমাধান এবং লেখচিত্রের মাধ্যমে নির্ণেয় সমাধান দুটি সমান ।

4. নীচের দুইচলবিশিষ্ট সহসমীকরণগুলি পরিবর্ত পদ্ধতিতে সমাধান করি ও সমাধানের মানগুলি সমীকরণগুলিকে সিদ্ধ করে কিনা  যাচাই করি ।

(iii) নং সমীকরণ থেকে প্রাপ্ত x এর মান (ii) নং সমীকরণে x-এর পরিবর্তে বসিয়ে পাই ,

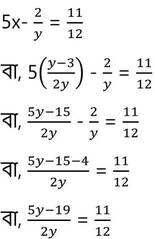
বা, 12(5y -19) = 22y

বা, 60 y – 228 = 22y

বা, 60y -22y = 228

বা, 38y = 228

বা, y = 228/38

বা, y = 6

y – এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই ,

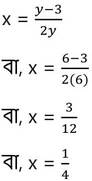
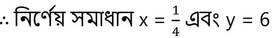
সমাধানের মানগুলি প্রদত্ত সমীকরণ গুলিকে সিদ্ধ করে কিনা দেখিঃ –

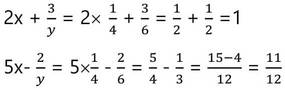
∴ নির্নেয় সমাধান গুলি প্রদত্ত সমীকরণদ্বয়কে সিদ্ধ করে ।

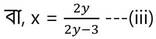
(iii) নং সমীকরণ থেকে প্রাপ্ত x এর মান (ii) নং সমীকরণে x-এর পরিবর্তে বসিয়ে পাই ,

বা, 6(10y+5) = 70y

বা, 60y +30 = 70y

বা, 60y -70y = -30

বা, – 10y = -30

বা, y = -30 /-10

বা , y = 3

y –এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই ,

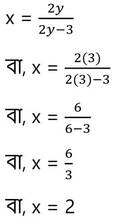
∴ নির্ণেয় সমাধান x = 2 ,y = 3

সমাধানের মানগুলি প্রদত্ত সমীকরণ গুলিকে সিদ্ধ করে কিনা দেখিঃ –

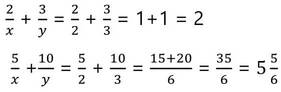
∴ নির্নেয় সমাধান গুলি প্রদত্ত সমীকরণদ্বয়কে সিদ্ধ করে ।

(iii) নং সমীকরণ থেকে প্রাপ্ত x এর মান (ii) নং সমীকরণে x-এর পরিবর্তে বসিয়ে পাই ,

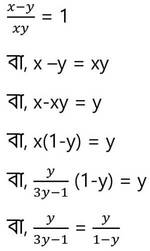
বা, 3y-1 = 1-y

বা, 3y+y = 1+1

বা, 4y = 2

বা, y = 2/4

বা, y = ½

y এর প্রাপ্ত মান (iii) নং সমিকরণে বসিয়ে পাই ,

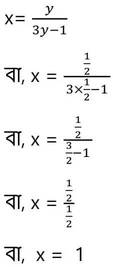
∴ নির্ণেয় সমাধান x = 1,y = ½

সমাধানের মানগুলি প্রদত্ত সমীকরণ গুলিকে সিদ্ধ করে কিনা দেখিঃ –

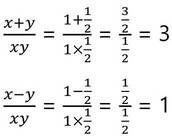
∴ নির্নেয় সমাধান গুলি প্রদত্ত সমিকরণদ্বয়কে সিদ্ধ করে ।

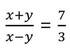
বা, 3(x+y) = 7(x-y)

বা, 3x+3y =7x-7y

বা, 3x-7x = -3y -7y

বা, -4x = -10y

বা , x = -10y/ -4

বা, x = 5y /2 —(iii)

(iii) নং সমীকরণ থেকে প্রাপ্ত x এর মান (ii) নং সমীকরণে x-এর পরিবর্তে বসিয়ে পাই ,

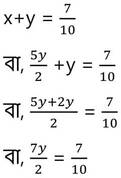
বা, 70y = 14

বা, y = 14/70

বা, y = 1/5

y –এর প্রাপ্ত মান (iii) নং সমিকরণে বসিয়ে পাই ,

x = 5y /2

সমাধানের মানগুলি প্রদত্ত সমীকরণ গুলিকে সিদ্ধ করে কিনা দেখিঃ –

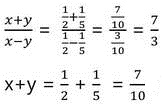
∴ নির্নেয় সমাধান গুলি প্রদত্ত সমীকরণদ্বয়কে সিদ্ধ করে ।

গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।

5. নীচের দুইচলবিশিষ্ট সহসমীকরণগুলি  পরিবর্ত পদ্ধতিতে সমাধান করি ।

(i) 2(x-y) = 3 , 5x+8y = 14

সমাধানঃ

2(x-y) = 3 —(i)

 5x+8y = 14 —(ii)

(i) নং সমীকরণ থেকে পাই ,

2(x-y) = 3

বা, 2x -2y =3

বা, 2x = 2y+3

বা, x =  —(iii)

(iii) নং সমীকরণ থেকে প্রাপ্ত x এর মান (ii) নং সমীকরণে x-এর পরিবর্তে বসিয়ে পাই ,

5x+8y = 14

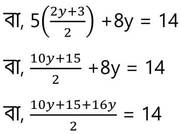
বা, 26y+15  = 28

বা, 26y = 13

বা, y = 13/26

বা, y = ½

y –এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই ,

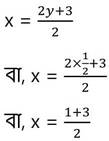
বা, x = 4/2

বা, x= 2

∴ নির্ণেয় সমাধান x = 2 এবং y = ½

বা, 25y – 19 = 6y

বা, 25y- 6y =19

বা, 19y = 19

বা, y = 19/19

বা, y =1

y-এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই ,

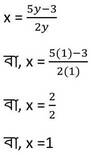
∴ নির্ণেয় সমাধান x = 1,y =1

সমাধানঃ প্রদত্ত সমীকরণদ্বয় হল –

(iii) নং সমীকরণ থেকে প্রাপ্ত x এর মান (ii) নং সমীকরণে x-এর পরিবর্তে বসিয়ে পাই ,

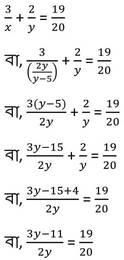
বা, 20(3y -11) = 38y

বা, 60y – 220 = 38y

বা, 60y -38y = 220

বা, 22y = 220

বা, y = 220 /22

বা, y = 10

y – এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই ,

বা, 4 (x-y) = 3(y-1)

বা, 4x -4y = 3y -3

বা, 4x = 4y+3y -3

বা, 4x = 7y -3

বা, x = (7y-3)/4 —(iii)

(iii) নং সমীকরণ থেকে প্রাপ্ত x এর মান (ii) নং সমীকরণে x-এর পরিবর্তে বসিয়ে পাই ,

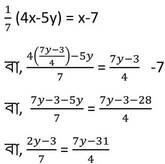
বা, 4(2y-3) = 7(7y-31)

বা, 8y – 12 = 49y – 217

বা, 8y -49y = 12 – 217

বা, -41y =  -205

বা, y = -205 /-41

বা, y = 5

y –এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই ,

∴ নির্ণেয় সমাধান x = 8 এবং y = 5

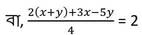
বা, 2x+2y +3x-5y = 8

বা, 5x -3y = 8

বা, 5x = 3y+8

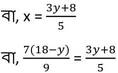
বা, 35 (18-y) = 9(3y+8)

বা, 630 -35y = 27y +72

বা, -35y -27y = -630 +72

বা, -62 y = -558

বা, y = -558 / -62

বা, y = 9

y –এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই ,

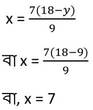
∴ নির্ণেয় সমাধান x = 7, y = 9

(viii) p(x+y) =q(x-y) = 2pq

সমাধানঃ প্রদত্ত সমীকরণদ্বয় হল –

p(x+y) = 2pq —(i)

এবং q(x-y) = 2pq —(ii)

(i) নং সমীকরণ থেকে পাই ,

p(x+y) = 2pq

বা, x+y = 2pq /p

বা, x+y = 2q

বা, x = 2q –y —(iii)

(iii) নং সমীকরণ থেকে প্রাপ্ত x এর মান (ii) নং সমীকরণে x-এর পরিবর্তে বসিয়ে পাই ,

q(x-y) = 2pq

বা, q (2q-y-y) = 2pq

বা, q(2q-2y) = 2pq

বা, 2q (q-y) = 2pq

বা, q-y = p

বা, y = q-p

y-এর প্রাপ্ত মান (iii) নং সমিকরণে বসিয়ে পাই ,

 x = 2q –y

বা, x = 2q – (q-p)

বা, x = 2q-q+p

বা,  x = q+p

∴ নির্ণেয় সমাধান x = p+q এবং y =  q-p

WBBSE Class 9 Math Koshe Dekhi 5.5|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) কষে দেখি 5.5|পরিবর্ত পদ্ধতি

গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।

ধন্যবাদ । এই POST টি ভালো লাগলে SHARE করার অনুরোধ রইল । এই রকম আরও সুন্দর সুন্দর POST পেতে , আমাদের FACEBOOK PAGE টি LIKE করুন ।