WBBSE Class 9 Math Koshe Dekhi 5.7.রৈখিক সহ সমীকরণ(দুই চল বিশিষ্ট )কষে দেখি -5.7

WBBSE Class 9 Math Koshe Dekhi 5.7.রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7।কষে দেখি ৫.৭।গণিত প্রকাশ ক্লাস ৯ (নবম শ্রেণি )(ক্লাস IX) সমাধান। Gonit Prokash Class 9 Math Solution Of Chapter 5 Exercise 5.7.Simultaneous Linear Equation Of Two Variable.

গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।

WBBSE OFFICIAL SITE

গণিত প্রকাশ দশম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।

WBBSE Class 9 Math Koshe Dekhi 5.7.রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7।কষে দেখি ৫.৭।গণিত প্রকাশ ক্লাস ৯ (নবম শ্রেণি )(ক্লাস IX) সমাধান। Gonit Prokash Class 9 Math Solution Of Chapter 5 Exercise 5.7.Simultaneous Linear Equation Of Two Variable.

Koshe Dekhi-5.7|কষে দেখি 5.7

1. আমাদের স্কুলের পাশের বইয়ের দোকান থেকে আমার বন্ধু  রীতা 34 টাকায় 5 টি পেন ও 3 টি পেন্সিল কিনেছে । কিন্তু সুমিত ওই দোকান থেকে একই দামে 7 টি পেন ও 6 টি পেনসিল 53 টাকায় কিনেছে । আমি সহসমীকরণ গঠন করে প্রতিটি পেন ও প্রতিটি পেনসিলের দাম হিসাব করে লিখি ।

সমাধানঃ ধরি ,  একটি পেনের দাম x টাকা এবং একটি পেনসিলের দাম y টাকা ।

∴ 5 টি পেন ও 3 টি পেনসিলের  মোট দাম = (5x +3y ) টাকা এবং 7 টি পেন ও 6 টি পেনসিলের মোট দাম = (7x+6y) টাকা ।

শর্তানুসারে ,

5x+3y = 34 —(i)

এবং , 7x+6y = 53 —(ii)

(i) নং সমীকরণে 2 দ্বারা এবং (ii) নং সমীকরণকে 1 দ্বারা গুণ করে পাই ,

10x + 6y = 68 —(iii)

এবং , 7x +6y = 53 —(iv)

(iii) নং ও (iv)নং সমীকরণদ্বয় বিয়োগ করে পাই ,

(10x+6y) – (7x+6y) = 68-53

বা, 10x +6y -7x -6y = 15

বা, 3x= 15

বা, x = 15/3

বা,x = 5

X –এর মান (i) নং সমীকরণে বসিয়ে পাই ,

5x+3y = 34

বা, 5(5) +3y = 34

বা, 25+3y = 34

বা, 3y = 34 -25

বা, 3y = 9

বা, y = 9/3

বা, y = 3

∴নির্নেয় সমাধান x = 5 ,y = 3

∴ একটি পেনের দাম 5 টাকা এবং একটি পেনসিলের দাম 3 টাকা ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

2. আমার বন্ধু আয়েশা ও রফিকের ওজন একত্রে 85 কিগ্রা. । আয়েশার ওজনের অর্ধেক রফিকের ওজনের 4/9 অংশের সমান হলে , সহসমীকরণ  গঠন করে তাদের পৃথকভাবে ওজন হিসাব করে লিখি ।

সমাধানঃ ধরি , আয়েশার  ওজন x কিগ্রা এবং রফিকের ওজন y কিগ্রা ।

শর্তানুসারে ,

x+y = 85 —(i)

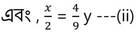
(i) নং সমীকরণ থেকে পাই ,

x = 85 –y —(iii)

(ii) নং সমীকরণ থেকে পাই ,

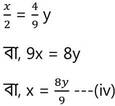
(iii) নং ও (iv) নং সমীকরণ থেকে প্রাপ্ত x –এর মানের তুলনা করে পাই,

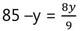
বা, 9 (85 –y) = 8y

বা,  765 – 9y = 8y

বা, 8y +9y = 765

বা , 17y = 765

বা, y = 765 /17

বা, y = 45

Y –এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই ,

x = 85 –y

বা, x = 85 -45

বা, x = 40

∴নির্ণেয় সমাধান x = 40 , y = 45

∴ আয়েশার ওজন 40 কিগ্রা এবং রফিকের ওজন 45 কিগ্রা ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

3. আমার কাকাবাবুর বর্তমান বয়স আমার বোনের বর্তমান বয়সের দ্বিগুন । 10 বছর আগে আমার কাকাবাবুর বয়স আমার বোনের বয়সের তিনগুন ছিল । সমীকরণ গঠন করে তাদের বর্তমান বয়স পৃথক ভাবে হিসাব করে লিখি ।

সমাধানঃ ধরি , আমার বোনের বর্তমান বয়স x বছর এবং কাকাবাবুর বর্তমান বয়স y বছর ।

∴10 বছর আগে বোনের বয়স ছিল (x-10) বছর এবং কাকাবাবুর বয়স (y -10 ) বছর ।

শর্তানুসারে ,

y = 2x —(i)

এবং , y -10 = 3(x-10)  —(ii)

(i) নং সমীকরণ থেকে প্রাপ্ত y –এর মান (ii) নং সমীকরণে y –এর পরিবর্তে বসিয়ে পাই ,

y -10 = 3(x-10) 

বা, 2x – 10 = 3x – 30

বা, 2x -3x = 10 -30

বা, -x = -20

বা, x = 20

x –এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই ,

y = 2x

বা, y = 2(20 )

বা, y = 40

∴ নির্ণেয় সমাধান x = 20 ,y = 40

∴ বোনের বর্তমান বয়স 20 বছর এবং কাকাবাবুর বর্তমান বয়স 40 বছর ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

4. আমাদের গ্রামের দেবকুমার কাকু 590 টাকার একটি চেক ভাঙালেন । যদি তিনি ব্যাঙ্ক থেকে পাঁচ টাকার ও দশ টাকার নোট মোট 70 খানা পেয়ে থাকেন , তবে তিনি ব্যাঙ্ক থেকে কতগুলি পাঁচ টাকার নোট এবং কতগুলি দশ টাকার নোট পেলেন হিসাব করে লিখি ।

সমাধানঃ ধরি , পাঁচ টাকার নোটের সংখ্যা x টি এবং দশ টাকার নোটের সংখ্যা y টি ।

শর্তানুসারে ,

 x + y = 70 —(i)

5x+10y = 590 —(ii)

(i) নং সমীকরণকে 10 দ্বারা গুণ করে (ii) নং সমীকরণ থেকে বিয়োগ করে পাই ,

(10x+10y) – (5x+ 10y) = 700 – 590

বা, 10x +10y -5x -10y = 110

বা, 5x = 110

বা, x = 22

X –এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই ,

22+y = 70

বা, y = 70 – 22

বা, y = 48

∴ পাঁচ টাকার নোটের সংখ্যা 22 টি এবং দশ টাকার নোটের সংখ্যা 48 টি ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

5. আমাদের স্কুলের ব্ল্যাকবোর্ডে এমন একটি প্রকৃত ভগ্নাংশ লিখব যার হরটি লব অপেক্ষা 5 বেশি এবং লব ও হরের সঙ্গে যদি 3 যোগ করি তবে ভগ্নাংশটি ¾ হবে । সমীকরণ গঠন করি ও সমাধান করে প্রকৃত ভগ্নাংশটি ব্ল্যাকবোর্ডে লিখি ।

সমাধানঃ ধরি , ভগ্নানাংশটি হল – x/y  । অর্থাৎ x হল লব এবং y হল হর যেখানে (x < y)

শর্তানুসারে ,

y = x+5 —-(i)

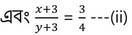
(ii) নং সমীকরণ থেকে পাই ,

4 (x+3) = 3(y+3)

বা, 4x +12 = 3y +9

বা, 4x -3y = -12 +9

বা, 4x -3y = -3

বা, -3y = -4x -3

বা, 3y = 4x +3

বা, y = (4x+3) /3 —(iii)

(i) নং ও (iii) নং সমীকরণ থেকে প্রাপ্ত y এর মান তুলনা করে পাই ,

X+5 = (4x+3) /3

বা, 3(x+5) = 4x +3

বা, 3x+15 = 4x + 3

বা, 3x-4x = -15 + 3

বা, -x = – 12

বা, x = 12

X –এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই ,

y = x+5

বা, y = 12+5

বা, y = 17

∴ ভগ্নাংশটি হল = 12/17

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

6. মারিয়া তার খাতায় দুটি এমন সংখ্যা লিখেছে যে প্রথম সংখ্যার সঙ্গে 21 যোগ করলে তা দ্বিতীয় সংখ্যার দ্বিগুন হয় । আবার দ্বিতীয় সংখ্যার  সঙ্গে 12 যোগ করলে  তা প্রথম সংখ্যার দ্বিগুন হয় । হিসাব করে মারিয়ার লেখা সংখ্যাদুটি লিখি ।

সমাধানঃ ধরি , মারিয়ার লেখা দুটি সংখ্যা হল x এবং y ।

শর্তানুসারে ,

x +21 = 2y —(i)

এবং , y+12 = 2x —(ii)

(i) নং সমীকরণ থেকে পাই ,

X -2y = -21 —(iii)

(ii) নং সমীকরণ থেকে পাই ,

-2x +y  = -12 —(iv)

(iii) নং সমীকরণকে 2 দ্বারা গুণ করে (iv) নং সমীকরণের সাথে যোগ করে পাই ,

(2x – 4y) + (-2x+y)  = -42 + (-12)

বা, 2x -4y -2x +y = -42 – 12

বা, -3y = -54

বা, y = -54 / -3

বা, y = 18

 y –এর প্রাপ্ত মান (i)নং সমীকরণে বসিয়ে পাই ,

x +21 = 2y

বা, x + 21 = 2(18)

বা, x+21 = 36

বা, x = 36-21

বা, x = 15  

∴ মারিয়ার লেখা সংখ্যা দুটি হল  15 এবং 18 ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

7. লালিমা ও রমেন দুজনেই তাদের বাড়ির বাগান পরিস্কার করে । লালিমা 4 দিনে ও রমেন 3 দিনে একসঙ্গে বাগান পরিস্কার করলে কাজটির 2/3 অংশ সম্পন্ন হয় । আবার লালিমা 3 দিন ও রমেন 6 দিনে একসঙ্গে বাগান  পরিস্কার করলে কাজটির 11 /12 অংশ সম্পন্ন হয়  । সহ সমীকরণ গঠন করি এবং সমাধান করে লালিমা ও রমেন পৃথক ভাবে কাজটি করলে কতদিনে শেষ করবে হিসাব করে লিখি ।

সমাধানঃ ধরি , লালিমা এবং রমেন পৃথকভাবে যথাক্রমে  x দিনে ও y দিনে কাজটি সম্পন্ন করবে ।

∴ লালিমা x দিনে কাজ করে 1 অংশ

    লালিমা 1 দিনে কাজ করে 1/x অংশ

   লালিমা  4 দিনে কাজ করে 4/x অংশ

এবং , রমেন y দিনে কাজ করে 1 অংশ

         রমেন 1 দিনে কাজ করে 1/y অংশ

     ∴ রমেন 3 দিনে কাজ করে 3/y অংশ

আবার ,  লালিমা x দিনে কাজ করে 1 অংশ

    লালিমা 1 দিনে কাজ করে 1/x অংশ

   লালিমা  3 দিনে কাজ করে 3/x অংশ

এবং , রমেন y দিনে কাজ করে 1 অংশ

         রমেন 1 দিনে কাজ করে 1/y অংশ

     ∴ রমেন 6 দিনে কাজ করে 6/y অংশ

শর্তানুসারে ,

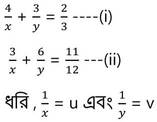
∴ (i)নং ও (ii) নং সমীকরণ থেকে পাই ,

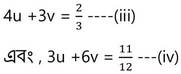
(iii) নং সমীকরণ থেকে পাই ,

3(4u +3v) = 2

বা, 12 u +9v = 2

বা, 12u = 2 -9v

(v) ও (vi) নং সমীকরণ থেকে প্রাপ্ত x –এর মানের তুলনা করে পাই ,

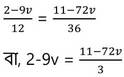
বা, 3 (2-9v) = 11-72v

বা, 6 – 27v = 11-72v

বা, 72v -27v = 11 – 6

বা,  45v = 5

বা , v = 5/45

বা, v = 1/9

V –এর মান (v) নং সমীকরণে বসিয়ে পাই ,

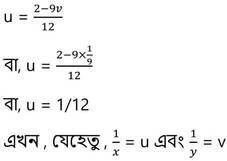
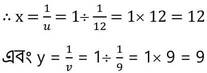
∴ লালিমা  কাজটি  একা করে 12 দিনে এবং রমেন কাজটি একা সম্পন্ন করে 9 দিনে ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

8. আমার মা দুধরনের শরবত তৈরি করেছেন । প্রথম  ধরনের 100 লিটার শরবতে 5 কিগ্রা. চিনি এবং দ্বিতীয় ধরনের 100 লিটার শরবতে 8 কিগ্রা চিনি আছে । আমি দুধরনের শরবত মিশিয়ে 150 লিটার শরবত  তৈরি করব , যাতে চিনির পরিমাণ থাকবে  9 পূর্ণ 2/3 কিগ্রা  । সহসমীকরণ গঠন করে হিসাব করে দেখি 150 লিটার শরবতে দুধরনের শরবত কতটা পরিমাণ থাকবে ?

সমাধানঃ ধরি , 150 লিটার শরবতে দুধরণের শরবতের পরিমাণ যথাক্রমে x লিটার এবং y লিটার । 

∴ x+y = 150 —(i)

প্রথম ধরনের ,

100 লিটার শরবতে চিনির পরিমাণ 5 কিগ্রা.

1   লিটার শরবতে চিনির পরিমাণ 5/100 কিগ্রা

x   লিটার শরবতে চিনির পরিমাণ 5x /100 কিগ্রা.

দ্বিতীয় ধরনের,

100 লিটার শরবতে চিনির পরিমাণ 8 কিগ্রা.

1 লিটার শরবতে চিনির  পরিমাণ 8 /100 কিগ্রা.

y লিটার শরবতে চিনির পরিমাণ 8y/ 100 কিগ্রা.

শর্তানুসারে ,

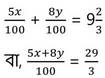
বা, 15x +24y = 2900 —(iii)

(i) নং সমীকরণকে 24 দ্বারা গুণ করে পাই ,

24x+24y = 3600 —(iv)

(iv) নং সমীকরণ থেকে (iii) নং সমীকরণ বিয়োগ করে পাই ,

24x+24y-15x-24y = 3600 -2900

বা, 9x = 700

বা, x = 700/9

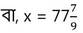
x –এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই ,

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

9.গত বছর বকুলতলা গ্রাম পঞ্চায়েত নির্বাচনে অখিলবাবু ও ছন্দাদেবী প্রার্থী ছিলেন । অখিলাবু ছন্দাদেবীকে 75 টি ভোটে পরাজিত করলেন । অখিলবাবু কে যারা ভোট দিয়েছেন তাদের 20 % যদি ছন্দাদেবীকে ভোট দিতেন , তাহলে ছন্দাদেবী 19 টি ভোটে জিততে পারতেন । সহসমীকরণ  গঠন করে সমাধান করে দেখি ,কে কত ভোট পেয়েছেন ?

সমাধানঃ ধরি , অখিল বাবুকে ভোট দিয়েছেন x জন এবং ছন্দা দেবী কে ভোট দিয়েছেন y জন ।

এখন , অখিলাবু ছন্দাদেবীকে 75 টি ভোটে পরাজিত করলেন ।

∴ x –y = 75 —-(i)

আবার, অখিলবাবু কে যারা ভোট দিয়েছেন তাদের 20 % যদি ছন্দাদেবীকে ভোট দিতেন , তাহলে ছন্দাদেবী 19 টি ভোটে জিততে পারতেন ।

(i) নং সমীকরণকে  5 দ্বারা গুণ করে পাই ,

5x – 5y = 375 —-(iv)

(iii) নং ও (iv) নং সমীকরণ যোগ করে পাই ,

5y -3x +5x -5y = 95+375

বা, 2x = 470

বা, x = 235

x-এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই ,

x – y = 75

বা, 235 – y = 75

বা, y = 235 -75

বা, y = 160

∴ অখিল বাবুর প্রাপ্ত ভোটের সংখ্যা 235 টি এবং ছন্দা দেবীর প্রাপ্ত ভোটের সংখ্যা 160 টি ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।

10. রফিকদের আয়তক্ষেত্রাকার মেঝের দৈর্ঘ্য 2 মিটার এবং প্রস্থ 3 মিটার বৃদ্ধি করলে ক্ষেত্রফল 75 বর্গমিটার বৃদ্ধি পায় । কিন্তু দৈর্ঘ্য 2 মিটার হ্রাস এবং প্রস্থ 3 মিটার বৃদ্ধি করলে ক্ষেত্রফল 15 বর্গমিটার বৃদ্ধি পায় । সহ-সমীকরণ গঠন করে  রফিকদের মেঝের দৈর্ঘ্য ও প্রস্থ নির্ণয় করি ।

সমাধানঃ ধরি , রফিকদের আয়তক্ষেত্রাকার মেঝের দৈর্ঘ্য x মিটার এবং প্রস্থ y মিটার ।  

∴আয়তক্ষেত্রাকার মেঝের ক্ষেত্রফল xy বর্গমিটার ।

মেঝের দৈর্ঘ্য 2 মিটার এবং প্রস্থ 3 মিটার বৃদ্ধি করলে , মেঝের ক্ষেত্রফল হয় = (x+2)(y+3) বর্গমিটার । এবং , মেঝের দৈর্ঘ্য 2 মিটার হ্রাস এবং প্রস্থ 3 মিটার বৃদ্ধি করলে মেঝের ক্ষেত্রফল হয় = (x-2)(y+3) বর্গমিটার ।

শর্তানুসারে ,

∴ (x+2)(y+3) –xy = 75 —-(i)

∴ (x-2)(y+3) –xy = 15 —(ii)

(i) নং সমীকরণ থেকে পাই ,

(x+2)(y+3) –xy = 75

বা, xy +2y+3x +6 –xy = 75

বা, 3x +2y = 75-6

বা, 3x +2y = 69 —(iii)

(ii) নং সমীকরণ থেকে পাই ,

xy -2y+3x-6 –xy = 15

বা, 3x -2y = 15+6

বা, 3x -2y = 21 —(iv)

(iii) নং ও (iv) নং সমীকরণ যোগ করে পাই ,

3x+2y +3x-2y = 69+21

বা, 6x = 90

বা, x = 90/6

বা, x = 15

x-এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই ,

3(15) +2y = 69

বা, 45 +2y = 69

বা, 2y = 69-45

বা, 2y =  24

বা, y = 24/2

বা, y = 12

∴ আয়তক্ষেত্রাকার মেঝের দৈর্ঘ্য 15 মিটার এবং প্রস্থ 12 মিটার ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

11. আমার বন্ধু মেরি ঈশানকে বলল , তোমার  টাকার 1/3 অংশ আমায় দাও তাহলে আমার 200 টাকা হবে । ঈশান মেরিকে বলল , তোমার টাকার অর্ধেক আমাকে দিলে আমার 200 টাকা হবে । সহসমিকরণ গঠন করে হিসাব করে দেখি কার কাছে কত টাকা আছে ?

সমাধানঃ ধরি , মেরির কাছে x টাকা এবং ঈশানের কাছে y টাকা আছে ।

শর্তানুসারে ,

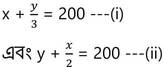
(i) নং সমীকরণ থেকে পাই ,

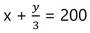
বা, 3x+y = 600 —(iii)

(iii) নং সমীকরণকে 3 দ্বারা গুণ করে (iv) নং সমীকরণ থেকে বিয়োগ করে পাই ,

(6x + 2y) –(2y+x) = 1200 – 400

বা, 6x +3y -3y –x = 800

বা, 5x = 800

বা, x = 800 /5

বা, x = 160

x –এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই ,

3(160) +y = 600

বা, 480 +y = 600

বা, y = 600 -480

বা, y = 120

∴ মেরির কাছে 160 টাকা এবং  ঈশানের কাছে 120 টাকা ছিল ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

12. আজ আমার দাদা ও তার কিছু বন্ধুরা একসঙ্গে মেলায় যাবে । তাই আমার দাদু তাদের মধ্যে কিছু টাকা সমান ভাগে ভাগ করে দিলেন । দেখছি , যদি 2 জন বন্ধু কম থাকত তবে প্রত্যেকে 18 টাকা পেত । আবার যদি 3 জন বন্ধু বেশি থাকত তবে প্রত্যেকে 12 টাকা পেত । দাদারা কত জন মেলায় গেছিল এবং দাদু মোট কত টাকা তাদের মধ্যে সমান ভাগে ভাগ করে দিয়েছিলেন হিসাব করে লিখি ।

সমাধানঃ ধরি , দাদারা x জন বন্ধু ছিল  এবং দাদু y টাকা তাদের মধ্যে সমান ভাগে ভাগ করে দিয়েছিলেন ।

শর্তানুসারে ,

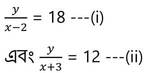
(i) নং সমীকরণ থেকে পাই ,

y = 18x -36

বা, y – 18x = -36 —(iii)

(ii) নং সমীকরণ থেকে পাই ,

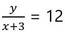
বা, y = 12x +36

বা, y – 12x = 36 —(iv)

(iii) নং ও (iv) নং সমীকরণ বিয়োগ করে পাই ,

(y -18 x) – (y-12x) = -36 -36

বা, y -18x –y +12x = -72

বা, -6x = -72

বা, x = -72 /-6

বা, x = 12

x-এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই ,

y – 18x = -36

বা, y – 18(12) = -36

বা, y – 216 = -36

বা, y = 216 – 36

বা, y =  180

∴ দাদারা 12 জন বন্ধুমিলে মেলায় গেছিল এবং দাদু তাদের 180 টাকা দিয়েছিলেন ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

13. আমার দাদার একটি থলিতে 1 টাকার মুদ্রা ও 50 পয়সার মুদ্রা মিলিয়ে 350 টাকা আছে । আমার বোন ওই টাকার থলি থেকে এক তৃতীয়াংশ 50 পয়সা বের করে তার জায়গায় সমসংখ্যক 1 টাকার মুদ্রা রেখে দিল এবং ওই থলিতে মোট টাকার পরিমাণ 400 টাকা হল । প্রথমে দাদার থলিতে আলাদা ভাবে 1 টাকার মুদ্রা ও 50 পয়সার মুদ্রা কতগুলো ছিল  হিসাব করে লিখি ।

সমাধানঃ ধরি , দাদার থলিতে 1 টাকার মুদ্রার সংখ্যা x টি এবং 50 পয়সার মুদ্রার সংখ্যা y টি ।

∴ 1 টাকার মুদ্রার সংখ্যা 200 টি এবং 50 পয়সার মুদ্রার সংখ্যা 300 টি ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

14. আজ মামার বাড়ি যাব । তাই একটি মোটর গাড়ি আমাদের বাড়ি থেকে সমবেগে মামার বাড়ির দিকে রওনা দিল । যদি গাড়িটির গতিবেগ ঘণ্টায় 9 কিমি. বেশি হতো তবে ওই পথ অতিক্রম করতে 3 ঘণ্টা সময় কম লাগত । আবার গতিবেগ যদি ঘণ্টায় 6 কিমি. কম হতো তবে ওই পথ অতিক্রম করতে তার 3 ঘণ্টা সময় বেশি লাগত । আমাদের বাড়ি থেকে মামার বাড়ির দূরত্ব এবং গাড়ির গতিবেগ ঘণ্টায় কত কিমি. ছিল  হিসাব করে লিখি ।

সমাধানঃ ধরি , আমার বাড়ি থেকে মামার বাড়ির দূরত্ব x কিমি এবং মোটর গাড়ির গতিবেগ y কিমি / ঘণ্টা ।

∴ আমার বাড়ি থেকে মামার বাড়ির দূরত্ব 540 মিটার এবং মোটর গাড়ির গতিবেগ 36 কিমি. / ঘণ্টা ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

15. মোহিত এমন একটি দুই অঙ্কের সংখ্যা লিখবে যেটি তার অঙ্কদ্বয়ের সমষ্টির 4 গুণ অপেক্ষা 3 বেশি । এবং সংখ্যাটির অঙ্কদ্বয় স্থান বিনিময় করলে যে সংখ্যা হয় তা মূল সংখ্যার চেয়ে 18 বেশি ।  হিসাব করে দেখি মোহিত কোন সংখ্যা লিখবে ?

সমাধানঃ ধরি , মোহিতের লেখা সংখ্যার এককের অঙ্ক x এবং দশকের অঙ্ক y । 

∴ সংখ্যাটি হল – 10y +x

অঙ্কদ্বয় স্থান বিনিময় করলে যে সংখ্যা হয় তা হল – 10x+y

শর্তানুসারে ,

10y +x = 4(x+y)+3 —(i)

এবং , (10x+y) –(10y+x) = 18 —(ii)

(i) নং সমীকরণ থেকে পাই ,

 10y +x = 4(x+y)+3

বা, 10y +x = 4x+4y +3

বা, 10y +x – 4x -4y = 3

বা, 6y -3x = 3

বা, 2y –x = 1 —(iii)

(ii) নং সমীকরণ থেকে পাই ,

(10x+y) –(10y+x) = 18

বা, 10x+y -10y –x = 18

বা, 9x -9y = 18

বা, x-y = 2 —(iv)

(iii) নং ও (iv) নং সমীকরণ যোগ করে পাই ,

(2y-x) + (x-y) = 1+2

বা, 2y –x + x – y = 3

বা, y = 3

y –এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই ,

2(3) –x = 1

বা, 6 –x = 1

বা, x = 6-1

বা, x = 5

∴ নির্ণেয় সংখ্যাটি হল – 10 y+x =10(3) +5 = 35

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

16. আমি একটি দুই অঙ্কের সংখ্যা লিখব যার অঙ্কদুটির সমষ্টি 14 এবং সংখ্যাটি থেকে 29 বিয়োগ করলে অঙ্কদুটি সমান হবে । সমীকরণ গঠন করি ও সমধান করে দেখি দুই অঙ্কের সংখ্যাটি কী হবে ।

সমাধানঃ ধরি , দুই অঙ্কের সংখ্যার এককের ঘরের অঙ্ক x এবং দশকের ঘরের অঙ্ক y ।

∴ সংখ্যাটি হবে (10y+x) 

দুই অঙ্কের সংখ্যাটির যার অঙ্কদুটির সমষ্টি 14

∴ x+y = 14 —(i)

আবার , সংখ্যাটি থেকে 29 বিয়োগ করলে নতুন সংখ্যাটি হয় –

 = (10y+x) – 29

= 10y +x-29

= 10y+x -30 +1

= 10(y-3) +(x+1)

আবার , সংখ্যাটি থেকে 29 বিয়োগ অঙ্কদুটি সমান হবে

∴ y-3 = x+1

বা, y -x = 3+1

বা, y-x = 4 —(ii)

(i) নং ও (ii) নং সমীকরণ যোগ করে পাই ,

X +y +y-x = 14 +4

বা, 2y = 18

বা, y = 18/2

বা, y = 9

y-এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই ,

x+y = 14

বা, x + 9 =14

বা, x = 5

∴ সংখ্যাটি হবে (10y+x) =  {10(9)+5} = 95 ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.

17. রহমত চাচা তার নৌকা নিয়ে স্রোতের অনুকূলে 6 ঘণ্টায় 30 মাইল গিয়ে এই পথ স্রোতের প্রতিকূলে 10 ঘণ্টায় ফিরে এলেন । স্থির জলে রহমত চাচার নৌকার গতিবেগ ও স্রোতের গতিবেগ হিসাব করে লিখি ।

সমাধানঃ ধরি , নৌকার গতিবেগ xকিমি. / ঘণ্টা এবং স্রোতের গতিবেগ y কিমি. / ঘণ্টা ।

স্রোতের অনুকূলে নৌকার বেগ = (x+y) কিমি. / ঘণ্টা এবং স্রোতের প্রতিকূলে নৌকার বেগ (x-y) কিমি. / ঘণ্টা ।

∴ স্রোতের অনুকূলে নৌকাটি 30 মাইল অতিক্রম করতে সময় লাগবে 30 /(x+y) ঘণ্টা । [যেহেতু , সময় = দূরত্ব / গতিবেগ ]

এবং , স্রোতের প্রতিকূলে নৌকাটি 30 মাইল অতিক্রম করতে সময় লাগবে 30 /(x- y) ঘণ্টা । [যেহেতু , সময় = দূরত্ব / গতিবেগ ]

শর্তানুসারে ,

বা, x-y = 30/10

বা, x-y = 3 —(iv)

(iii) নং ও (iv) নং সমীকরণ যোগ করে পাই ,

x+y +x-y = 5+3

বা, 2x = 8

বা, x = 8/2

বা, x = 4

x –এর  প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই ,

4 +y = 5

বা, y = 5-4

বা, y = 1

∴ স্থির জলে নৌকার বেগ 4 মাইল / ঘণ্টা এবং স্রোতের বেগ 1 মাইল / ঘণ্টা ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।

18. হাওড়া স্টেশন থেকে একটি ট্রেন ছাড়ার 1 ঘণ্টা পরে বিশেষ কারণে 1 ঘণ্টা দেরি করে এবং তারপর পূর্বের বেগের 3/5 অংশ বেগে চলে নির্দিস্ট সময়ের 3 ঘণ্টা পরে গন্তব্য স্থলে  পৌঁছায়  । যদি বিশেষ কারণটি পুর্বস্থান থেকে আরও 50 কিমি. দুরবর্তী স্থানে হত ,তাহলে ট্রেনটি আগের চেয়ে 1 ঘণ্টা 20 মিনিট পূর্বে গন্তব্য স্থলে পৌঁছাত । ট্রেনটি মোট কত পথ চলেছিল এবং পূর্বের বেগ কত ছিল হিসাব করে লিখি ।

সমাধানঃ ধরি , ট্রেনটির গতিবেগ ছিল ঘণ্টায়  x কিমি এবং ট্রেনটি y ঘণ্টায় গন্তব্য স্থলে পৌঁছায় ।

∴ গন্তব্যস্থলের দূরত্ব xy কিমি. ।

প্রথম 1 ঘণ্টায় ট্রেনটি যায় x কিমি ।

∴ অবশিষ্ট পথ = (xy –x) কিমি.

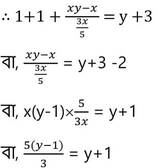
বা, 5y-5 = 3y+3

বা, 5y -3y = 5+3

বা, 2y = 8

বা, y = 8/2

বা, y = 4 —(i)

50 কিমি দূরবর্তী স্থানে যদি বিশেষ কারণটি হতো , তখন স্থানটির দূরত্ব হত (x +50) কিমি. ।

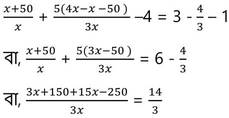
বা, 18x – 100 = 14x

বা, 18x-14x = 100

বা, 4x = 100

বা, x = 100/4

বা, x = 25

∴ ট্রেনটি মোট পথ চলেছিল xy কিমি. =  (25✕4 )কিমি. = 100 কিমি. এবং ট্রেনটির গতিবেগ ছিল ঘণ্টায় 25 কিমি.।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

19. মৌসুমি দুই অঙ্কের একটি সংখ্যাকে অঙ্কদুটির সমষ্টি দিয়ে ভাগ ভাগফল 6 এবং ভাগশেষ 6 পায় । যদি মৌসুমি অঙ্ক দুটি স্থান বিনিময় করে সংখ্যাটিকে অঙ্কদুটির সমষ্টি দিয়ে ভাগ করে তাহলে ভাগফল 4 এবং ভাগশেষ 9 হয় । সহ সমীকরণ গঠন করে মৌসুমির সংখ্যাটি লেখো ।

সমাধানঃ ধরি , মৌসুমির লেখা সংখ্যাটির এককের ঘরের অঙ্ক x এবং দশকের ঘরের অঙ্ক y ।

∴ সংখ্যাটি হল (10y+x )

অঙ্কদ্বয় স্থান পরিবর্তন করে লিখলে সংখ্যাটি হবে – (10x+y)

দুই অঙ্কের একটি সংখ্যাকে অঙ্কদুটির সমষ্টি দিয়ে ভাগ ভাগফল 6 এবং ভাগশেষ 6

∴ 10y+x = 6(x+y) +6 —(i) [যেহেতু, ভাজ্য = ভাজক ✕ ভাগফল +ভাগশেষ ]

আবার , 10x+y = 4(x+y)+9 —(ii) [যেহেতু, ভাজ্য = ভাজক ✕ ভাগফল +ভাগশেষ ]

(i) নং সমীকরণ থেকে পাই ,

10y+x = 6x+6y +6

বা, 10y+x -6x-6y = 6

বা, 4y -5x =6 —(iii)

(ii) নং সমীকরণ থেকে পাই ,

10x+y = 4(x+y)+9

বা, 10x +y -4x -4y = 9

বা, 6x -3y = 9

বা, 2x – y = 3 —- (iv)

(iv) নং সমীকরণকে 4 দ্বারা গুণ করে পাই ,

8x – 4y = 12 —(v) 

(iii) নং ও (v) নং সমীকরণদ্বয়কে যোগ করে পাই ,

4y -5x +8x -4y = 6 +12

বা, 3x = 18

বা, x = 18/3

বা, x = 6

x –এর মান (iv) নং সমীকরণে বসিয়ে পাই ,

2(6) –y = 3

বা, 12 –y = 3

বা, y = 12- 3

বা, y = 9

∴ সংখ্যাটি হল (10y+x) =10 (9) + 6 = 96 ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

20. ফরিদাবিবি কয়েকটি বাক্সে কমলালেবু রাখতে গিয়ে দেখলেন যে তিনি যদি প্রত্যেকটি বাক্সে 20 টি কমলালেবু বেশি রাখেন তাহলে 3 টি বাক্স কম লাগে । আবার তিনি যদি প্রত্যেকটি বাক্সে 5 টি কমলালেবু কম রাখেন তাহলে 1 টি বাক্স বেশি লাগে । সহসমীকরণ গঠন করে হিসাব করি ফরিদাবিবির কাছে কতগুলি কমলালেবু এবং কতগুলি বাক্স ছিল ।

শর্তানুসারে ,

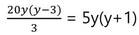
বা, 20y – 60 = 15y +15 [যেহেতু , y ¹ 0 , উভয়পক্ষে y দ্বারা ভাগ করে পাই ]

বা, 20y -15y = 60+15

বা, 5 y = 75

বা, y = 75/5

বা, y = 15

y-এর প্রাপ্ত মান (iv) নং সমীকরণে বসিয়ে পাই ,

x = 5y(y+1)

বা, x = 5.15(15+1)

বা, x =  75. 16

বা, x = 1200

∴ ফরিদাবিবির কাছে কমলালেবুর সংখ্যা 1200 টি এবং বাক্সের সংখ্যা 15 টি ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

21. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ

(i) যদি x= 3t এবং y = 2t/3 -1 হয় , তাহলে t –এর কোন মানের জন্য x =3y হবে ?

সমাধানঃ যেহেতু , x =3y

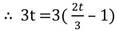
বা, 3t = 2t -3

বা, 3t -2t = -3

বা, t = -3

∴ t = -3 হলে x = 3y হবে ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

(ii) K –এর কোন মানের জন্য 2x+5y =8 এবং 2x-ky =3 সমীকরণদ্বয়ের কোনো সমাধান থাকবে না ?

সমাধানঃ প্রদত্ত সমীকরণদ্বয়ের কোনো সমাধান থাকবে না যদি , x –এর সহগ দ্বয়ের অনুপাত = y-এর সহগ দ্বয়ের অনুপাত ≠ধ্রুবক পদের অনুপাত হয় ।

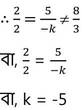
∴ k = -5 হলে , 2x+5y =8 এবং 2x-ky =3 সমীকরণদ্বয়ের কোনো সমাধান থাকবে না ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

(iii) x ,y বাস্তব সংখ্যা এবং (x -5)² +(x-y)² = 0 হলে , x এবং y এর মান কত ?

সমাধানঃ  (x -5)² +(x-y)² = 0

এক্ষেত্রে , দুটি বর্গ রাশির যোগফল শূন্য অতএব তারা আলাদা আলাদা ভাবে শূন্য ।

∴ x -5 =0

বা, x = 5

এবং x –y = 0

বা, x = y

∴ x=y = 5

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

(iv) x² +y² -2x+4y = -5 হলে , x এবং y –এর মান কত ?

সমাধানঃ x² +y² -2x+4y = -5

বা, x2 +y2 -2x+4y +5 =0

বা, x² -2x +1 +y² +4y +4 =0

বা, (x-1)² +(y+2)² = 0

এক্ষেত্রে দুটি বর্গ রাশির যোগফল শূন্য অতএব তারা আলাদা আলাদা ভাবে শূন্য ।

∴ x -1 =0

বা, x =1

এবং , y+2 =0

বা, y = -2

∴ x = 1 , y =-2

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

(v) r এর কোন মানের জন্য rx -3y -1 = 0 এবং (4-r)x-y +1 = 0 সমীকরণদ্বয়ের সমাধান সম্ভব নয়  ।

সমাধানঃ প্রদত্ত সমীকরণদ্বয়ের কোনো সমাধান থাকবে না যদি , x –এর সহগ দ্বয়ের অনুপাত = y-এর সহগ দ্বয়ের অনুপাত ≠ ধ্রুবক পদের অনুপাত হয় ।

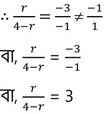
বা, r = 3(4-r)

বা, r = 12 -3r

বা, r+3r = 12

বা, 4r = 12

বা, r = 12/4

বা, r = 3

∴ r = 3 হলে rx -3y -1 = 0 এবং (4-r)x-y +1 = 0 সমীকরণদ্বয়ের সমাধান সম্ভব নয়  ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।

(vi) a₁x+b₁y+c₁ = 0 সমীকরণকে y = mx+c আকারে লিখি , যেখানে m ও c ধ্রুবক ।

সমাধানঃ

a₁x+b₁y+c₁ = 0

বা, b₁y = -a₁x –c₁

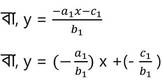
WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

(vii) k –এর কোন মানের জন্য kx -21y +15 = 0 এবং 8x-7y = 0 সমীকরণ দ্বয়ের একটি মাত্র সমাধান থাকবে ?

সমাধানঃ প্রদত্ত সমীকরণ দ্বয়ের অসংখ্য সমাধান থাকবে যদি , x –এর সহগদ্বয়ের অনুপাত ¹ y –এর সহগ দ্বয়ের অনুপাত ।

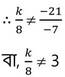
, k ≠ 24

∴ k ≠ 24 হলে kx -21y +15 = 0 এবং 8x-7y = 0 সমীকরণ দ্বয়ের একটি মাত্র সমাধান থাকবে ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

(viii) a ও b এর কোন মানের জন্য 5x+8y = 7 এবং (a+b)x +(a-b)y = (2a+b+1) সমীকরণ দ্বয়ের অসংখ্য সমাধান থাকবে ।

সমাধানঃ প্রদত্ত সমীকরণদ্বয়ের অসংখ্য সমাধান থাকবে যদি , X –এর সহগ দ্বয়ের অনুপাত = y-এর সহগ দ্বয়ের অনুপাত = ধ্রুবক পদের অনুপাত হয় ।

∴  a +b = 5k —(i)

এবং , a –b = 8k —(ii)

এবং , 2a +b +1 = 7k —(iii)

(i) ও (ii) যোগ করে পাই ,

a+b +a-b = 13k

বা, 2a = 13k

বা, a = 13k/2

আবার , (i) ও (ii) বিয়োগ করে পাই ,

a+b –a+b = -3k

বা , 2b = -3k

বা, b = -3k/2

(iii) নং সমীকরণ থেকে পাই ,

2a +b +1 = 7k

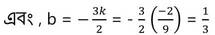
∴ a-এর মান – 13/9 এবং b -এর মান 1/3 ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

22. বহু বিকল্পীয় প্রশ্ন  (M.C.Q):

(i) 4x+3y =7 এবং 7x-3y = 4 সমীকরণদ্বয়ের

(a) একটি নির্দিস্ট সমাধান আছে ।

(b) অসংখ্য সমধান আছে ।

(c ) কোনো সমাধান নেই ।

(d) কোনোটিই নয়

Ans: (a) একটি নির্দিস্ট সমাধান আছে ।

সমাধানঃ  4x+3y =7 এবং 7x-3y = 4 সমীকরণদ্বয়ের

x –এর সহগদ্বয়ের অনুপাত = 4/7

y –এর সহগদ্বয়ের অনুপাত = 3/-3

∴ x –এর সহগদ্বয়ের অনুপাত ≠ y –এর সহগদ্বয়ের অনুপাত

প্রদত্ত সমীকরণদ্বয়ের একটি নির্দিস্ট সমাধান আছে ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

(ii) 3x+6y = 15 এবং 6x+ 12y = 30 সমীকরণদ্বয়ের

(a) একটি নির্দিস্ট সমাধান আছে ।

(b) অসংখ্য সমধান আছে ।

(c ) কোনো সমাধান নেই ।

(d) কোনোটিই নয়

Ans: (b) অসংখ্য সমধান আছে ।

সমাধানঃ

x –এর সহগদ্বয়ের অনুপাত = 3/6 = 1/2

 y –এর সহগদ্বয়ের অনুপাত = 6/12 = ½

এবং , ধ্রুবক পদের অনুপাত = 15 /30 = ½

∴ x –এর সহগদ্বয়ের অনুপাত = y –এর সহগদ্বয়ের অনুপাত = ধ্রুবক পদের অনুপাত

∴ প্রদত্ত সমীকরণ দ্বয়ের অসংখ্য সমাধান আছে ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

(iii) 4x+4y =20 এবং 5x+5y = 30 সমীকরণদ্বয়ের

(a) একটি নির্দিস্ট সমাধান আছে ।

(b) অসংখ্য সমধান আছে ।

(c ) কোনো সমাধান নেই ।

(d) কোনোটিই নয়

Ans: (c ) কোনো সমাধান নেই ।

সমাধানঃ x –এর সহগদ্বয়ের অনুপাত = 4/5

 y –এর সহগদ্বয়ের অনুপাত = 4/5

এবং , ধ্রুবক পদের অনুপাত = 20/30 = 2/3

∴ x –এর সহগদ্বয়ের অনুপাত = y –এর সহগদ্বয়ের অনুপাত ≠ ধ্রুবক পদের অনুপাত

প্রদত্ত সমীকরণদ্বয়ের কোনো সমাধান নেই ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

(iv) নিম্নলিখিত সমীকরণগুলির মধ্যে কোনটির সমাধান (1,1)

(a) 2x+3y = 9

(b) 6x+2y =9

(c ) 3x+2y = 5

(d) 4x+6y = 8

Ans: (c ) 3x+2y = 5

সমাধানঃ 3x+2y =3 (1)+2(1) = 3+2 =5

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

(v) 4x+3y =25 এবং 5x -2y = 14 সমীকরণদ্বয়ের সমাধান

(a) x =4 ,y=3

(b) x =3 ,y =4

(c ) x =3 ,y =3

(d) x =4 , y =-3

Ans: (a) x =4 ,y=3

সমাধানঃ একমাত্র ,  x =4 ,y=3 মানগুলি প্রদত্ত সমীকরণদ্বয়কে সিদ্ধ করে ।

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

(vi) x +y = 7 সমীকরণের সমাধানগুলি হলো

(a) (1,6) , (3,-4)

(b) (1,-6) , (4,3)

(c ) (1,6),(4,3)

(d) (-1,6) , (-4,3)

Ans: (c ) (1,6),(4,3)

সমাধানঃ  x =1 ,y=6 এবং x = 4 এবং y = 3 ,এই মানগুলিই শুধুমাত্র  প্রদত্ত সমীকরণটিকে সিদ্ধ করে ।

1+6 = 7 এবং 4 +3 = 7

WBBSE Class 9 Math Koshe Dekhi 5.7|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট ) কষে দেখি -5.7

গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।

ধন্যবাদ । এই POST টি আপনাদের ভালো লাগলে SHARE করার অনুরোধ রইল । এইরকম আরও সুন্দর সুন্দর POST পেতে , আমেদের FACEBOOK PAGE টি LIKE করুন ।