WBBSE Class 9 Math Koshe Dekhi 5.3|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) কষে দেখি ৫.৩।গণিত প্রকাশ ক্লাস ৯ কষে দেখি ৫.৩।গনিত প্রকাশ নবম শ্রেণি কষে দেখি ৫.৩। অপনয়ন পদ্ধতি। Ganit Prakash Class 9 Math Koshe Dekhi 5.3.
গণিত প্রকাশ নবম শ্রেণির সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
WBBSE Class 9 Math Koshe Dekhi 5.3|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) কষে দেখি ৫.৩|গণিত প্রকাশ ক্লাস ৯ কষে দেখি ৫.৩|গনিত প্রকাশ নবম শ্রেণি কষে দেখি ৫.৩|অপনয়ন পদ্ধতি|Gonit Prokash Class 9 Math Koshe Dekhi 5.3.
1. নীচের দুইচল বিশিষ্ট একঘাত সহসমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি ও লেখচিত্রের সাহায্যে সমাধান করে যাচাই করি:
(a) 8x+5y-11=0 , 3x-4y-10 = 0
সমাধানঃ প্রদত্ত সহসমীকরণ দুটি হল –
8x+5y-11=0 —(i) এবং 3x-4y-10 = 0 —(ii)
এখন , (i) নং সমীকরণকে 4 দ্বারা এবং (ii) নং সমীকরণকে 5 দ্বারা গুণ করে পাই ,
32x+20y-44 = 0 —(iii)
15x -20y -50 = 0 —(iv)
(iii) নং ও (iv) নং সমীকরণ যোগ করে পাই ,
32x+20y-44+15x -20y -50 = 0
বা, 47x – 94 =0
বা, 47x = 94
বা, x = 94/47
বা, x = 2
x –এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই ,
8(2)+5y-11 = 0
বা, 16+5y-11= 0
বা, 5y + 5 = 0
বা, 5y = -5
বা, y = -5/5
বা, y = -1
∴ নির্ণেয় সমাধান x = 2 এবং y = -1
লেখচিত্রের সাহায্যে সমাধানঃ
8x+5y-11 = 0
বা, x = (11-5y) / 8
| X | -3 | 2 | 7 |
| y | 7 | -1 | -9 |
3x-4y-10 = 0
বা, x = (10+4y) /3
| X | 6 | 10 | 2 |
| y | 2 | 5 | -1 |
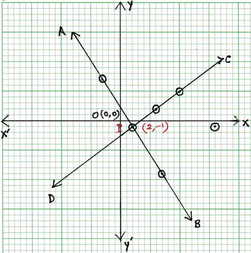
ছক কাগজে XOX এবং YOY দুটি পরপর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের একটি বাহুকে 1 একক ধরে (-3,7) ,(2,-1) এবং (7,-9) বিন্দুগুলি স্থাপন করে ও যোগ করে AB সরলরেখা এবং (6,2) ,(10,5) ,(2,-1) বিন্দুগুলি যোগ করে CD সরলরেখা অঙ্কন করলাম । AB ও CD সরলরেখা পরস্পর P বিন্দুতে ছেদ করে । P বিন্দুর স্থানাঙ্ক (2,-1) । সুতরাং নির্ণেয় সমাধান x=2 , y =-1
অর্থাৎ অপনয়ন পদ্ধতিতে সহসমীকরণ দুটির সমাধান এবং লেখচিত্রের মাধ্যমে নির্ণেয় সমাধান সমান ।
গণিত প্রকাশ নবম শ্রেণির সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
(b) 2x+3y-7=0 , 3x+2y -8 = 0
সমাধানঃ প্রদত্ত সহ সমীকরণ দুটি হল –
2x+3y-7=0 —(i)
3x+2y -8 = 0 —(ii)
(i) নং সমীকরণকে 2 দ্বারা এবং (ii) নং সমীকরণকে 3 দ্বারা গুণ করে পাই ,
4x + 6y -14 = 0 —(iii)
9x +6y – 24 = 0 —(iv)
এখন ,(iii) নং ও (iv) নং সমীকরণকে বিয়োগ করে পাই ,
(4x+6y-14) –(9x+6y-24) = 0
বা, 4x + 6y -14 – 9x -6y +24 = 0
বা, -5x +10 = 0
বা, 5x = 10
বা, x = 10 /5
বা, x = 2
X এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই ,
2 (2) +3y -7 = 0
বা, 4 + 3y -7 = 0
বা, 3y -3 =0
বা, 3y = 3
বা, y = 3/3
বা, y = 1
∴ নির্নেয় সমাধান x = 2 এবং y =1
লেখচিত্রের সাহায্যে সমাধানঃ
2x+3y-7=0
বা, 2x = 7-3y
বা, x = (7-3y) /2
| X | 2 | -1 | 5 |
| y | 1 | 3 | -1 |
3x+2y -8 = 0
বা, x = (8-2y) /3
| x | 0 | -2 | -4 |
| y | 4 | 7 | 10 |
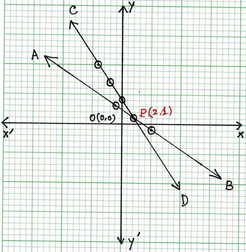
ছক কাগজে XOX এবং YOY দুটি পরপর লম্ব অক্ষ অঙ্কন করে ও প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের একটি বাহুকে 1 একক ধরে (2,1) ,(-1,3) এবং (5,-1) বিন্দুগুলি স্থাপন করে ও যোগ করে AB সরলরেখা এবং (0,4) ,(-2,7) ,(-4,10) বিন্দুগুলি যোগ করে CD সরলরেখা অঙ্কন করলাম । AB ও CD সরলরেখা পরস্পর P বিন্দুতে ছেদ করে । P বিন্দুর স্থানাঙ্ক (2,1) । সুতরাং নির্ণেয় সমাধান x=2 , y =1।
অর্থাৎ অপনয়ন পদ্ধতিতে সহসমীকরণ দুটির সমাধান এবং লেখচিত্রের মাধ্যমে নির্ণেয় সমাধান সমান ।
2. 7x-5y+2 = 0 সমীকরণকে কত দিয়ে গুণ করে 2x+15y+3 = 0 সমীকরণের সঙ্গে যোগ করব যাতে y চলটিকে অপনিত করতে পারি ।
সমাধানঃ
7x-5y+2 = 0 —(i)
2x+15y+3 = 0 —(ii)
5 এবং 15 এর লসাগু 15 অর্থাৎ y –কে অপনীত করতে গেলে (i) নং সমীকরণকে 3 দ্বারা গুণ করতে হবে ।
3. 4x-3y = 16 ও 6x+5y = 62 উভয় সমীকরণকে সবথেকে ছোটো কোন স্বাভাবিক সংখ্যা দিয়ে গুণ করলে দুটি সমীকরণের x – এর সহগ সমান হবে তা লিখি ।
সমাধানঃ
4x-3y = 16 —(i)
6x+5y = 62 —(ii)
(i) নং ও (ii) নং সমীকরণে x এর সহগ যথাক্রমে 4 ও 6
4 ও 6 এর লসাগু – 12
∴ (i) নং সমীকরণকে 3 দ্বারা ও (ii) নং সমীকরণকে 2 দ্বারা গুণ করলে সমীকরণদ্বয়ের x – এর সহগ সমান হবে ।
4. নীচের দুইচল বিশিষ্ট সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি ।
(i) 3x+2y = 6 , 2x -3y = 17
সমাধানঃ প্রদত্ত সহ-সমীকরণদ্বয় হল –
3x+2y = 6 —(i)
, 2x -3y = 17 —(ii)
(i) নং সমীকরণকে 3 দ্বারা এবং (ii) নং সমীকরণকে 2 দ্বারা গুণ করে পাই ,
9x + 6y = 18 —(iii)
এবং 4x – 6y = 34 —(iv)
এখন (iii) ও (iv) নং সমীকরণ যোগ করে পাই ,
9x + 6y +4x – 6y = 18+34
বা, 13x = 52
বা, x = 52 /13
বা, x = 4
X এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই ,
3x+2y = 6
বা, 3(4) +2y = 6
বা, 12 + 2y = 6
বা, 2y = 6 -12
বা, 2y = -6
বা, y = -6/2
বা, y = -3
∴নির্ণেয় সমাধান x = 4 এবং y = -3 ।
(ii) 2x+3y = 32 , 11y-9x = 3
সমাধানঃ প্রদত্ত সহ-সমীকরণদ্বয় হল –
2x+3y = 32 —(i)
11y-9x = 3 —(ii)
(i) নং সমীকরণকে 9 দ্বারা এবং (ii) নং সমীকরণকে 2 দ্বারা গুণ করে পাই ,
18x + 27y = 288 —(iii)
22y – 18x = 6 —(iv)
(iii) নং ও (iv) নং সমীকরন যোগ করে পাই ,
18x +27y + 22y -18x = 288 +6
বা, 49y = 294
বা, y = 294 / 49
বা, y = 6
Y এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই ,
2x+3(6) = 32
বা, 2x + 18 = 32
বা, 2x = 32-18
বা, 2x = 14
বা, x = 14/2
বা, x = 7
∴ নির্ণেয় সমাধান x = 7 এবং y = 6 ।
(iii) x+y = 48 , x+4 = 5/2 (y+4)
সমাধানঃ প্রদত্ত সহ-সমীকরণদ্বয় হল –
x+y = 48 —(i)
x+4 = 5/2 (y+4) —(ii)
(ii) নং সমীকরণ থেকে পাই ,
2(x+4) = 5(y+4)
বা, 2x+8 = 5y+20
বা, 2x-5y = 20-8
বা, 2x-5y = 12 —(iii)
(i) নং সমীকরণকে 5 দ্বারা এবং (iii) নং সমীকরণকে 1 দ্বারা গুণ করে পাই ,
5x+5y = 240 —-(iv)
2x-5y = 12 —(v)
এখন , (iv) নং ও (v) নং সমীকরণ যোগ করে পাই ,
5x+5y+2x-5y =240+12
বা, 7x = 252
বা, x = 252/ 7
বা, x = 36
X এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই ,
36 + y = 48
বা, y = 48-36
বা, y = 12
∴ নির্ণেয় সমাধান x = 36 এবং y = 12 ।

(iii) নং সমীকরণকে 6 দ্বারা এবং (iv) নং সমীকরণকে 1 দ্বারা গুণ করে পাই ,
18x+12y = 288 —(v)
এবং , 5x-12y = -12 —(vi)
(v) ও (vi) নং সমীকরণকে যোগ করে পাই ,
18x+12y +5x-12y = 288-12
বা, 23x = 276
বা, x = 276 /23
বা, x = 12
X এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই ,
3x+2y = 48
বা, 3(12) +2y = 48
বা, 36+2y =48
বা, 2y = 48-36
বা, 2y = 12
বা, y = 12/2
বা, y = 6
∴ নির্ণেয় সমাধান x = 12 এবং y = 6

বা, y = 2
∴ নির্ণেয় সমাধান x =2 এবং y =2

বা, 2x+3y = 6 —(iv)
(iii) নং সমীকরণকে 3দ্বারা এবং (iv) নং সমীকরণকে 2 দ্বারা গুণ করে পাই ,
9x+6y = 18 —(v)
এবং 4x+6y = 12 —(vi)
(v) ও(vi) নং সমীকরণকে বিয়োগ করে পাই ,
(9x+6y) – (4x+6y) = 18-12
বা, 9x+6y -4x-6y = 6
বা, 5x = 6
বা, x = 6/5




বা, 9x+7y = 126 —(iv)
(iii) নং সমীকরণকে 7 দ্বারা ও (iv) নং সমীকরণকে 3 দ্বারা গুণ করে পাই ,
35x-21y = 56 —(v)
27x + 21y = 378—(vi)
(v) নং ও (vi) নং সমীকরণ যোগ করে পাই ,
35x-21y + 27x + 21y = 56+378
বা, 62x = 434
বা, x = 434 /62
বা, x = 7
x এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই ,
5(7) -3y = 8
বা, 35 -3y = 8
বা, 35 – 8 =3y
বা, 3y = 27
বা, y = 27/3
বা, y = 9
∴ নির্ণেয় সমাধান x = 7 এবং y = 9


গণিত প্রকাশ নবম শ্রেণির সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
WBBSE Class 9 Math Koshe Dekhi 5.3|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) কষে দেখি ৫.৩|গণিত প্রকাশ ক্লাস ৯ কষে দেখি ৫.৩|গনিত প্রকাশ নবম শ্রেণি কষে দেখি ৫.৩|Gonit Prokash Class 9 Math Koshe Dekhi 5.3.


WBBSE Class 9 Math Koshe Dekhi 5.3|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) কষে দেখি ৫.৩|গণিত প্রকাশ ক্লাস ৯ কষে দেখি ৫.৩|গনিত প্রকাশ নবম শ্রেণি কষে দেখি ৫.৩|Gonit Prokash Class 9 Math Koshe Dekhi 5.3.

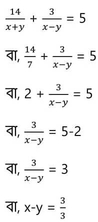
বা, x-y = 1 —(v)
(iv) নং ও (v) নং সমীকরণ যোগ করে পাই ,
x+y +x-y = 7+1
বা, 2x = 8
বা, x = 8/2
বা, x = 4
X এর প্রাপ্ত মান (iv) নং সমীকরণে বসিয়ে পাই ,
4+y = 7
বা, y = 7-4
বা, y = 3
∴ নির্ণেয় সমাধান x = 4 এবং y = 3
WBBSE Class 9 Math Koshe Dekhi 5.3|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) কষে দেখি ৫.৩|গণিত প্রকাশ ক্লাস ৯ কষে দেখি ৫.৩|গনিত প্রকাশ নবম শ্রেণি কষে দেখি ৫.৩|Gonit Prokash Class 9 Math Koshe Dekhi 5.3.


বা, 2x+2y-3x+3y +5=0
বা, 5y –x = -5 —(iv)
(iii) নং ও (iv) নং সমীকরণ বিয়োগ করে পাই ,
(9y-x)- (5y-x) = 7-(-5)
বা, 9y –x -5y +x = 7+5
বা, 4y = 12
বা, y = 12/4
বা, y = 3
Y –এর প্রাপ্ত মান (iii) নং সমীকরনে বসিয়ে পাই ,
9y-x =7
বা, 9(3) – x =7
বা, 27- x = 7
বা, x = 27-7
বা, x = 20
∴ নির্ণেয় সমাধান x = 20 এবং y = 3
WBBSE Class 9 Math Koshe Dekhi 5.3|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) কষে দেখি ৫.৩|গণিত প্রকাশ ক্লাস ৯ কষে দেখি ৫.৩|গনিত প্রকাশ নবম শ্রেণি কষে দেখি ৫.৩|Gonit Prokash Class 9 Math Koshe Dekhi 5.3.
(xii) x+y =a+b , ax-by =a2-b2
সমাধানঃ প্রদত্ত সহ-সমিকরণদ্বয় হল-
x+y =a+b —(i)
ax-by =a2-b2 —(ii)
(i) নং সমীকরণকে b দ্বারা গুণ করে পাই ,
bx –by = ab+b2 —(iii)
(ii) ও(iii) নং সমীকরণ যোগ করে পাই ,
ax-by +bx –by = a2-b2 + ab+b2
বা, ax+bx = a2+ab
বা, x(a+b) = a(a+b)
বা, x = a [ উভয়পক্ষে (a+b) দ্বারা ভাগ করে পাই ]
X এর প্রাপ্ত মাণ (i) নং সমীকরণে বসিয়ে পাই ,
x+y =a+b
বা, a+y =a+b
বা, y = a+b-a
বা, y = b
∴ নির্ণেয় সমাধান x = a এবং y = b
WBBSE Class 9 Math Koshe Dekhi 5.3|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) কষে দেখি ৫.৩|গণিত প্রকাশ ক্লাস ৯ কষে দেখি ৫.৩|গনিত প্রকাশ নবম শ্রেণি কষে দেখি ৫.৩|Gonit Prokash Class 9 Math Koshe Dekhi 5.3.

বা, b(x+a) = a(y+b)
বা, bx +ab = ay +ab
বা, bx –ay = 0 —(iii)
(ii) নং সমীকরণকে a দ্বারা এবং (iii) নং সমীকরণকে b দ্বারা গুণ করে পাই ,
a2x –aby = a3 –ab2 —(iv)
b2x –aby = 0 —(v)
(iv) ও (v) নং সমীকরণ বিয়োগ করে পাই ,
(a2x – aby) –(b2x –aby) = a3 –ab2
বা, a2x – aby– b2x +aby = a3 –ab2
বা, a2x – b2x = a(a2-b2)
বা, x(a2-b2) = a(a2-b2)
বা, x = a [ উভয়পক্ষে (a2-b2) দ্বারা ভাগ করে পাই ]
X এর প্রাপ্ত মান (iii) নং সমীকরণে বসিয়ে পাই ,
b(a) –ay = 0
বা, ab = ay
বা, y = b
∴ নির্ণেয় সমাধান x = a এবং y = b
WBBSE Class 9 Math Koshe Dekhi 5.3|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) কষে দেখি ৫.৩|গণিত প্রকাশ ক্লাস ৯ কষে দেখি ৫.৩|গনিত প্রকাশ নবম শ্রেণি কষে দেখি ৫.৩|Gonit Prokash Class 9 Math Koshe Dekhi 5.3.
(xiv) ax+by =c , a2x+b2y =c2
সমাধানঃ প্রদত্ত সহ-সমিকরণদ্বয় হল-
ax+by =c —(i)
a2x+b2y =c2 —(ii)
(i) নং সমীকরণকে b দ্বারা গুণ করে পাই ,
abx +b2y = bc —(iii)
(ii) নং ও (iii) নং সমীকরণ বিয়োগ করে পাই ,
(a2x+b2y)-( abx +b2y ) = c2 –bc
বা, a2x +b2y –abx-b2y = c2-bc
বা, a2x –abx = c2-bc
বা, ax (a-b) = c(c-b)
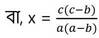
X –এর প্রাপ্ত মাণ (i) নং সমীকরণে বসিয়ে পাই ,
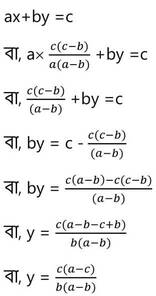
∴ নির্ণেয় সমাধান x = c(c-b)/a(a-b) এবং y =c(a-c) / b(a-b)
WBBSE Class 9 Math Koshe Dekhi 5.3|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) কষে দেখি ৫.৩|গণিত প্রকাশ ক্লাস ৯ কষে দেখি ৫.৩|গনিত প্রকাশ নবম শ্রেণি কষে দেখি ৫.৩|Gonit Prokash Class 9 Math Koshe Dekhi 5.3.


WBBSE Class 9 Math Koshe Dekhi 5.3|রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) কষে দেখি ৫.৩|গণিত প্রকাশ ক্লাস ৯ কষে দেখি ৫.৩|গনিত প্রকাশ নবম শ্রেণি কষে দেখি ৫.৩|Gonit Prokash Class 9 Math Koshe Dekhi 5.3.
(xvi) (7x-y-6) 2+(14x+2y-16)2 =0
সমাধানঃ প্রদত্ত সমীকরণটি হল – (7x-y-6) 2+(14x+2y-16)2 =0
দুটি বর্গ রাশির সমস্টি শূন্য
∴ তারা আলাদা আলাদা ভাবে শূন্য ।
∴ 7x-y -6 = 0 —(i)
এবং 14x+2y-16 = 0 —(ii)
(i) নং সমীকরণকে 2 দ্বারা গুণ করে পাই ,
14x -2y -12 = 0 —(iii)
(ii) নং ও (iii) নং সমীকরণ যোগ করে পাই ,
14x +2y -16 + 14x -2y -12 =0
বা, 28x -28 =0
বা, x = 28/28
বা, x = 1
X এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই ,
7(1) –y -6 = 0
বা, 7-6 –y =0
বা, 1 – y =0
বা, y =1
∴ নির্ণেয় সমাধান x = 1 এবং y =1
গণিত প্রকাশ নবম শ্রেণির সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
Thanks
Thanks
Thanks
Thanks☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺☺🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻❤❤❤❤❤❤❤❤❤