WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6|গণিত প্রকাশ নবম শ্রেণি (ক্লাস ৯) কষে দেখি ৬ সমাধান |Gonit Prokash Class 9 (IX) Exercise 6 Solution.
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
গণিত প্রকাশ দশম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
WBBSE Class 9 Math Koshe Dekhi 6.সামান্তরিকের ধর্ম কষে দেখি 6| গণিত প্রকাশ নবম শ্রেণি (ক্লাস ৯) কষে দেখি ৬ সমাধান|Gonit Prokash Class 9 (IX) Exercise 6 Solution.
কষে দেখি – 6
1. প্রমাণ করো যে, একটি সামান্তরিকের কর্ণদ্বয় সমান হলে সামান্তরিকটি একটি আয়তকার চিত্র ।

WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
2. প্রমাণ করি যে , একটি সামান্তরিকের কর্ণদ্বয়ের দৈর্ঘ্য সমান হলে এবং কর্ণদ্বয় পরপরকে লম্ব ভাবে ছেদ করলে , সামান্তরিকটি একটি বর্গাকার চিত্র ।

WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
3. প্রমাণ করি যে, একটি সামান্তরিকের কর্ণদ্বয় পরস্পরকে লম্ব ভাবে ছেদ করলে , প্রমাণ করো সামান্তরিকটি একটি রম্বস ।
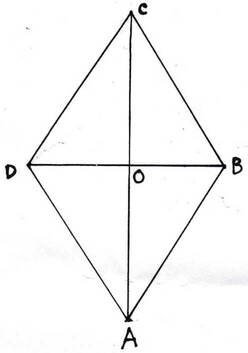
ধরা যাক , ABCD একটি সামান্তরিক যার AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে লম্ব ভাবে ছেদ করেছে ।
∴ ∠AOB =∠BOC =∠COD = ∠DOA = 90°
প্রমাণ করতে হবে যে , ABCD একটি রম্বস ।
প্রমাণঃ ∆AOB ও ∆BOC –এর মধ্যে ,
OB সাধারণ বাহু ।
∠AOB =∠BOC [ প্রত্যেকে 1 সমকোণ ]
এবং OA = OC [ যেহেতু সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে ]
∴ ∆BOC ≅ ∆BOA
∴ BC = AB
অনুরূপে প্রমাণ করা যায় ,BC =AD এবং AD = CD
∴ AB =BC =CD =DA
∴ ABCD সামান্তরিকের AB =BC =CD =DA
∴ ABCD একটি রম্বস ।
WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
4. ABCD সামান্তরিকের AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করেছে । O বিন্দুগামী যেকোনো সরলরেখা AB ও DC বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে । প্রমাণ করতে হবে OP =OQ
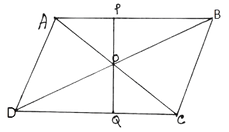
ABCD সামান্তরিকের AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করেছে ।O বিন্দুগামী একটি সরলরেখা AB ও DC বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে । প্রমাণ করতে হবে যে ,OP = OQ
প্রমাণঃ ∆AOP ও ∆COQ –এর মধ্যে ,
∠AOP = ∠COQ [ বিপ্রতীপ কোণ ]
OA = OC [ যেহেতু সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে ]
∠OAP = ∠OCQ [ একান্তর কোণ , যেহেতু ,AB||DC এবং AC ভেদক ]
∴ ∆AOP ≅ ∆COQ [কোণ –বাহু –কোণ শর্তানুসারে ]
∴ OP =OQ [প্রমাণিত ]
WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
5. প্রমাণ করি যে একটি সমদ্বিবাহু ট্রাপিজিয়ামের যেকোনো সমান্তরাল বাহু সংলগ্ন দুটি কোণ পরস্পর সমান ।
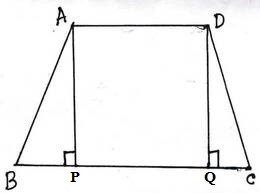
ধরা যাক ,ABCD একটি সমদ্বিবাহু ট্রাপিজিয়াম যার AD ||BC ,প্রমাণ করতে হবে যে , ∠ABC = ∠DCB
অঙ্কনঃ A ও D বিন্দু থেকে BC –এর ওপর যথাক্রমে AP ও DQ লম্ব অঙ্কন করা হল ।
প্রমাণঃ ∆APB ও ∆CQD –এর মধ্যে
∠APB = ∠DQC [ প্রত্যেকে 90° ]
AP =DQ [ যেহেতু , AD || BC এবং AP ও DQ উভয়েই BC-এর উপর লম্ব ]
AB = DC [কল্পনানুসারে ]
∴ APB ≅ CQB [R-H-S শর্তানুসারে ]
∴ ∠ABP = ∠DCQ
∴ ∠ABC = ∠DCB [প্রমাণিত ]
WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
6. ABCD বর্গাকার চিত্রের BC বাহুর উপর P যেকোনো একটি বিন্দু । B বিন্দু থেকে AP –এর উপর অঙ্কিত লম্ব DC বাহুকে Q বিন্দুতে ছেদ করেছে ।প্রমাণ করি যে , AP=BQ

WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
7. প্রমাণ করি যে ,একটি চতুর্ভুজের দুটি বিপরীত কোণ পরস্পর সমান ও দুটি বিপরীত বাহু পরস্পর সমান্তরাল হলে , চতুর্ভুজটি একটি সামান্তরিক ।

WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
8. ∆ABC-এর BP ও CQ মধ্যমা দুটি যথাক্রমে R ও S বিন্দু পর্যন্ত এমনভাবে বর্ধিত করা হল যে , BP =PR এবং CQ =QS হয় । প্রমাণ করি যে ,S ,A ,R বিন্দু তিনটি সমরেখ ।
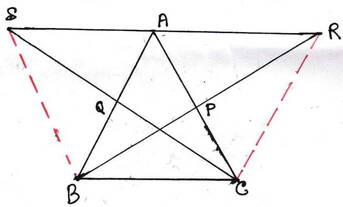
∆ABC –এর BP ও CQ মধ্যমা দুটি যথাক্রমে R ও S বিন্দু পর্যন্ত এমনভাবে বর্ধিত করা হল যে , BP =PR এবং CQ =QS হয় । প্রমাণ করতে হবে যে , S,A,R বিন্দু তিনটি সমরেখ ।
অঙ্কনঃ B,S ; C ,R যুক্ত করা হল ।
প্রমাণঃ ∆ABC ত্রিভুজের BP মধ্যমা ।
∴ AP=PC
আবার , BP =PR [ প্রদত্ত ]
∴ ABCR চতুর্ভুজের AC ও BR কর্ণদ্বয় পরস্পরকে P বিন্দুতে সমদ্বিখন্ডিত করে ।
∴ ABCR একটি সামান্তরিক ।
∴ AR ||BC [যেহেতু সামান্তরিকের বিপরীত বাহুগুলি পরস্পর সমান্তরাল ]
∴ ∠RAC = ∠ACB [একান্তর কোণ ]
ABC ত্রিভুজের CQ মধ্যমা ।
∴ AB বাহুর মধ্যবিন্দু Q
আবার , CQ =QS
∴ ACBS চতুর্ভুজের AB ও CS কর্ণদ্বয় Q বিন্দুতে পরস্পরকে সমদ্বিখন্ডিত করে ।
∴ ACBS একটি সামান্তরিক ।
∴ SA || BC [যেহেতু সামান্তরিকের বিপরীত বাহুগুলি পরস্পর সমান ]
∴ ∠SAB = ∠ABC [একান্তর কোণ ]
∆ABC এর
∠ABC+∠ACB = 180°-∠BAC
বা, ∠SAB +∠RAC = 180°-∠BAC
বা, ∠SAB +∠RAC +∠BAC = 180°
বা, ∠SAR = 180°
∴ S,A,R বিন্দু তিনটি সমরেখ ।
WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
9. PQRS সামান্তরিকের SQ কর্ণ K ও L বিন্দুতে সমান তিনভাগে বিভক্ত হয়েছে । PK,SR –কে M বিন্দুতে এবং RL,PQ-কে N বিন্দুতে ছেদ করেছে । প্রমাণ করি যে , PMRN একটি সামান্তরিক ।
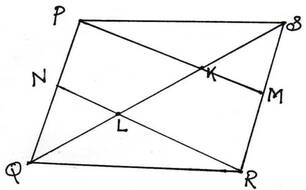
ধরা যাক , PQRS একটি সামান্তরিক । PQRS সামান্তরিকের SQ কর্ণ K ও L বিন্দুতে সমান তিনভাগে বিভক্ত হয়েছে ।
∴ SK = KL =LQ
আবার ,PK,SR –কে M বিন্দুতে এবং RL,PQ-কে N বিন্দুতে ছেদ করেছে । প্রমাণ করতে হবে যে, PMRN একটি সামান্তরিক ।
প্রমাণঃ ∆PKS এবং ∆QLR –এর ক্ষেত্রে ,
PS = QR [ সামান্তরিকের বিপরীত বাহু ]
SK = QL [ প্রদত্ত ]
∠LQR = ∠KSP [একান্তর কোণ , কারণ PS ||QR এবং QS ভেদক ]
∴ ∆PKS ≅ ∆QLR
∴ SPK = LRQ [ সর্বসম ত্রিভুজের অনুরূপ কোণ ]
আবার , ∆SPM এবং ∆QRN –এর ক্ষেত্রে ,
SP =QR [ সামান্তরিকের বিপরীত বাহু ]
∠SPM = ∠QRN [ পূর্বে প্রমাণিত ]
∠NQR = ∠MSP [ সামান্তরিকের বিপরীত কোণ ]
∴ ∆RNQ ≅ ∆SPM
∴ QN = SM [ সর্বসম ত্রিভুজের অনুরূপ বাহু ]
আবার , PQ =SR [ সামান্তরিকের বিপরীত বাহু ]
∴ PQ-QN = SR –SM
∴ PN = MR
আবার , PN || MR [ যেহেতু , PQ || SR ]
∴ PNRM চতুর্ভুজের একজোড়া বিপরীত বাহু (PN এবং RM) পরস্পর সমান ও সমান্তরাল ।
সুতরাং PNRM চতুর্ভুজটি একটি সামান্তরিক ।[প্রমাণিত ]
WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
10. ABCD ও AECF দুটি সামান্তরিকেরই AC একটি কর্ণ । B,E,D এবং F সমরেখ না হলে ,প্রমাণ করি যে , BEDF একটি সামান্তরিক ।
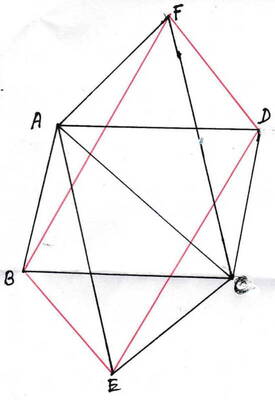
ধরা যাক , ABCD ও AECF দুটি সামান্তরিক । দুটি সামান্তরিকেরই AC একটি কর্ণ । B,E,D এবং F বিন্দুগুলি সমরেখ নয় । প্রমাণ করতে হবে যে , BEDF একটি সামান্তরিক ।
প্রমাণঃ ∆ABE এবং ∆CED এর মধ্যে ,
AB =CD [ABCD সামান্তরিকের বিপরীত বাহু ]—(i)
AF = EC [ AECF সামান্তরিকের বিপরীত বাহু ] —(ii)
আবার , ∠ACE = ∠CAF [একান্তর কোণ কারণ AF || FC এবং AC ভেদক ]
এবং ∠ACD = ∠BAC [ একান্তর কোণ কারণ AB || CD এবং AC ভেদক ]
∴ ∠ACE +∠ACD = ∠CAE +∠BAC
∴ ∠ECD =∠BAF —(iii)
(i) ,(ii) ও (iii) থেকে পাই ,
∆BAF ≅ ∆ECD
∴ BF = ED [সর্বসম ত্রিভুজের অনুরূপ বাহু ]
∆CDE এবং ∆ABF এর মধ্যে
CD = AB [ABCD সামান্তরিকের বিপরীত বাহু ]—(iv)
CF = AE [AECF সামান্তরিকের বিপরীত বাহু ] —(v)
এবং ∠BAC = ∠ACD [একান্তর কোণ কারণ AB||DC ,AC ভেদক ]
আবার , ∠EAC =∠ACF [একান্তর কোণ কারণ AE || FC ,AC ভেদক ]
∴ ∠BAC –∠EAC = ∠ACD – ∠ACF
∠BAF = ∠DCF —(iv)
∴ (iv) ,(v)এবং (vi) থেকে পাই ,
∆ABF ≅ ∆ECD
∴ BE =FD
∴ BEDF চতুর্ভুজের BF =ED এবং BE =FD ,অর্থাৎ একজোড়া বিপরীত বাহু সমান ।
∴ BEDF একটি সামান্তরিক ।[প্রমাণিত ]
WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
11. ABCD একটি চতুর্ভুজ । ABCE ও BADF দুটি সামান্তরিক অঙ্কন করা হলো । প্রমাণ করি যে , CD ও EF পরস্পরকে সমদ্বিখন্ডিত করে ।
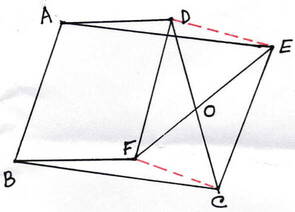
ABCD একটি চতুর্ভুজ । ABCE ও BADF দুটি সামান্তরিক। CD ও EF পরস্পরকে সমদ্বিখন্ডিত করে ।C ,D যুক্ত করাতে তা EF কে O বিন্দুতে ছেদ করল ।
প্রমাণ করতে হবে যে , CD ও EF পরস্পরকে O বিন্দুতে সমদ্বিখন্ডিত করে ।
অঙ্কনঃ D,E এবং C ,F যুক্ত করা হল ।
প্রমাণঃ ABCE একটি সামান্তরিক ।
∴ AB = CE এবং AB || CE —(i)
আবার , BADF একটি সামান্তরিক ।
∴ AB = DF এবং AB || DF —(ii)
(i) ও (ii) থেকে পাই ,
DF = EC এবং DF || EC
∴ DFCE চতুর্ভুজের একজোড়া বিপরীত বাহু পরস্পর সমান ও সমান্তরাল ।
∴ DFCE চতুর্ভুজটি একটি সামান্তরিক ।
আমরা জানি সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে ।
∴ CD ও EF পরস্পরকে O বিন্দুতে সমদ্বিখন্ডিত করেছে । [প্রমাণিত]
WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
12.ABCD সামান্তরিকের AB =2AD ; প্রমাণ করি যে , ∠BAD ও ∠ABC এর সমদ্বিখন্ডকদ্বয় DC বাহুর মধ্যবিন্দুতে সমকোণে মিলিত হয় ।
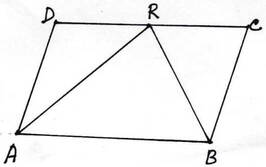
ABCD একটি সামান্তরিক যার, AB= 2AD ; প্রমাণ করতে হবে যে , ∠BAD ও ∠ABC এর সমদ্বিখন্ডকদ্বয় DC বাহুর মধ্যবিন্দুতে সমকোণে মিলিত হয় ।
প্রমাণঃ ABCD সামান্তরিকের DC || AB , AR ভেদক
∴ ∠ARD = ∠RAB [ একান্তর কোণ ]—(i)
আবার , AR হল কোণ ∠BAD এর সমদ্বিখন্ডক ।
∴ ∠DAR = ∠RAB —(ii)
(i) ও(ii)থেকে পাই ,
∠ARD = ∠DAR
∴ ∆ADR –এর AD = DR —(iii)
আবার AB = 2AD
বা, AD = ½ AB = ½ DC [ যেহেতু AB =DC (সামান্তরিকের বিপরীত বাহু ) ]
∴ DR = ½ DC [যেহেতু (iii) নং থেকে পাই AD =DR ]
∴ R ,DC এর মধ্যবিন্দু । —(iv)
আবার , ∠DAB+∠ABC =180° [ যেহেতু ভেদকের একই পার্স্বস্থ অন্তঃকোণের সমষ্টি 180° ]
বা, 2∠RAB +2∠RBA = 180° [ যেহেতু ,RA এবং RB যথাক্রমে BAD এবং ABC –এর সমদ্বিখণ্ডক ]
বা, 2(∠RAB +∠RBA) =180°
বা, ∠RAB +∠RBA = 180°/2
বা, ∠RAB +∠RBA = 90°
∴ ∆ABR –এর,
∠RAB +∠RBA+∠ARB =180°
বা, 90° + ∠ARB =180° [যেহেতু, ∠RAB +∠RBA = 90°]
বা, ∠ARB =180°-90°
বা, ∠ARB = 90° —(v)
∴(iv)ও (v) থেকে পাই , ∠BAD ও ∠ABC এর সমদ্বিখন্ডকদ্বয় DC বাহুর মধ্যবিন্দুতে সমকোণে মিলিত হয় । [ প্রমাণিত ]
WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
13. ABCD সামান্তরিকের AB ও AD বাহুর উপর যথাক্রমে ABPQ ও ADRS বর্গাকার চিত্র অঙ্কন করা হল যারা সামান্তরিকের বাইরে অবস্থিত । প্রমাণ করি যে , PRC ত্রিভুজটি সমদ্বিবাহু ।
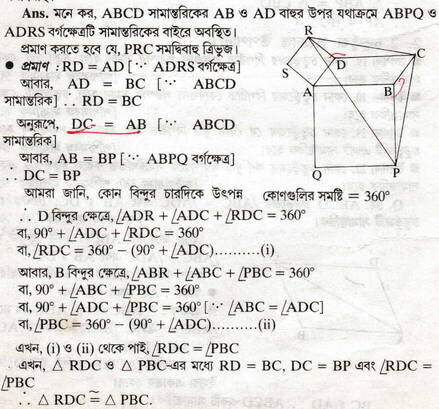
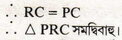
WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
14. ABCD সামান্তরিকের BAD স্থূলকোণ ; AB ও AD বাহুর উপর দুটি সমবাহু ত্রিভুজ ∆ABP ও ∆ADQ অঙ্কন করা হল যারা সামান্তরিকের বাইরে অবস্থিত । প্রমাণ করি যে , CPQ একটি সমবাহু ত্রিভুজ ।
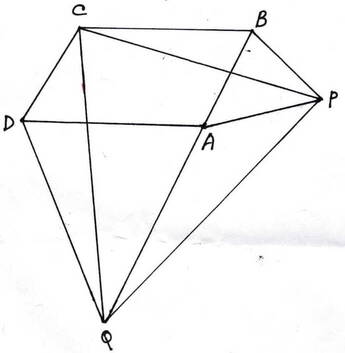
ABCD সামান্তরিকের ∠BAD স্থূলকোণ ; AB ও AD বাহুর উপর দুটি সমবাহু ত্রিভুজ ∆ABP ও ∆ADQ অঙ্কন করা হল যারা সামান্তরিকের বাইরে অবস্থিত । প্রমাণ করতে হবে যে , ∆CPQ একটি সমবাহু ত্রিভুজ ।
∆CDQ ও ∆CBQ –এর ,
CD = AB [ABCD সামান্তরিকের বিপরীত বাহু ] —(i)
DQ = AD [ যেহেতু , ∆ADQ সমবাহু ত্রিভুজ ]
আবার , AD = BC [ ABCD সামান্তরিকের বিপরীত বাহু ]
∴ DQ =BC —(ii)
∠ADQ = ∠ABP = 60°
এবং ∠ADC = ∠ABC [ABCD সামান্তরিকের বিপরীত কোণ ]
∴ ∠ADQ +∠ADC = ∠ABP+∠ABC
বা, ∠CQD = ∠PBC —(iii)
(i) ,(ii) ও (iii) থেকে পাই , ∆CQD ≅ ∆CBP
∴ CQ = CP [সর্বসম ত্রিভুজের অনুরূপ বাহু ] —(iv)
∠DAQ =∠BAP = 60° [যেহেতু , DAQ এবং BAP প্রত্যেকে সমবাহু ত্রিভুজ ]
∴ ∠BAD+∠PAQ =360° -120°
বা, ∠BAD +∠PAQ = 240°
বা, ∠PAQ = 240°-∠BAD
বা, ∠PAQ = 240°-(180 –∠ABC ) [যেহেতু , ABCD সামান্তরিকের ∠ABC+∠BAD = 180°]
বা , ∠PAQ = 240°-180+∠ABC
বা, ∠PAQ = 60°+∠ABC
বা , ∠PAQ =∠PBA +∠ABC [ যেহেতু , ∠PBA =60°]
বা, ∠PAQ = ∠PBC —(v)
AQ = AD [যেহেতু , ∆ADQ সমবাহু ত্রিভুজ ]
আবার , AD =BC [ সামান্তরিকের বিপরীত বাহু ]
∴ AQ = BC —(vi)
আবার , AP =PB [যেহেতু , ∆PAB সমবাহু ত্রিভুজ ] —(vii)
∴ (v) ,(vi) এবং (vii) থেকে পাই ,
∆PBC ≅ ∆AQP
∴ CP =PQ —(viii)
(iv)ও (viii)থেকে পাই ,
CQ = CP = PQ
∴ ∆PCQ একটি সমবাহু ত্রিভুজ ।
WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
15.OP ,OQ ও OR তিনটি সরলরেখাংশ । OPAQ ,OQBR এবং ORCP সামান্তরিক তিনটি অঙ্কন করা হল । প্রমাণ করতে হবে যে , AR ,BP ও CQ পরস্পরকে সমদ্বিখন্ডিত করে ।
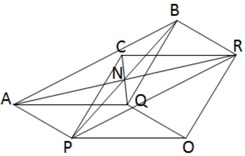
মনে করি , OP ,OR ও OQ তিনটি সরলরেখাংশ । OPAQ,OQBR এবং ORCP তিনটি সামান্তরিক অঙ্কন করা হয়েছে ।AR ,BP ও CQ সরলরেখা তিনটি পরস্পরকে N বিন্দুতে ছেদ করেছে ।প্রমাণ করতে হবে যে ,AR ,BP ও CQ সরলরেখা তিনটি পরস্পরকে সমদ্বিখন্ডিত করে ।
অঙ্কনঃ A,B এবং P,R যুক্ত করা হল ।
প্রমাণঃ যেহেতু , OAPQ একটি সামান্তরিক,
সুতরাং ,AP || QO এবং AP =QO
আবার যেহেতু OQBR একটি সামান্তরিক ,
সুতরাং ,OQ||BR এবং BR =QO
∴ AP || BR এবং AP =BR
∴ APRB একটি সামান্তরিক ,যার AR এবং BP দুটি কর্ণ ।
যেহেতু ,সামান্তরিকের কর্ণ পরস্পরকে সমদ্বিখন্ডিত করে ,সুতরাং AR ও BP সরলরেখা দুটি পরস্পরকে সমদ্বিখন্ডিত করে ।
∴ N, AR ও BP সরলরেখা দুটির মধ্যবিন্দু ।
এখন ∆AQN এবং ∆CRN এর মধ্যে
∠ANQ = বিপ্রতীপ ∠CNR এবং ∠AQN =একান্তর ∠NCR [ যেহেতু ,AQ||PO||CR]
এবং AN =NR
∴ ∆AQN ≅ ∆CRN
∴ NQ =CN [অনুরূপ বাহু ]
∴ N , CQ -এর মধ্যবিন্দু ।
∴ AR,BP ও CQ সরলরেখা তিনটি পরস্পরকে সমদ্বিখন্ডিত করে ।[প্রমাণিত]
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
16. বহু বিকল্পীয় প্রশ্ন (M.C.Q):
(i)ABCD সামান্তরিকের ∠BAD =75° এবং ∠CBD =60° হলে , ∠BDC –এর পরিমাপ
(a) 60°
(b) 75°
(c ) 45°
(d) 50°
Ans: (c ) 45°
সমাধানঃ
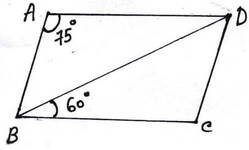
∠BAD = 75°
∴ ∠BCD = 75° [যেহেতু সামান্তরিকের বিপরীত বাহুগুলি পরস্পর সমান ]
এখন , BCD এর ,
∠BCD +∠CBD +∠BDC =180°
বা, 75° + 60° +∠BDC = 180°
বা, ∠BDC = 180° – 75°- 60°
বা, ∠BDC = 180° -135°
বা, ∠BDC = 45°
WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
(ii) নিম্নলিখিত জ্যামিতিক চিত্র গুলির মধ্যে কোনটির কর্ণ দ্বয়ের দৈর্ঘ্য সমান তা লিখি ।
(a) সামান্তরিক
(b) রম্বস
(c ) ট্রাপিজিয়াম
(d) আয়তকার চিত্র
Ans: (d) আয়তকার চিত্র
(iii) ABCD সামান্তরিকের ∠BAD = ∠ABC হলে , ABCD সামান্তরিকটি
(a) রম্বস
(b) ট্রাপিজিয়াম
(c ) আয়তকার চিত্র
(d) কোনোটিই নয়
Ans:(c ) আয়তকার চিত্র
সমাধানঃ ABCD সামান্তরিকের ∠BAD = ∠ABC
যেহেতু, ভেদকের একই পার্স্বস্থ অন্তঃস্থ কোণের সমষ্টি 180°
∴ ∠BAD + ∠ABC=180°
বা, ∠BAD +∠BAD = 180°
বা, 2∠BAD = 180°
বা, ∠BAD = 180°/2
বা, ∠BAD = 90°
∴ ABCD সামান্তরিকের একটি কোণের মান 90°
∴ ABCD একটি আয়তক্ষেত্র ।
WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
(iv) ABCD সামান্তরিকের BD কর্ণের মধ্যবিন্দু M ; BM ,∠ABC – কে সমদ্বিখন্ডিত করলে , ∠AMB এর পরিমাপ
(a) 45°
(b) 60°
(c ) 90°
(d) 75°
Ans: (c ) 90°
সমাধানঃ
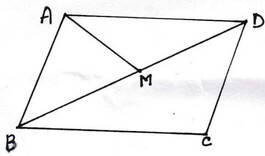
∠CBD = ∠ADB [একান্তর কোণ ]
আবার , ∠ABD = ∠CBD [যেহেতু , BD ,ABC এর সমদ্বিখন্ডক ]
∴ ∠ADB = ∠ABD
∴ AB =AD
∴ ABCD সামান্তরিকের AB = AD
∴ ABCD একটি রম্বস ।
যেহেতু , রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখন্ডিত করে ।
∴ ∠AMB = 90°
WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
(v) ABCD রম্বসের ∠ACB = 40° হলে , ∠ADB – এর পরিমাপ
(a) 50°
(b) 110°
(c ) 90°
(d) 120°
Ans: (a) 50°
সমাধানঃ
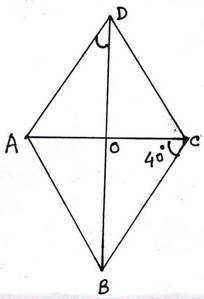
ABCD রম্বসের AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করেছে ।
∴ ∠AOD = 90°
∠ACB = 40°
∴ ∠ACB = ∠CAD =40° [একান্তর কোণ, যেহেতু , BC || AD এবং AC ভেদক ]
∆AOD এর ক্ষেত্রে ,
∠AOD +∠OAD +∠ODA = 180°
বা, 90°+40° +∠ODA = 180°
বা, ∠ODA = 180° -90°-40°
বা, ∠ODA = 50°
∴ ∠ADB= 50°
WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
17. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ
(i) ABCD সামান্তরিকের A :B = 3:2 হলে , সামান্তরিকটির কোণগুলির পরিমাপ লিখি ।
সমাধানঃ ধরি , A = 3x এবং B = 2x [x(≠0) একটি আনুপাতিক ধ্রুবক ]
ABCD সামান্তরিকের ,
∠A +∠B = 180° [যেহেতু , ভেদকের একই পার্স্বস্থ অন্তঃকোণের সমষ্টি 180° ]
বা, 3x+2x = 180°
বা, 5x =180°
বা, x = 180°/5
বা, x = 36°
∴ ∠A= 3✕36° = 108° এবং B = 2✕36° = 72°
যেহেতু, সামান্তরিকের বিপরীত কোণগুলির পরিমাপ সমান
∴ ∠C = 108° এবং ∠D = 72°
WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
(ii)ABCD সামান্তরিকের A ও B –এর সমদ্বিখন্ডকদ্বয় CD বাহুর উপর E বিন্দুতে মিলিত হয় । BC বাহুর দৈর্ঘ্য 2 সেমি. হলে , AB বাহুর দৈর্ঘ্য কত তা লিখি ।
সমাধানঃ
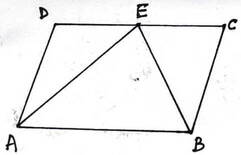
ABCD সামান্তরিকের ,
∠A ও ∠B কোণের সমদ্বিখন্ডকদ্বয় পরস্পর CD বাহুর উপর E বিন্দুতে মিলিত হয় ।
∴ ∠BAE = ∠DAE —(i)
এবং ∠BAE = ∠AED [একান্তর কোণ ] —(ii)
(i) ও (ii) থেকে পাই ,
∠DAE= ∠AED
∴ AD = DE
আবার , AD = DC =2 সেমি. [সামান্তরিকের বিপরীত বাহু ]
আবার , ∠ABE = ∠CBE [ যেহেতু , BE , ABC –এর সমদ্বিখন্ডক ]—(iii)
আবার , ∠ABE = ∠BEC [একান্তর কোণ ]—(iv)
(iii)ও (iv) থেকে পাই ,
∠CBE= ∠CBE
∴ CE = CB
∴CE = 2 সেমি.
∴ CD = CE +DE =( 2+2)সেমি.=4 সেমি.
∴ AB = 4 সেমি. [যেহেতু ,AB এবং CD পরস্পর ABCD সামান্তরিকের বিপরীত বাহু ]
WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
(iii) ABCD বর্গাকার চিত্রের ভিতর সমবাহু ত্রিভুজ ∆AOB অবস্থিত । ∠COD –এর পরিমাণ লিখি ।
সমাধানঃ
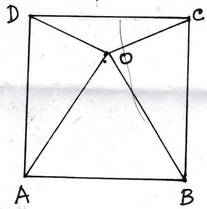
ABCD বর্গক্ষেত্রের ভিতরে ∆AOB সমবাহু ত্রিভুজ ।
∴ ∠AOB =∠OBA=∠OAB= 60°
∴ ∠OBC = 90°-∠OBA = 90°-60°=30°
এবং OA = AB =OB =BC
যেহেতু , OB = BC
∴ ∠BOC =∠BCO = (180°-∠OBC )/2 = (180°-30°)/2 = 150°/2 = 75°
অনুরূপে , ∠AOD = 75°
∴ ∠COD = 360°-(∠AOB+∠AOD+∠BOC) = 360°-(60°+75°+75°) = 180°-210° = 150°
WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
(iv) ABCD বর্গাকার চিত্রের AD বাহুর উপর M একটি বিন্দু যাতে ∠CMD = 30° হয় । কর্ণ BD , CM কে P বিন্দুতে ছেদ করলে , ∠DPC –এর পরিমাণ কত তা লিখি ।
সমাধানঃ
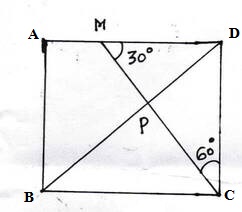
∠CMD = 30° [প্রদত্ত ]
∠CDM = 90°
∴ ∠MCD = 180° – (∠CMD+∠CDM)= 180° -(30°+90°) = 180° – 120° = 60°
আবার , ABCD বর্গক্ষেত্রের BD কর্ণ ।
∴ ∠BDC = ∠DBC = 45°
এখন , ∆CPD এর ক্ষেত্রে ,
∠CPD = 180° -(∠PCD + ∠PDC) = 180° -(60°+45°) =180° – 105° = 75°
WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
(v) ABCD রম্বসের AB বাহুর দৈর্ঘ্য 4 সেমি. এবং ∠BCD = 60° হলে , কর্ণ BD-এর দৈর্ঘ্য কত তা লিখি ।
সমাধানঃ
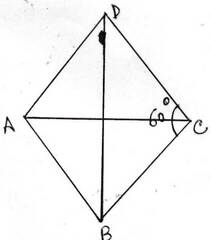
ABCD রম্বসের AB = 4 সেমি.।
∴ AB =BC =CD =DA =4 সেমি.
∆BCD ত্রিভুজের ক্ষেত্রে ,
∠BCD =60°
এবং BC = CD
∴ ∠CBD = ∠CDB =60°
∴ ∆CBD একটি সমবাহু ত্রিভুজ ।
∴ BC = CD = BD = 4সেমি.
WBBSE Class 9 Math Koshe Dekhi 6|সামান্তরিকের ধর্ম কষে দেখি 6
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
This website is best.To subject math
Thanks for the anushilan website.
Thanks for the solutions ✌🏻