Ganit Prabha Class 8 Koshe Dekhi 8|সমান্তরাল সরলরেখা ও ছেদকের ধর্ম কষে দেখি ৮|গণিতপ্রভা অষ্টম শ্রেণি (ক্লাস ৮ ) সমাধান|WBBSE Class 8 Math Solution Of Chapter 8
গণিতপ্রভা অষ্টম শ্রেণির বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।
Ganit Prabha Class 8 Koshe Dekhi 8|সমান্তরাল সরলরেখা ও ছেদকের ধর্ম কষে দেখি ৮|গণিতপ্রভা অষ্টম শ্রেণি (ক্লাস ৮ ) সমাধান|WBBSE Class 8 Math Solution Of Chapter 8
Koshe Dekhi 8
1. চন্দ্রা লাইন টানা খাতার পাতা নিল । দুটি লাইনের মাঝে একটি ছেদক টানল । এর ফলে 4 জোড়া অনুরূপ কোণ, 2 জোড়া একান্তর কোণ ও 2 জোড়া একই পাশের অন্তঃস্থ কোণ তৈরি হলো । তাদের খুঁজে দিই ও লিখি । চাঁদার সাহায্যে মেপে যাচাই করি যে (i) অনুরূপ কোণগুলি পরস্পর সমান, (ii) একান্তর কোণগুলি পরস্পর সমান ও (iii) একই পাশের অন্তঃস্থ কোণগুলি পরস্পর সম্পূরক ।
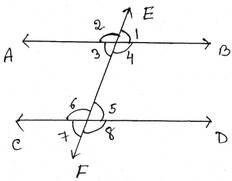
সমাধানঃ ধরি, AB ও CD হল দুটি লাইন । ছেদকটি হল EF , AB ও CD সরলরেখা দুটিকে EF ছেদ করার ফলে ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7, ∠8 কোণগুলি উৎপন্ন হল ।
∴ অনুরূপ কোণগুলি হল, (∠1, ∠5), (∠2, ∠6), (∠3, ∠7), ও (∠4, ∠8)
একান্তর কোণগুলি হল (∠3, ∠5), (∠4, ∠6)
এবং একই দিকের অন্তঃস্থ কোণ (∠4, ∠5), (∠3, ∠6)
চাঁদার সাহায্যে মেপে পেলাম,
∠1=450 , ∠2=1350 , ∠3=450 , ∠4=1350 , ∠5=450 , ∠6=1350 ,
চাঁদার সাহায্যে মেপে পেলাম ,
(i) অনুরূপ কোণগুলি হল –
∠1=∠5=450, ∠2=∠6=1350, ∠3=∠7=450, ∠4 =∠8=1350,
(ii) একান্তর কোণগুলি হল ∠1=∠5=450, ∠4=∠6=1350
(iii) একই পাশে অন্তঃস্থ কোণের সমষ্টি
∠4+∠5=1800 ∠3+∠6=1800
∴ একই পাশের অন্তঃস্থ কোণগুলির পরস্পর সম্পূরক ।
2. পাশের ছবির কোণগুলি দেখি ও কোনগুলি অনুরূপ কোণ, কোনগুলি একই পাশের অন্তঃস্থ কোণ লিখি ।
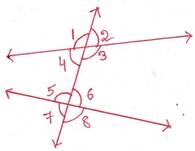
সমাধানঃ চিত্র থেকে পাই,
অনুরূপ কোণগুলি হল (∠1, ∠5), (∠2, ∠6), (∠3, ∠8), ও (∠4, ∠7)
একই পাশের অন্তঃস্থ কোণগুলি হল (∠3, ∠6), (∠4, ∠5)
3.AB||CD হলে নীচের কোণগুলির মান লিখি –
(a)
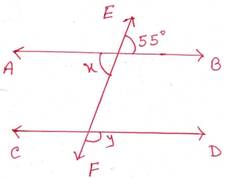
সমাধানঃ
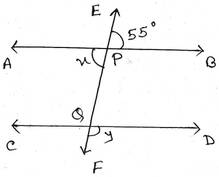
ধরি, EF ছেদক AB ও CD সরলরেখাকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে।
∴ ∠APQ=বিপ্রতীপ ∠BPE
∴ x=550
∠APQ এবং ∠CQP একই পাশের অন্থঃস্থ কোণ
∴ ∠APQ+∠CQP= 1800
∴ ∠CQP= 1800 -∠APQ = 1800–550 = 1250
আবার , ∠CQP = বিপ্রতীপ ∠DQF =y
সুতরাং, y= 1250
Ganit Prabha Class 8 Koshe Dekhi 8|সমান্তরাল সরলরেখা ও ছেদকের ধর্ম কষে দেখি ৮
(b)
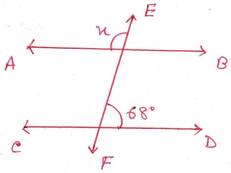
সমাধানঃ
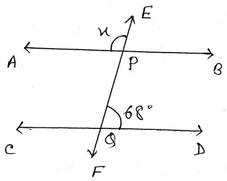
ধরি, EF ছেদক , AB ও CD সরলরেখাকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে।
∠BPQ ও ∠DQP একই পাশের অন্তঃস্থ কোণ
সুতরাং, ∠BPQ+∠DQP = 1800
∴ ∠BPQ =1800-∠DQP = 1800 -680 =1120
আবার , ∠APE = বিপ্রতীপ ∠BPQ
∠APE =1120
∴ x=1120
(c)
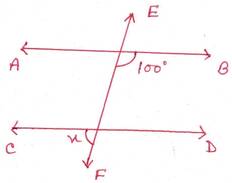
সমাধানঃ
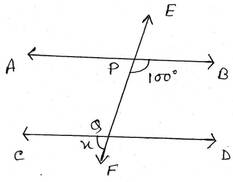
ধরি, EF ছেদক AB ও CD সরলরেখাকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে।
∠BPQ ও ∠DQP একই পাশের অন্তঃস্থ কোণ
সুতরাং, ∠BPQ+∠DQP = 1800
∴ ∠DQP = 1800-∠BPQ = 1800 -1000 =800
আবার, ∠CQF=বিপ্রতীপ ∠DQP
∴ x=800
4. পাশের ছবির XY||PQ হলে 7টি কোণের মান লিখি ।
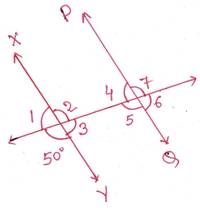
সমাধানঃ
∠1+500 = 1800
∴ ∠1=1800-500=1300
∠2 =500 [বিপ্রতীপ কোণ ]
∠3 =∠1=1300 [∵∠1, ∠3 পরস্পর বিপ্রতীপ কোণ ]
∠4 =∠1=1300 [∵∠1, ∠4 পরস্পর অনুরূপ কোণ ]
∠5 =∠2=500 [∵∠5, ∠2 পরস্পর একান্তর কোণ ]
∠6 =∠3=1300 [∵∠6, ∠3 পরস্পর অনুরূপ কোণ
∠7 =∠2=500 [∵∠7, ∠2 পরস্পর অনুরূপ কোণ ]
5. নীচের AB ও CD সরলরেখা দুটি সমান্তরাল কিনা কোণের মান দেখে যুক্তি দিয়ে লিখি –
(i)
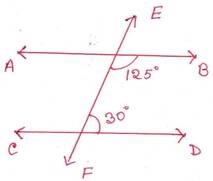
সমাধানঃ
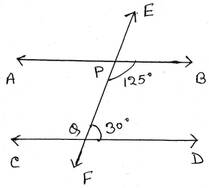
ধরি, EF ছেদক AB ও CD সরলরেখাকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে।
∠BPQ ও ∠DQP একই পাশের অন্তঃস্থ কোণ
∴ ∠BPQ + ∠DQP =1250+300=1550≠1800
∠BPQ ও ∠DQP একই পাশের অন্তঃস্থ কোণ দুটি পরস্পর সম্পূরক কোণ নয় ।
সুতরাং, AB ও CD সরলরেখা দুটি সমান্তরাল নয় ।
Ganit Prabha Class 8 Koshe Dekhi 8|সমান্তরাল সরলরেখা ও ছেদকের ধর্ম কষে দেখি ৮
5. নীচের AB ও CD সরলরেখা দুটি সমান্তরাল কিনা কোণের মান দেখে যুক্তি দিয়ে লিখি ।
(ii)
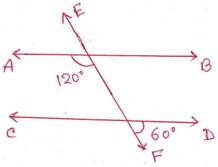
সমাধানঃ
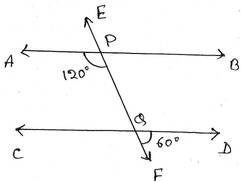
ধরি, EF ছেদক AB ও CD সরলরেখাকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে।
∠CQP = বিপ্রতীপ ∠DQF =600
∠APQ ও ∠CQP একই পাশের অন্তঃস্থ কোণ
∴ ∠APQ+∠CQP =1200 +600 = 1800
∴ ∠APQ ও ∠CQP একই পাশের অন্তঃস্থ কোণ দুটি পরস্পর সম্পূরক কোণ ।
সুতরাং, AB ও CD সরলরেখা দুটি সমান্তরাল ।
5. নীচের AB ও CD সরলরেখা দুটি সমান্তরাল কিনা কোণের মান দেখে যুক্তি দিয়ে লিখি ।
(iii)
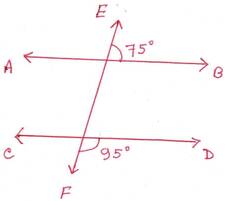
সমাধানঃ
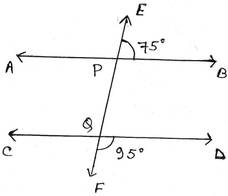
ধরি, EF ছেদক AB ও CD সরলরেখাকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে।
∠EPB +∠BPQ =1800
বা, ∠BPQ =1800 – ∠EPB
∴ ∠BPQ = 1800 -750 =1050
∠BPQ ও ∠DQF পরস্পর অনুরূপ কোণ
∠BPQ=1050 এবং ∠DQF =950
∴ ∠BPQ ≠ ∠DQF
সুতরাং, AB ও CD সরলরেখা দুটি সমান্তরাল নয় ।
গণিতপ্রভা অষ্টম শ্রেণির বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।
6. চিত্রে AB||CD এবং ∠EGB = 500; ∠AGE ,∠AGH, ∠BGH, ∠GHC, ∠GHD, ∠CHF এবং ∠DHF এর পরিমাপ লিখি ।
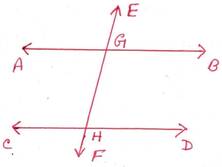
সমাধানঃ ∠EGB+∠AGE=1800
বা, ∠AGE=1800 – ∠EGB
∴ ∠AGE = 1800 -500 =1300
∠AGH = বিপ্রতীপ ∠EGB =500
∠BGH = বিপ্রতীপ ∠AGE =1300
∠GHC = অনুরূপ ∠AGE =1300
∠GHD = অনুরূপ ∠EGB =500
∠CHF = বিপ্রতীপ ∠GHD =500
∠DHF = বিপ্রতীপ ∠GHC =1300
Ganit Prabha Class 8 Koshe Dekhi 8|সমান্তরাল সরলরেখা ও ছেদকের ধর্ম কষে দেখি ৮
7. চিত্রে AB||CD; ∠PQR এর পরিমাপ লিখি ।
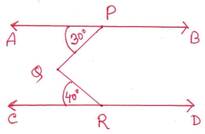
সমাধানঃ
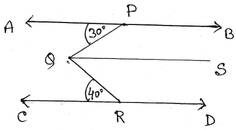
Q বিন্দু থেকে AB এর সমান্তরাল সরলরেখা QS অঙ্কন করলাম ।
∴ AB||QS||CD [∵AB||CD]
∠PQS = একান্তর ∠APQ =300
এবং ∠RQS= একান্তর ∠CRQ= 400
∠PQR=∠PQS+∠RQS =300 + 400 = 700
∴ ∠PQR = 700
8. চিত্রে PQ||RS, ∠BPQ = 400, ∠BPR = 1550,এবং ∠CRS = 700, ∆ APR এর কোণগুলির পরিমাপ লিখি ।
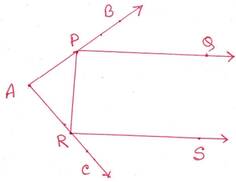
সমাধানঃ AB সরলরেখার উপর PR দণ্ডায়মান
সুতরাং, ∠APR+∠BPR=1800
∴ ∠APR =1800 – ∠BPR = 1800-1550 =250
আবার, ∠RPQ = ∠BPR-∠BPQ
∴ ∠RPQ =1550 – 400= 1150
∠RPQ এবং ∠PRS একই দিকের অন্তঃস্থ কোণ [∵ PQ||RS এবং PR ছেদক]
সুতরাং, ∠RPQ+∠PRS=1800 [∵ PQ||RS]
∴ ∠PRS =1800 -∠RPQ = 1800– 1150=650
এখন , ∠ARP+∠PRS+∠CRS=1800
বা, ∠ARP = 1800 -∠PRS – ∠CRS
বা, ∠ARP =1800 -650-700=450
∆APR এর ∠APR =250 এবং ∠ARP =450
∴ ∠PAR =1800 -250-450=1100
∆ APR এর ∠APR =250, ∠ARP =450 এবং ∠PAR =1100
Ganit Prabha Class 8 Koshe Dekhi 8|সমান্তরাল সরলরেখা ও ছেদকের ধর্ম কষে দেখি ৮
9. AB এবং CD দুটি সরলরেখার ভিতর O যেকোনো একটি বিন্দু । OP ও OQ যথাক্রমে AB CD সরলরেখার উপর লম্ব । প্রমাণ করি যে P,O,Q বিন্দু তিনটি সমরেখ ।
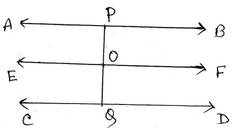
প্রদত্তঃ AB এবং CD দুটি সরলরেখার ভিতর O যেকোনো একটি বিন্দু এবং OP⊥ AB, OQ ⊥ CD
প্রমাণ্যঃ P,O,Q বিন্দু তিনটি সমরেখ।
অঙ্কনঃ O বিন্দু দিয়ে AB সরলরেখার সমান্তরাল সরলরেখা EF অঙ্কন করলাম ।
প্রমাণঃ AB||EF [অঙ্কনানুসারে]
∴ ∠BPO+ ∠POF=1800 [ ভেদকের একই দিকের অন্তঃস্থ কোণ]
আবার, ∠BPO=900
∴ ∠POF=1800 – 900=900
CD||EF [∵AB||EF এবং AB||CD]
∴ ∠DQO+ ∠QOF=1800 [ভেদকের একই দিকের অন্তঃস্থ কোণ]
আবার, ∠DQO=900
∴ ∠QOF=1800 – 900=900
∠POF ও ∠QOF হল পরস্পর সন্নিহিত কোণ এবং ∠POF+ ∠QOF=1800
∴ PO এবং QO একই সরলরেখায় অবস্থিত
অর্থাৎ, P,O,Q বিন্দু তিনটি সমরেখ [প্রমাণিত]
10. দুটি কোণের প্রতিজোড়া বাহু পরস্পর সমান্তরাল। প্রমান করি যে, কোণদুটি সমান অথবা পরস্পর সম্পূরক ।
চিত্র 1
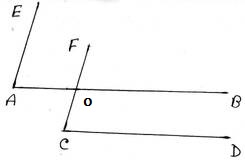
চিত্র 2
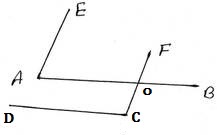
প্রদত্তঃ 1 নং চিত্রে , ∠EAB এর AE ও AB বাহু যথাক্রমে ∠FCD এর CF ও CD বাহুর সঙ্গে সমান্তরাল । 2 নং চিত্রে ,∠EAB এর AE ও AB বাহু যথাক্রমে ∠FCD এর CF ও DC বাহুর সঙ্গে সমান্তরাল । উভয় চিত্রে AB ও CF সরলরেখা দুটি O বিন্দুতে ছেদ করেছে ।
প্রামাণ্য: চিত্র 1 এর ক্ষেত্রে ∠EAB=∠FCD এবং চিত্র 2 এর ক্ষেত্রে ∠EAB+∠FCD =1800
প্রমাণঃ যেহেতু, AE || CF এবং AB ভেদক
∴ ∠EAB = অনুরূপ ∠FOB —-(i)
চিত্র 1 এর ক্ষেত্রে ,
AB || CD এবং CF ভেদক
∴ ∠FOB = অনুরূপ ∠FCD —-(ii)
(i) নং ও (ii) নং থেকে পাই,
∠EAB =∠FCD [প্রমাণিত]
চিত্র 2 এর ক্ষেত্রে,
AB || DC এবং CF ভেদক
∴ ∠FOA = অনুরূপ ∠FCD —(iii)
AE || CF এবং AB ভেদক
∴ ∠EAB+ ∠FOA =1800 [ভেদকের একই দিকের অন্তঃস্থ কোণ]
∴ ∠EAB+ ∠FCD =1800 [(iii)নং থেকে পাই] [প্রমাণিত]
Ganit Prabha Class 8 Koshe Dekhi 8|সমান্তরাল সরলরেখা ও ছেদকের ধর্ম কষে দেখি ৮
11. ABCD সামান্তরিকের AC কর্ণ ∠BAD কে সমদ্বিখণ্ডিত করে । প্রমাণ করি যে, AC কর্ণ ∠BCD কেও সমদ্বিখণ্ডিত করে ।
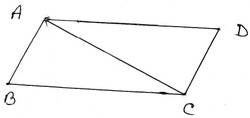
প্রদত্তঃ ABCD সামান্তরিকের AC কর্ণ ∠BAD কে সমদ্বিখণ্ডিত করে অর্থাৎ
∠BAC = ∠DAC
প্রামাণ্যঃ AC কর্ণ ∠BCD কে সমদ্বিখণ্ডিত করে অর্থাৎ ∠ACB= ∠ACD
প্রমাণঃ ∠BAC = ∠DAC [প্রদত্ত] —-(i)
সামান্তরিকের বিপরীত বাহু পরস্পর সমান্তরাল ।
সুতরাং, AD || BC এবং AB || DC
AD || BC এবং AC ছেদক
∴ ∠DAC = ∠ACB [একান্তর কোণ] —- (ii)
আবার, AB || DC এবং AC ছেদক
∴ ∠BAC = ∠ACD [একান্তর কোণ] —- (iii)
(i)ও (ii) থেকে পাই, ∠BAC = ∠ACB —- (iv)
(iii)ও (iv) থেকে পাই, ∠ACB = ∠ACD [ প্রমাণিত ]
∴ AC কর্ণ ∠BCD কে সমদ্বিখণ্ডিত করে ।
12. ABCD সামন্তরিকের একটি কোণ সমকোণ হলে, প্রতিটি কোণই সমকোণ ।
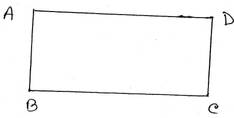
প্রদত্তঃ ধরি, ABCD সামন্তরিকের ∠B = 900
প্রামাণ্যঃ সামন্তরিকের বাকি তিনটি কোণ সমকোণ । অর্থাৎ, ∠A =∠C=∠D= 900
প্রমাণঃ সামান্তরিকের বিপরীত বাহু পরস্পর সমান্তরাল
সুতরাং, AD || BC এবং AB || DC
AD || BC এবং AB ছেদক
∴ ∠A+∠B = 1800 [ছেদকের একই দিকের অন্তঃস্থ কোণ]
∴ ∠A = 1800-∠B= 1800-900=900
AB || DC এবং BC ছেদক
∴ ∠B+∠C = 1800 [ ছেদকের একই দিকের অন্তঃস্থ কোণ]
∴ ∠C = 1800-∠B= 1800-900=900
AD || BC এবং DC ছেদক
∴ ∠C+∠D = 1800 [ ছেদকের একই দিকের অন্তঃস্থ কোণ]
∴ ∠D = 1800-∠C= 1800-900=900
সুতরাং, ∠A =∠C=∠D= 900 [প্রমাণিত ]
গণিতপ্রভা অষ্টম শ্রেণির বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।