WBBSE Class 9 Math Koshe Dekhi 19|স্থানাঙ্ক জ্যামিতি সরলরেখাংশের অন্তর্বিভক্ত ও বহির্বিভক্ত কষে দেখি ১৯|কষে দেখি 19 নবম শ্রেণি (ক্লাস ৯) সমাধান |গনিত প্রকাশ নবম শ্রেণি সমাধান|Gonit Prokash Class 9 Solution Of Chpater 19.
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।
গণিত প্রকাশ দশম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।
WBBSE Class 9 Math Koshe Dekhi 19|স্থানাঙ্ক জ্যামিতি সরলরেখাংশের অন্তর্বিভক্ত ও বহির্বিভক্ত কষে দেখি ১৯ |কষে দেখি 19 নবম শ্রেণি (ক্লাস ৯) সমাধান|গনিত প্রকাশ নবম শ্রেণি সমাধান|Ganit Prakash Class 9(IX) Solution Of Chpater 19.
Koshe Dekhi 19|কষে দেখি ১৯
1. নীচের বিন্দুদ্বয়ের সংযোজক সরলরেখাগুলি যে বিন্দুতে প্রদত্ত অনুপাতে বিভক্ত তার স্থানাঙ্ক নির্ণয় করি ।
(i) (6,-14) এবং (-8,10) ; 3: 4 অনুপাতে অন্তঃস্থভাবে ।
সমাধানঃ যে বিন্দু (6,-14) এবং (-8,10) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশকে 3 :4 অনুপাতে অন্তর্বিভক্ত করেছে তা হল –
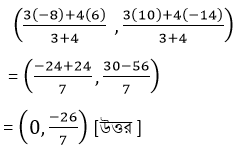
WBBSE Class 9 Math Koshe Dekhi 19|স্থানাঙ্ক জ্যামিতি সরলরেখাংশের অন্তর্বিভক্ত ও বহির্বিভক্ত কষে দেখি ১৯
(ii) (5,3) এবং (-7,-2) ; 2:3 অনুপাতে অন্তঃস্থভাবে
সমাধানঃ যে বিন্দু (5,3) এবং (-7,-2) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশকে 2:3 অনুপাতে অন্তর্বিভক্ত করেছে তা হল –
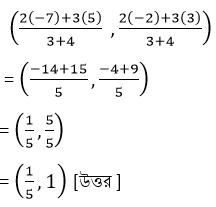
WBBSE Class 9 Math Koshe Dekhi 19|স্থানাঙ্ক জ্যামিতি সরলরেখাংশের অন্তর্বিভক্ত ও বহির্বিভক্ত কষে দেখি ১৯
(iii) (-1,2) এবং (4,-5) ; 3:2 অনুপাতে বহিঃস্থভাবে ।
সমাধানঃ যে বিন্দু (-1,2) এবং (4,-5) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশকে 3:2 অনুপাতে বহির্বিভক্ত করেছে তা হল –
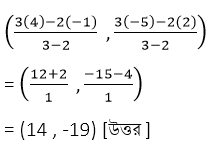
(iv) (3,2) এবং (6 ,5) ; 2:1 অনুপাতে বহিঃস্থভাবে ।
সমাধানঃ যে বিন্দু (3,2) এবং (6,5) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশকে 2:1 অনুপাতে বহির্বিভক্ত করেছে তা হল –
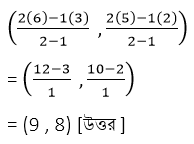
= (9,8) [উত্তর]
WBBSE Class 9 Math Koshe Dekhi 19|স্থানাঙ্ক জ্যামিতি সরলরেখাংশের অন্তর্বিভক্ত ও বহির্বিভক্ত কষে দেখি ১৯
2. নীচের প্রত্যেক বিন্দুগুলোর সংযোজক সরলরেখাংশগুলির মধ্যবিন্দুর স্থানাঙ্ক নির্ণয় করিঃ
(i) (5,4) এবং (3,-4)
সমাধানঃ (5,4) এবং (3,-4) বিন্দুদ্বয়ের সংযোজক সরল রেখাংশের মধ্যবিন্দুর স্থানাঙ্ক –
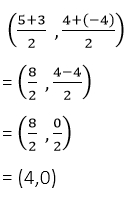
(ii) (6,0) এবং (0 ,7)
সমাধানঃ (6,0) এবং (0 ,7) বিন্দুদ্বয়ের সংযোজক সরল রেখাংশের মধ্যবিন্দুর স্থানাঙ্ক –
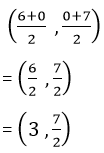
= (3, 7/2) [উত্তর ]
WBBSE Class 9 Math Koshe Dekhi 19|স্থানাঙ্ক জ্যামিতি সরলরেখাংশের অন্তর্বিভক্ত ও বহির্বিভক্ত কষে দেখি ১৯
3. (1,3) বিন্দুটি (4,6 ) ও (6,5) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশ কী অনুপাতে বিভক্ত হয়েছে হিসাব করে লিখি ।
সমাধানঃ ধরি , (1,3) বিন্দুটি (4,6 ) ও (6,5) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশ – কে m:n অনুপাতে বিভক্ত করে ।
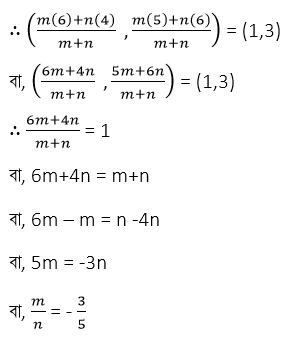
[ঋণাত্মক চিহ্ন – এর অর্থ বহির্বিভক্ত করা ]
∴ (1,3) বিন্দুটি , (4,6 ) ও (6,5) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশ –কে 3:5 অনুপাতে বহির্বিভক্ত করেছে ।
WBBSE Class 9 Math Koshe Dekhi 19|স্থানাঙ্ক জ্যামিতি সরলরেখাংশের অন্তর্বিভক্ত ও বহির্বিভক্ত কষে দেখি ১৯
4. (7,3) ও (-9,6) বিন্দুদ্বয়ের সংযোজক সরল রেখাংশ y –অক্ষ দ্বারা কী অনুপাতে বিভক্ত হয়েছে হিসাব করে লিখি ।
সমাধানঃ ধরি , (7,3) ও (-9,6) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশ y –অক্ষ দ্বারা m : n অনুপাতে বিভক্ত হয়েছ ।
∴ y – অক্ষ এবং (7,3) ও (-9,6) বিন্দুদ্বয়ের সংযোজক সরল রেখাংশের ছেদ বিন্দুর স্থানাঙ্ক –
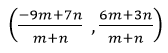
যেহেতু , y অক্ষের ওপর কোনো বিন্দুর ভুজ শূন্য হয়

∴ (7,3) ও (-9,6) বিন্দুদ্বয়ের সংযোজক সরল রেখাংশ y –অক্ষ দ্বারা 7:9 অনুপাতে অন্তর্বিভক্ত হয়েছে ।
WBBSE Class 9 Math Koshe Dekhi 19|স্থানাঙ্ক জ্যামিতি সরলরেখাংশের অন্তর্বিভক্ত ও বহির্বিভক্ত কষে দেখি ১৯
5. প্রমাণ করি যে, A (7,3) , B(9,6) , C (10,12) এবং D (8 ,9) বিন্দুগুলি পরপর যুক্ত করলে সামান্তরিক গঠিত হবে।

∴ ABCD একটি সামান্তরিক ।
WBBSE Class 9 Math Koshe Dekhi 19|স্থানাঙ্ক জ্যামিতি সরলরেখাংশের অন্তর্বিভক্ত ও বহির্বিভক্ত কষে দেখি ১৯
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।
6. যদি , (3,2) ,(6,3) ,(x,y) এবং (6,5) বিন্দুগুলি পরস্পর যুক্ত করলে একটি সামান্তরিক গঠিত হয় , তাহলে (x,y) কত হবে হিসাব করে লিখি ।
সমাধানঃ ধরি , ABCD একটি সামান্তরিক যার A, B ,C এবং D বিন্দুর স্থানাঙ্ক যথাক্রমে (3,2) ,(6,3) ,(x,y) এবং (6,5) ।

যেহেতু সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে ,
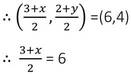
বা,3 +x = 12
বা, x = 12- 3
বা, x = 9
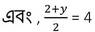
বা , 2 +y = 8
বা, y = 8-2
বা , y = 6
∴ (x,y) = (9,6) [উত্তর ]
WBBSE Class 9 Math Koshe Dekhi 19|স্থানাঙ্ক জ্যামিতি সরলরেখাংশের অন্তর্বিভক্ত ও বহির্বিভক্ত কষে দেখি ১৯
7. যদি , (x1,y1),(x2,y2) , (x3,y3) এবং (x4,y4) বিন্দুগুলি পরস্পর যুক্ত করলে একটি সামান্তরিক গঠিত হয় ,তাহলে প্রমাণ করি যে , x1+x3 = x2+x4 এবং y1+y3 = y2+y4
সমাধানঃ ধরা যাক , ABCD একটি সামান্তরিক যার A,B,C এবং D বিন্দুর স্থানাঙ্ক যথাক্রমে (x1,y1),(x2,y2) , (x3,y3) এবং (x4,y4) ।

8. ABC ত্রিভুজের A ,B ও C শীর্ষবিন্দুর স্থানাঙ্ক যথাক্রমে (-1,3) ,(1,-1) এবং (5,1) ; AD মধ্যমার দৈর্ঘ্য হিসাব করে লিখি ।
সমাধানঃ যেহেতু , AD মধ্যমা ,
∴ D , BC –এর মধ্যবিন্দু
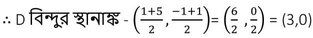

WBBSE Class 9 Math Koshe Dekhi 19|স্থানাঙ্ক জ্যামিতি সরলরেখাংশের অন্তর্বিভক্ত ও বহির্বিভক্ত কষে দেখি ১৯
9. একটি ত্রিভুজের তিনটি শীর্ষবিন্দুর স্থানাঙ্ক (2, -4) ,(6 ,-2) এবং (-4,2) ; ত্রিভুজটির তিনটি মধ্যমার দৈর্ঘ্য নির্ণয় করি ।
সমাধানঃ ধরা যাক, ABC ত্রিভুজের A ,B এবং C বিন্দুর স্থানাঙ্ক যথাক্রমে (2, -4) ,(6 ,-2) এবং (-4,2)এবং AB ,BC এবং CA বাহুগুলির মধ্যবিন্দু যথাক্রমে D ,E এবং F ।
∴ D বিন্দুর স্থানাঙ্ক –



∴ ABC ত্রিভুজের মধ্যমা তিনটির দৈর্ঘ্য যথাক্রমে √17 একক , 5√2 একক এবং √89 একক ।
WBBSE Class 9 Math Koshe Dekhi 19|স্থানাঙ্ক জ্যামিতি সরলরেখাংশের অন্তর্বিভক্ত ও বহির্বিভক্ত কষে দেখি ১৯
10. একটি ত্রিভুজের বাহুগুলির মধ্যবিন্দুর স্থানাঙ্ক (4,3) ,(-2,7) এবং (0,11) ; ত্রিভুজটির শীর্ষবিন্দু তিনটির স্থানাঙ্ক নির্ণয় করি ।
সমাধানঃ ধরা যাক , ABC ত্রিভুজের A ,B এবং C শীর্ষবিন্দুগুলির স্থানাঙ্ক যথাক্রমে (x1,y1) ,(x2,y2 ) এবং (x3,y3) ।
ABC ত্রিভুজের AB বাহুর মধ্যবিন্দু (4,3)
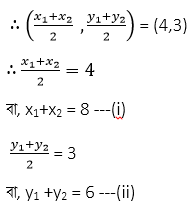
ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু (-2,7)
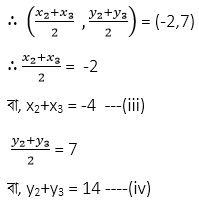
আবার ,ABC ত্রিভুজের CA বাহুর মধ্যবিন্দু (0,11)
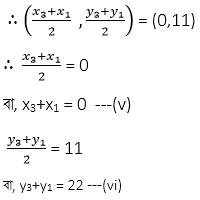
এখন , (i) ,(iii) এবং (v) নং সমীকরণ যোগ করে পাই ,
x1+x2 +x2+x3+x3+x1 = 8-4
বা, 2(x1+x2+x3) = 4
বা, x1+x2+x3 = 4/2
বা, x1+x2+x3= 2 — (vii)
(ii) , (iv) এবং (vi) নং সমীকরণ যোগ করে পাই ,
y1+y2 +y2+y3+y3+y1 = 6+14+22
বা, 2 (y1+y2+y3) = 42
বা, y1+y2+y3 = 21 —-(viii)
(vii) নং সমীকরণ থেকে (iii) নং সমীকরণ বিয়োগ করে পাই ,
x1+x2+x3 – x2-x3 = 2-(-4)
বা, x1 = 6
আবার , (viii) নং সমীকরণ থেকে (iv) নং সমীকরণ বিয়োগ করে পাই ,
y1+y2+y3 –y2 –y3 = 21- 14
বা, y1 = 7
∴ A-বিন্দুর স্থানাঙ্ক (6,7)
(vii) নং সমীকরণ থেকে (v) নং সমীকরণ বিয়োগ করে পাই ,
x1+x2+x3 – x3– x1 = 2 -0
বা, x2 = 2
(viii) নং সমীকরণ থেকে (vi) নং সমীকরণ বিয়োগ করে পাই ,
y1+y2+y3 – y3-y1 = 21 -22
বা, y2 = -1
∴ B বিন্দুর স্থানাঙ্ক (2,-1) ।
(vii) নং সমীকরণ থেকে (i) নং সমীকরণ বিয়োগ করে পাই ,
x1+x2+x3 – x1-x2 = 2-8
বা, x3 = -6
(viii) নং সমীকরণ থেকে (ii) নং সমীকরণ বিয়োগ করে পাই ,
y1+y2+y3 – y1– y2 = 21- 6
বা, y3 = 15
∴C বিন্দুর স্থানাঙ্ক (-6,15) ।
∴ ত্রিভুজটির তিনটি শীর্ষবিন্দু যথাক্রমে (6,7) , (2,-1) এবং (-6,15) ।
WBBSE Class 9 Math Koshe Dekhi 19|স্থানাঙ্ক জ্যামিতি সরলরেখাংশের অন্তর্বিভক্ত ও বহির্বিভক্ত কষে দেখি ১৯
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।
11. বহু বিকল্পীয় প্রশ্ন (M.C.Q):
(i) (l,2m) এবং (-l+2m ,2l-2m) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশের মধ্যবিন্দুর স্থানাঙ্ক
(a) (l,m)
(b) (l,-m)
(c ) (m,-l)
(d) (m,l)
Ans: (d) (m,l)
সমাধানঃ (l,2m) এবং (-l+2m ,2l-2m) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশের মধ্যবিন্দুর স্থানাঙ্ক –
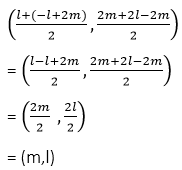
WBBSE Class 9 Math Koshe Dekhi 19|স্থানাঙ্ক জ্যামিতি সরলরেখাংশের অন্তর্বিভক্ত ও বহির্বিভক্ত কষে দেখি ১৯
(ii) A(1,5) এবং B (-4,7) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশকে P বিন্দু অন্তঃস্থ ভাবে 2:3 অনুপাতে বিভক্ত করলে P বিন্দুর ভুজ
(a) -1
(b) 11
(c ) 1
(d) -11
Ans: (a) -1
সমাধানঃ A(1,5) এবং B (-4,7) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশকে P বিন্দু অন্তঃস্থ ভাবে 2:3 অনুপাতে বিভক্ত করলে P বিন্দুর স্থানাঙ্ক –
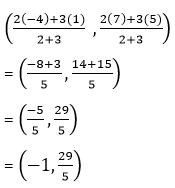
WBBSE Class 9 Math Koshe Dekhi 19|স্থানাঙ্ক জ্যামিতি সরলরেখাংশের অন্তর্বিভক্ত ও বহির্বিভক্ত কষে দেখি ১৯
(iii) একটি বৃত্তের ব্যাসের প্রান্তবিন্দুর স্থানাঙ্ক (7,9) এবং (-1,-3) ; বৃত্তের কেন্দ্রের স্থানাঙ্ক
(a) (3,3)
(b) (4,6)
(C ) (3,-3)
(d) (4,-6)
Ans: (a) (3,3)
সমাধানঃ আমারা জানি , ব্যাসের মধ্যবিন্দুই হল বৃত্তের কেন্দ্র ।
∴ কেন্দ্রের স্থানাঙ্ক –
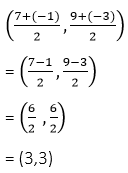
(iv) (2,-5) এবং (-3,-2) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশকে একটি বিন্দু 4:3 অনুপাতে বহিঃস্থ ভাবে বিভক্ত করেছে । ওই বিন্দুর কোটি
(a) -18
(b) -7
(c ) 18
(d) 7
Ans: (d) 7
সমাধানঃ (2,-5) এবং (-3,-2) বিন্দুদ্বয়ের সংযোজক সরলরেখাংশকে একটি বিন্দু 4:3 অনুপাতে বহিঃস্থ ভাবে বিভক্ত করেছে । ওই বিন্দুর স্থানাঙ্ক –
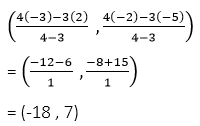
(v) PQRS সামান্তরিকের P(1,2) ,Q(4,6) ,R (5,7) এবং S(x,y) শীর্ষবিন্দু হলে ,
(a ) x =2 , y =4
(b) x =3 ,y =4
(c ) x=2 , y=3
(d) x =2 ,y =5
Ans: (c ) x=2 , y=3
সমাধানঃ PR কর্ণের মধ্যবিন্দুর স্থানাঙ্ক –

বা, 4+x = 6
বা, x = 6-4
বা, x =2
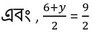
বা, 6 +y = 9
বা, y = 9-6
বা, y = 3
∴ x= 2 ,y = 3
WBBSE Class 9 Math Koshe Dekhi 19|স্থানাঙ্ক জ্যামিতি সরলরেখাংশের অন্তর্বিভক্ত ও বহির্বিভক্ত কষে দেখি ১৯
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।
12. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ
(i) একটি বৃত্তের কেন্দ্র C এবং ব্যাস AB ; A এবং C বিন্দুর স্থানাঙ্ক যথাক্রমে (6,-7) এবং (5,-2) হলে , B বিন্দুর স্থানাঙ্ক হিসাব করে লিখি ।
সমাধানঃ ধরি , B বিন্দুর স্থানাঙ্ক (x,y )
∴ (6+x/2 , -7+y/2) = (5,-2)
∴ 6+x/2 = 5
বা , 6+x = 10
বা, x = 4
এবং , -7+y/2 = -2
বা, -7+y = -4
বা, y = -4+7
বা, y = 3
∴ B বিন্দুর স্থানাঙ্ক (4,3) ।
(ii) P ও Q যথাক্রমে প্রথম ও তৃতীয় পাদে অবস্থিত এবং x অক্ষ ও y অক্ষ থেকে বিন্দুটির প্রত্যেকটির দূরত্ব যথাক্রমে 6 একক এবং 4 একক । PQ সরলরেখাংশের মধ্যবিন্দুর স্থানাঙ্ক লিখি ।
সমাধানঃ P ও Q যথাক্রমে প্রথম ও তৃতীয় পাদে অবস্থিত এবং x অক্ষ ও y অক্ষ থেকে বিন্দুটির প্রত্যেকটির দূরত্ব যথাক্রমে 6 একক এবং 4 একক ।
∴ P বিন্দুর স্থানাঙ্ক (4 , 6) এবং Q বিন্দুর স্থানাঙ্ক (-4 ,-6) ।
∴ PQ সরলরেখাংশের মধ্যবিন্দুর স্থানাঙ্ক –
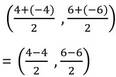
= (0,0)
(iii) A ও B বিন্দু যথাক্রমে দ্বিতীয় ও চতুর্থ পাদে অবস্থিত এবং x অক্ষ ও y অক্ষ থেকে বিন্দুদ্বয়ের প্রত্যেকটির দূরত্ব যথাক্রমে 8 একক ও 6 একক । AB সরলরেখাংশের মধ্যবিন্দুর স্থানাঙ্ক লিখি ।
সমাধানঃ A ও B বিন্দু যথাক্রমে দ্বিতীয় ও চতুর্থ পাদে অবস্থিত এবং x অক্ষ ও y অক্ষ থেকে বিন্দুদ্বয়ের প্রত্যেকটির দূরত্ব যথাক্রমে 8 একক ও 6 একক ।
∴ A বিন্দুর স্থানাঙ্ক – (-6 ,8) এবং B বিন্দুর স্থানাঙ্ক ( 6,-8)
∴ AB সরলরেখার মধ্যবিন্দুর স্থানাঙ্ক –
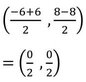
= (0,0)
∴ AB সরল রেখাংশের মধ্যবিন্দুর স্থানাঙ্ক (0,0) ।
(iv) AB সরলরেখার ওপর P একটি বিন্দু এবং AP =PB ; A ও B বিন্দুর স্থানাঙ্ক যথাক্রমে (3,-4) এবং (-5,2) ; P বিন্দুর স্থানাঙ্ক লিখি ।
সমাধানঃ AB সরলরেখার ওপর P একটি বিন্দু এবং AP =PB । ∴ P , AB –এর মধ্যবিন্দু ।
∴ P বিন্দুর স্থানাঙ্ক –

(v ) ABCD আয়তক্ষেত্রের বাহুগুলি অক্ষদ্বয়ের সমান্তরাল । B এবং D বিন্দুর স্থানাঙ্ক যথাক্রমে (7,3) এবং (2,6) ; A ও C বিন্দুদ্বয়ের স্থানাঙ্ক এবং AC কর্ণের মধ্যবিন্দুর স্থানাঙ্ক লিখি ।
সমাধানঃ ABCD আয়তক্ষেত্রের বাহুগুলি অক্ষদ্বয়ের সমান্তরাল । B এবং D বিন্দুর স্থানাঙ্ক যথাক্রমে (7,3) এবং (2,6) ।
∴ A বিন্দুর স্থানাঙ্ক – (2,3) এবং C বিন্দুর স্থানাঙ্ক (7,6) । [উত্তর]
AC –কর্ণের মধ্যবিন্দুর স্থানাঙ্ক –
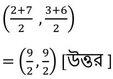
WBBSE Class 9 Math Koshe Dekhi 19|স্থানাঙ্ক জ্যামিতি সরলরেখাংশের অন্তর্বিভক্ত ও বহির্বিভক্ত কষে দেখি ১৯
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।
ধন্যবাদ। এই POST টি ভালো লাগলে SHARE করার অনুরোধ রইল । এইরকম আরও সুন্দর সুন্দর POST পেতে , আমাদের FACEBOOK PAGE টি LIKE করুন।
It’s an awesome website for WBBSE all subjects. I didn’t need any reference book as I have this website. It helped me a lot.
Thank you