Dighat Somikoron Koshe Dekhi 1.2 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.২

Dighat Somikoron Koshe Dekhi 1.2 Class 10| দ্বিঘাত সমীকরণ কষে দেখি ১.২|গণিত প্রকাশ সমাধান ক্লাস ১০(টেন) কষে দেখি 1.2|WBBSE Madhyamik Class 10(Ten) (X)Math Solution Of Chapter 1 Exercise 1.2 Quadratic Equation|Ganit Prakash somadhan Class 10.

Dighat Somikoron Koshe Dekhi 1.2 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.২|কষে দেখি 1.2 ক্লাস 10

1.নিচের প্রতি ক্ষেত্রে প্রদত্ত মান গুলি দ্বিঘাত সমীকরণের বীজ হবে কিনা যাচাই করে লিখি ঃ

(i) x²+x+1=0 , 1 ও -1

(ii) 8x²+7x=0 , 0 ও -2

(iii) x+$\frac{1}{\boldsymbol x}$=$\frac{13}{6}$, $\frac{5}{6}$ ও $\frac{4}{3}$

(iv) x²-√3x-6=0, -√3 ও 2√3

সমাধানঃ

(i) 1 এবং -1 প্রদত্ত সমীকরণটির বীজ হলে সমীকরণটিকে সিদ্ধ করবে ।

এখন, x²+x+1=0 সমীকরণে x স্থানে 1 এবং -1 বসিয়ে পাই ,

(1)²+1+1 = 1+1+1=3 ≠ 0

আবার, (-1)²+(-1)+1 =1-1+1=1≠ 0

সমীকরণটি 1 এবং -1 কোনোটিই দ্বারা সিদ্ধ নয় সুতরাং 1 এবং -1 প্রদত্ত দ্বিঘাত সমীকরণের বীজ হবে না।

(ii) 0 এবং 2 প্রদত্ত সমীকরণ টির বীজ হলে সমীকরণ টিকে সিদ্ধ করবে ।

এখন, 8x²+7x=0 সমীকরণটিতে x স্থানে 0 এবং 2 বসিয়ে পাই ,

8(0)²+7(0)=0

∴ 0, প্রদত্ত দ্বিঘাত সমীকরণটিকে সিদ্ধ করছে সুতরাং 0 প্রদত্ত দ্বিঘাত সমীকরণের একটি বীজ ।

আবার, 8(2)²+7(2) =32+14=46≠ 0

2 প্রদত্ত দ্বিঘাত সমীকরণটিকে সিদ্ধ করছে না সুতরাং 2 প্রদত্ত দ্বিঘাত সমীকরণের একটি বীজ নয় ।

(iii) $\frac{5}{6}$ এবং $\frac{4}{3}$ , প্রদত্ত দ্বিঘাত সমীকরণটির বীজ হলে সমীকরণটিকে সিদ্ধ করবে ।

এখন, x+$\frac{1}{x}$=$\frac{13}{6}$ সমীকরণটিতে x স্থানে $\frac{5}{6}$ এবং $\frac{4}{3}$ বসিয়ে পাই ,

$\frac{5}{6} + \frac{1}{\frac{5}{6}}$

= $\frac{5}{6} + \frac{6}{5}$

= $\frac{25 + 36}{30}$

= $\frac{61}{30} \neq \frac{13}{6}$

$\frac{4}{3} + \frac{1}{\frac{4}{3}}$

=$ \frac{4}{3} + \frac{3}{4}$

=$\frac{16 + 9}{12}$

= $\frac{25}{12} \neq \frac{13}{6}$

∴ $\frac{5}{6}$ এবং $\frac{4}{3}$ কোনোটিই প্রদত্ত দ্বিঘাত সমীকরণটির বীজ নয়।

(iv) -√3 এবং 2√3 প্রদত্ত সমীকরণ টির বীজ হলে সমীকরণ টিকে সিদ্ধ করবে ।

এখন, x²-√3x-6=0 সমীকরণটিতে x স্থানে √3 এবং 2√3 বসিয়ে পাই ,

(-√3)²-√3(-√3)-6=3+3-6=6-6=0

∴-√3 প্রদত্ত দ্বিঘাত সমীকরণটিকে সিদ্ধ করছে সুতরাং -√3 প্রদত্ত দ্বিঘাত সমীকরণের একটি বীজ হবে ।

আবার, (2√3)²-√3(2√3)-6=12-6-6=12-12=0

∴2√3 প্রদত্ত দ্বিঘাত সমীকরণটিকে সিদ্ধ করছে সুতরাং 2√3 প্রদত্ত দ্বিঘাত সমীকরণের একটি বীজ হবে ।

2(i) K এর কোন মানের জন্য 7x²+kx-3=0 দ্বিঘাত সমীকরণের একটি বীজ 2/3 হবে ?

সমাধানঃ

7×2+kx-3=0 দ্বিঘাত সমীকরণের একটি বীজ $\frac{2}{3}$ হলে , অবশ্যই $\frac{2}{3}$ সমীকরণটিকে সিদ্ধ করবে ।

$\therefore 7\left(\frac{2}{3}\right)^2 + {\mathrm{k}}\left(\frac{2}{3}\right) – 3 = 0$

$\Rightarrow 7\left(\frac{4}{9}\right) + \frac{2{\mathrm{k}}}{3} – 3 = 0$

$\Rightarrow \frac{28}{9} + \frac{2{\mathrm{k}}}{3} – 3 = 0$

$\Rightarrow \frac{28 + 6{\mathrm{k}} – 27}{9} = 0$

$\Rightarrow 6{\mathrm{k}} + 1 = 0$

$\Rightarrow 6{\mathrm{k}} = – 1$

$\Rightarrow {\mathrm{k}} = – \frac{1}{6}$

∴ K এর মান $- \frac{1}{6}$ হলে 7x²+kx-3=0 দ্বিঘাত সমীকরণের একটি বীজ $\frac{2}{3}$ হবে ।

2(ii)K এর কোন মানের জন্য  x² +3ax+k=0  দ্বিঘাত সমীকরণের একটি বীজ হবে –a ?

সমাধানঃ

x² +3ax+k=0 দ্বিঘাত সমীকরণের একটি বীজ –a

∴ -a সমীকরণ টিকে সিদ্ধ করবে  

X এরস্থানে –a বসিয়ে পাই ,

(-a)²+3a(-a)+k=0

বা, a²-3a²+k=0

বা,-2a²+k=0

বা, k=2a²

∴ k এর মান 2a² হলে দ্বিঘাত সমীকরণটির একটি বীজ হবে -a ।

3. যদি ax²+7x+b=0 দ্বিঘাত সমীকরণের দুটি বীজ $\frac{2}{3}$ এবং  -3 হয় তবে a ও b এর মান নির্ণয় করি ।

সমাধান ঃ

যদি ax²+7x+b=0 দ্বিঘাত সমীকরণের দুটি বীজ $\frac{2}{3}$ এবং-3 হয় তাহলে $\frac{2}{3}$ এবং -3 উভয়ই প্রদত্ত দ্বিঘাত সমীকরণটিকে সিদ্ধ করবে ।

x এর স্থানে $\frac{2}{3}$ এবং -3 বসিয়ে পাই ,

${\mathrm{a}}\left(\frac{2}{3}\right)^2 + 7\left(\frac{2}{3}\right) + {\mathrm{b}} = 0$

বা, $\frac{4{\mathrm{a}}}{9} + \frac{14}{3} + {\mathrm{b}} = 0$

বা, $\frac{4{\mathrm{a}} + 42 + 9{\mathrm{b}}}{9} = 0$

বা, 4a + 9b +42 = 0

বা, 4a+9b = -42

এবং a(-3)² + 7(-3)+b=0

বা, 9a-21+b=0

বা, 9a+b=21—(ii)

(ii) নং সমীকরণ কে 9 দ্বারা গুন করে (i) নং সমীকরণ বিয়োগ করে পাই ,

(4a+9b)-(81a+9b)=-42-189

বা, -77a = -231

বা , a = $\frac{ – 231}{ – 77}$

বা , a = 3

a এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই

4(3)+9b=-42

বা, 12+9b = -42

বা, 9b= -42-12

বা, 9b = -54

বা, b= -$\frac{ 54}{9}$

বা, b = -6

∴ ax²+7x+b=0 দ্বিঘাত সমীকরণের দুটি বীজ $\frac{ 2}{ 3}$ এবং-3 হলে, a=3 এবং b= -6 হবে।

4.সমাধান করি:

(i) 3y² -20=160-2y²

3y² -20=160-2y²

বা , 3y²+2y²=160+20

বা, 5y² =180

বা, y² = 180/5

বা, y² =36

বা, y= ±√36

বা, y =± 6

∴ নির্ণেয় সমাধান y=6 এবং y=-6

(ii) (2x+1)² +(x+1)²=6x+47

(2x+1)² +(x+1)²=6x+47

বা, (2x)²+2(2x)1+(1)² + (x)²+2x+(1)²=6x+47

বা, 4x² +4x +1 + x²+2x+1=6x+47

বা, 5x²+6x+2 =6x+47

বা, 5x²+6x+2-6x-47=0

বা, 5x²-45 =0

বা ,5x²=45

বা , x²=45/9

বা, x²=9

বা, x=±√9

বা, x = ±3

∴নির্ণেয় সমাধান x=3  এবং x=-3

(iii) (x-7)(x-9)=195

(x-7)(x-9)=195

বা, x(x-9)-7(x-9)=195

বা, x²-9x-7x+63=195

বা, x²-16x+63-195=0

বা, x²-16x-132=0

বা, x²-(22-6)x-132=0

বা, x²-22x+6x-132=0

বা, x(x-22)+6(x-22)=0

বা, (x-22)(x+6)=0

দুটি রাশির গুনফল শূন্য

হয় (x-22)=0

∴ x=22

অথবা , (x+6)=0

∴ x=-6

∴ নির্ণেয় সমাধান x= 22   এবং  x= -6

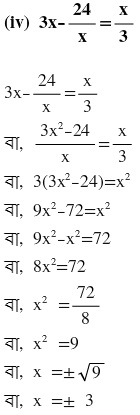
∴ নির্ণেয় সমাধান x=3 এবং x=-3

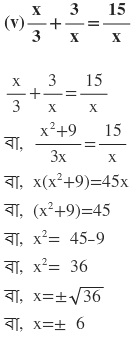
∴ নির্ণেয় সমাধান x=6 এবং x=-6

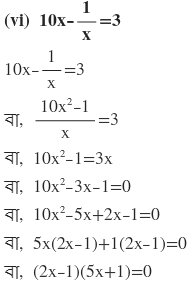
দুটি রাশির গুনফল শূন্য

হয় (2x-1)=0

2x=1

বা, x=1/2

অথবা (5x+1)=0

∴ 5x= -1

বা, x= -1/5

∴ নির্ণেয় সমাধান x=1/2 এবং x= -1/5

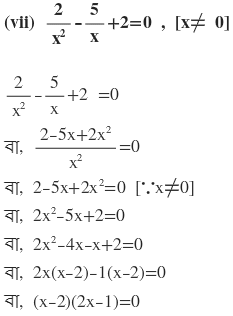
দুটি রাশির গুনফল শূন্য

হয় (x-2)=0

∴ x=2

অথবা (2x-1)=0

∴ 2x=1

বা, x= 1/2

∴ নির্ণেয় সমাধান x=2 এবং x=1/2 ।

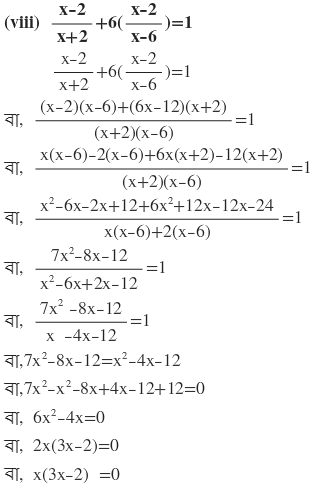
দুটি রাশির গুনফল শূন্য

হয় x=0

অথবা (3x-2)=0

বা, 3x=2

বা, x=2/3

∴ নির্ণেয় সমাধান x=0 এবং x=2/3

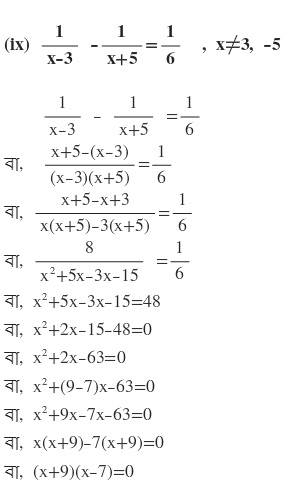
দুটি রাশির গুনফল শূন্য

হয় (x+9)=0

∴ x= -9

অথবা (x-7)=0

∴ x=7

∴ নির্ণেয় সমাধান x=-9 এবং x=7

আরও দেখুনঃ মাধ্যমিকের সকল বিষয়ের মক টেস্ট

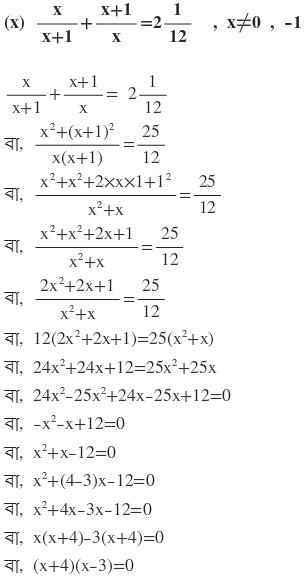
দুটি রাশির গুনফল শূন্য

হয় (x+4)=0

বা, x=-4

অথবা (x-3)=0

বা, x=3

∴ নির্ণেয় সমাধান x=3 এবং x=-4

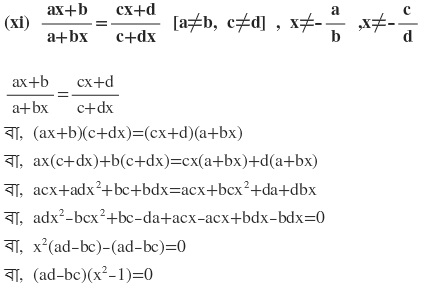
এখন দুটি রাশির গুনফল শূন্য

কিন্তু (ad-bc)≠ 0 কারণ a≠b এবং c≠d

   ∴ (x² -1)=0

বা ,   x² =1

বা,   x = ±√1

∴ নির্ণেয় সমাধান X= 1 এবং X= -1

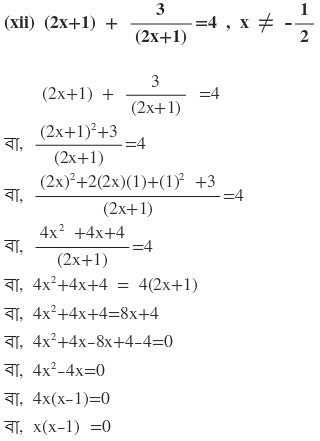
দুটি রাশির গুনফল শূন্য

হয় x=0

অথবা (x-1)=0

বা, x=1

∴ নির্ণেয় সমাধান x=0 এবং x= 1

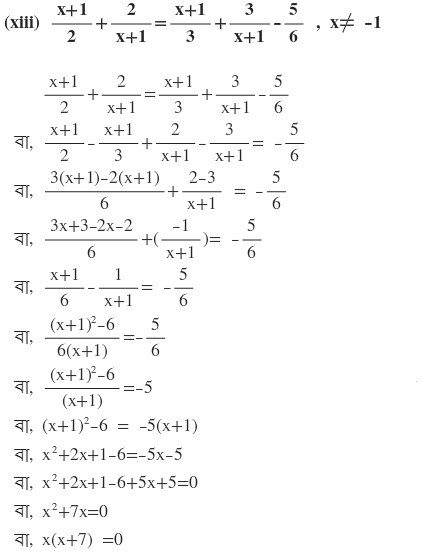
দুটি রাশির গুনফল শূন্য

হয় x=0

অথবা (x+7)=0

বা, x= -7

∴ নির্ণেয় সমাধান x= 0 এবং x=-7 ।

দুটি রাশির গুনফল শূন্য

হয়, (9x+68)=0

বা, 9x=-68

বা, x=-68/9

অথবা, (x-3)=0

বা, x=3

∴ নির্ণেয় সমাধান x=3 এবং x= -68/9

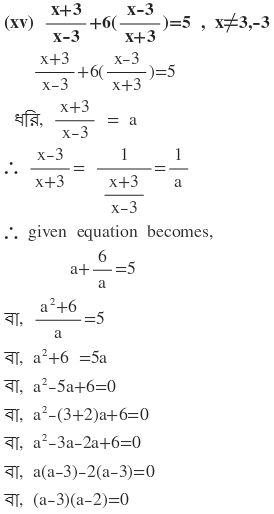
দুটি রাশির গুনফল শূন্য

হয় (a-3)=0

বা, a=3

অথবা, (a-2)=0

বা, a=2

∴ নির্ণেয় সমাধান x=6 এবং x= 9 ।

দুটি রাশির গুনফল শূন্য

হয়, (x+a)=0

বা, x= -a

অথবা, (x+b)=0

বা, x= -b

∴ নির্ণেয় সমাধান x=-a এবং x=-b

আরও দেখুনঃ মাধ্যমিকের সকল বিষয়ের মক টেস্ট

দুটি রাশির গুনফল শূন্য

হয় (m-3)=0

বা, m=3

অথবা (m-2)=0

বা, m=2

দুটি রাশির গুনফল শূন্য

হয় (x-a)=0

বা, x=a

অথবা (x+a+b)=0

বা, x=-(a+b)

∴ নির্ণেয় সমাধান x=a এবং x=-(a+b)

দুটি রাশির গুনফল শূন্য

হয় (x-7)=0

বা, x=7

অথবা (x+2)=0

বা, x=-2

∴ নির্ণেয় সমাধান x= 7 এবং x=-2

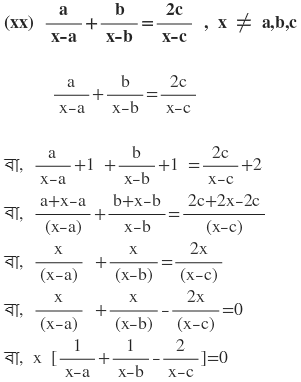
দুটি রাশির গুনফল শূন্য

হয় x=0

অথবা

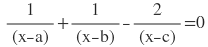
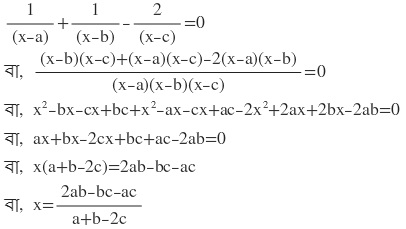
∴ নির্ণেয় সমাধান x=0 এবং x=(2ab-bc-ac)/(a+b-2c)

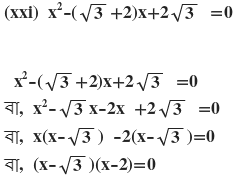
দুটি রাশির গুনফল শূন্য

হয়

∴ নির্ণেয় সমাধান

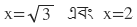
আরও দেখুনঃ মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধান

আরও দেখুনঃ গণিত প্রকাশ বই-এর সব অধ্যায়ের সমাধান

আরও দেখুনঃ মাধ্যমিকের সকল বিষয়ের মক টেস্ট

আরও দেখুনঃ WBBSE Official Site

ধন্যবাদ । এই POST টি ভাল লাগলে SHARE করার অনুরোধ রইল । এইরকম আরও সুন্দর সুন্দর POST পাওয়ার জন্য আমাদের FACEBOOK PAGE টি LIKE করুন ।প্রতিদিন মক টেস্টে অংশগ্রহণ করতে আমাদের টেলিগ্রাম গ্রুপে যুক্ত হোন ।