SN Dey Math Solution Of Class 12 Chapter 1 Relation

SN Dey Math Solution Of Class 12 Chapter 1 Relation|সৌরেন্দ্রনাথ দে গণিত সমাধান ক্লাস ১২ সম্মন্ধ | উচ্চমাধ্যমিক গণিত সমাধান ক্লাস ১২ সম্মন্ধ| WBCHSE Math Class 12 Chapter 1 Relation.

SN Dey Math Solution Of Class 12 Chapter 1 Relation|সৌরেন্দ্রনাথ দে গণিত সমাধান ক্লাস ১২ সম্মন্ধ | উচ্চমাধ্যমিক গণিত সমাধান ক্লাস ১২ সম্মন্ধ| WBCHSE Math Class 12 Chapter 1 Relation.

অতিসংক্ষিপ্ত প্রশ্নাবলীঃ

1.মনে করো A={1,3,5}, B={2,4,6) এবং R সম্বন্ধ নিম্নরূপে সঙ্গাত

xRy ⇒ (x+y) এর মান জোড় , দেখাও যে A থেকে B তে R একটি শূন্য সম্বন্ধে প্রকাশ করে

সমাধান ঃ A সেটের পদ্গুলি বিজোড় এবং B সেটের পদ্গুলি জোড় । যেহেতু , একটি বিজোড় ও একটি জোড় সংখ্যার যোগফল সর্বদা বিজোড় সংখ্যা হয় সুতরাং , A ও B সেট থেকে যথাক্রমে এমন কোন x , y খুঁজে পাওয়া যাবে না যাতে (x+y) একটি জোড় সংখ্যা হয় ।

সুতরাং , xRy ⇒ (x+y) –এর মান জোড় ,এই সম্মন্ধটি সম্ভব নয় ।

∴ A সেট থেকে B সেটে R সম্বন্ধটি একটি শূন্য সম্মন্ধ প্রকাশ করে ।

∴ R= Φ ,সুতরাং R একটি শূন্য সম্বন্ধ প্রকাশ করে ।

2 কখন কোন সেট A এর ওপর সংজ্ঞাত ও একটি সম্বন্ধ স্বসম নয় ? মনে করো A={a,b,c,d} এবং A উপর একটি সম্বন্ধ হলো R যেখানে R={(a,a),(a,c),(c,a),(c,c),(d,d)} A ওপর R কি স্বসম ?

সমাধানঃ R={(a,a),(a,c),(c,a),(c,c),(d,d)}এবং A={a,b,c,d}

A সেটের ওপর সংজ্ঞাত একটি সম্বন্ধ R ওই সেটে স্বসম হয় না যখন A সেটের অন্তর্গত কমপক্ষে একটি পদ a জন্য (a,a) ∉R হয়

এক্ষেত্রে ,{(a,a),(c,c),(d,d)}∈R হলেও , (b,b) ∉ R

∴ A এর সব a এর জন্য (a,a)∈R , এটি সিদ্ধ হচ্ছে না সুতরাং R সম্বন্ধটি স্বসম নয় ।

3 কখন কোন সেট A এর ওপর সংজ্ঞাত একটি সম্বন্ধ প্রতিসম নয় ? মনে করো X={1,2,3,4}এবং X এর ওপর একটি সম্বন্ধ R এর সংজ্ঞা হয় R = {(1,2),(3,4),(2,2),(4,3),(2,3)} , X এর ওপর R সম্বন্ধ কি প্রতিসম ?

সমাধান :

A সেটের ওপর সংজ্ঞাত একটি সম্বন্ধ R ওই সেটের উপর প্রতিসম হয় না যখন A সেটের অন্তর্গত দুটি স্বতন্ত্র পদ A ও B এমন হয় যে (a,b) ∈ R কিন্তু (b,a) ∉ R অথবা (b,a) ∈ R কিন্তু (a,b) ∉ R হয় ।

X={1,2,3,4}

R={(1,2),(3,4),(2,2),(4,3),(2,3)}

এক্ষেত্রে (1,2) ∈ R কিন্তু (2,1) ∉ R

আবার (2,3) ∈ R কিন্তু (3,2) ∉ R

∴ (a,b)∈ R ⇒ (b,a) ∈ R, এই শর্তটি সিদ্ধ হচ্ছে না সুতরাং R সম্বন্ধে টি প্রতিসম নয়

4.কখন কোন সেট এর ওপর সংজ্ঞাত একটি সম্বন্ধ বিপ্রতিসম নয়? মনে করো A={1,2,3,4} এবং A উপর একটি সম্বন্ধ R এর সংজ্ঞা হয় R={(1,1),(2,2),(3,4),(3,3),(2,1),(4,3)} A এর ওপর R কি বিপ্রতিসম ?

সমাধান :

A সেটের ওপর সংজ্ঞাত একটি সম্বন্ধ R ওই সেটের উপর বিপ্রতিসম হয়না যখন এ সেট এর অন্তর্গত দুটি স্বতন্ত্র পদ a ও b এমন হয় যে (a,b) ∈ R এবং (b,a) ∈ R

এক্ষেত্রে, (3,4) ∈ R এবং (4,3) ∈ R

যেহেতু 3 এবং 4 দুটি সতন্ত্র পদ

∴ সম্বন্ধ টি বিপ্রতিসম নয় ।

5. কখন কোন সেট A এর ওপর সংজ্ঞাত একটি সম্বন্ধ সঙ্ক্রমণ নয় ? মনে করো A এবং A ওপর একটি সম্বন্ধ R এর সঙ্গে হয় R= {(2,3),(1,2),(3,2),(4,1)} ,Aওপর R এর সম্বন্ধ কি সংক্রমণ ?

সমাধান :

একটি সম্বন্ধ R ওই সেটের ওপর সংক্রমণ হয় না যখন A সেটের অন্তত তিনটি পদ a ,b,c এমন হয় যে

(a,b) ∈ R এবং (b,c) ∈ R কিন্তু (a,c) ∉ R

এক্ষেত্রে (2,3) ∈ R এবং (3,2) ∈ R কিন্তু (2,2) ∉ R

∴ (a,b) ∈ R এবং(b,c) ∈ R কিন্তু (a,c) ∉ R

অতএব R সম্বন্ধ টি সংক্রমণ নয় ।

6. কোন সেট A এর উপর সংজ্ঞাত একটি সম্বন্ধ R একই সঙ্গে প্রতিসম এবং বিপ্রতিসম হতে পারে কি?

সমাধান :

কোন সেট A এর উপর একটি সম্বন্ধ R যদি (x,y) ∈ R ⇒ x=y আকারে সংজ্ঞাত হয় তবে A এর ওপর R সম্বন্ধ একইসঙ্গে প্রতিসম এবং বিপ্রতিসম হবে ।

উদাহরণ ঃ R ={ (2,2) , (3,3) , (4,4) }

এক্ষেত্রে (a,b) ∈ R ⇒ (b,a) ∈ R এই শর্তটি সিদ্ধ হচ্ছে এবং (a,b) ∈ R এবং (b,a) ∈ R ⇒ a=b এই শর্তটি ও সিদ্ধ হচ্ছে ।

∴ R সম্বন্ধে টি একই সাথে প্রতিসম এবং বিপ্রতিসম ।

7.ক্ষেত্র ও পাল্লা নির্ণয় করো :

(i) R₁={(a,1/a) :0<a<5 এবং a একটি অখণ্ড সংখ্যা }

এক্ষেত্রে a ={1,2,3,4}

∴ R₁= {(1,1),(2,1/2),(3,1/3),(4,1/4)}

∴ R₁ সম্বন্ধের ক্ষেত্র হবে {1,2,3,4} এবং পাল্লা হবে {1,1/2,1/3,1/4}

(ii) R₂₌{(x-y) : x ও y অখণ্ড সংখ্যা এবং xy=4}

∴ R₂={(1,4), (2,2) , (4,1), (-1,-4),(-2,-2),(-4,-1) }

∴ R₂এর ক্ষেত্র হবে {1,2,4,-1,-2,-4} এবং R ₂ পাল্লা হবে {1,2,4,-1,-2,-4}

(iii)R _{3 =}{x,y) : x∈N,y∈N এবং 2x+y=41}

∴ R ₃ ={1,39),(2,37),(3,35),……,(19,3),(20,1)}

এখন , 2x+y=41 ⇒ y=41-2x

∴ X এর মান যথাক্রমে 1,2,3,….,20 হলে y এর মান 39,37,35,…,3,1 হবে

∴ R₃এর ক্ষেত্র {1,2,3,…,19,20}

R₃এর পাল্লা {39,37,35,…,3,1}

(iv)R₄={ (x,y): xওy অখণ্ড সংখ্যা x²+y²=25 }

X²+y²=25

বা, y² = 25-x²

বা, y = √ (25-x²)

X এর মান এক্ষেত্রে -5,-4,-3,3,4,5 এগুলি হতে পারে যেহেতু x ওy অখণ্ড সংখ্যা

X এর মান যথাক্রমে -5,-4,-3,3,4,5 হলে y এর মান হবে 0,-3,-4,-5,3,4,5

∴ R ₄={(-5,0),(-4,-3),(-3,-4),(0,-5),(5,0),(4,3),(3,4),(0,5)}

∴ R ₄এরক্ষেত্র = R ₄ এর পাল্লা ={-5,-4,-3,0,3,4,5}

(v) R ₅={(x-5,2x-7): x হলও 10 এর কম একটি বিজোড় স্বাভাবিক সংখ্যা}

X এর মান বিজোড় সংখ্যা

∴ X = (1,3,5,7,9)

∴ R ₅= {(-4,-5),(-2,-1),(0,3),(2,7),(4,11)}

∴ R ₅এর ক্ষেত্র {-4,-2,0,2,4}

R ₅এর পাল্লা {-5,-1,3,7,11}

(vi)R₆={(x, x²-31) x হলও 12 এর কম মৌলিক সংখ্যা একটি মৌলিক সংখ্যা }

সমাধানঃ x হলও 12 এর কম একটি মৌলিক সংখ্যা

∴ x={2,3,5,7,11}

∴ R₆={(2,-27),(3,-22),(5,-6),(7,18),(11,90)}

∴ R₆এর ক্ষেত্র ={2,3,5,7,11}

∴ R ₆এর পাল্লা = {-27,-22,-6,18,90}

(vii) R={(x,y) : x একটি পূর্ণ সংখ্যা এবং |x|< 3 এবং y = |x-3| < 3}

X এর মান একটি পূর্ণসংখ্যা এবং |x|< 3

∴ X এর মান ={-2,-1,0,1,2}

R ={(-2,5),(-1,4),(0,3),(1,2),(2,1)}

∴ Rএর ক্ষেত্র ={ -2,-1,0,1,2}

R এর পাল্লা ={5,4,3,2,1}

(viii) s={(x,y) : x,y ∈ N এবং x+3y=12}

X+3y=12

Or, 3y=12-x

Or, y=(12-x)/3

∴ x এর মান ={3,6,9} হতে পারে

S={(3,3),(6,2),(9,1)}

∴ s এর ক্ষেত্র {3,6,9}

S এর পাল্লা ={3,2,1}

8. একটি সমতুল্যতা সম্বন্ধের সংজ্ঞা দাও । দেখাও যে কোনও সমতলে অঙ্কিত ত্রিভুজ সমূহের সেটের ওপরে সদৃশতা সম্বন্ধ একটি সমতুল্যতা সম্বন্ধ ।

সমাধানঃ

সমতুল্যতা সম্বন্ধ – শূন্য নয় এমন কোন সেট এর ওপর সংজ্ঞাত একটি সম্বন্ধ R কে A এর ওপর সমতুল্যতা সম্বন্ধে বলা হবে যদি (i) R সম্বন্ধ A এর ওপর স্বসম হয় অর্থাৎ সব a ∈A এর জন্য (a,a) ∈ R হয় । (ii) R সম্বন্ধ A এর ওপর প্রতিসম(symmetric) হয় অর্থাৎ সব (a,b) ∈ A এর জন্য (a,b) ∈ R ⇒ (b,a) ∈ R হয় ।এবং (iii) R সম্বন্ধ A ওপর সংক্রমণ হয় অর্থাৎ সব a,b,c ∈ A এর জন্য (a,b) ∈ R এবং (b,c) ∈ R ⇒ (a,c) ∈ R হয়।

(i) মনে করি , কোন সমতল এ অঙ্কিত ত্রিভুজ সমূহের সেট এর ওপর R সম্বন্ধ এরূপে সংজ্ঞাত যে

(∆₁,∆₂) ∈R ⇒ ∆₁ , ∆₂ এর সঙ্গে সদৃশ সব ∆₁,∆₂ ∈ ∆ এর জন্য

এখন সব ∆₁ এর জন্য (∆₁,∆₁) ∈R কারণ কোন ত্রিভুজ তার নিজের সঙ্গে সদৃশ

∴ R সম্পর্কটি স্বসম (Reflexive)

(ii) ধরা যাক, (∆₁,∆₂) ∈ ∆ এবং (∆₁,∆₂) ∈ R

অর্থাৎ ∆₁ , ∆₂ ত্রিভুজ দুটি সদৃশ

∴ ∆₂ ,∆₁ ত্রিভুজ দুটিও সদৃশ হবে ।

∴ (∆₁,∆₂) ∈ R ⇒ (∆₂,∆₁) ∈ R সব ∆₁,∆₂ ∈ ∆ এর জন্য

∴ R সম্বন্ধ টি প্রতসম ( symmetric)

(iii) ধরা যাক , (∆₁,∆₂) ∈ R এবং (∆₂,∆₃) ∈ R

∴ ∆₁ ও ∆₂ ত্রিভুজ দুটি সদৃশ ।

এবং ∆₂ ও ∆₁ ত্রিভুজ দুটি সদৃশ

∴ ∆₁ ও ∆₃ ত্রিভুজ দুটি ও সদৃশ হবে ।

∴ (∆₁,∆₃) ∈ R

∴ (∆₁,∆₂)∈ R এবং (∆₂,∆₃) ∈ R ⇒ (∆₁,∆₃) ∈ R সব ∆₁ , ∆₂ এবং ∆₃এর জন্য

∴ R সম্বন্ধ টি সঙ্ক্রমণ ( transitive).

∴ R সম্বন্ধে টি সমতুল্যতা সম্বন্ধ ।

9. A ={a,b,c} সেটের ওপর একটি সম্বন্ধে R এমনভাবে সংজ্ঞাত করো যাতে সম্বন্ধ টি স্বসম কিংবা প্রতিসম বা সংক্রমণ না হয় ।

সমাধান ঃ R = {(a,b) ,(b,c) , (c,a) }

এক্ষেত্রে (a,a) ∉ R (b,b) ∉ R এবং (c,c) ∉ R অর্থাৎ এক্ষেত্রে প্রত্যেক a ∈ A এর জন্য (a,a) ∈ A এই শর্তটি সিদ্ধ হচ্ছে না অতএব R সম্বন্ধ টি স্বসম নয় ।

আবার , (a,b) ∈ R হলে (b,a) ∉ R

অর্থাৎ (a,b) ∈ R ⇒ (b,a) ∈ R এই শর্তটি সিদ্ধ হচ্ছে না অতএব R সম্বন্ধে টি প্রতিসম নয়

আবার, (a,b) ∈ R এবং (b,c) ∈ R ⇒ (a,c) ∉ R

∴ R সম্বন্ধ টি সঙ্ক্রমন নয়

অর্থাৎ R সম্বন্ধ স্বসম , প্রতিসম এবং সংক্রমণ কোনোটিই নয় ।

10. মনে করো A={1,2,3} এবং এর ওপর R={(1,1),(2,3),(3,3)} একটি সম্বন্ধ এর সঙ্গে (i)সবচেয়ে কম (ii) সবচেয়ে বেশি সংখ্যক ক্রমিক জোড় যোগ করো যাতে পরিবর্ধিত সম্বন্ধ দুটি প্রত্যেকটি সমতুল্যতা সম্বন্ধ হয় ।

(i)সমাধানঃ

স্পষ্টতই প্রদত্ত সম্বন্ধ R সমতুল্যতা সম্বন্ধে হবে যদি এর ওপর R সম্বন্ধ স্বসম প্রতিসাম্ এবং সংক্রমণ হয় এখন দেখা যায় যে (1,1) ∈ R এবং(3,3) ∈ R সুতরাং (2,2) ∈ R হলে সম্পর্কটি স্বসম সম্বন্ধ হবে

আবার , (2,3) ∈ R কিন্তু (3,2) ∈ R সুতরাং A ওপর সম্বন্ধ টি প্রতসম হবে যদি (3,2) ∈ R হয়

∴ R={(1,1),(2,2),(3,3),(2,3),(3,2)}

∴ (2,3) ∈ R এবং (3,2) ∈ R ⇒ (2,2) ∈ R

∴R সম্বন্ধ টি সংক্রমণ সম্বন্ধ

উত্তরঃ সবচেয়ে কম (3,2) এবং (2,2) R এর সাথে যোগ করলে R সম্বন্ধ সমতুল্যতা সম্বন্ধ হবে ।

(ii) A×A ={(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)}

যদি R={(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)}হয় সেক্ষেত্রে স্পষ্টতই (1,1) ∈ R (2,2) ∈ R , (3,3) ∈ R

∴ প্রত্যেক a ∈ A এর জন্য (a,a) ∈ R শর্তটি সিদ্ধ হচ্ছে

∴ R সম্বন্ধ টি স্বসম সম্বন্ধ ।

আবার , (1,2) ∈ R এবং (2,1) ∈ R

(2,3) ∈ R এবং ( 3,2)∈ R

(1,3)∈ R এবং (3,1) ∈ R

∴ (a,b) ∈ R ⇒ (b,a) ∈ R এই শর্তটিও সিদ্ধ হচ্ছে

∴ R সম্বন্ধ টি প্রতিসম সম্বন্ধ ।

আবার , (1,2)∈ R এবং (2,1) ∈ R ⇒ (1,1)∈ R

(2,3) ∈ R এবং (3,2)∈ R ⇒ (2,2)∈ R

এবং (1,3) ∈ R এবং (3,1)∈ R ⇒ (1,1) ∈ R

∴ (a,b) ∈ R এবং (b,a) ∈ R ⇒ (a,a) ∈ R ,শর্তটি সিদ্ধ হচ্ছে

∴ R সম্বন্ধটি সংক্রমন সম্মন্ধ ।

দেখা যাচ্ছে R এর মধ্যে সর্বাপেক্ষা ক্রমিত জোড় {(2,2),(3,2),(1,2),(2,1),(3,1),(1,3)}

এইগুলি যোগ করলে R=A×A হয়

এবং R সম্বন্ধটি একটি সমতুল্যতা সম্বন্ধ হয় ।

11. মনে করো T₁ ,T₂ ,T₃তিন টি সমকোণী ত্রিভুজ যাদের তিনটি বাহু যথাক্রমে 3,4,5; 5,12,13 এবং 6,8,10 । T₁ T₂ এবং T₃ এর মধ্যে কারা সম্পর্কযুক্ত ?

সমাধান ঃ 3,4,5 এবং 6,8,10 বাহু বিশিষ্ট ত্রিভুজ দুটি পরস্পর সদৃশ কারণ এদের বাহু গুলি পরস্পর সমানুপাতিক ।

আবার , সদৃশতা একটি সমতুল্যতা সম্বন্ধ সুতরাং ত্রিভুজ দুটি পস্পর সমতুল্যতা সম্পর্ক যুক্ত ।

দুটি ত্রিভুজ এর সদৃশতা একটি সমতুল্যতা সম্পর্ক তা এই exercise এ অতিসংক্ষিপ্ত প্রশ্ন 8-এর অঙ্কে করে দেখান হয়েছে ।

আরও দেখুনঃ মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।

সংক্ষিপ্ত উত্তরধর্মী প্রশ্নঃ

1. দেখাও যে বাস্তব সংখ্যা সমূহের সেট এর উপর সংজ্ঞাত ‘‘অপেক্ষা বড়’’ সম্বন্ধ সংক্রমণ কিন্তু স্বসম বা প্রতিসম নয় ।

সমাধান ঃ

ধরা যাক R হল একটি বাস্তব সংখ্যার সেট এবং R সেটে সংজ্ঞাত একটি সম্বন্ধ R হলো x , y এর চেয়ে বড়(x>y) , x∈R এবং y∈R

এখন ধরা যাক , a ∈ R কিন্তু (a,a) ∉ R কারণ a তার নিজের থেকে বড় নয়

∴ R সম্বন্ধ স্বসম নয় ।

আবার, (a,b) ∈ R হলে (b,a) ∉ R কারণ a,b এর থেকে বড় হলে b,a থেকে বড় হতে পারেনা

∴ (a,b) ∈ R ⇏ (b,a) ∉ R

∴ R সম্পর্কটি প্রতিসম নয়

ধরা যাক a,b,c ∈ R

(a,b) ∈ R এবং (b,c) ∈ R

∴ a >b এবং b >c হলে স্পষ্টতই a >c

∴ (a,c) ∈ R

∴(a,b) ∈ R এবং (b,c) ∈ R ⇒ (a,c) ∈ R

∴ R সম্বন্ধ সংক্রমণ সম্বন্ধ ।

2.প্রমাণ করো যে কোন সমতল এ অঙ্কিত সরলরেখা সমূহের সেট L এর ওপর সংজ্ঞাত “ l₁ সরলরেখা l₂ এর উপর লম্ব l₁,l₂ ∈ L” সম্বন্ধ টি Lএর ওপর প্রতিসম কিন্তু স্বসম নয় ।

সমাধান ঃ

ধরা যাক প্রদত্ত সম্বন্ধ টি হলো R

∴ R = l₁ সরলরেখা l₂ এর উপর লম্ব

ধরি l₁∈L

এখন (l₁,l₁) ∈ R হতে পারে না

কারণ l₁ সরলরেখা তার নিজের সাথে লম্ব হতে পারে না

∴ l₁ এবং l₂ সরলরেখা পরস্পর লম্ব নয় ।

∴ (l₁,l₂) ∉ R

R সম্বন্ধ টি স্বসম নয় ।

ধরা যাক l₁,l₂ ∈ L এবং (l₁,l₂) ∈ R

∴ l₁, l₂ এর সাথে লম্ব

এর থেকে বলা যায় l₂ ,l₁ এর সাথে লম্ব

∴ (l₁,l₂) ∈ R ⇒ (l₂,l₁) ∈ R

∴ R সম্মন্ধ টি প্রতিসম ।

আবার , l₁,l₂,l₃ ∈ L

এবং (l₁,l₂) ∈ R অতএব l₁ ,l₂ এর ওপর লম্ব

(l₂,l₃) ∈ R অতএব l₂ , l₃ এর ওপর লম্ব

এ থেকে বলা যায় না যে l₁ , l₃ এর সাথে লম্ব

∴ (l₁,l₂) ∈ R এবং (l₂,l₃) ∈ R ⇏ (l₁,l₃) ∈ R

∴ R সম্পর্কটি সংক্রমণ নয় ।

3.স্বাভাবিক সংখ্যা সমূহের সেট N এর ওপর একটি সম্বন্ধ আর নিম্নরূপে সংজ্ঞাত { (x,y)∈R ⇒ y , x দ্বারা বিভাজ্য সব x,y ∈ N এর জন্য } দেখাও যে N এর ওপর R একটি সম্বন্ধ স্বসম এবং সঙ্ক্রমণ কিন্তু প্রতিসম নয়।

সমাধান ঃ x ∈ N

এবং x , x দ্বারা বিভাজ্য

∴ (x,x) ∈ R

সুতরাং R সম্বন্ধ টি স্বসম ।

আবার (x,y) ∈ N এবং (x,y) ∈ R অতএব y , x দ্বারা বিভাজ্য

y , x দ্বারা বিভাজ্য হলে x , y দ্বারা বিভাজ্য হবেই এটা বলা যাবে না যেহেতু x≠y

∴ (x,y) ∈ R ⇒ (y,x) ∈ R এই শর্ত টি সিদ্ধ হচ্ছে না

∴ R সম্বন্ধ টি প্রতিসম নয় ।

ধরাযাক x,y,z ∈ N

এবং (x,y) ∈ R , (y,z) ∈ R

∴ y , x দ্বারা বিভাজ্য এবং z,y দ্বারা বিভাজ্য

∴ z , x দ্বারা বিভাজ্য হবে। ।

∴ (x,y) ∈ R এবং (y,z) ∈ R ⇒ (x,z)∈ R

∴ R সম্বন্ধ টি সংক্রমণ এবং স্বসম সম্বন্ধ কিন্তু প্রতিসম নয় ।

আরও দেখুনঃ সৌরেন্দ্রনাথ দে দ্বাদশ শ্রেণির বইয়ের সকল অধ্যায়ের সমাধান

4 স্বাভাবিক সংখ্যা সমূহের সেট N এর ওপর একটি সম্বন্ধ R নিম্নরূপে সংজ্ঞাত(x,y) ∈ R ⇒ x+y=12 সব x,y ∈ N এর জন্য

প্রমাণ করো N এর ওপর R সম্বন্ধ প্রতিসম কিন্তু স্বসম কিংবা সংক্রমণ নয় ।

সমাধান : x,y ∈ N , x+y=12 ধরি x=1 এবং y=1

∴ 1+1=2 ≠12

R সম্বন্ধটির ক্ষেত্রে দেখা যায় যে, (1,1) ∉ R

সুতরাং সব a ∈ N এর জন্য (a,a) ∈ R এই শর্তটি সিদ্ধ হচ্ছে না অতএব N এর ওপর সংজ্ঞাত R সম্বন্ধ টি স্বসম নয় ।

আবার , (x+y) =12 ⇒ (y+x) = 12

∴ সব x,y ∈ N এর জন্য (x,y) ∈ R ⇒(y,x) ∈ R

∴ R সম্বন্ধ প্রতিসম হবে ।

আবার , (2,10) ∈ R কারণ 10+2 = 12

(10,2) ∈ R কারণ 2 +10 =12

কিন্তু (2,2) ∉ R কারণ 2+2 =4 ≠12

∴ (a,b)∈ R এবং (b,c) ∈ R ⇒(a,c) ∈ R , এই শর্তটি সিদ্ধ হচ্ছে না ।

∴ R সম্বন্ধটি সংক্রমন সম্মন্ধ নয় ।

5. স্বাভাবিক সংখ্যা সমূহের সেট N -এর ওপর একটি সম্মন্ধ R নিম্নরূপে সংজ্ঞাত:

(x,y)∈R ⇒ x+2y=10 ,x,y∈ N -এর জন্য । দেখাও যে ,N এর ওপর R সম্মন্ধ বিপ্রতিসম ।

সমাধানঃ R = {(x,y) : x+2y =10,x,y ∈ N }

ধরা যাক , (x,y)∈ R এবং (y,x)∈ R যেখানে x,y ∈ N

⇒ x+2y =10 এবং y+2x =10

⇒ x+2y =y+2x

⇒ x=y

∴ (x,y) ∊ R এবং (y,x) ∈ R ⇒ x = y ,যখন x ,y ∈ N

N -এর ওপর R সম্বন্ধটি বিপ্রতিসম সম্মন্ধ ।

6 মনে করো সব সাবসেট সমূহের সেট S এবং S এর ওপরে R সম্বন্ধের সংজ্ঞা x ⊆ y সব x,y ∈ s এর জন্য । দেখাও যে S ওপর R সম্বন্ধ স্বসম এবং সংক্রমণ কিন্তু প্রতিসাম্ নয় ।

সমাধান ঃ

ধরি , x ∈ S

স্পষ্টতই x ⊆ x কারণ প্রতিটি সেট তার নিজের সাথে সাবসেট

∴ S এর সব x এর জন্য (x,x) ∈ R

R সম্বন্ধ টি স্বসম ।

আবার , x,y ∈ S এবং x ⊆ y

কিন্তু x ⊆ y হলে y ⊆ x অসম্ভব (যেহেতু x≠y)

∴ (x,y) ∈ R হলেও (y,x)∉ R

∴ R সম্বন্ধ টি স্বসম হবে না।

আবার, ধরা যাক x,y,z ∈ S

যখন (x,y) ∈ R এবং (y,z) ∈ R

∴ x ⊆ y এবং y ⊆ z

∴ x ⊆ z

সুতরাং (x,y) ∈ R এবং (y,z) ∈ R ⇒ (x,z) ∈ R অতএব R সম্বন্ধ টি সঙ্ক্রমণ সম্বন্ধ ।

7 অখণ্ড সংখ্যা সমূহের সেট Z এর ওপর একটি সম্বন্ধ R নিম্নরূপে সংজ্ঞাত R={(x-y): x,y ∈ z এবং x-y জোড় সংখ্যা } প্রমাণ করো যে Z এর ওপর R সমতুল্যতা সম্বন্ধ ।

সমাধানঃ R=(x,y):x,y ∈ Z এবং (x-y)=2k ,k ∈ z}

সব x ∈ z এর জন্য , x-x=0 ⇒ (x,x) ∈ R সব x ∈ z এর জন্য ।

অতএব R সম্বন্ধ টি স্বসম ।—-(i)

ধরাযাক (x,y) ∈ R

⇒ x-y=2k , k ∈ Z

⇒ y-x =-2k= 2(-k) , -k ∈ Z

∴ (y,x) ∈ R

∴ (x,y) ∈ R ⇒ (y,x) ∈ R সব x,y ∈ Z এরজন্য

∴ R সম্বন্ধ টি প্রতিসম —–(ii)

ধরাযাক (x,y) ∈ R এবং (y,z) ∈ R

যেখানে x,y,z ∈ Z

∴ x-y =2k , k ∈ Z

এবং y-z=2m , m ∈ Z

∴ x-z=(x-y)+(y-z)=2k+2m=2(k+m)=2l [∵ k+m=l ∈Z]

⇒ (x,z)∈ R

∴ (x,y) ∈ R and (y,z) ∈ R ⇒ (x,z) ∈ R

∴R সম্বন্ধটি সংক্রমন সম্মন্ধ —(iii)

∴(i) ,(ii) এবং (iii) থেকে বলা যায়ে R সম্বন্ধ টি সমতুল্যতা সম্বন্ধ ।

8.(i)সব অখন্ড সংখ্যা সমূহের সেট Z এর ওপর একটি সম্বন্ধ R নিম্নরূপে সংজ্ঞাত ঃ (x,y)∈ R Þ(x-y) এর মান n এর দ্বারা বিভাজ্য দেখাও যে Z এর ওপর R একটি সমতুল্যতা সম্বন্ধ ।

সমাধান

(X,Y) ∈ R ⇒ X-Y এর মান n দ্বারা বিভাজ্য

এখন x ∈ z এবং (x,x)∈ R কারন x-x=0, যা n দ্বারা বিভাজ্য ।

অতএব সব x ∈ z এর জন্য (x,x) ∈ R হচ্ছে সুতরাং R সম্বন্ধ টি স্বসম।…(i)

আবার (x,y) ∈ z এবং (x,y) ∈ R অতএব x-y, n দ্বারা বিভাজ্য ।

স্পষ্টতই y-x ও n দ্বারা বিভাজ্য হবে ।

অতএব (x,y)∈ R ⇒ (y,x)∈ R

অতএব R সম্বন্ধ টি প্রতিসম । …(ii)

ধরাযাক x,y,z ∈ z এবং (x,y)∈ R ও (y,x) ∈ R

∴ (x-y) , n দ্বারা বিভাজ্য এবং (y-z) , n দ্বারা বিভাজ্য

ধরি , (x-y)=nk এবং (y-z)=nk₁যেখানে k এবং k₁দুটি অখণ্ড সংখ্যা ।

x-z=(x-y)+(y-z)=nk+ nk₁=n(k+k₁)=nk₂^,যেখানে k₂ও একটি অখণ্ড সংখ্যা ।

∴ (x-z) , n দ্বারা বিভাজ্য ।

∴ (x,z) ∈ R

সুতরাং (x,y) ∈R এবং (y,z)∈ R ⇒ (x,z) ∈ R

∴ R সম্বন্ধ টি সঙ্ক্রমণ সম্বন্ধ । …(iii)

∴ (i) ,(ii) এবং (iii) থেকে বলা যায়ে R সম্বন্ধ টি সমতুল্যতা সম্বন্ধ ।

8(ii)মনে করো সব বহুভুজের সেট A ; A টে সংজ্ঞাত R সম্বন্ধ হয় , R={(P₁,P₂): P₁ ও P₂ তে সমসংখ্যক বাহু আছে } দেখাও যে R একটি সমতুল্যতা সম্মন্ধ .3,4,5 বাহু বিশিষ্ট সমকোণী ত্রিভুজের সঙ্গে সম্পর্কযুক্ত A এর পদসমুহের সেট নির্ণয় করো ।

সমাধান ঃ এক্ষেত্রে স্পষ্টতই (P₁, P₁) ∈ R ,সব P₁∈ A -এর জন্য কারন P₁ এর বাহু সংখ্যা P₁ এর সাথে সমান ।

অতএব R সম্বন্ধ টি স্বসম ।——–(i)

আবার, (P₁, P₂) ∈ R ⇒ (P₂ , P₁)∈ R

কারণ P₁ এর বাহু সংখ্যা P₂ এর সাথে সমান হলে অবশ্যই P₂ এর বাহু সংখ্যা P₁ এর সাথে সমান হবে ।

অতএব R সম্বন্ধ টি প্রতিসম ।——– (ii)

ধরাযাক P₁, P₂, P₃ ∈ A

এবং (P₁, P₂) ∈ R ও (P₂,P₃)∈ R

অর্থাৎ P₁, P₂ এর বাহু সংখ্যা সমান এবং P₂, P₃ এর বাহু সংখ্যা সমান ।

অবশ্যই P₁ ও P₃ এর বাহু সংখ্যা সমান হবে

∴ (P₁, P₃)∈ R

∴ R সম্বন্ধ টি সঙ্ক্রমণ ।—–(iii)

∴ (i) ,(ii) এবং (iii) থেকে বলতে পারি R সম্বন্ধ টি সমতুল্যতা সম্বন্ধ ।

9.নয় মনে করো কোন সমতলে O হল মূলবিন্দু এবং P ও Q ওই সমতলের অন্য দুটি বিন্দু Pও Q এরমধ্যে S সম্বন্ধে এমনভাবে সংজ্ঞাত করা হলো যাতে OP=OQ হয় দেখাও যে সংজ্ঞাত S সম্বন্ধ একটি সমতুল্যতা সম্বন্ধ ।

সমাধান ঃ কোনও সমতলে O হল মূলবিন্দু এবং P হল অন্য কোন একটি বিন্দু

এখন OP=OP ( সর্বদা সত্য )

ওই সমতলে সব বিন্দু P এর জন্য OP=OP হবে অর্থাৎ (P,P) ∈ S

∴ S সম্বন্ধ টি স্বসম —–(i)

আবার ওই একই সমতলে দুটি বিন্দু P ও Q এমনভাবে নেওয়া হল যাতে OP=OQ হয়

এখন OP=OQ ⇒ OQ=OP

অতএব (P,Q) ∈ S Þ(Q,P)∈ S

∴ R সম্বন্ধ টি প্রতিসম সম্বন্ধ—–(ii)

ওই তিনটি বিন্দু P ,Q,R এমনভাবে নেওয়া হল যেন (P,Q) ∈ S এবং (Q,R) ∈ S হয়

∴ OP=OQ এবং OQ=OR ⇒ OP=OR

∴ (P,R) ∈ S

সুতরাং (P,Q) ∈ S এবং (Q,R) ∈ S ⇒ (P,R) ∈ S

S সম্বন্ধ টি সঙ্ক্রমণ সম্বন্ধ ।—-(iii)

(i) (ii) (iii) থেকে বলা যায় S সম্বন্ধ টি সমতুল্যতা সম্বন্ধ ।

আরও দেখুনঃ সৌরেন্দ্রনাথ দে দ্বাদশ শ্রেণির বইয়ের সকল অধ্যায়ের সমাধান

10.বাস্তব সংখ্যার সেট R এর ওপরে একটি সেট S নিম্নরুপে সংজ্ঞাত

S={(x,y):x,y ∈ R এবং X=±Y} দেখাও যে R এর ওপর S একটি সমতুল্যতা সম্বন্ধ ।

সমাধান

সমস্ত বাস্তব সংখ্যা x এর জন্য x=+x এটি সত্য

∴ (x,x)∈ S সব x ∈ R -এর জন্য ।

∴ S সম্বন্ধ টি স্বসম ——–-(i)

আবার x,y ∈ R এবং x= ± y

x=± y ⇒ y= ± x

∴ (x,y)∈ S ⇒ (y,x) ∈ S

∴ S সম্বন্ধ টি প্রতিসম ।———(ii)

ধরা যাক , x,y,z ∈ R এবং (x,y)∈ S ও (y,z)∈ S

∴ x= ± y এবং y= ± z

স্পষ্টতই x= ± z অতএব (x,z) ∈ S

সুতরাং (x,y) ∈ S ও (y,z) ∈ S ⇒ (x,z) ∈ S

S সম্বন্ধ টি সঙ্ক্রমণ সম্বন্ধ ।———(iii)

(i) ,(ii) , এবং (iii) থেকে পাই S সম্বন্ধ টি সমতুল্যতা সম্বন্ধ ।

11. একটি প্রদত্ত সেট A এর ওপর ক্ষুদ্রতম এবং বৃহত্তম সমতুল্যতা সম্মন্ধের সংজ্ঞা দাও ।

সমাধান A সেটের ওপর ক্ষুদ্রতম সমতুল্যতা সম্বন্ধ হলও সেই সম্বন্ধ টি যা একটি সমতুল্যতা সম্বন্ধ এবং সকল সমতুল্যতা সম্মন্ধের মধ্যে ক্ষুদ্রতম ।

I_A={(x,x) : x ∈ A} সম্বন্ধ টি A সেটের ওপর ক্ষুদ্রতম সমতুল্যতা সম্বন্ধ ।

A সেটের ওপর বৃহত্তম সমতুল্যতা সম্বন্ধ হলও সেই সম্বন্ধ টি যা একটি সমতুল্যতা সম্বন্ধ এবং সকল সমতুল্যতা সম্মন্ধের মধ্যে বৃহত্তম ।

A×A ={(x,y) : x ,y ∈ A }

12 বাস্তব সংখ্যা সমূহের সেট R এর ওপর একটি সম্বন্ধ নিম্নরূপে সংজ্ঞাত S={(x,y) :x²+y²=1 সব x,y ∈ R এর জন্য }R এর ওপর S সম্বন্ধটির (i) স্বসমতা (ii) প্রতিসাম্যতা (iii) সংক্রমিতা পরীক্ষা করো ।

সমাধানঃ S = {(x,y): x²+y² =1 , x,y ∈ ℝ }

(1,1) ∉ S [ যেহেতু 1²+1² =1 ≠1]

∴ S স্বসম নয় ।

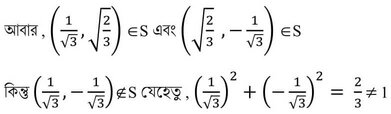
SN Dey Math Solution Of Class 12 Chapter 1 Relation

∴ S সম্বন্ধটি সংক্রমন নয় ।

ধরা যাক , (x,y) ∈ S

⇒ x²+y² =1 ⇒ y²+x²=1 ⇒ (y,x)∈ S

∴ (x,y) ∈ S Þ (y,x) ∈ S for all x ,y ∈ ℝ

সুতরাং S সম্বন্ধটি প্রতিসম সম্মন্ধ ।

13 মনে করো A ={a,b,c} একটি প্রদত্ত সেট এর ওপর একটি সম্বন্ধ এমনভাবে সংজ্ঞাত করো যাতে A ওপর সম্বন্ধ টি

(i)স্বসম এবং সংক্রমণ হয় কিন্তু প্রতিসম না হয়

(ii) স্বসম এবং প্রতিসম হয় কিন্তু সংক্রমণ না হয় ।

(iii) প্রতিসম এবং সংক্রমণ হয় কিন্তু স্বসম না হয় ।

(iv) স্বসম কিন্তু প্রতিসম কিম্বা সংক্রমণ না হয় ।

(v) প্রতিসম কিন্তু স্বসম কিংবা সংক্রমণ না হয় ।

(vi) সংক্রমণ কিন্তু স্বসম কিংবা প্রতিসম না হয় ।

(vii) স্বসম কিংবা প্রতিসম বা সংক্রমণ না হয় ।

(viii)একটি সমতুল্যতা সম্বন্ধ হয় ।

সমাধান

A একটি প্রদত্ত সেট যেখানে A={a,b,c}

ধরা যাক A সেটের ওপর একটি সম্বন্ধ R₁ হলো

R1={(a,a),(b,b),(c,c),(a,b),(b,c),(a,c)}

স্বসমতা – সব a এর জন্য (a,a)∈R₁

সুতরাং R₁ সম্বন্ধ স্বসম সম্বন্ধ

সংক্রমিতা- সব a,b,c ∈ A এর জন্য (a,b) ∈ R₁ এবং (b,c)∈ R₁ ⇒ (a,c)∈ R₁

সুতরাং A সেটের ওপর R₁ সম্বন্ধ টি সংক্রমণ সম্বন্ধ

প্রতিসাম্যতা- (a,b)∈ R₁ কিন্তু (b,a) ∉ R₁

অর্থাৎ aR₁b কিন্তু bR₁a সুতরাং R₁ সম্বন্ধ টি প্রতিসাম্য নয় ।

(ii)ধরা যাক A সেটের ওপর R₂ সম্বন্ধ নিম্নরূপে সংজ্ঞাত R₂={(a,a),(b,b),(c,c),(a,b),(b,a),(b,c),(c,b)}

স্বসমতা- সব a ∈ A এর জন্য (a,a)∈ R₂ সুতরাং A সেটের ওপর R₂ সম্বন্ধ টি স্বসম

প্রতিসাম্যতা-সব a,b ∈ A এর জন্য (a,b)∈ R₂ ⇒ (b,a)∈ R₂

সুতরাং A সেটের ওপর R₂ সম্বন্ধ টি প্রতিসম

সংক্রমিতা- সব a,b,c ∈ A এর জন্য (a,b)∈ R₂এবং (b,c)∈ R₂ কিন্তু (a,c)∉R₂

সুতরাং R₂ সম্বন্ধ টি সংক্রমণ নয়

(iii) ধরা যাক A সেটের ওপর R₃ সম্বন্ধ টি নিম্নরূপে সংজ্ঞাত R₃={(a,b),(b,a),(a,a)}

স্বসমতা – b ∈ A কিন্তু (b,b) ∉ R₃ সুতরাং A সেটের ওপর R₃ সম্বন্ধ টি স্বসম নয় ।

প্রতিসাম্যতা – (a,b) ∈ R₃⇒ (b,a) ∈ R₃

সুতরাং A সেটের ওপর R₃ সম্বন্ধ টি প্রতিসম সম্বন্ধ ।

সংক্রমিতা – (a,b) ∈ R₃ এবং (b,a)∈ R₃ ⇒ (a,a) ∈ R₃ সুতরাং A সেটের ওপর R₃ সম্বন্ধটি সংক্রমণ

(iv)ধরা যাক A সেটের ওপর R₄ সম্বন্ধ টি নিম্নরূপে সংজ্ঞাত R₄={(a,a),(a,b),(b,b),(b,c),(c,b),(c,c)}

স্পষ্টতই R স্বসম কারণ (a,a)∈R₄ ,(b,b)∈R₄ এবং (c,c)∈R₄

(a,b) ∈ R₄ কিন্তু (b,a)∉ R₄⇒ R₄ সঙ্ক্রমণ নয় ।

(a,b) ∈ R₄এবং (b,c) ∈ R₄ কিন্তু (a,c) ∉ R₄

∴ R₄ সম্বন্ধ টি সঙ্ক্রমণ নয় ।

(v) ধরা যাক R₅={(a,b),(b,a),(b,c),(c,b)}

স্পষ্টতই R₅ সম্বন্ধ টি প্রতিসম কারণ (a,b) ∈ R₅⇒(b,a) ∈ R₅

আবার (b,c) ∈ R₅ ⇒ (c,b) ∈ R₅

(a,a) ∉ R₅ ⇒ R₅ স্বসম নয়

(a,b) ,(b,c) ∈ R₅ কিন্তু (a,c) ∉ R₅

∴ R₅ সম্বন্ধ টি সঙ্ক্রমণ নয় ।

(vi) ধরা যাক R₆={(a,b),(b,b)}

(a,b),(b,b) ∈ R6 ⇒(a,b)∈ R₆

অতএব R₆ সঙ্ক্রমণ সম্বন্ধ

(a,a) ∉ R₆ , অতএব R₆ স্বসম নয় ।

(a,b) ∈ R₆ কিন্তু (b,a) ∉ R₆ অতএব R₆ প্রতিসম নয় ।

(vii) ধরা যাক R₇={(a,b),(b,c),(c,a)}

R₇ স্বসম নয় যেহেতু (a,a) ∉ R₇

R₇ প্রতিসম নয় যেহেতু (a,b) ∈ R₇ কিন্তু (b,a) ∉ R₇

R₇ সঙ্ক্রমণ নয় যেহেতু (a,b) ,(b,c) ∈ R কিন্তু (a,c)∉ R₇

(viii)ধরা যাক R₈= A×A

স্পষ্টতই R₈ সম্বন্ধ টি একটি সার্বিক সম্বন্ধ অতএব R₈ সম্বন্ধ টি একটি সমতুল্যতা সম্বন্ধ ।

14.স্বাভাবিক সংখ্যা সমূহের সেট N এর ওপর একটি সম্বন্ধ N নিম্নরুপে সংজ্ঞাত হয় ঃ

R={(x,y): x∈N ,y∈N এবং x,y এর গুণিতক । দেখাও যে N এর ওপর R সম্বন্ধ টি স্বসম ,সঙ্ক্রমণ কিন্তু প্রতিসম নয় ।

সমাধান

x∈ N , x ,x এর গুণিতক যেহেতু x ×1=x

∀ x∈N (x,x)∈R

অতএব R সম্বন্ধ টি স্বসম ।

ধরাযাক (x,y)∈ R এবং (y,x)∈ R

x =yk এবং y=xm যেখানে k,m ∈ N

এখন y=xm

⇒ y=(yk)m

⇒ y=y(km)

⇒ km=1

⇒ k=m=1

∴ x=y

(x,y)∈R এবং (y,x)∈ R ⇒ x=y

∴ R সম্বন্ধ টি বিপ্রতিসম

এখন ধরা যাক , (x,y) ∈ R এবং (y,z) ∈ R যেখানে x,y,z ∈ N

x=yk এবং y=zl , যেখানে k ,l ∈ N

এখন, x=yk ⇒ x=(zl)k ⇒ x=z(lk) ⇒ x=zp , যেখানে p=lk ∈ N

∴ (x,z)∈ R

∴ (x,y)∈ R এবং (y,z)∈ R ⇒ (x,z)∈ R

∴ R সম্বন্ধ টি সঙ্ক্রমণ সম্বন্ধ ।

স্পষ্টতই (6,3)∈ R কিন্তু (3,6)∈ R

সুতরাং R সম্বন্ধ টি প্রতিসম নয় ।

15.মনে করো একটি সেট A এর ওপর R ও S দুটি সম্বন্ধ যদি

(i) R এবং S উভয় A এর ওপর প্রতিসম হয় তবে প্রমান করো যে R∪S এবং R∩S উভয় A এর ওপর প্রতিসম হবে ।

(ii) R স্বসম এবং S যেকোনো একটি সম্বন্ধ হলে প্রমান করো যে R∪S সম্বন্ধ A এর ওপর স্বসম হবে ।

(iii)R ও S উভয় A এর ওপর সঙ্ক্রমণ হয় তবে প্রমান করো যে R∩S সম্বন্ধ A এর ওপর সঙ্ক্রমণ হবে ।কিন্তু R∪S সম্মন্ধ A এর ওপর সঙ্ক্রমণ নাও হতে পারে ।

সমাধান (i) ধরা যাক, (x,y) ∈ R∪S যেখানে x,y ∈ A

⇒ (x,y)∈ R or (x,y)∈ S

এখন , (x,y)∈ R ⇒ (y,x) ∈ R [ যেহেতু , R প্রতিসম ]

⇒ (y,x) ∈ R∪S

∴ (x,y) ∈ R∪S ⇒ (y,x) ∈ R∪S

∴ R ∪ S সম্বন্ধ টি একটি প্রতিসম সম্বন্ধ ।

এখন ধরা যাক, (x,y) ∈ R∩S যেখানে x,y ∈ A

⇒ (x,y)∈ R এবং (x,y) ∈ S

⇒ (y,x)∈ R এবং (y,x)∈ S

⇒ (y,x) ∈ R∩S

∴ (x,y) ∈ R∩S Þ(y,x)∈ R∩S , সব x,y ∈ R∩S -এর জন্য।

সুতরাং , R∩S একটি প্রতিসম সম্বন্ধ ।

(ii) যেহেতু, A সেটের ওপর R একটি স্বসম সম্বন্ধ,

সুতরাং, (x,x)∈ R, সব x ∈A এর জন্য ।

⇒ (x,x)∈ R∪S , সব x ∈ A এর জন্য , যেকোনো সম্বন্ধ S এর জন্য

⇒ R∪S সম্বন্ধ A এর ওপর স্বসম ।

(iii) ধরা যাক , (x,y) ,(y,z) ∈ R ∩ S

এখানে x,y,z ∈ A

⇒ (x,y), (y,z)∈ R এবং

(x,y), (y,z)∈ S

⇒ (x,z) ∈ R এবং (x,z)∈ S, [ যেহেতু R ও S উভয়েই সংক্রমণ ]

⇒ (x,z) ∈ R ∩ S

∴ R Ç S সম্মন্ধ A এর ওপর সঙ্ক্রমণ ।

এখন ধরা যাক ,x,y,z ∈ A এমন তিনটি পদ যে ,

(x,y) ∈ R , (y,z) ∈ S কিন্তু (x,z) ∉ R এবং (x,z) ∉ S

সেক্ষেত্রে , (x,y) ,(y,z) ∈ R∪S

কিন্তু (x,z) ∉ R∪S

∴ R∪S সম্বন্ধ A এর ওপর সঙ্ক্রমণ নাও হতে পারে ।

16. স্বাভাবিক সংখ্যা সমূহের সেট N এর ওপর একটি সম্বন্ধ R নিম্নরুপে সংজ্ঞাত হয়ঃ

(x,y)∈R ⇒ x-y+√3 একটি অমূলদ সংখ্যা , সব x,y ∈ N এর জন্য দেখাও যে N এর ওপর R সম্বন্ধ স্বসম ।

সমাধান

R ={(x,y):x-y+√3 ∈ R-Q ,x,y ∈ N}

∀ x ∈ N ,(x,x)∈ R যেহেতু , x-x+√3=√3 ∈ R-Q

অতএব N এর ওপর R একটি স্বসম সম্বন্ধ ।

আরও দেখুনঃ মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধান

আরও দেখুনঃ সৌরেন্দ্রনাথ দে দ্বাদশ শ্রেণির বইয়ের সকল অধ্যায়ের সমাধান

আরও দেখুনঃ WBCHSE Official Site

আরও দেখুনঃ উচ্চমাধ্যমিক ক্লাস ১২ এর সকল বিষয়ের মক টেস্ট

SN Dey Math Solution Of Class 12 Chapter 1 Relation

অতিসংক্ষিপ্ত প্রশ্নাবলীঃ

সংক্ষিপ্ত উত্তরধর্মী প্রশ্নঃ

ধন্যবাদ । এই POST টি ভালো লাগলে SHARE করার অনুরোধ রইল । এইরকম আরও সুন্দর সুন্দর POST পেতে , আমাদের FACEBOOK PAGE টি LIKE করুন ।

Leave a Comment Cancel reply