বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য কষে দেখি ১০|কষে দেখি ১০ ক্লাস ১০|Koshe Dekhi 10 Class10|গণিত প্রকাশ সমাধান দশম শ্রেণি (ক্লাস ১০)(টেন)|WBBSE Madhyamik Class 10(Ten)(X) Math Chapter 10 Solution|WB Board Maths Solution Class 10| Ganit Prakash Somadhan Class 10.
মাধ্যমিক গণিত প্রকাশ বইএর সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
প্রশ্নঃ বৃত্তস্থ চতুর্ভুজ কাকে বলে ?
উত্তরঃ যে চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক তাকে বৃত্তস্থ চতুর্ভুজ বলে ।
প্রশ্নঃ সম্পূরক কোন কাকে বলে?
উত্তরঃ কোনো দুটি কোণের সমষ্টি 2 সমকোন হলে একটি কোন, অপর কোনটির সাথে সম্পূরক বলা হয় ।
বৃত্তস্থ চতুর্ভুজের কিছু গুরুত্বপূর্ণ ধর্মঃ
(i) বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক ।
(ii) একটি বৃত্তস্থ চতুর্ভুজের কোনো একটি বাহুকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোন, অন্তঃস্থ বিপরীত কোনের সমান ।( প্রমান গণিত প্রকাশ বই-এ আছে )
(iii) বৃত্তস্থ সামান্তরিক সর্বদা আয়তক্ষেত্র হবে । ( প্রমান গণিত প্রকাশ বই-এ আছে )
(iv) বৃত্তস্থ ট্রাপিজিয়াম অবশ্যই সমদ্বিবাহু ট্রাপিজিয়াম হবে ।( প্রমান গণিত প্রকাশ বই-এ আছে)
বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য কষে দেখি ১০|Koshe Dekhi 10 Class 10|কষে দেখি 10 ক্লাস 10
1. পাশের ছবির PQRS বৃত্তস্থ চতুর্ভুজের কর্নদ্বয় পরস্পরকে X বিন্দুতে এমন ভাবে ছেদ করেছে যে , ∠PRS = 65∘ এবং ∠RQS = 45∘ ; ∠SQP ও ∠RSP এর মান হিসাব করে লিখি ।

সমাধানঃ
∠SQP = ∠PRS [ একই বৃত্তাংশস্থ সকল কোণের মান সমান ]
∴ ∠SQP = 65º
∠SQR = ∠SPR [একই বৃত্তাংশস্থ সকল কোণের মান সমান ]
∴ ∠SPR = 45º
∴ ∆SPR এর ক্ষেত্রে ,
∠PSR = 180º-(∠SPR+∠SRP)
= 180º-(45º+65º)
= 180º-110º
= 70º
∴ ∠RSP = 70º
বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য কষে দেখি ১০|কষে দেখি ১০ ক্লাস ১০|Koshe Dekhi 10 Class10
2.ABCD বৃত্তস্থ চতুর্ভুজের AB বাহুকে X বিন্দু পর্যন্ত বর্ধিত করলাম এবং মেপে দেখেছি ∠XBC = 82º এবং ∠ADB=47º ; ∠BAC এর মান হিসাব করে লিখি ।
সমাধানঃ

∠XBC = 82º
∴ ∠ABC = 180º-82º= 98º
∴ ∠ADC = 180º-98º=82º [ ∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক ]
∴ ∠ADB+∠BDC = 82º
বা, 47º+∠BDC=82º
বা, ∠BDC = 82º-47º
বা, ∠BDC =35º
∴ ∠BAC = 35º [ একই বৃত্তাংশস্থ সকল কোনের মান সমান ]
বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য কষে দেখি ১০|কষে দেখি ১০ ক্লাস ১০|Koshe Dekhi 10 Class10
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
3. PQRS বৃত্তস্থ চতুর্ভুজের PQ , SR বাহুদুটি বর্ধিত করায় T বিন্দুতে মিলিত হল । বৃত্তের কেন্দ্র O ; ∠POQ =110º , ∠QOR =60º ,∠ROS = 80º হলে , ∠RQS ও ∠QTR এর মান হিসাব করে লিখি ।
সমাধানঃ
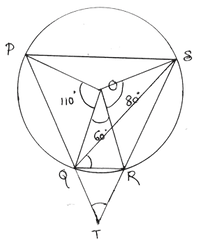
RS বৃত্তচাপের ওপর ∠ROS কেন্দ্রস্থ কোন এবং ∠RQS পরিধিস্থ কোন ।
∴ ∠RQS = ½ ∠ROS = ½✕ 80º = 40º [∵একই বৃত্তচাপের ওপর অবস্থিত কেন্দ্রস্থ কোন পরিধিস্থ কোনের দ্বিগুন ]
∴ ∠RQS = 40º
∠QSR = ½ ∠QOR [ ∵ QR বৃত্তচাপের ওপর কেন্দ্রস্থ কোন ∠QOR এবং পরিধিস্থ কোন ∠QSR, একই বৃত্তচাপের ওপর অবস্থিত কেন্দ্রস্থ কোন পরিধিস্থ কোনের দ্বিগুন]
∠QSR = ½✕ 60º
∠QSR = 30º
∠POS = 360º-(∠POQ+∠QOR+∠ROS)
∠POS=360º-(110º+60º+80º)
∠POS=360º-250º
∠POS=110º
PS বৃত্তচাপের ওপর ∠POS কেন্দ্রস্থ কোন এবং ∠PQS পরিধিস্থ কোন ।
∴ ∠PQS = ½ ∠POS [ ∵ একই বৃত্তচাপের ওপর অবস্থিত কেন্দ্রস্থ কোন পরিধিস্থ কোনের দ্বিগুন ]
∠PQS= ½ ✕110º = 55º
আবার ∆SQT এর বহিঃস্থ কোন ∠PQS = ∠QST+∠QTS [ ∵ ত্রিভুজের কোনো একটি বাহুকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোন অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান ]
∴ 55º = 30º+∠QTS
বা, ∠QTS = 55º-30º
বা, ∠QTS = 25º
∴ ∠QTR = 25º [ ∵ ∠QTR =∠QTS]
বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য কষে দেখি ১০|কষে দেখি ১০ ক্লাস ১০|Koshe Dekhi 10 Class10
4. দুটি বৃত্ত পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে । P ও Q বিন্দুগামী দুটি সরলরেখা একটি বৃত্তকে যথাক্রমে A ও C বিন্দুতে এবং অপর বৃত্তকে B ও D বিন্দুতে ছেদ করেছে । প্রমাণ করি যে AC ∥ BD ।
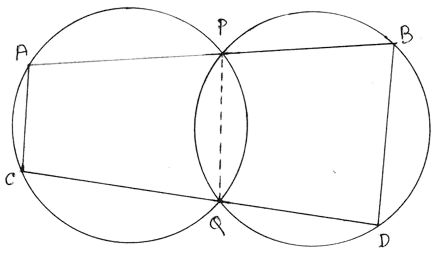
দুটি বৃত্ত পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে । P এবং Q বিন্দু দিয়ে অঙ্কিত দুটি সরলরেখা বৃত্তদুটিকে যথাক্রমে A,C ও B,D বিন্দুতে ছেদ করেছে । প্রমাণ করতে হবে যে , AC ∥BD ।
অঙ্কনঃ P ও Q যুক্ত করা হল ।
প্রমানঃ ACQP বৃত্তস্থ চতুর্ভুজ ।
∴ ∠ACQ +∠APQ = 180º [∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক ]
আবার , AB সরলরেখার ওপর P বিন্দুতে PQ সরলরেখা দণ্ডায়মান , তাই ,
∠APQ+∠BPQ = 180º [ এক সরল কোন ]
∴ ∠ACQ+∠APQ = ∠APQ+∠BPQ
∠ACQ = ∠BPQ
আবার , PQDB বৃত্তস্থ চতুর্ভুজের ক্ষেত্রে ,
∠BDQ + ∠BPQ = 180º [ ∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক ]
∠BDQ+∠ACQ = 180º [ ∠BPQ = ∠ACQ ]
এখন , AC ও BD সরলরেখাকে , CD ভেদক ছেদ করায় একই পার্শ্বস্থ অন্তঃকোণ ∠BDQ ও ∠BCQ উৎপন্ন হয় এবং এদের সমষ্টি 2 সমকোণ ।
∴ AC ∥ BD [প্রমাণিত ]
বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য কষে দেখি ১০|কষে দেখি ১০ ক্লাস ১০|Koshe Dekhi 10 Class10
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
5. ABCD একটি বৃত্তস্থ চতুর্ভুজ অঙ্কন করেছি এবং BC বাহুকে E পর্যন্ত বর্ধিত করলাম ।প্রমাণ করি যে , ∠BAD ও ∠DCE এর সমদ্বিখণ্ডকদ্বয় বৃত্তের ওপর মিলিত হবে ।

মাধ্যমিক গণিত প্রকাশ বইএর সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
6. মোহিত একটি বৃত্তের বহিঃস্থ বিন্দু x দিয়ে দুটি সরলরেখা অঙ্কন করেছে যারা বৃত্তটিকে যথাক্রমে A ,B বিন্দু ও C ,D বিন্দুতে ছেদ করেছে । যুক্তি দিয়ে প্রমাণ করি যে , ∠XAC ও ∠XBD এর দুটি করে কোন সমান ।
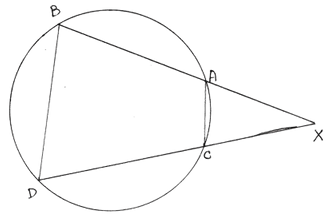
বৃত্তের বহিঃস্থ বিন্দু X দিয়ে দুটি সরলরেখা টানা হয়েছে , যারা বৃত্তটিকে যথাক্রমে A ,B বিন্দু এবং C,D বিন্দুতে ছেদ করেছে ।
প্রমাণ করতে হবে যে , ∠XAC = ∠XBD
অঙ্কন ঃ B,D ও A,C যুক্ত করা হল ।
প্রমানঃ ABDC একটি বৃত্তস্থ চতুর্ভুজ ।
∴ ∠BDC +∠BAC = 180º [ ∵বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক ]
আবার , ∠BAC + ∠XAC = 180º [ এক সরলকোণ = 180º ]
∴ ∠BDC+∠BAC = ∠BAC+∠XAC
বা, ∠BDC = ∠XAC
∴ ∆XAC ও ∆XBD এর দুটি করে কোন সমান [প্রমাণিত ]।
7. দুটি বৃত্ত অঙ্কন করেছি যারা পরস্পরকে G ও H বিন্দুতে ছেদ করেছে । এবার G বিন্দুগামী একটি সরলরেখা অঙ্কন করলাম যেটি বৃত্ত দুটিকে P ও Q বিন্দুতে এবং H বিন্দুগামী PQ – এর সমান্তরাল অপর একটি সরলরেখা অঙ্কন করলাম যা বৃত্ত দুটিকে R ও S বিন্দুতে ছেদ করল । প্রমাণ করি যে PQ = RS ।
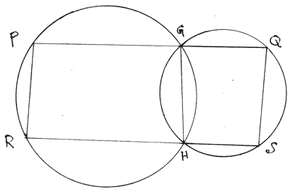
অঙ্কনঃ P,R ; G, H এবং Q ,S যুক্ত করা হল ।
প্রমানঃ GHSQ বৃত্তস্থ চতুর্ভুজের ক্ষেত্রে ,
∠HSQ+∠HGQ = 180º
আবার ,PS সরলরেখার ওপর G বিন্দুতে , GH দণ্ডায়মান ,
∴ ∠PGH+∠HGQ = 180º
∴ ∠HSQ+∠HGQ = ∠PGH+∠HGQ
বা , ∠HSQ= ∠PGH
আবার , PRHG বৃত্তস্থ চতুর্ভুজের ক্ষেত্রে ,
∠PRH + ∠PGH = 180º
∴ ∠PRH+ ∠HSQ = 180º [ ∠PGH = ∠HSQ ]
∴ PR ও QS বাহুদ্বয়ের ভেদক RS এর একই পার্শ্বস্থ অন্তঃকোণের সমষ্টি 180º
∴ PR ∥ QS
আবার , PQ ∥ RS
∴ PRSQ একটি সামান্তরিক ।
∴ PQ = RS [প্রমাণিত ]
বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য কষে দেখি ১০|কষে দেখি ১০ ক্লাস ১০|Koshe Dekhi 10 Class10
8. ABC একটি ত্রিভুজ অঙ্কন করেছি যার AB = AC এবং বর্ধিত BC এর ওপর E যেকোনো একটি বিন্দু । ∆ABC এর পরিবৃত্ত AE কে D বিন্দুতে ছেদ করলে প্রমাণ করি যে , ∠ACD = ∠AEC ।
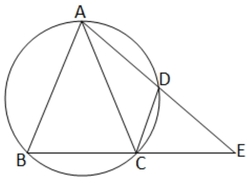
প্রমাণ ঃ ABCD একটি বৃত্তস্থ চতুর্ভুজ ।
∠ABC +∠ADC = 180º [ ∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক ]
আবার , ∠ADC +∠EDC = 180º [ ∵ CD সরলরেখা , AE সরলরেখার ওপর দণ্ডায়মান ]
∴ ∠ABC +∠ADC = ∠ADC +∠EDC
∠ABC = ∠EDC
∠ABC = ∠CDE—–(i)
আবার , ABC এর AB =AC
∴ ∠ABC = ∠ACB —– (ii)
CDE এর EC বাহু B পর্যন্ত বর্ধিত ,
∴ ∠DCB = ∠CDE+∠CED [ ∵ ত্রিভুজের কোনো একটি বাহুকে বর্ধিত করলে যে বহিঃস্থ কোন উৎপন্ন হয় তা অন্তঃস্থ বিপরীত কোণদ্বয়ের সমস্টির সমান ]
∠ACD+∠ACB = ∠ABC+∠CED [ ∵ (i) থেকে পাই ∠ABC = ∠CDE ]
∠ACD = ∠CED [ ∵ (ii) থেকে পাই ,∠ACB = ∠ABC]
∴ ∠ACD = ∠AEC [প্রমাণিত ]
বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য কষে দেখি ১০|কষে দেখি ১০ ক্লাস ১০|Koshe Dekhi 10 Class10
9. ABCD একটি বৃত্তস্থ চতুর্ভুজ । DE জ্যা ∠BDC – এর বহির্দিখন্ডক । প্রমাণ করি যে , AE ( বা বর্ধিত AE ) ∠BAC এর বহির্দ্বিখন্ডক ।
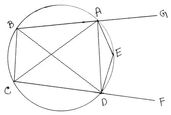
বৃত্তস্থ চতুর্ভুজ ABCD এর ∠BDC এর বহির্দ্বিখন্ডক DE জ্যা । প্রমাণ করতে হবে যে , AE , ∠BAC এর বহির্দ্বিখন্ডক ।
অঙ্কনঃ CD কে F পর্যন্ত এবং BA কে G পর্যন্ত বর্ধিত করা হল ।
প্রমাণঃ বৃত্তস্থ চতুর্ভুজ AEDB থেকে পাই ,
যেহেতু বৃত্তস্থ চতুর্ভুজের বহিঃস্থ কোন বিপরীত কোনের সমান
∴ ∠EAG = ∠EDB
আবার যেহেতু ED , ∠BAC এর বহির্দ্বিখন্ডক তাই ,
∠EDB = ∠EDF
∴ ∠EAG = ∠EDF —-(i)
আবার, বৃত্তস্থ চতুর্ভুজ ACDE থেকে পাই ,
∠EDF = ∠EAC [ ∵ বৃত্তস্থ চতুর্ভুজের বহিঃস্থ কোন বিপরীত অন্তঃস্থ কোনের সমান ]—(ii)
(i) ও (ii) নং সমীকরণ থেকে পাই ,
∠EAG = ∠EAC
∴ EA , ∠BAC এর বহির্দ্বিখন্ডক [প্রমাণিত ]।
10. ABC ত্রিভুজের AC ও AB বাহুর ওপর BE ও CF যথাক্রমে লম্ব । প্রমান করি যে , B ,C,E,F বিন্দু চারটি সমবৃত্তস্থ ।এর থেকে প্রমান করি যে , ∆ AEF ও ∆ ABC এর দুটি করে কোন সমান ।
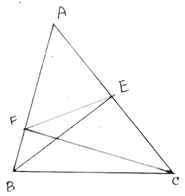
ABC এর AC এবং AB বাহুর ওপর যথাক্রমে BE ও CF লম্ব । প্রমান করতে হবে যে , B,C,E,F বিন্দু চারটি সমবৃত্তস্থ ।
অঙ্কনঃ E ,F যোগ করা হল ।
প্রমাণঃ ∠CEB = 1 সমকোণ
এবং ∠BFC = 1 সমকোণ
∴ একই রেখাংশ BC এর ওপর অবস্থিত দুটি কোন ∠CEB = ∠BFC = 1 সমকোন
∴ B ,C,E,F বিন্দু চারটি সমবৃত্তস্থ ( প্রমানিত)
∆AEF এবং ∆ABC থেকে পাই ,
যেহেতু B,C,E,F বিন্দু চারটি সমবৃত্তস্থ
∴ বৃত্তস্থ চতুর্ভুজ BCEF এর
বহিঃস্থ কোন ∠AEF = বিপরীত অন্তঃস্থ কোন ∠FBC
এবং বহিঃস্থ কোন ∠AFE = বিপরীত অন্তঃস্থ কোন ∠ECB
∆AEF এবং ∆ABC থেকে পাই ,
∠AEF=∠ABC [ ∵∠FBC =∠ABC]
∠AFE = ∠ACB [ ∵∠ECB = ∠ACB ]
∴ ∆AEF ও ∆ABC এর দুটি করে কোন সমান [প্রমাণিত ]।
মাধ্যমিক গণিত প্রকাশ বইএর সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
11. ABCD একটি সামান্তরিক । A ও B বিন্দুগামী একটি বৃত্ত AD ও BC কে যথাক্রমে E ও F বিন্দুতে ছেদ করে । প্রমান করি যে E ,F ,C ,D বিন্দু চারটি সমবৃত্তস্থ ।
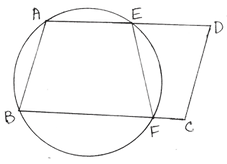
অঙ্কনঃ P,Q যুক্ত করা হল ।
প্রমাণঃ এখানে ABCD একটি সামান্তরিক ।
∴ ∠BAD +∠ADC = 2সমকোণ [ ∵সামান্তরিকের একই পার্শ্বস্থ অন্তঃকোণের সমষ্টি 2 সমকোণ] —– (i)
আবার , ABFE একটি বৃত্তস্থ চতুর্ভুজ ।
∴ ∠BAE +∠EFB = 2 সমকোণ [ ∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক ]
কিন্তু , ∠EFB+∠EFC = 2 সমকোণ [ ∵ EF , BC বাহুর ওপর দন্ডায়মান ]
∴ ∠BAE +∠EFB=∠EFB+∠EFC
∴ ∠EFC = ∠BAE
∴ ∠EFC=∠BAD
∴ ∠EFC +∠ADC = 2সমকোণ [(i) থেকে ]
∴ ∠EFC +∠PDC = 2 সমকোণ ।
∴ EFCD একটি বৃত্তস্থ চতুর্ভুজ
∴ E,F ,C,D বিন্দু চারটি সমবৃত্তস্থ ।[প্রমাণিত ]
বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য কষে দেখি ১০|কষে দেখি ১০ ক্লাস ১০|Koshe Dekhi 10 Class10
12. ABCD একটি বৃত্তস্থ চতুর্ভুজ , যার বর্ধিত AB এবং DC পরস্পরকে P বিন্দুতে এবং AD ও BC বাহুকে বর্ধিত করলে R বিন্দুতে মিলিত হয় । ∆BCP এবং ∆CDR এর পরিবৃত্তদ্বয় T বিন্দুতে ছেদ করে । প্রমান করি যে P ,T ,R সমরেখ ।
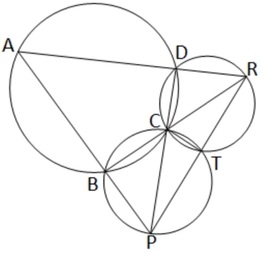
ABCD একটি বৃত্তস্থ চতুর্ভুজ , যার বর্ধিত AB এবং DC পরস্পরকে P বিন্দুতে এবং বর্ধিত AD ও BC পরস্পর R বিন্দুতে মিলিত হয়েছে । ∆BCP এবং ∆CDR এর পরিবৃত্তদ্বয় T বিন্দুতে ছেদ করেছে । প্রমান করতে হবে যে P,T,R সমরেখ ।
অঙ্কনঃ P,T ; R,T এবং C,T যুক্ত করা হল ।
প্রমাণঃ BCTP একটি বৃত্তস্থ চতুর্ভুজ ।
∴ ∠CTP +∠CBP = 180 [ ∵বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি সম্পূরক ]
বা , ∠CTP = 180-CBP = ∠ABC [ ∵ AB বাহুর ওপর BC দন্ডায়মান ]
এখন , ∠CTP +∠CTR = ∠ABC +∠CDA = 2 সমকোণ [ ∵ ABCD বৃত্তস্থ চতুর্ভুজ ]
যেহেতু , ∠CTP এবং ∠CTR এর CT সাধারন বাহু এবং কোন দুটির সমষ্টি 2 সমকোণ ,
∴ P ,T ,R সমরেখ ।[প্রমাণিত ]
13. ABC ত্রিভুজের লম্ববিন্দু O ; প্রমান করি যে O বিন্দুটি পাদত্রিভুজের অন্তঃকেন্দ্র ।
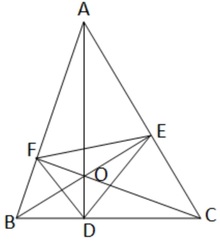
∆ABC এর শীর্ষবিন্দুত্রয় থেকে বিপরীত বাহুগুলির ওপর অঙ্কিত লম্বত্রয় AD ,BE ,CF তিনটি O বিন্দুতে ছেদ করেছে । প্রমান করতে হবে যে O বিন্দুটি পাদত্রিভুজ ∆DEF এর অন্তঃকেন্দ্র ।
অঙ্কন ঃ D,E ; E,F এবং F,D যুক্ত করা হল ।
প্রমাণঃ O , ABC এর লম্ববিন্দু । যেহেতু সুক্ষকোনী ত্রিভুজের শীর্ষ থেকে বিপরীত বাহুর ওপর অঙ্কিত লম্ব তার পাদত্রিভুজের কোনকে সমদ্বিখন্ডিত করে ,
∴ AD রেখা , ∠FDE কে, BE রেখা, ∠DEF কে এবং CF রেখা , ∠DFE কে সমদ্বিখন্ডিত করে ।
সুতরাং , ∠DEF এর অন্তর্দ্বিখন্ডকত্রয় O বিন্দুতে মিলিত হয়েছে ।
∴ O ,∠DEF এর অন্তঃকেন্দ্র [প্রমাণিত ]।
বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য কষে দেখি ১০|কষে দেখি ১০ ক্লাস ১০|Koshe Dekhi 10 Class10
14. ABCD এমন একটি বৃত্তস্থ চতুর্ভুজ এঁকেছি যে AC , ∠BAD কে সমদ্বিখন্ডিত করেছে । AD কে E পর্যন্ত বাড়ানো হল যাতে , DE =AB হয় । প্রমান করতে হবে যে , CE = CA
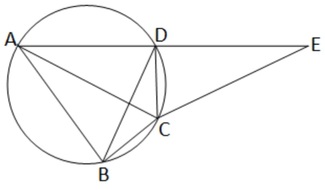
অঙ্কনঃ B,D যুক্ত করা হল ।
প্রমাণঃ ∠BAC = ∠BDC [ একই বৃত্তাংশস্থ সকল কোনের মান সমান ]
এবং ∠CAD = ∠DBC [ একই বৃত্তাংশস্থ সকল কোনের মান সমান ]
আবার , ∠BAC = ∠CAD [ ∵ AC , ∠BAD এর সমদ্বিখণ্ডক ]
∴ ∠BDC = ∠DBC
∴ ∆BCD থেকে পাই , CD =BC
যেহেতু AE সরলরেখার ওপর D বিন্দুতে DE দণ্ডায়মান
∴ ∠EDC + ∠ADC = 2সমকোণ
আবার , ∠ADC + ∠ABC = 2 সমকোন [ ∵ ABCD বৃত্তস্থ চতুর্ভুজ ]
∴ ∠EDC +∠ADC = ∠ADC+∠ABC
অর্থাৎ , ∠EDC = ∠ABC
এখন ∆DEC ও ∆ABC এর মধ্যে ,
DE = AB ( প্রদত্ত )
∠EDC = ∠ABC ( পূর্বে প্রমানিত )
CD = BC ( পূর্বে প্রমানিত )
∴ ∆DCE = ∆ABC [ S-S-S শর্তানুসারে ]
∴ CE = CA (অনুরূপ বাহু )[প্রমাণিত ]
বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য কষে দেখি ১০|কষে দেখি ১০ ক্লাস ১০|Koshe Dekhi 10 Class10
15.দুটি বৃত্তের একটি অপরটির কেন্দ্র O বিন্দুগামী এবং বৃত্তদুটি পরস্পরকে A ও B বিন্দুতে ছেদ করেছে । A বিন্দুগামী একটি সরলরেখা O বিন্দুগামী বৃত্তকে P বিন্দুতে এবং O কেন্দ্রীয় বৃত্তকে R বিন্দুতে ছেদ করেছে । P ,B ও R ,B যুক্ত করে প্রমান কর যে PR = PB।
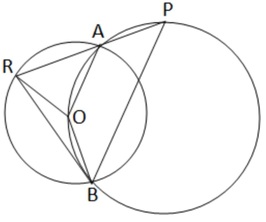
দুটি বৃত্তের একটি অপরটির কেন্দ্র O বিন্দুগামী এবং বৃত্ত দুটি পরস্পরকে A এবং B বিন্দুতে ছেদ করেছে । A বিন্দুগামী একটি সরলরেখা O বিন্দুগামী বৃত্তকে P বিন্দুতে এবং O কেন্দ্রীয় বৃত্তকে R বিন্দুতে ছেদ করেছে । P,B ও R ,B যুক্ত করা হল । প্রমান করতে হবে PR = PB
অঙ্কনঃ O,A ; O,R ; O,B যুক্ত করা হল ।
প্রমাণঃ ∆ROB এর RO = OB [ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠ORB = ∠OBR ——(i)
AOR এর OA = OR [ একই বৃত্তের ব্যাসার্ধ ]
∴ ∠ARO = ∠OAR
আবার চতুর্ভুজ AOBP সমবৃত্তস্থ ।
∴ ∠OBP+∠OAP = 2 সমকোণ
আবার PR বাহুর ওপর A বিন্দুতে AO দন্ডায়মান ।
∴ ∠OAP+∠OAR = 2 সমকোণ
∴ ∠OBP= ∠OAR
∴ ∠ARO = ∠OBP —– (ii)
এখন , ∠PRB = ∠ARO+∠ORB =∠OBP+∠OBR=∠PBR
∴ ∆PBR এর ∠PRB = ∠PBR
∴ PR = PB [প্রমাণিত ]
বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য কষে দেখি ১০|কষে দেখি ১০ ক্লাস ১০|Koshe Dekhi 10 Class10
মাধ্যমিক গণিত প্রকাশ বইএর সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
16. প্রমান করি যে একটি সুষম পঞ্চভুজের যে কোনো চারটি শীর্ষবিন্দু সমবৃত্তস্থ ।
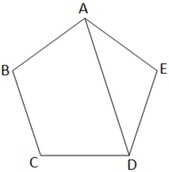
ABCDE একটি সুষম পঞ্চভুজ । প্রমান করতে হবে যে , এর চারটি বিন্দু সমবৃত্তস্থ ।
অঙ্কনঃ A ,D যুক্ত করা হল ।
প্রমাণঃ সুষম পঞ্চভুজের প্রতিটি কোনের মান {(2✕5-4)✕90º}/5 =540º/5=108º
এবং প্রতিটি বাহু সমান , অর্থাৎ ,
AB =BC=CD=DE=EA
এখন , ∆ADE এর DE =EA
∴ ∠EAD =∠EDA= (180º-108º)/2 = 36º
সুতরাং , ∠BAD = 108º-36º=72º
∴ ∠BCD+∠BAD = 108º+72º=180º
∴ ABCD চতুর্ভুজের বিপরীত কোনগুলির সমষ্টি 180º
∴ ABCD চতুর্ভুজটি সমবৃত্তস্থ ।
সুতরাং একটি পঞ্চভুজের যেকোনো চারটি বিন্দু সমবৃত্তস্থ [প্রমাণিত ]
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
17. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A)
(A) বহু বিকল্পীয় প্রশ্ন (M.C.Q):
(i) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস । ABCD বৃত্তস্থ চতুর্ভুজ । ADC = 120º হলে BAC এর মান
(a) 50º
(b) 60º
(c ) 30º
(d) 40º
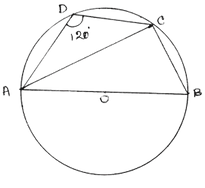
Ans: (c ) 30º
সমাধানঃ ABCD বৃত্তস্থ চতুর্ভুজ ।
∴ ∠ADC+∠ABC = 180º [∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক]
∴ ∠ABC = 180º-∠ADC
বা, ∠ABC = 180º-120º
বা , ∠ABC = 60º
আবার , ∠ACB = 90º [ ∵ অর্ধবৃত্তস্থ কোন সমকোন ]
এখন , ABC থেকে পাই ,
∠ABC+∠ACB+∠BAC = 180º
বা, 60º+90º+∠BAC = 180º
বা , ∠BAC = 30º
(ii) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস । ABCD বৃত্তস্থ চতুর্ভুজ ।∠ABC = 65º , ∠DAC = 40º হলে ∠BCD এর মান
(a) 75º
(b) 105º
(c ) 115º
(d) 80º
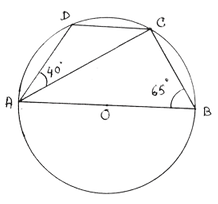
Ans: (c ) 115º
সমাধানঃ ABCD একটি বৃত্তস্থ চতুর্ভুজ ।
∴ ∠ABC+∠ADC = 180º [∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক ]
∴ ∠ADC
= 180º-ABC
= 180º-65º
= 115º
∠ADC=115º
∠ACD
= 180º-(ADC+DAC)
=180º-(115º+40º)
=180º-155º
=25º
∠ACD = 25º
∠ACB = 90º [ অর্ধবৃত্তস্থ কোন ]
∴ ∠BCD = ∠ACB+∠ACD = 90º+25º= 115º
∠BCD = 115º
(iii) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস । ABCD বৃত্তস্থ চতুর্ভুজ যার AB ∥ DC এবং ∠BAC = 25º হলে ∠DAC এর মান
(a) 50º
(b) 25º
(c ) 130º
(d) 40º
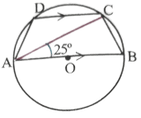
Ans: (d) 40º
∠BAC = ∠ACD [ একান্তর কোন ,AB ∥ DC , AC ভেদক ]
∴ ∠ACD = 25º
∠ACB = 90º [ অর্ধবৃত্তস্থ কোন সমকোন ]
∴ ∠ABC = 180º-(ACB+BAC)
বা, ∠ABC= 180º-(90º+25º)
বা , ∠ABC = 180º-115º
বা , ABC = 65º
∴ ∠ADC = 180º-65º = 115º [বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক ]
∴ ∠DAC
= 180º-(∠ADC+∠ACD)
=180º-(115º+25º)
=180º-140º
=40º
বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য কষে দেখি ১০|কষে দেখি ১০ ক্লাস ১০|Koshe Dekhi 10 Class10
(iv) পাশের চিত্রে ABCD একটি বৃত্তস্থ চতুর্ভুজ । BA কে F বিন্দু পর্যন্ত বর্ধিত করা হল । AE ∥ CD , ∠ABC = 92º এবং ∠FAE = 20º হলে , ∠BCD এর মান
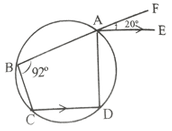
(a) 20º
(b) 88º
(c) 108º
(d) 72º
Ans: (c) 108º
সমাধানঃ ABCD বৃত্তস্থ চতুর্ভুজের ∠ABC = 92º
∴ ∠ADC = 180º-92º = 88º [ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক ]
∠ADC = ∠DAE [ একান্তর কোন , AE ∥ CD , AD ভেদক ]
∴ ∠DAE = 88º
∴ ∠DAF = 88º+20º = 108º
∴ ∠BCD = 108º [∵ বৃত্তস্থ চতুর্ভুজের বহিঃস্থ কোন,অন্তঃস্থ বিপরীত কোনের সমান ]
বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য কষে দেখি ১০|কষে দেখি ১০ ক্লাস ১০|Koshe Dekhi 10 Class10
(v) পাশের চিত্রে দুটি বৃত্ত পরস্পরকে C বিন্দুতে ছেদ করে । D ও C বিন্দুগামী দুটি সরলরেখা একটি বৃত্তকে যথাক্রমে A ও B বিন্দুতে এবং অপর বৃত্তকে E ও F বিন্দুতে ছেদ করে । ∠DAB =75º হলে ∠DEF এর মান
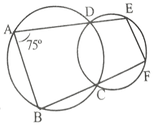
(a) 75º
(b) 70º
(c ) 60º
(d) 105º
Ans: (d) 105º
সমাধানঃ
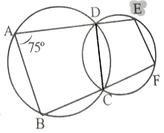
ABCD বৃত্তস্থ চতুর্ভুজ ।
এবং ∠BAC = 75º
∴ ∠BCD = 180º -75º =105º [∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক ]
∴ ∠DCF = 180º-105º=75º [ ∵ BF সরলরেখার ওপর C বিন্দুতে , CD দণ্ডায়মান ]
আবার , DCFE বৃত্তস্থ চতুর্ভুজ
∴ ∠DEF = 180º-75º =105º [∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক ]
বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য কষে দেখি ১০|কষে দেখি ১০ ক্লাস ১০|Koshe Dekhi 10 Class10
(B ) সত্য/ মিথা লিখিঃ
(i) একটি বৃত্তস্থ চতুর্ভুজের বিপরীত কোন পরস্পর পূরক ।
উত্তরঃ মিথ্যা ।
(ii) একটি বৃত্তস্থ চতুর্ভুজের একটি বাহুকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোন বিপরীত অন্তঃস্থ কোণের সমান হয় ।
উত্তরঃ সত্য ।
(C ) শূন্যস্থান পূরণ করিঃ
(i) একটি চতুর্ভুজের বিপরীত কোণদ্বয় পরস্পর সম্পূরক হলে চতুর্ভুজের শীর্ষবিন্দুগুলি__________ ।
উত্তরঃ সমবৃত্তস্থ ।
(ii) একটি বৃত্তস্থ সামান্তরিক একটি ___________ চিত্র ।
উত্তরঃ আয়তকার চিত্র ।
(iii) একটি বর্গাকার চিত্রের শীর্ষবিন্দুগুলি _______________ ।
উত্তরঃ সমবৃত্তস্থ ।
18. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.):
(i) পাশের চিত্রে P ও Q কেন্দ্রবিশিষ্ট বৃত্তদুটি B ও C বিন্দুতে ছেদ করেছে । ACD একটি সরলরেখাংশ । ∠ARB= 150º, ∠BQD = x হলে, x এর মান নির্ণয় করি ।
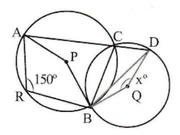
সমাধানঃ ∠ARB = 150º
ARBC বৃত্তস্থ চতুর্ভুজ এবং বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক।
∴ ∠ACB+∠ARB = 180º
বা, ∠ACB = 180-150=30º
আবার , ∠ACD = 180º
∴ ∠BCD = 180º–∠ACB
বা,∠BCD=180º-30º
বা,∠BCD=150º
প্রবিদ্ধ কোন ∠BQD = 2 ✕∠BCD [ ∵ একই বৃত্তচাপের ওপর অবস্থিত কেন্দ্রস্থ কোন পরিধিস্থ কোনের দ্বিগুন ]
∴ প্রবিদ্ধ ∠BQD = 2 ✕150º =300º
বা, ∠BQD =360º– প্রবিদ্ধ ∠BQD
বা, ∠BQD= 360º-300º
বা, ∠BQD=60º
∴ x = 60º [উত্তর]
(ii) পাশের চিত্রে দুটি বৃত্ত পরস্পর P ও Q বিন্দুতে ছেদ করে । ∠QAD=80º এবং ∠PDA=84º হলে, ∠QBC ও ∠BCP এর মান নির্ণয় কর ।
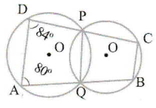
সমাধানঃ ∠QAD=80º
ADPQ বৃত্তস্থ চতুর্ভুজ ।
∴ ∠QAD+∠QPD=180º [ ∵ বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক ]
বা, ∠QPD=180º-∠QAD
বা,∠QPD=180º-80º
বা, ∠QPD=100º
আবার , DC একটি সরলরেখা
∴ ∠QPC=180º-100º=80º
আবার , PQBC বৃত্তস্থ চতুর্ভুজ
∴ ∠QPC+∠QBC = 180º [ যেহেতু , বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক]
বা, ∠QBC=180º-∠QPC
বা, ∠QBC=180º-80º
বা, ∠QBC=100º[উত্তর]
একিইভাবে ,∠PDA=84º হলে, বহিঃস্থ কোন ∠PQB=84º
∴ ∠PCB=180º-84º=96º [যেহেতু, ∠PQB এবং ∠PCB বৃত্তস্থ চতুর্ভুজের বিপরীত কোন অতএব তারা সম্পূরক]
∠PCB=96º[উত্তর]
বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য কষে দেখি ১০|কষে দেখি ১০ ক্লাস ১০|Koshe Dekhi 10 Class10
(iii) পাশের চিত্রে ∠BAD =60º , ∠ABC = 80º হলে , ∠DPC এবং ∠BQC এর মান নির্ণয় কর ।
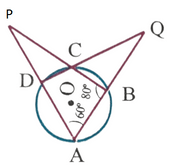
সমাধানঃ ABCD একটি বৃত্তস্থ চতুর্ভুজ ।
∠BAD =60º ( প্রদত্ত)
∴ ∠DCP=60º [ যেহেতু, বৃত্তস্থ চতুর্ভুজের কোনো একটি বহিঃস্থ কোনের মান অন্তঃস্থ বিপরীত কোণের সমান]
আবার, ∠ABC= 80º
∴ ∠CDP=80º [ যেহেতু, বৃত্তস্থ চতুর্ভুজের কোনো একটি বহিঃস্থ কোনের মান অন্তঃস্থ বিপরীত কোণের সমান]
∆ CPD ত্রিভুজ থেকে পাই,
∠CPD=180º-(∠CDP+∠DCP)
বা,∠CPD=180º-(80º+60º)
বা,∠CPD=180º-140º
বা,∠CPD=40º
∴ ∠DPC=40º [উত্তর]
আবার, ∠BCQ = ∠BAD=60º [ যেহেতু, বৃত্তস্থ চতুর্ভুজের কোনো একটি বহিঃস্থ কোনের মান অন্তঃস্থ বিপরীত কোণের সমান]
∠CBQ=180-∠ABC=180º-80º=100º
∆CQB থেকে পাই ,
∠BQC =180º-(∠BCQ+∠CBQ)
∴ ∠BQC=180º-(60º+100º)
বা,∠BQC =180º-160º
বা,∠BQC=20º
∴ ∠BQC=20º[উত্তর]
বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য কষে দেখি ১০|কষে দেখি ১০ ক্লাস ১০|Koshe Dekhi 10 Class10
(iv) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AC ব্যাস । ∠AOB=80º এবং ∠ACE=10º হলে , ∠BED-এর মান নির্ণয় কর ।
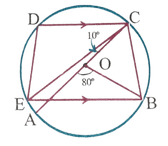
সমাধানঃ ∠AOB =80º
এখন,∠ACB=1/2 ✕∠AOB [ যেহেতু,AB বৃত্তচাপের ওপর ∠AOB কেন্দ্রস্থ কোন এবং ∠ACB পরিধিস্থ কোন]
∴ ∠ACB= 1/2✕ 80º=40º
আবার,∠ECB= ∠ACE+∠ACB
∴ ∠ECB=10º+40º
বা,∠ECB=50º
আবার , ∠BOC = 180º-∠AOB
বা,∠BOC=180º-80º
বা,∠BOC=100º
আবার , BC বৃত্তচাপের ওপর ∠BOC কেন্দ্রস্থ কোন এবং ∠BEC পরিধিস্থ কোন
∴ ∠BEC =1/2✕ ∠BOC [ যেহেতু কেন্দ্রস্থ কোন পরিধিস্থ কোণের দ্বিগুন ]
বা,∠BEC=1/2✕ 100º
বা, ∠BEC=50º
আবার, ∠BEC=∠DCE =50º [একান্তর কোন, কারণ EB ∥ DC এবং EC ভেদক ]
∴ ∠DCE=50º
∴ ∠DCB=∠DCE+∠ECB=50º+50º=100º
এখন,∠BED=180-∠DCB [ যেহেতু,DEBC একটি বৃত্তস্থ চতুর্ভুজ এবং বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক]
বা,∠BED=180º-100º
বা,∠BED=80º
∴∠BED=80º [উত্তর]
বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য কষে দেখি ১০|কষে দেখি ১০ ক্লাস ১০|Koshe Dekhi 10 Class10
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
(V) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB বৃত্তের ব্যাস । ∠AOD=140º এবং ∠CAB=50º হলে , ∠BED এর মান নির্ণয় করি।

সমাধানঃ ABDC একটি বৃত্তস্থ চতুর্ভুজ ।
∴ ∠CAB+∠BDC=180º
বা,50º+∠BDC=180º
বা,∠BDC=130º
∠BDE=180º-130º=50º [∵∠CDE=180º]
আবার, ∠BOD =180º-140º=40º
∆OBD ত্রিভুজের ক্ষেত্রে,
OB=OD [ একই বৃত্তের ব্যাসার্ধ]
∠OBD=∠ODB
∠OBD=(180º-∠BOD)/2
বা,∠OBD=(180º-40º)/2 [∵∠BOD=40º]
বা,∠ODB=70º
এখন, ∆BED ত্রিভুজের বহিঃস্থ কোন ∠OBD=∠BDE+∠BED (অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টি)
∴ 70º=50º+∠BED
বা,∠BED=70º-50º
∴ ∠BED=20º [উত্তর]
বৃত্তস্থ চতুর্ভুজ সংক্রান্ত উপপাদ্য কষে দেখি ১০|কষে দেখি ১০ ক্লাস ১০|Koshe Dekhi 10 Class10
Good work done here. I am very pleased to see the sums done. It will be better of students if they follow Anushilan as it saves your money from buying books.
Remarks -10/10
👍👍👍👍👍👍👍👍👍👍