রাশিবিজ্ঞান কষে দেখি 26.1|Koshe Dekhi 26.1 Class 10

রাশিবিজ্ঞান কষে দেখি 26.1|রাশিবিজ্ঞান কষে দেখি ২৬.১|মাধ্যামিক গণিত প্রকাশ দশম শ্রেণি (ক্লাস ১০)সমাধান| Ganit Prakash Somadhan Class 10 Statistics Koshe Dekhi 26.1|WBBSE Class 10 (Ten)(X) Math Solution Of Chapter 26|WB Board Class 10 Math Book Solution.

রাশিবিজ্ঞান কষে দেখি 26.1|Koshe Dekhi 26.1 Class 10

কষে দেখি – 26.1

1.আমি আমার 40  জন বন্ধুর বয়স নিচে ছকে লিখেছি ,

বয়স	15	16	17	18	19	20
বন্ধুর সংখ্যা	4	7	10	10	5	4

আমি আমার বন্ধুদের গড় বয়স প্রত্যক্ষ পদ্ধতিতে নির্ণয় করি ।

সমাধানঃ

বয়স (বছর) (xi )	বন্ধুর সংখ্যা (fi  )	xifi
15	4	60
16	7	112
17	10	170
18	10	180
19	5	95
20	4	80
মোট	∑ fi = 40	∑xifi = 697

∴ আমার বন্ধুর গড় বয়স =∑x_if_i / ∑ f_i =697/40= 17.425 =17.43 বছর (প্রায়)

2.গ্রামের 50 টি পরিবারের সদস্য সংখ্যা নীচের তালিকায় লিখেছি ।

সদস্য সংখ্যা	2	3	4	5	6	7
পরিবারের সংখ্যা	6	8	14	15	4	3

ওই 50 টি পরিবারের সদস্য সংখ্যা কল্পিত গড় পদ্ধতিতে লিখি ।

সমাধানঃ

ধরি কল্পিত গড় ( a ) = 4

সদস্য সংখ্যা ( xi)	পরিবারের সংখ্যা ( fi)	di = xi-a di = xi – 4	fidi
2	6	-2	-12
3	8	-1	-8
4 = a	14	0	0
5	15	1	15
6	4	2	8
7	3	3	9
মোট	∑ fi = 50		∑fidi=12

কল্পিত গড় পদ্ধতিতে গড় সদস্য সংখ্যা

= a + ( ∑f_id_i /  ∑ f_i )

= 4 + (12/50)

= 4 + 0.24

= 4.24 (উত্তর)

  3. যদি নীচের প্রদত্ত তথ্যের যৌগিক গড় 20.6 হয় , তবে a এর মান নির্ণয় করি ।

চল (xi)	10	15	a	25	35
পরিসংখ্যা	3	10	25	7	5

সমাধানঃ

প্রদত্ত তথ্যগুলির জন্য পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,

চল (xi)	পরিসংখ্যা (fi)	xifi
10	3	30
15	10	150
a	25	25a
25	7	175
35	5	175
মোট	∑ f i = 50	∑ xifi = 530+25a

যৌগিক গড় = ∑ x_if_i / ∑ f _i = (530+25a) / 50

আবার প্রস্নানুসারে যৌগিক গড় = 20.6

∴ a = 20

রাশিবিজ্ঞান কষে দেখি 26.1|Koshe Dekhi 26.1 Class 10

4. যদি নীচের প্রদত্ত  তথ্যের যৌগিক গড় 15 হয় , তবে p এর মান হিসাব করে লিখি ।

চল (xi)	5	10	15	20	25
পরিসংখ্যা (fi)	6	p	6	10	5

সমাধানঃ

প্রদত্ত তথ্য গুলির জন্য পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,

চল (xi)	পরিসংখ্যা (fi)	xifi
5	6	30
10	P	10p
15	6	90
20	10	200
25	5	125
মোট	∑ f i = 27+p	∑ xifi = 445+10p

যৌগিক গড় = ∑ x_if / ∑ f _i = (445+10p) / (27+p)

আবার প্রস্নানুসারে যৌগিক গড় = 15

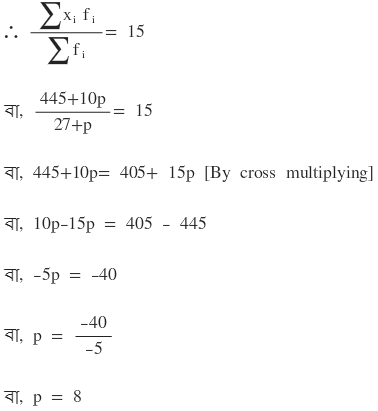
∴ p = 8

5. রহমত চাচা তার 50 টি বাক্সের বিভিন্ন সংখ্যায়ে আম ভরে পাইকারি বাজার এ নিয়ে যাবেন । কতগুলি বাক্সে কতগুলি আম রাখবেন তার তথ্য নীচের ছকে লিখে রাখলাম ।

আমের সংখ্যা	50-52	52-54	54-56	56-58	58-60
বাক্সের সংখ্যা	6	14	16	9	5

আমি ওই 50 টি বাক্সে গড় আমের সংখ্যা হিসাব করে লিখি (যে কোনও পদ্ধতিতে) ।

সমাধানঃ

প্রদত্ত তথ্যের জন্য পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,

আমের সংখ্যা	বাক্সের সংখ্যা (fi)	শ্রেণী মধ্যক (xi)	fixi
50-52	6	51	306
52-54	14	53	742
54-56	16	55	880
56-58	9	57	513
58-60	5	59	295
মোট	∑ fi = 50		∑ fixi = 2736

প্রত্যক্ষ পদ্ধতিতে গড় আম সংখ্যা

= ∑ f_ix_i / ∑ f_i  

= 2736/50

= 54.72

6. মহিদুল পাড়ার হাসপাতালের 100 জন রোগীর বয়স নীচের ছকে লিখে রাখল । ওই 100 জন রোগীর গড় বয়স হিসাব করে লিখি (যে কোনও পদ্ধতিতে) ।

বয়স (বছরে)	10-20	20-30	30-40	40-50	50-60	60-70
রোগীর সংখ্যা	12	6	22	20	18	20

সমাধানঃ

প্রদত্ত তথ্য গুলির জন্য পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,

বয়স (বছরে)	রোগীর সংখ্যা (fi)	শ্রেণী মধ্যক (xi)	fixi
10-20	12	15	180
20-30	8	25	200
30-40	22	35	770
40-50	20	45	900
50-60	18	55	990
60-70	20	65	1300
মোট	∑ fi = 100		∑ fixi = 4340

প্রত্যক্ষ পদ্ধতিতে রোগীর গড় বয়স

=∑ f_ix_i / ∑ f_i

= 4340 / 100

= 43.4 বছর ( উত্তর )

রাশিবিজ্ঞান কষে দেখি 26.1|Koshe Dekhi 26.1 Class 10

7. প্রত্যক্ষ পদ্ধতিতে নীচের তথ্যের গড় নির্ণয় করি ।

(i)

শ্রেণী সীমানা	0-10	10-20	20-30	30-40	40-50
পরিসংখ্যা	4	6	10	6	4

(ii)

শ্রেণী সীমানা	10-20	20-30	30-40	40-50	50-60	60-70
পরিসংখ্যা	10	16	20	30	13	11

সমাধানঃ

(i)  প্রদত্ত তথ্য গুলির জন্য পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,

শ্রেণী সীমানা	পরিসংখ্যা ( fi )	শ্রেণী মধ্যক (xi )	fixi
0-10	4	5	20
10-20	6	15	90
20-30	10	25	250
30-40	6	365	210
40-50	4	45	180
মোট	∑ fi = 30		∑ fixi = 750

প্রত্যক্ষ পদ্ধতিতে নির্ণেয় গড়

= ∑ f_ix_i / ∑ f_i

= 750 / 30

= 25 ( উত্তর )

(ii) প্রদত্ত তথ্য গুলির জন্য পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,

শ্রেণী সীমানা	পরিসংখ্যা (fi )	শ্রেণী মধ্যক (xi)	fixi
10-20	10	15	150
20-30	16	25	400
30-40	20	35	700
40-50	30	45	1350
50-60	13	55	715
60-70	11	65	715
মোট	∑ fi = 100		∑ fixi = 4030

প্রত্যক্ষ পদ্ধতিতে নির্ণেয় গড়

= ∑ f_ix_i / ∑ f_i

= 4030 / 100

= 40.3 (উত্তর )

রাশিবিজ্ঞান কষে দেখি 26.1|Koshe Dekhi 26.1 Class 10

8. কল্পিত গড় পদ্ধতিতে নীচের তথ্যের গড় নির্ণয় করি ।

(i)

শ্রেণী সীমানা	0-40	40-80	80-120	120-160	160-200
পরিসংখ্যা	12	20	25	20	13

(ii)

শ্রেণী সীমানা	25-35	35-45	45-55	55-65	65-75
পরিসংখ্যা	4	10	8	12	6

সমাধানঃ

প্রদত্ত তথ্য গুলির জন্য পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,

ধরি কল্পিত গড় = 100

শ্রেণী সীমানা	পরিসংখ্যা (fi)	শ্রেণী মধ্যক (xi)	di = xi – a di = xi -100	fidi
0-40	12	20	-80	-960
40-80	20	60	-40	-800
80-120	25	100 = a	0	0
120-160	20	140	40	800
160-200	13	180	80	1040
মোট	∑ f i = 90			∑ fidi = 80

কল্পিত গড় পদ্ধতিতে নির্ণেয় গড়

= a+ ( ∑ f_id_i / ∑ f _i )

= 100+ (80/90)

= 100 + 0.89

= 100.89 ( উত্তর )

রাশিবিজ্ঞান কষে দেখি 26.1|Koshe Dekhi 26.1 Class 10

(ii) সমাধানঃ

প্রদত্ত তথ্য গুলির জন্য পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,

ধরি কল্পিত গড় = 50

শ্রেণী সীমানা	পরিসংখ্যা (fi)	শ্রেণী মধ্যক (xi)	di = xi-a di = xi -50	fidi
25-35	4	30	-20	-80
35-45	10	40	-10	-100
45-55	8	50 = a	0	0
55-60	12	60	10	120
60-65	6	70	20	120
মোট	∑ f i =40			∑ fidi  = 60

কল্পিত গড় পদ্ধতিতে নির্ণেয় গড়

= a+ ( ∑ f_id_i / ∑ f _i )

=50 + (60/40)

= 50 + 1.5

= 51 .5 ( উত্তর )

রাশিবিজ্ঞান কষে দেখি 26.1|Koshe Dekhi 26.1 Class 10

9. ক্রমবিচ্যুতি পদ্ধতিতে নীচের তথ্যের গড় নির্ণয় করি ।

(i)

শ্রেণী – সীমানা	0-30	30-60	60-90	90-120	120-150
পরিসংখ্যা	12	15	20	25	8

(ii)

শ্রেণী – সীমানা	0-14	14-28	28-42	42-56	56-70
পরিসংখ্যা	7	21	35	11	16

সমাধানঃ

(i) প্রদত্ত তথ্য গুলির জন্য পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,

ধরি কল্পিত গড় = 75 এবং শ্রেণী দৈর্ঘ্য = 30

শ্রেণী সীমানা	পরিসংখ্যা (fi)	শ্রেণী মধ্যক (xi)	ui = (xi– a)/30	fiui
0-30	12	15	-2	-24
30-60	15	45	-1	-15
60-90	20	75 = a	0	0
90- 120	25	105	1	25
120 – 150	8	135	2	16
মোট	∑ fi = 80			∑ fiui =2

ক্রম- বিচ্যুতি পদ্ধতিতে নির্ণেয় গড়

= a + { h× ( ∑ f_iu_i / ∑ f_i ) }

= 75 + {30 × (2 / 80 )}

= 75 + 0.75

= 75.75 ( উত্তর )

রাশিবিজ্ঞান কষে দেখি 26.1|Koshe Dekhi 26.1 Class 10

(ii) সমাধানঃ

 প্রদত্ত তথ্য গুলির জন্য পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,

ধরি কল্পিত গড় = 35  এবং শ্রেণী দৈর্ঘ্য = 14

শ্রেণী সীমানা	পরিসংখ্যা (fi)	শ্রেণী মধ্যক (xi)	ui = (xi– a)/14	fiui
0-14	7	7	-2	-14
14-28	21	21	-1	-21
28-42	35	35 = a	0	0
42- 56	11	49	1	11
56-70	16	63	2	32
মোট	∑ fi =90			∑ fiui = 8

ক্রম- বিচ্যুতি পদ্ধতিতে নির্ণেয় গড়

= a + { h ✕ (∑ f_iu_i / ∑ f_i ) }

= 35 + {14 × (8 /90)}

= 35+ 1.24

=36.24 (উত্তর )

রাশিবিজ্ঞান কষে দেখি 26.1|Koshe Dekhi 26.1 Class 10

10. যদি নীচের পরিসংখ্যা বিভাজন্ তালিকার নম্বরের যৌগিক গড় 24 হয় , তবে p এর মান নির্ণয় করো ।

শ্রেণী সীমানা	0-10	10-20	20-30	30-40	40-50
ছাত্র সংখ্যা	15	20	35	p	10

সমাধানঃ

প্রদত্ত তথ্য গুলির জন্য পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,

শ্রেণী সীমানা (প্রাপ্ত নম্বর)	ছাত্র সংখ্যা (fi )	শ্রেণী মধ্যক (xi  )	fixi
0-10	15	5	75
10-20	20	15	300
20-30	35	25	875
30-40	P	35	35p
40-50	10	45	450
মোট	∑ fi =80+p		∑fixi =1700+35p

∴ যৌগিক গড় = (1700 + 35p)/(80+p)

প্রস্নানুসারে যৌগিক গড় = 24

রাশিবিজ্ঞান কষে দেখি 26.1|Koshe Dekhi 26.1 Class 10

11. আলচনা সভায় উপস্থিত ব্যাক্তিদের বয়স এর তালিকা দেখি এবং গড় বয়স নির্ণয় করি ।

সমাধানঃ

বয়স (বছর)	30-34	35-39	40-44	45-49	50-54	55-59
রোগীর সংখ্যা	10	12	15	6	4	3

সমাধানঃ

বয়স (বছর )	শ্রেণী সীমানা	রোগী সংখ্যা ( fi )	শ্রেণী মধ্যক (xi )	ui = (xi-a) / 5	fi ui
30-34	29.5-34.5	10	32	-2	-20
35-39	34.5-39.5	10	37	-1	-12
40-44	39.5-44.5	15	42=a	0	0
45-49	44.5-49.5	6	47	1	6
50-54	49.5-54.5	4	52	2	8
55-59	54.5-59.5	3	57	3	9
মোট		∑ fi = 50			∑fiui = – 9

এক্ষেত্রে কল্পিত গড় (a) = 42 এবং শ্রেণী দৈর্ঘ্য (h) = 5

∴ আলোচনা সভায় উপস্থিত ব্যাক্তিদের বয়সের গড়

= a + { h ✕ (∑ f_iu_i / ∑ f_i ) }

 = 42+ {5 × (-9/50)}

= 42 – 0.9

= 41.1 বছর ( উত্তর )

রাশিবিজ্ঞান কষে দেখি 26.1|Koshe Dekhi 26.1 Class 10

12.নীচের তথ্যের গড় নির্ণয় করি ।

শ্রেণী সীমানা	5-14	15-24	25-34	35-44	45-54	55-64
পরিসংখ্যা	3	6	18	20	10	3

সমাধানঃ

শ্রেণী- সীমা	শ্রেণী সীমানা	পরিসংখ্যা (fi  )	শ্রেণী মধ্যক (xi )	ui= (xi-a)/10	fiui
5-14	4.5-14.5	3	9.5	-2	-6
15-24	14.5-24.5	6	19.5	-1	-6
25-34	24.5-34.5	18	29.5 = a	0	0
35-44	34.5-44.5	20	39.5	1	20
45-54	44.5-54.5	10	49.5	2	20
55-64	54.5-64.5	3	59.5	3	9
মোট		∑ fi = 60			∑fiui = 37

এক্ষেত্রে কল্পিত গড় (a ) = 29.5 এবং শ্রেণী দৈর্ঘ্য (h) = 10

ক্রম – বিচ্যুতি পদ্ধতিতে নির্ণেয় গড়

= a + { h ✕ (∑ f_iu_i / ∑ f_i ) }

= 29.5 + { 10 × (37/60) }

= 29.5 + (37/6)

= 29.5+ 6.17

= 35.67 (প্রায় ) (উত্তর )

রাশিবিজ্ঞান কষে দেখি 26.1|Koshe Dekhi 26.1 Class 10

13.ছাত্রীদের প্রাপ্ত নম্বরের গড় নির্ণয় করি যদি তাদের প্রাপ্ত নম্বরের ক্রমযৌগিক পরিসংখ্যা নিম্নরূপ হয়ঃ

শ্রেণী সীমা	10 এর কম	20 এর কম	30 এর কম	40 এর কম	50 এর কম
ছাত্রী সংখ্যা	5	9	17	29	45

সমাধানঃ

10 এর কম 5জন

∴ 0 থেকে 10 এর মধ্যে ছাত্রী সংখ্যা = 5 জন ।

20 এর কম 9 জন ।

∴ 10 থেকে 20 এর মধ্যে  ছাত্রী সংখ্যা = 9-5 = 4 জন

30 এর কম 17 জন ।

∴ 20 থেকে 30 এর মধ্যে ছাত্রী সংখ্যা = 17-9 = 8 জন ।

এইভাবে গণনা করলে পরিসংখ্যা  তালিকাটি হবে ,

শ্রেণী সীমানা	0-10	10-20	20-30	30-40	40-50
ছাত্রী সংখ্যা	5	4	8	12	16

উপরের তথ্যের জন্য পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,

শ্রেণী সীমানা	পরিসংখ্যা (fi)	শ্রেণী মধ্যক (xi)	ui =  (xi-a)/10	fi ui
0-10	5	5	-2	-10
10-20	4	15	-1	-4
20-30	8	25	0	0
30-40	12	35	1	12
40-50	16	45	2	32
মোট	∑ fi = 45			∑fidi = 30

এক্ষেত্রে a = 25 এবং h = 10

ছাত্রীদের প্রাপ্ত নম্বরের গড়

= a + { h ✕ (∑ f_id_i / ∑ f_i ) }

 = 25 + {10 × (30/45)}

= 25 + 6.67

= 31.67 (প্রায় ) [ উত্তর ]

রাশিবিজ্ঞান কষে দেখি 26.1|Koshe Dekhi 26.1 Class 10

14. নীচের তালিকার 64 জন ছাত্রের প্রাপ্ত নম্বরের গড় নির্ণয় করি ।

শ্রেণী সীমা (নম্বর)	1-4	4-9	9-16	16-17
ছাত্র সংখ্যা	6	12	26	20

সমাধানঃ

উপরের তথ্য গুলির জন্য পরিসংখ্যা বিভাজন তালিকা তৈরি করি ,

শ্রেণী সীমানা	পরিসংখ্যা (fi)	শ্রেণী মধ্যক (xi)	fixi
1-4	6	2.5	15
4-9	12	6.5	78
9-16	26	12.5	325
16-17	20	16.5	330
	∑ fi = 64		∑fixi = 748

প্রত্যক্ষ পদ্ধতিতে ছাত্র দের প্রাপ্ত নম্বরের গড়

= ∑f_ix_i / ∑ f_i

= 748/64

 = 11.69 (প্রায় ) [ উত্তর ]

আরও দেখুনঃ

• মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধান

• গণিত প্রকাশ বই-এর সব অধ্যায়ের সমাধান

• মাধ্যমিকের সকল বিষয়ের মক টেস্ট

• WBBSE Official Site

ধন্যবাদ । এই POST টি ভালো লাগলে SHARE করার অনুরোধ রইল । এইরকম আরও সুন্দর সুন্দর POST পেতে , আমাদের FACEBOOK PAGE টি LIKE করুন।