
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২ ক্লাস ১০ সমাধান|গণিত প্রকাশ দশম শ্রেণি (ক্লাস ১০)| WBBSE Madhyamik Ganit Prakash Class 10(Ten) (X) Math Solution Of Chapter 22|WB Board Class 10 Math Solution Of Chapter 22.
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২|কষে দেখি 22 ক্লাস 10
1. যদি কোনো ত্রিভুজের বাহুর দৈর্ঘ্য নিম্নরূপ হয় , তবে কোন ক্ষেত্রে ত্রিভুজটি সমকোণী ত্রিভুজ হবে হিসাব করে লিখিঃ
(i) 8 সেমি.,15 সেমি. , 17 সেমি.
(ii) 9 সেমি. , 11 সেমি., 6 সেমি.
(i) সমাধানঃ এক্ষেত্রে (8)2+(15)2 =(17)2 অর্থাৎ , অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল ,অপর বাহুগুলির উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলের সমান । সুতরাং ত্রিভুজটি নিশ্চিত ভাবে একটি সমকোণী ত্রিভুজ ।
(ii) সমাধানঃ এক্ষেত্রে (11)2 ≠ (9)2+(6)2 অর্থাৎ , অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল ,অপর বাহুগুলির উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলের সমষ্টির সমান নয় ।সুতরাং 9 সেমি. ,11সেমি. এবং 6 সেমি. বাহু বিশিষ্ট ত্রিভুজটি সমকোণী ত্রিভুজ হবে না ।
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২
2. আমাদের পাড়ার রাস্তায় একটি 15 মিটার লম্বা মই এমনভাবে রাখা আছে যে মইটি ভূমি থেকে 9 মিটার উঁচুতে অবস্থিত মিলিদের জানালা স্পর্শ করেছে । এবার ওই রাস্তার একই বিন্দুতে মইটির পাদদেশ রেখে মইটিকে ঘুরিয়ে এমনভাবে রাখা হল যে মইটি রাস্তার অপর প্রান্তে অবস্থিত আমাদের জানালা স্পর্শ করল । আমাদের ওই জানালা যদি ভূমি থেকে 12 মিটার উপরে থাকে ,তবে পাড়ার ওই রাস্তাটি কত চওড়া হিসাব করে লিখি ।
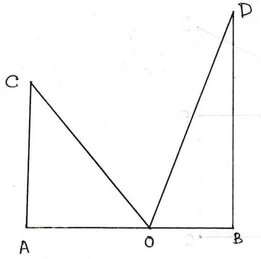
সমাধানঃ ধরাযাক , AB হল রাস্তাটির প্রস্থ ,O হল মইয়ের পাদদেশ , C ও D হল যথাক্রমে মিলিদের এবং আমাদের জানালার অবস্থান ।
∴ AC=9 মিটার , BD=12 মিটার এবং মইয়ের দৈর্ঘ্য OC = OD = 15 মিটার ।
এখন , ∆OAC এবং ∆OBD উভয়ই সমকোণী ত্রিভুজ ।
∴ ∆OAC সমকোণী ত্রিভুজে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই ,
OC2=OA2+AC2
বা, (15)2= OA2+(9)2
বা, OA2 = (15)2-(9)2
বা, OA2 = 225-81
বা, OA2 = 144
বা, OA2 = (12)2
বা, OA = 12
একই ভাবে ∆OBD সমকোণী ত্রিভুজে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই ,
OD2=OB2+BD2
বা, (15)2 = OB2+(12)2
বা, 225=OB2+144
বা, OB2 = 225-144
বা, OB2 = 81
বা, OB2 =(9)2
বা, OB = 9
∴ AB=AO+OB = (12+9)মিটার = 21 মিটার ।
∴ রাস্তাটি 21 মিটার চওড়া ।
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২
3. 10 সেমি. বাহু বিশিষ্ট কোনো রম্বসের একটি কর্ণের দৈর্ঘ্য 12 সেমি. হলে , রম্বসটির অপর কর্ণের দৈর্ঘ্য হিসাব করে লিখি ।
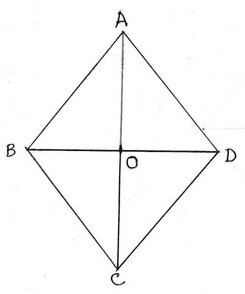
সমাধানঃ ধরি ,ABCD একটি রম্বস যার দুটি কর্ণ AC এবং BD পরস্পরকে O বিন্দুতে ছেদ করেছে এবং BD = 12 সেমি.।
যেহেতু রম্বসের প্রতিটি বাহুর দৈর্ঘ্য 10 সেমি. ∴ AB=BC=CD=DA=10 সেমি.।
যেহেতু,রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখন্ডিত করে
∴ OD = 6সেমি. এবং ∠AOD =90°
এখন , ∆AOD সমকোণী ত্রিভুজ থেকে পাই ,
AD2=OA2+OD2
বা, (10)2 = OA2 + (6)2
বা, 100 = (OA)2+36
বা, (OA)2 = 100-36
বা, OA2 = 64
বা, OA2 =(8)2
বা, OA =8
∴ AC = (2 ✕ 8)সেমি. = 16 সেমি.
∴ অপর কর্ণের দৈর্ঘ্য 16 সেমি. ।
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২
4. একটি ত্রিভুজ ∆PQR অঙ্কন করেছি যার ∠Q সমকোণ । QR বাহুর উপর S যে-কোনো একটি বিন্দু হলে , প্রমাণ করি যে , PS2+QR2 = PR2+QS2
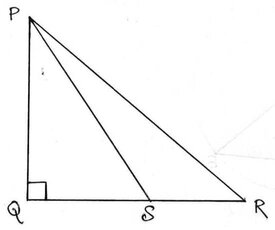
ধরি ,∆PQR একটি ত্রিভুজ যার Q সমকোণ । QR বাহুর উপর S যেকোনো একটি বিন্দু হলে , প্রমান করতে হবে যে , PS2+QR2=PR2+QS2
প্রমাণঃ যেহেতু , ∠Q সমকোণ , ∴ ∠PQS=∠PQR=90º
∴ ∆PQS এবং ∆PQR উভয়ই সমকোণী ত্রিভুজ ।
∆PQS সমকোণী ত্রিভুজ থেকে পাই ,
PS2 = PQ2+QS2 —-(i)
আবার ∆PQR সমকোণী ত্রিভুজ থেকে পাই,
PR2 = PQ2+QR2
বা, QR2 = PR2-PQ2 —-(ii)
(i) নং ও (ii) নং সমীকরণ যোগ করে পাই ,
∴ PS2 + QR2 = PQ2+QS2 +PR2-PQ2
বা, PS2 + QR2 = PR2 +QS2 [প্রমাণিত]
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২
5.প্রমাণ করি, যে –কোনো রম্বসের বাহুগুলির উপর অঙ্কিত বর্গের সমষ্টি কর্ণ দুটির উপর অঙ্কিত বর্গ দুটির সমষ্টির সমান ।
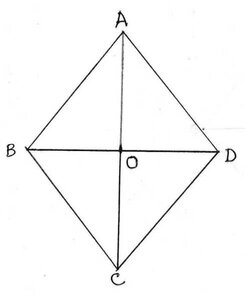
ধরি , ABCD একটি রম্বস,যার কর্ণদ্বয় হল AC এবং BD। প্রমান করতে হবে যে, AB2+BC2+CD2+DA2=AC2+BD2
প্রমাণঃ যেহেতু ABCD একটি রম্বস, ∴ AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে সমকোণে সমদ্বিখন্ডিত করে ।
∴OA=OC এবং OB=OD আবার OA =AC/2 এবং OB= BD/2
∴ ∆AOB সমকোণী ত্রিভুজ থেকে পাই AB2=OB2+OA2
∆BOC সমকোণী ত্রিভুজ থেকে পাই BC2=OB2+OC2
∆COD সমকোণী ত্রিভুজ থেকে পাই CD2=OC2+OD2
∆AOD সমকোণী ত্রিভুজ থেকে পাই DA2 = OA2+OD2
∴ AB2+BC2+CD2+DA2
= OB2+OA2+ OB2+OC2 +OC2+OD2+ OA2+OD2
= 2OA2+2OB2+2OC2+2OD2
= 4OA2+4OB2 [যেহেতু ,OA=OC এবং OB=OD]
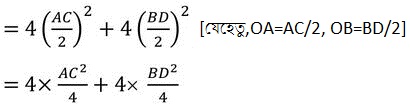
= AC2+BD2
∴ AB2+BC2+CD2+DA2 = AC2+BD2 [প্রমাণিত]
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
6. ABC একটি সমবাহু ত্রিভুজ । AD , BC বাহুর উপর লম্ব হলে, প্রমান করি যে , AB2+BC2+CA2=4AD2
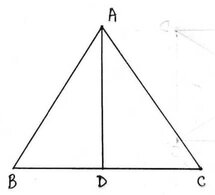
ধরি , ABC একটি সমবাহু ত্রিভুজ । A বিন্দু থেকে BC বাহুর উপরে AD লম্ব টানা হল , প্রমাণ করতে হবে যে , AB2+BC2+CA2=4AD2
প্রমাণঃ ABC একটি সমবাহু ত্রিভুজ এবং A বিন্দু থেকে BC বাহুর উপর AD লম্ব ∴ AD একটি মধ্যমা , সুতরাং D ,BC এর মধ্যবিন্দু ।
যেহেতু AD , BC বাহুর উপর লম্ব সুতরাং ∆ADB এবং ∆ADC উভয়ই সমকোণী ত্রিভুজ ।
∴ AB2= AD2+BD2
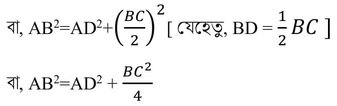
বা, 4AB2 = 4AD2+BC2
বা, 4AB2-BC2=4AD2
বা, 4AB2-AB2=4AD2 [ যেহেতু, AB=BC=CA]
বা, 3AB2= 4AD2
বা, AB2+AB2+AB2=4AD2
বা, AB2+BC2+CA2 = 4AD2 [যেহেতু, AB=BC=CA]
∴ AB2+BC2+CA2 = 4AD2 [প্রমাণিত]
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
7. একটি সমকোণী ত্রিভুজ ∆ABC অঙ্কন করলাম যার A সমকোণ । AB ও AC বাহুর উপর দুটি বিন্দু যথাক্রমে P ও Q নিলাম । P,Q; B,Q ও C,P যুক্ত করে ,প্রমাণ করি যে , BQ2+PC2=BC2+PQ2
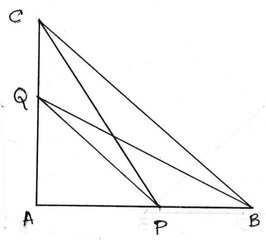
ধরি , ∆ABC একটি সমকোণী ত্রিভুজ যার A সমকোণ , AB ও AC বাহুর উপর দুটি বিন্দু যথাক্রমে P ও Q নেওয়া হল । P,Q;B,Q ও C,P যুক্ত করে ,প্রমাণ করতে হবে যে , BQ2+PC2=BC2+PQ2
প্রমাণঃ যেহেতু A সমকোণ
∴ ∆ABQ,∆APC, ∆APQ এবং ∆ABC প্রত্যেকে সমকোণী ত্রিভুজ ।
∆ABQ সমকোণী ত্রিভুজ থেকে পাই BQ2 = AQ2+AB2 —(i)
∆APC সমকোণী ত্রিভুজ থেকে পাই PC2 = AC2+AP2 —(ii)
∆APQ সমকোণী ত্রিভুজ থেকে পাই PQ2 = AP2+AQ2 —(iii)
∆ABC সমকোণী ত্রিভুজ থেকে পাই BC2 = AC2+AB2 —(iv)
(i) নং ও (ii) নং সমীকরণ যোগ করে পাই,
BQ2+PC2
= AQ2+AB2+AC2+AP2
= (AQ2+AP2 )+(AC2+AB2 )
= PQ2+BC2 [(iii) ও (iv) নং সমীকরণ থেকে পাই]
∴ BQ2+PC2 = PQ2+BC2 [প্রমাণিত ]
8. ABCD চতুর্ভুজের দুটি কর্ণ পরস্পরকে লম্বভাবে ছেদ করলে ,প্রমাণ করি যে , AB2+CD2=BC2+DA2
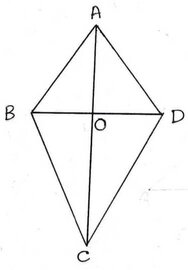
ধরি ,ABCD চতুর্ভুজের কর্ণদ্বয় AC ও BD পরস্পরকে O বিন্দুতে লম্বভাবে ছেদ করেছে । প্রমাণ করতে হবে যে , AB2+CD2=BC2+DA2
প্রমাণঃ যেহেতু ,ABCD চতুর্ভুজের কর্ণদ্বয় পরস্পরকে O বিন্দুতে লম্বভাবে ছেদ করেছে , ∴ ∆AOB,∆BOC,∆COA এবং ∆AOD প্রত্যেকে সমকোণী ত্রিভুজ ।
∆AOB সমকোণী ত্রিভুজ থেকে পাই AB2 = OA2+OB2 —(i)
∆BOC সমকোণী ত্রিভুজ থেকে পাই BC2 = OB2+OC2 —(ii)
∆COD সমকোণী ত্রিভুজ থেকে পাই CD2 = OC2+OD2 —(iii)
∆DOA সমকোণী ত্রিভুজ থেকে পাই AD2 = OA2+OD2 —(iv)
(i) ও (iii) নং সমীকরণ যোগ করে পাই ,
AB2+CD2
=OA2+OB2 +OC2+OD2
= (OA2+OD2)+(OB2+OC2)
= AD2+BC2 [ (ii)ও(iv) নং সমীকরণ থেকে পাই ]
∴ AB2+CD2 =AD2+BC2 [প্রমাণিত ]
9.একটি ত্রিভুজ ABC অঙ্কন করেছি যার উচ্চতা AD; AB>AC হলে প্রমাণ করি যে AB2-AC2=BD2-CD2
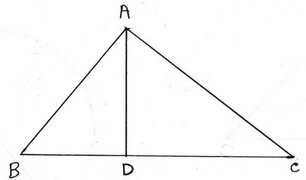
ধরি ,ABC একটি সমকোণী ত্রিভুজ যার ∠A সমকোণ , AD হল ত্রিভুজটির উচ্চতা এবং AB>AC , প্রমাণ করতে হবে যে ,AB2-AC2=BD2-CD2
প্রমাণঃ ABC সমকোণী ত্রিভুজে AD উচ্চতা ।
∴ AD⊥BC
∴ ∆ABD এবং ∆ACD উভয়ই সমকোণী ত্রিভুজ ।
∆ABD সমকোণী ত্রিভুজ থেকে পাই AB2 = AD2+BD2 —(i)
এবং ∆ACD সমকোণী ত্রিভুজ থেকে পাই AC2= AD2+CD2 —(ii)
(i) ও (ii) নং সমীকরণ বিয়োগ করে পাই ,
AB2-AC2
= (AD2+BD2)-(AD2+CD2)
= AD2+BD2-AD2-CD2
= BD2-CD2
∴ AB2-AC2 = BD2-CD2 [ প্রমাণিত ]
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২
10. ABC এর শীর্ষবিন্দু B ও C থেকে AC ও AB (AC > AB) বাহু দুটির উপর দুটি লম্ব অঙ্কন করেছি যারা পরস্পরকে P বিন্দুতে ছেদ করেছে । প্রমাণ করি যে , AC2+BP2=AB2+CP2
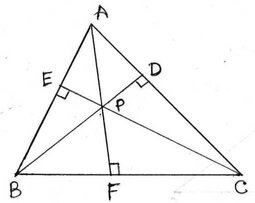
ABC একটি ত্রিভুজ যার B ও C বিন্দু থেকে AC ও BC বাহুর উপর দুটি লম্ব যথাক্রমে , BD ও CE অঙ্কন করেছি যারা পরস্পরকে P বিন্দুতে ছেদ করেছে । প্রমাণ করতে হবে যে , AC2+BP2=AB2+CP2
অঙ্কনঃ A,P যুক্ত করে বর্ধিত করা হল যা BC বাহুকে F বিন্দুতে ছেদ করেছে ।
প্রমাণঃ ∆ABC এর AF ⊥ BC[ যেহেতু , P লম্ববিন্দু]
সমকোণী ত্রিভুজ ∆ACF থেকে পাই AC2=AF2+CF2 —(i)
সমকোণী ত্রিভুজ ∆BPF থেকে পাই BP2=BF2+PF2 —(ii)
সমকোণী ত্রিভুজ ∆ABF থেকে পাই AB2=AF2+BF2 —(iii)
সমকোণী ত্রিভুজ ∆CPF থেকে পাই CP2=PF2+CF2 —(iv)
(i) ও (ii)নং সমীকরণ যোগ করে পাই ,
AC2 + BP2=BF2+PF2 +AF2+CF2
বা, AC2 + BP2 = AF2+BF2+PF2+CF2
বা, AC2 + BP2 = AB2+CP2 [(iii) নং ও(iv) নং সমীকরণ থেকে পাই ]
∴ AC2 + BP2 = AB2+CP2 [প্রমাণিত ]
11. ∆ABC একটি সমদ্বিবাহু ত্রিভুজ যার C সমকোণ । D ,AB এর উপর যে-কোনো একটি বিন্দু হলে , প্রমাণ কর যে, AD2+DB2=2CD2
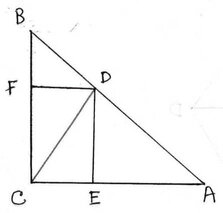
ধরাযাক ,∆ABC একটি সমকোণী সমদ্বিবাহু ত্রিভুজ যার কোণ ∠C সমকোণ । D, AB বাহুর উপর যেকোনো একটি বিন্দু , প্রমাণ করতে হবে যে , AD2+DB2= 2CD2
অঙ্কনঃ D বিন্দু থেকে AC এবং BC এর উপর DE এবং DF লম্ব অঙ্কন করা হল ।
প্রমাণঃ ∆ABC সমকোণী সমদ্বিবাহু ত্রিভুজ যার ∠C সমকোণ এবং AC = BC
∴ ∠CBA =∠CBA = 45°
আবার , ∆ADE এর ∠AED = 90° [যেহেতু , DE ⊥ AC] এবং ∠EAD = 45° , ∴ ∠ADE = 45°
∴ ∆ADE এর ∠ADE=∠EAD
∴ AE =DE
∆ADE ত্রিভুজে পিথাগোরাসের উপপাদ্য থেকে পাই ,
AD2 = AE2 + DE2
= DE2+DE2
= 2DE2 —(i)
আবার , ∆DBF এর ∠BFD = 90° এবং ∠FBD = 45°, ∴ ∠BDF = 45°
∴ ∆DBF এর ∠FBD=∠BDF , ∴ BF=FD
∆DBF সমকোণী ত্রিভুজে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই ,
BD2= BF2+FD2
= FD2+FD2
= 2FD2 —(ii)
(i) ও(ii) নং সমীকরণ যোগ করে পাই ,
AD2 +BD2
= 2DE2 + 2FD2
=2(DE2+FD2)
= 2(CF2+FD2) [ যেহেতু,CEDF চতুর্ভুজের ∠EDF,∠DEC এবং ∠DFC প্রত্যেকে 90°,∴CEDF একটি আয়তক্ষেত্র , ∴DE=CF এবং FD=CE]
= 2 CD2 [যেহেতু,∆CFD সমকোণী ত্রিভুজের ক্ষেত্রে CF2+FD2=CD2]
∴ AD2 +BD2 =2CD2 [ প্রমাণিত ]
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২
12. ABC ত্রিভুজে ∠A সমকোণ । CD মধ্যমা হলে, প্রমাণ করি যে , BC2 = CD2+3AD2
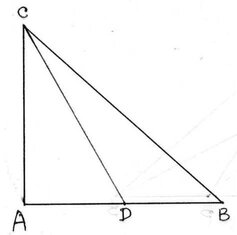
ধরাযাক ,ABC সমকোণী ত্রিভুজ যার A সমকোণ । CD মধ্যমা ,প্রমাণ করতে হবে যে , BC2 = CD2+3AD2
প্রমাণঃ ∆ABC এবং ∆CAD উভয়ই সমকোণী ত্রিভুজ যার A সমকোণ ।
∆ABC সমকোণী ত্রিভুজ থেকে পাই AB2+AC2 = BC2 —(i)
∆ACD সমকোণী ত্রিভুজ থেকে পাই CD2 = AD2+AC2—(ii)
∴ BC2 = AB2+AC2
এখন D, AC এর মধ্যবিন্দু ।
∴ AC=2AD—(iii)
∴ BC2 = (2AD)2 + (CD2-AD2) [(ii) ও (iii) নং সমীকরণ থেকে পাই ]
বা, BC2 = 4AD2+CD2-AD2
বা, BC2 = CD2 +3AD2 [প্রমাণিত ]
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
13. ABC ত্রিভুজের অভ্যন্তরস্থ একটি বিন্দু O থেকে BC , CA ও AB বাহুর উপর যথাক্রমে OX,OY ও OZ লম্ব অঙ্কন করেছি । প্রমাণ করি যে , AZ2+BX2+CY2 = AY2+CX2+BZ2
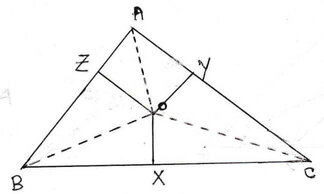
ABC একটি ত্রিভুজ যার অভ্যন্তরে O একটি বিন্দু এবং O বিন্দু থেকে BC,CA এবং AB বাহুর উপরে যথাক্রমে OX,OY এবং OZ লম্ব অঙ্কন করা হল ।
প্রমাণ করতে হবে যে , AZ2+BX2+CY2 = AY2+CX2+BZ2
অঙ্কনঃ O,A; O,B এবং O,C যুক্ত করা হল ।
প্রমাণঃ যেহেতু , OX,OY এবং OZ যথাক্রমে BC ,CA এবং AB বাহুর উপর লম্ব ।
∴ ∆AOZ,∆BOX ,∆COY , ∆AOY,∆COX এবং ∆BOZ প্রত্যেকে সমকোণী ত্রিভুজ ।
∆AOZ সমকোণী ত্রিভুজ থেকে পাই ,
OA2 = AZ2+OZ2
বা, AZ2 = OA2 – OZ2 —(i)
∆BOX সমকোণী ত্রিভুজ থেকে পাই ,
OB2 = OX2 +BX2
বা, BX2 = OB2 –OX2 —(ii)
∆COY সমকোণী ত্রিভুজ থেকে পাই ,
OC2 = OY2+CY2
বা, CY2 = OC2 – OY2 —(iii)
∆AOY সমকোণী ত্রিভুজ থেকে পাই ,
OA2 =OY2+AY2
বা, OA2 –OY2 = AY2—(iv)
∆COX সমকোণী ত্রিভুজ থেকে পাই ,
OC2 = OX2+CX2
বা, CX2 = OC2-OX2 —(v)
∆BOZ সমকোণী ত্রিভুজ থেকে পাই ,
OB2 = OZ2+BZ2
বা, BZ2 = OB2 –OZ2 —(vi)
∴ AZ2+BX2+CY2 = OA2 – OZ2 + OB2 –OX2 +OC2 – OY2
বা, AZ2+BX2+CY2 = OA2-OY2 + OC2-OX2 +OB2-OZ2
বা, AZ2+BX2+CY2 = AY2 +CX2+BZ2 [ (iv),(v) এবং (vi) নং সমীকরণ থেকে পাই ]
∴ AZ2+BX2+CY2 = AY2 +CX2+BZ2 [প্রমাণিত]
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২
14. ∆RST ত্রিভুজের ∠S সমকোণ । RS ও ST বাহুদ্বয়ের মধ্যবিন্দু যথাক্রমে X ও Y ; প্রমাণ করি যে , RY2+XT2 =5XY2
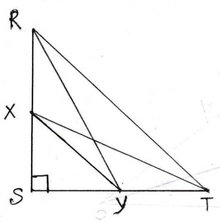
∆RST ত্রিভুজের S সমকোণ । RS ও ST বাহুদ্বয়ের মধ্যবিন্দু যথাক্রমে X ও Y ;প্রমাণ করতে হবে যে , RY2+XT2 =5XY2
প্রমাণঃ ∆RST ত্রিভুজে ∠S সমকোণ ।
∴ ∆RST , ∆RSY, ∆XST , ∆XSY প্রত্যেকে সমকোণী ত্রিভুজ ।
∴ সমকোণী ত্রিভুজ ∆RSY থেকে পাই RY2 = RS2+SY2 —(i)
সমকোণী ত্রিভুজ ∆XST থেকে পাই XT2 = XS2+ST2 —(ii)
সমকোণী ত্রিভুজ ∆XSY থেকে পাই XY2 = XS2+SY2 —(iii)
(i) নং ও (ii) নং সমীকরণ যোগ করে পাই ,
RY2 + XT2 = RS2+SY2+ XS2+ST2
বা, RY2 + XT2 = (2XS)2+XS2+SY2+(2SY)2 [যেহেতু ,RS ও ST বাহুদ্বয়ের মধ্যবিন্দু যথাক্রমে X ও Y ]
বা, RY2 + XT2 = 4XS2+XS2+SY2+4SY2
বা, RY2+XT2 = 5XS2+5SY2
বা, RY2+XT2 = 5(XS2+SY2)
বা, RY2 +XT2 = 5XY2 [(iii) নং সমীকরণ থেকে পাই ]
বা, RY2 +XT2 = 5XY2 [ প্রমাণিত ]
∴ RY2 +XT2 = 5XY2 [ প্রমাণিত ]
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২
মাধ্যমিক গণিত প্রকাশ বইয়ের সব অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
15. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.):
(i) এক ব্যাক্তি একটি স্থান থেকে 24 মিটার পশ্চিমদিকে যান এবং তারপর 10 মিটার উত্তরদিকে যান । যাত্রাস্থান থেকে ব্যাক্তির দূরত্ব
(a) 34 মিটার
(b) 17 মিটার
(c) 26 মিটার
(d) 25 মিটার
Ans:(c) 26 মিটার
সমাধানঃ
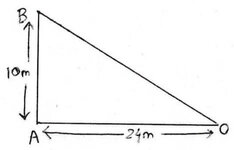
এক্ষেত্রে , OA = 24 মিটার এবং AB = 10 মিটার ।
এখন স্পষ্টতই ∆OAB সমকোণী ত্রিভুজ ।
পিথাগোরাসের উপপাদ্য থেকে পাই ,
OB2 = OA2+AB2
বা, OB2 = (24)2+(10)2
বা, OB2 = 576+100
বা, OB2 = 676
বা, OB = √676
বা, OB = 26
∴ যাত্রাস্থান থেকে ওই ব্যাক্তির দূরত্ব 26 মিটার ।
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২
(ii) ABC একটি সমবাহু ত্রিভুজ এবং AD লম্ব BC হলে , AD2 =
(a) 3/2 DC2
(b) 2 DC 2
(c ) 3DC2
(d) 4DC2
Ans: (c ) 3DC2
সমাধানঃ

ABC সমবাহু ত্রিভুজ যার AD লম্ব BC, ∴ AD মধ্যমা ।
এখন , ADC সমকোণী ত্রিভুজ থেকে পাই ,
AC2= AD2+CD2
বা, AD2 = AC2-CD2
বা, AD2 = BC2-CD2 [যেহেতু , AB=BC=CA ]
বা, AD2 = (2CD)2-CD2 [ যেহেতু , AD মধ্যমা, ∴ BC=2CD]
বা, AD2 = 4CD2-CD2
বা, AD2 = 3CD2
বা, AD2 = 3DC2
(iii) ABC সমদ্বিবাহু ত্রিভুজে AC =BC এবং AB2 =2AC2 হলে , ∠C এর পরিমাপ
(a) 30°
(b) 90°
(c ) 45°
(d) 60°
Ans: (b) 90°
সমাধানঃ
AB2 =2AC2
বা, AB2 = AC2+AC2
বা, AB2 = AC2+ BC2 [ পিথাগোরাসের উপপাদ্য ]
∴ C সমকোণ ।
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২
(iv) 13 মিটার ও 7 মিটার উচ্চ দুটি দণ্ড ভূমিতলে লম্বভাবে অবস্থিত এবং তাদের পাদদেশের মধ্যে দূরত্ব 8 মিটার । তাদের শীর্ষদেশের মধ্যে দূরত্ব
(a) 9 মিটার
(b) 10 মিটার
(c ) 11 মিটার
(d) 12 মিটার
Ans: (b) 10 মিটার
সমাধানঃ
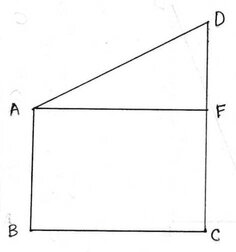
ধরাযাক , AB ও CD দুটি দণ্ড ভূমিতলে লম্বভাবে অবস্থিত ।
∴ AB = 7মিটার , CD= 13মিটার এবং BC =8 মিটার
যেহেতু , AB এবং DC উভয়ই BC ভূমির উপর লম্ব সুতরাং AB || DC , আবার A থেকে DC এর উপর AF লম্ব সুতরাং AF || BC
আবার, ∠ABC = ∠BCF = 90°
∴ ABCF একটি আয়তক্ষেত্র ।
∴ BC=AF = 8 মিটার এবং AB=FC =7 মিটার এবং AFD =90°
∆AFD সমকোণী ত্রিভুজের ক্ষেত্রে AF = 8মিটার ,DF=DC-FC=13-7=6মিটার
∆AFD সমকোণী ত্রিভুজের ক্ষেত্রে পিথাগোরাসের উপপাদ্য অনুসারে পাই,
AD2 = AF2+DF2
বা, AD2 = (8)2+ (6)2
বা, AD2 =64+36
বা, AD2 = 100
বা, AD2 = (10)2
বা, AD = 10
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
(v) একটি রম্বসের দুটি কর্ণের দৈর্ঘ্য 24 সেমি. এবং 10 সেমি. হলে , রম্বসটির পরিসীমা
(a ) 13 সেমি.
(b) 26 সেমি.
(c ) 52সেমি.
(d) 25 সেমি.
Ans: (c ) 52সেমি.
সমাধানঃ

ধরাযাক , ABCD একটি রম্বস যার দুটি কর্ণ AC ও BD পরস্পরকে O বিন্দুতে ছেদ করেছে ।
ধরি , AC = 24সেমি. এবং BD=10সেমি. , যেহেতু রম্বসের কর্ণদ্বয় পরস্পরকে O বিন্দুতে সমকোণে সমদ্বিখন্ডিত করে , ∴ OA= 24/2 সেমি. = 12 সেমি.এবং OB = 10/2 সেমি. = 5 সেমি.
এখন ∆OAB সমকোণী ত্রিভুজ থেকে পাই ,
OA2+OB2 =AB2
বা, (12)2 + (5)2 = AB2
বা, 144+25 = AB2
বা, AB2 = 169
বা, AB2 = (13)2
বা, AB= 13
∴ রম্বসের একটি বাহুর দৈর্ঘ্য 13 সেমি. সুতরাং রম্বসটির পরিসীমা = (13✕4)সেমি. = 52 সেমি.।
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২
মাধ্যমিক গণিত প্রকাশ বইয়ের সব অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
(B) নীচের বিবৃতি গুলি সত্য না মিথ্যা লিখিঃ
(i) একটি ত্রিভুজের তিনটি বাহুর দৈর্ঘ্যের অনুপাত 3:4:5 হলে , ত্রিভুজটি সর্বদা সমকোণী ত্রিভুজ হবে ।
উত্তরঃ সত্য
সমাধানঃ ধরি , ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য যথাক্রমে 3x একক , 4x একক এবং 5x একক ।
এখন , (5x)2 = 25x2 = 16x2+9x2 = (4x)2+(3x)2
∴ (5x)2 = (4x)2+(3x)2
∴ ত্রিভুজটির বাহুগুলি পিথাগোরাসের উপপাদ্যকে সমর্থন করে সুতরাং ত্রিভুজটি একটি সমকোণী ত্রিভুজ ।
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২
(ii) 10 সেমি দৈর্ঘ্যের ব্যাসার্ধবিশিষ্ট একটি বৃত্তে কোনো জ্যা কেন্দ্রে সমকোণ উৎপন্ন করলে জ্যাটির দৈর্ঘ্য 5 সেমি. হবে ।
উত্তরঃ মিথ্যা ।
সমাধানঃ
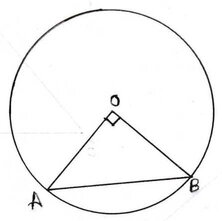
ধরাযাক,O কেন্দ্রীয় বৃত্তের AB জ্যা কেন্দ্রে সমকোণ উৎপন্ন করে । ∴ ∆AOB সমকোণী ত্রিভুজ ।
এক্ষেত্রে , OA=OB=10সেমি.
এখন , ∆AOB সমকোণী ত্রিভুজ থেকে পাই ,
AB2 = OA2+OB2
বা, AB2 = (10)2+(10)2
বা, AB2 = 100+100
বা, AB2 = 200
বা, AB = √200
বা, AB = 10√2
∴ AB জ্যাএর দৈর্ঘ্য 10√2 সেমি.
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
(C ) শূন্যস্থান পূরণ করিঃ
(i) একটি সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুটি বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলের ___________ সমান ।
উত্তরঃ সমষ্টির
Madhyamik Math Solution Of Chapter 22
(ii) একটি সমকোণী সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য 4√2 সেমি. হলে ,অতিভুজের দৈর্ঘ্য __________ সেমি. ।
উত্তরঃ 8 সেমি. ।
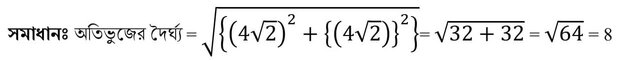
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২
(iii) ABCD আয়তকার চিত্রের AC ও BD কর্ণদ্বয় পরস্পর O বিন্দুতে ছেদ করে । AB= 12 সেমি. , AO = 6.5 সেমি. হলে, BC এর দৈর্ঘ্য ___________ সেমি. ।
উত্তরঃ 5 সেমি.
সমাধানঃ
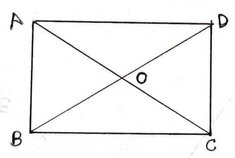
যেহেতু ,আয়তক্ষেত্রের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে, ∴ OA = OC= 6.5 সেমি.
∴ AC = (6.5✕2)সেমি. = 13 সেমি.
এখন , ∆ABC সমকোণী ত্রিভুজের ক্ষেত্রে ,
AC2 = AB2 +BC2
বা, BC2 = AC2 –AB2
বা, BC2 = (13)2 – (12)2
বা, BC2 = 169-144
বা, BC2 = 25
বা, BC2 = (5)2
বা, BC = 5
মাধ্যমিক গণিত প্রকাশ বইয়ের সব অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
16. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
(i) ∆ABC ত্রিভুজের AB=(2a-1) সেমি. ,AC= 2√(2a) সেমি. এবং BC=(2a+1) সেমি. হলে, ∠BAC এর মান হিসাব করে লিখি।
সমাধানঃ
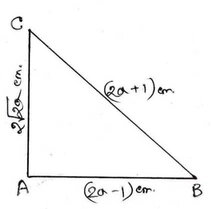
AB2+AC2 = (2a-1)2+{2√(2a)}2 = 4a2-4a+1+8a= 4a2+4a+1=(2a+1)2=BC2
∴ AB2+AC2 = BC2 [ পিথাগোরাসের উপপাদ্য ]
∴ ∆ABC সমকোণী ত্রিভুজ যার ∠A সমকোণ ।
∴ ∠A=90°
(ii) পাশের চিত্রে ∆PQR ত্রিভুজের অভ্যন্তরে O বিন্দু এমনভাবে অবস্থিত যে ∠POQ=90 ,OP=6 সেমি. এবং OQ= 8সেমি. ।যদি PR=24সেমি. এবং ∠QPR =90° হয় ,তাহলে QR বাহুর দৈর্ঘ্য কত তা লিখি ।
সমাধানঃ
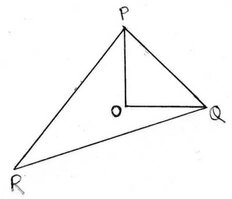
∆PQR ত্রিভুজে ∠POQ =90° , OP=6 সেমি. এবং OQ=8সেমি. ।
∆PQR সমকোণী ত্রিভুজে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই ,
PQ2 = OP2+OQ2
বা, PQ2 = (6)2 +(8)2
বা, PQ2 = 36+64
বা, PQ2 = 100
বা, PQ2=(10)2
বা, PQ = 10
আবার ∆PQR সমকোণী ত্রিভুজ যার ∠QPR=90°
∴ PR2+QP2 = RQ2
বা, (24)2+(10)2 = QR2
বা, 576 + 100 = QR2
বা, QR2 = 676
বা, QR2 = (26)2
বা, QR = 26
∴ QR বাহুর দৈর্ঘ্য 26 সেমি.।
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২
(iii) ABCD আয়তকার চিত্রের অভ্যন্তরে O বিন্দু এমনভাবে অবস্থিত যে OB=6সেমি., OD= 8 সেমি. এবং OA=5 সেমি. । OC এর দৈর্ঘ্য নির্ণয় কর ।
সমাধানঃ
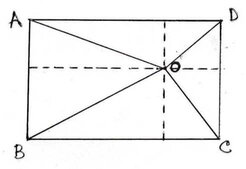
ABCD আয়তকার চিত্রের অভ্যন্তরে O একটি বিন্দু হলে , OA2+OC2 = OB2+OD2হয় ।
∴ OA2+OC2 = OB2+OD2
বা, (5)2+OC2 = (6)2+(8)2
বা, 25+OC2 = 36+64
বা, OC2 = 100-25
বা, OC2 = 75
বা, OC2 = (5√3)2
বা, OC = 5√3
∴ OC এর দৈর্ঘ্য 5√3 সেমি. ।
Koshe Dekhi 22 Class 10|পিথাগোরাসের উপপাদ্য কষে দেখি ২২
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
(iv) ∆ABC ত্রিভুজের A বিন্দু থেকে BC বাহুর উপর AD লম্ব BC বাহুর সঙ্গে D বিন্দুতে মিলিত হয় । যদি BD=8 সেমি. ,DC=2 সেমি. এবং AD = 4সেমি. হয় ,তাহলে ∠BAC এর পরিমাপ কত তা লিখি ।
সমাধানঃ
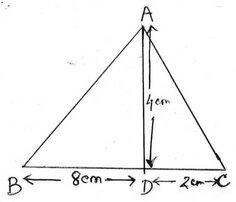
∆ABC ত্রিভুজের A বিন্দু থেকে BC বাহুর উপর AD লম্ব যা BC বাহুর সঙ্গে D বিন্দুতে মিলিত হয় ।
∴ ∆ABD এবং ∆ACD উভয়ই সমকোণী ত্রিভুজ ।
এখন , ∆ABD সমকোণী ত্রিভুজ থেকে পাই ,
AB2 = AD2+BD2
বা, AB2 = (4)2+(8)2
বা, AB2 = 16+64
বা, AB2 = 80
আবার , ∆ACD সমকোণী ত্রিভুজ থেকে পাই ,
AC2 = AD2+CD2
বা, AC2 = (4)2+(2)2
বা, AC2 = 16+4
বা, AC2 = 20
BC= BD+CD = 8+2 =10 সেমি.
আবার , ∆ABC ত্রিভুজের ক্ষেত্রে ,
AB2 +AC2 = 80+20=100=(10)2 =BC2
∴ AB2+AC2 = BC2
∴ ∆ABC সমকোণী ত্রিভুজ
∴ ∠BAC = 90º
Madhyamik Math Koshe Dekhi 22|পিথাগোরাসের উপপাদ্য কষে দেখি ২২ ক্লাস ১০ সমাধান|Koshe Dekhi 22 Class 10
(v) ∆ABC সমকোণী ত্রিভুজের ∠ABC = 90°, AB = 3সেমি. ,BC=4সেমি. এবং B বিন্দু থেকে AC বাহুর উপর লম্ব BD যা AC বাহুর সঙ্গে D বিন্দুতে মিলিত হয় । BD এর দৈর্ঘ্য নির্ণয় কর।
সমাধানঃ
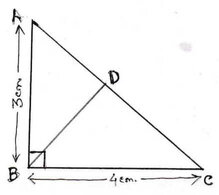
∆ABC সমকোণী ত্রিভুজের ক্ষেত্রে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই ,
AC2 = AB2+BC2
বা, AC2 = (3)2+(4)2
বা, AC2 = 9+16
বা, AC2 = 25
বা, AC2 = (5)2
বা, AC = 5
এখন , ∆ABC সমকোণী ত্রিভুজের BC ভূমি হলে AB উচ্চতা এবং AC ভূমি হলে BD উচ্চতা ।
∴ ABC ত্রিভুজের ক্ষেত্রফল = ½ ✕4✕3 বর্গসেমি = ½ ✕5✕BD বর্গসেমি
∴ ½ ✕ 4✕3 = ½ ✕5✕BD
বা, 6 = 5BD/2
বা, BD = 12/5
বা, BD = 2.4
∴ BD এর দৈর্ঘ্য 2.4 সেমি. ।
আরও দেখুনঃ মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধান
আরও দেখুনঃ মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধান
আরও দেখুনঃ মাধ্যমিকের সকল বিষয়ের মক টেস্ট
আরও দেখুনঃ WBBSE OFFICIAL SITE