Koshe Dekhi 23.2 Class 10|ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি কষে দেখি ২৩.২|কষে দেখি ২৩.২ ক্লাস ১০ সমাধান |WBBSE Madhyamik Ganit Prakash Class 10(Ten) (X) Math Solution Of Chapter 23|WB Board Class 10 Math Solution Of Chapter 23|WB Board Class 10 Math Book Solution.
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
Koshe Dekhi 23.2 Class 10|ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি কষে দেখি ২৩.২|কষে দেখি 23.2 ক্লাস 10
1. আমাদের বাড়ির জানালায় একটি মই ভূমির সঙ্গে 60° কোণে রাখা আছে । মইটি 2√3 মিটার লম্বা হলে আমাদের জানালাটি ওই ভূমি থেকে কত উপরে আছে ছবি এঁকে হিসাব করে লিখি ।
সমাধানঃ
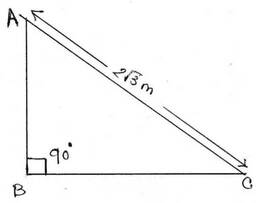
ধরাযাক AB হল ভূমি থেকে আমাদের বাড়ির জানালার উচ্চতা । AC হল মইয়ের উচ্চতা । ∴ AC = 2√3 মিটার । মইটি ভূমির সাথে 60° কোণ করেছে ।
∴ ∠ACB =60°
এখন সমকোণী ত্রিভুজ ABC থেকে পাই
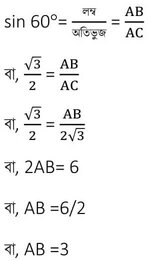
∴ ভূমি থেকে আমাদের বাড়ির জানালার উচ্চতা 3 মিটার ।
2. ABC সমকোণী ত্রিভুজের B সমকোণ । AB =8√3 সেমি. এবং BC=8 সেমি. হলে ,∠ACB ও ∠BAC –এর মান হিসাব করে লিখি ।
সমাধানঃ
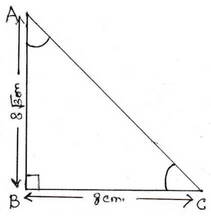
ABC সমকোণী ত্রিভুজের B সমকোণ । AB =8√3 সেমি. এবং BC=8 সেমি.। ∠ACB এর সাপেক্ষে AB উচ্চতা এবং BC ভূমি এবং AC অতিভুজ । আবার ∠BAC এর সাপেক্ষে AB ভূমি এবং BC উচ্চতা এবং AC অতিভুজ ।
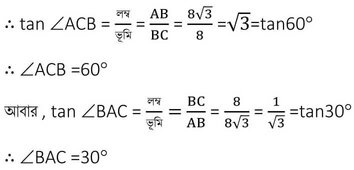
3. ABC সমকোণী ত্রিভুজের ∠B =90° , ∠A=30° এবং AC =20 সেমি. । BC এবং AB বাহুদ্বয়ের দৈর্ঘ্য হিসাব করে লিখি ।
সমাধানঃ
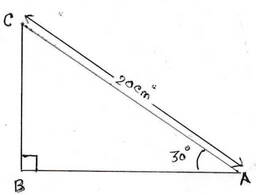
ABC সমকোণী ত্রিভুজে B =90° এবং A=30° এবং AC =20 সেমি.
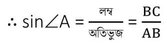

4. PQR সমকোণী ত্রিভুজের ∠Q =90° ,∠R =45° ;যদি PR =3√2 মিটার হয় ,তাহলে PQ ও QR বাহুদ্বয়ের দৈর্ঘ্য হিসাব করে লিখি ।
সমাধানঃ

PQR সমকোণী ত্রিভুজের ∠Q =90° ,∠R =45° এবং PR =3√2 মিটার
PQR ত্রিভুজের ∠R-এর সাপেক্ষে

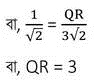
∴ QR বাহুর দৈর্ঘ্য 3 মিটার ।
5. মান নির্ণয় করিঃ
(i) sin245° -cosec260° +sec230°
সমাধানঃ
sin245° -cosec260° +sec230°
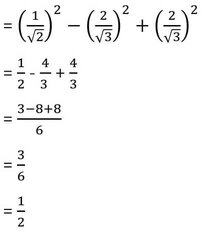
∴ sin245° -cosec260° +sec230° =1/2
(ii) sec245°-cot245°-sin230°-sin260°
সমাধানঃ
sec245°- cot245°- sin230°- sin260°
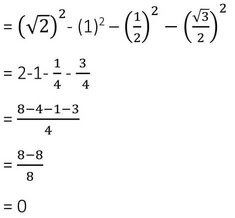
∴ sec245°- cot245°- sin230°- sin260° =0
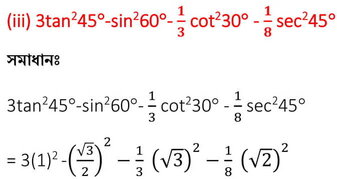
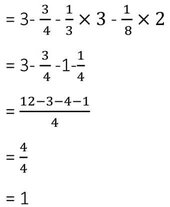
∴ 3tan245°-sin260°-(1/3) cot230° -(1/8) sec245° =1

(4/3)cot230° +3sin260°-2cosec260°- (3/4) tan230° = 3পূর্ণ 1/3
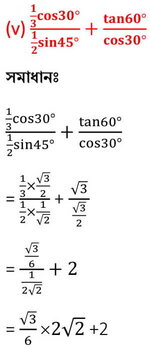
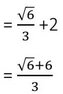
উত্তরঃ (√6+6)/3

উত্তরঃ 0

উত্তরঃ 0

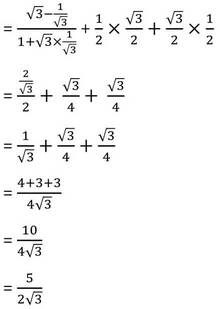
উত্তরঃ 5/2√3

উত্তরঃ 1
6. দেখাই যে ,
(i) sin245°+cos245°=1
সমাধানঃ
sin245°+cos245°
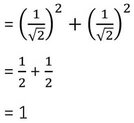
∴ sin245°+cos245°=1 [প্রমাণিত ]
(ii) cos60° =cos230°-sin230
সমাধানঃ
বামপক্ষঃ
cos60° = 1/2
ডানপক্ষঃ
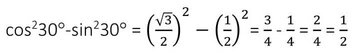
∴ cos60° =cos230°-sin230° [প্রমাণিত ]
Koshe Dekhi 23.2 Class 10|ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি কষে দেখি ২৩.২|কষে দেখি 23.2 ক্লাস 10
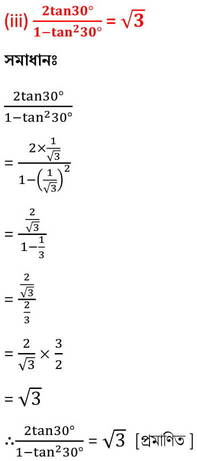

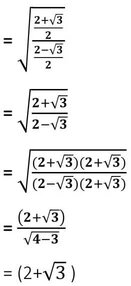
ডানপক্ষঃ
sec60° +tan60°= 2 +√3
∴ বামপক্ষ = ডানপক্ষ [প্রমাণিত ]

ডানপক্ষঃ
sec60°= 2
∴ বামপক্ষ = ডানপক্ষ [প্রমাণিত ]

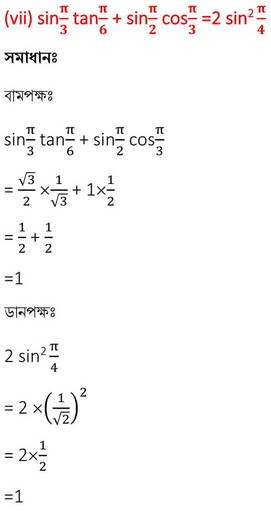
বামপক্ষ = ডানপক্ষ [প্রমাণিত]
7.(i) x sin45° cos45° tan60° =tan45°-cos60° হলে, x-এর মান নির্ণয় করি ।
সমাধানঃ
x sin45° cos45° tan60° =tan45°-cos60°
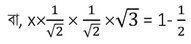
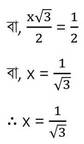
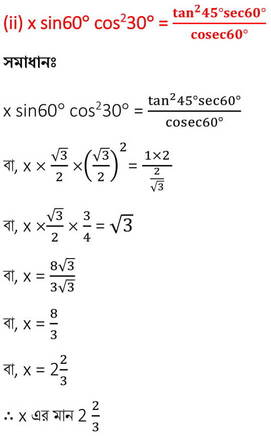
(iii) x2 = sin2 30° +4 cot2 45° -sec2 60° হলে, x এর মান নির্ণয় করি ।
সমাধানঃ
x2 = sin2 30° +4 cot2 45° -sec2 60°
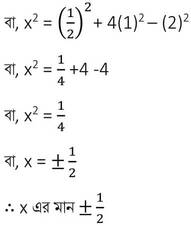
8. x tan30° +y cot60° =0 এবং 2x – y tan45° =1 হলে, x ও y –এর মান হিসাব করে লিখি ।
সমাধানঃ
প্রদত্ত সমীকরণ দুটি হল ,
x tan30° +y cot60° =0
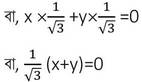
বা, x + y =0 —- (i)
এবং 2x – y tan45° =1
বা, 2x-y(1)=1
বা, 2x –y =1—(ii)
(i) ও (ii) নং সমীকরণ যোগ করে পাই ,
x+y +2x-y=1
বা, 3x =1
বা, x = 1/3
X এর প্রাপ্ত মান (i) নং সমীকরনে বসিয়ে পাই ,
x + y =0
বা, 1/3 +y =0
বা, y = -1/3
∴ নির্ণেয় সমাধান x = 1/3 এবং y =-1/3
Koshe Dekhi 23.2 Class 10|ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি কষে দেখি ২৩.২|কষে দেখি 23.2 ক্লাস 10
9. যদি A=B =45° হয় ,তবে যাচাই করি যে ,
(i) sin(A+B) =sinAcosB +cosAsinB
(ii) cos(A+B) = cosAcosB-sinAsinB
সমাধানঃ
(i) sin(A+B) =sinAcosB +cosAsinB
বামপক্ষঃ
sin(A+B)
= sin(45°+45°)
= sin90°
= 1
ডানপক্ষঃ
sinAcosB +cosAsinB
= sin45°cos45° +cos45°sin45°
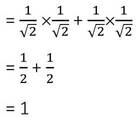
∴ sin(A+B) =sinAcosB +cosAsinB [প্রমাণিত ]
(ii) cos(A+B) = cosAcosB-sinAsinB
বামপক্ষঃ
Cos(A+B)
= cos(45°+45°)
= cos90°
= 0
ডানপক্ষঃ
cosAcosB-sinAsinB
= cos45°cos45° -sin 45°sin45°
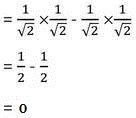
∴ বামপক্ষ = ডানপক্ষ [প্রমাণিত ]
Koshe Dekhi 23.2 Class 10|ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি কষে দেখি ২৩.২|কষে দেখি 23.2 ক্লাস 10
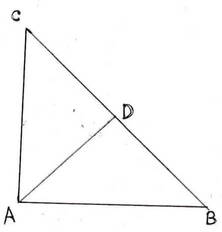
10 (i) ABC সমবাহু ত্রিভুজের BD মধ্যমা । প্রমাণ করি যে , tan∠ABD = cot∠BAD
সমাধানঃ
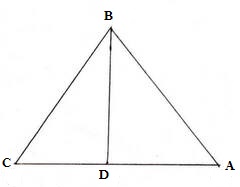
ABC সমবাহু ত্রিভুজের BD মধ্যমা ।
∴ BD ⊥ AC
∴ ABD সমকোণী ত্রিভুজ যার ∠ADB সমকোণ ।
∠ABD এর সাপেক্ষে ,
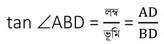
∠BAD এর সাপেক্ষে ,
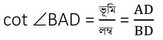
∴ tan ∠ABD = cot ∠BAD [প্রমাণিত ]

মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
11. ϴ (0° ≤ϴ≤90°) –এর কোন মান /মানগুলির জন্য 2cos2ϴ-3cosϴ+1=0 সত্য হবে নির্ণয় করি ।
সমাধানঃ
2cos2ϴ-3cosϴ+1=0
বা, 2cos2ϴ -(2+1)cosϴ+1=0
বা, 2cos2 ϴ -2cosϴ -cosϴ +1 =0
বা, 2cosϴ (cosϴ -1) -1(cosϴ -1)=0
বা, (cosϴ -1) (2cosϴ-1)=0
দুটি রাশির গুনফল শূন্য
হয় (cosϴ -1)=0
বা, cosϴ=1
বা, cosϴ= cos0°
বা, ϴ= 0°
অথবা (2cosϴ – 1)=0
বা, cosϴ = ½
বা, cosϴ = cos60°
বা, ϴ =60°
∴ ϴ -এর মান 0° বা 60°
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
Thanks for you 👉☺️
ধন্যবাদ ।
Thank you for that ☺️😊
Thank you so much
Thank you so much 🥰❤️✨
Thank you so much 🥰
Thank you so much 👍 …
May God bless you 🤞
Thanks a lo.. it help me so much 💓💓💓💓
Thanks a lot 🙏 💓 💗 💕 ❤️ ☺️