WBBSE Class 9 Math Koshe Dekhi 7.4|বহুপদী সংখ্যামালা কষে দেখি ৭.৪|গণিত প্রকাশ নবম শ্রেণি বহুপদী সংখ্যামালা কষে দেখি ৭.৪ সমাধান| বহুপদী সংখ্যামালা কষে দেখি 7.4 সমাধান |WBBSE Gonit Prokash Class 9 Math Chapter 7 Koshe dekhi 7.4 Polynomial Solution.
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
WBBSE Class 9 Math Koshe Dekhi 7.4|বহুপদী সংখ্যামালা কষে দেখি ৭.৪|গণিত প্রকাশ নবম শ্রেণি বহুপদী সংখ্যামালা কষে দেখি ৭.৪ সমাধান | বহুপদী সংখ্যামালা কষে দেখি 7.4 সমাধান | WBBSE Gonit Prokash Class 9 Math Chapter 7 Koshe dekhi 7.4 Polynomial Solution.
1. নীচের বহুপদী সংখ্যামালাগুলির মধ্যে কোনগুলির একটি উৎপাদক (x+1) হিসেব করে লিখি ।
(i) 2x3+3x2-1
(ii) x4+x3-x2+4x+5
(iii) 7x3+x2+7x+1
(iv) 3+3x-5x3-5x4
(v)x4+x2+x+1
(vi) x3+x2+x+1
সমাধানঃ
(i) ধরি , f(x) = 2x3+3x2-1
x+1 = 0
বা, x = -1
∴ (x+1) বহুপদী সংখ্যামালার শূন্য -1
∴ f(-1) = 2(-1)3+3(-1)2-1 = -2+3-1= 0
∴ গুণনীয়ক উপপাদ্য অনুসারে (x+1) , f(x) বহুপদী সংখ্যামালার একটি উৎপাদক ।
(ii) ধরি , f(x) = x4+x3-x2+4x+5
x+1= 0
বা, x = -1
∴ (x+1) বহুপদী সংখ্যামালার শূন্য -1
∴ f(-1) = (-1)4+(-1)3-(-1)2+4(-1)+5 = 1-1-1-4+5 = -5+5 = 0
∴ গুণনীয়ক উপপাদ্য অনুসারে (x+1) , f(x) বহুপদী সংখ্যামালার একটি উৎপাদক ।
(iii) ধরি , f(x) = 7x3+x2+7x+1
x+1 = 0
বা, x =-1
∴ (x+1) বহুপদী সংখ্যামালার শূন্য -1
∴ f(-1)= 7(-1)3+(-1)2+7(-1)+1 = -7+1-7+1 = -12 ≠0
∴ (x+1), f(x) = 7x3+x2+7x+1এর উৎপাদক (x+1) নয় ।
(iv) ধরি , f(x) = 3+3x-5x3-5x4
x+1 = 0
বা, x=-1
∴ (x+1) বহুপদী সংখ্যামালার শূন্য -1
∴ f(-1) = 3+3(-1) -5(-1)3 -5(-1)4 = 3-3+5-5 = 0
∴ গুণনীয়ক উপপাদ্য অনুসারে (x+1) , f(x)= 3+3x-5x3-5x4 বহুপদী সংখ্যামালার একটি উৎপাদক ।
(v) ধরি , f(x)= x4+x2+x+1
x+1 = 0
বা, x =-1
∴ (x+1) বহুপদী সংখ্যামালার শূন্য -1
∴ f(-1) = (-1)4+(-1)2+(-1)+1 = 1+1-1+1= 2 ≠ 0
∴(x+1) ,f(x) = x4+x2+x+1 বহুপদী সংখ্যামালার একটি উৎপাদক নয় ।
(vi)ধরি , f(x) = x3+x2+x+1
x+1=0
বা, x =-1
∴ (x+1) বহুপদী সংখ্যামালার শূন্য -1
∴f(-1) = (-1)3+(-1)2+(-1)+1 = -1+1-1+1 = 0
∴ গুণনীয়ক উপপাদ্য অনুসারে (x+1) , f(x)= x3+x2+x+1 বহুপদী সংখ্যামালার একটি উৎপাদক ।
2. গুণনীয়ক উপপাদ্য ব্যবহার করে নীচের বহুপদী সংখ্যামালাগুলি f(x)-এর একটি উৎপাদক g(x) কিনা লিখি ।
(i) f(x) = x4-x2-12 এবং g(x) = x+2
(ii) f(x) = 2x3+9x2-11x-30 এবং g(x) = x+5
(iii) f(x) = 2x3 +7x2 -24x -45 এবং g(x) = x-3
(iv) f(x) = 3x3+x2-20x +12 এবং g(x) = 3x-2
সমাধানঃ g(x) = x+2 =0
∴ x+2 =0
বা, x =-2
∴ g(x) বহুপদী সংখ্যামালার শূন্য -2 ।
f(x) = x4-x2-12
∴ f(-2) = (-2)4 –(-2)2 -12 =16 – 4-12 =16-16 = 0
∴গুণনীয়ক উপপাদ্য অনুসারে গুণনীয়ক উপপাদ্য অনুসারে f(x) এরএকটি উৎপাদক g(x) ।
(ii) g(x) =x+5 = 0
∴ x+5 = 0
বা, x =-5
∴ g(x) বহুপদী সংখ্যামালার শূন্য -5
f(x) =2x3+9x2-11x-30
∴ f(-5) = 2(-5)3+9(-5)2-11(-5) -30 = 2(-125) +9(25) +55 -30 = -250+225+55-30= -25+25 =0
∴ গুণনীয়ক উপপাদ্য অনুসারে f(x) এর একটি উৎপাদক g(x) ।
(iii) g(x) = x-3 = 0
∴ x-3 =0
বা, x =3
∴ g(x) বহুপদী সংখ্যামালার শূন্য 3 ।
f(x) = 2x3 +7x2 -24x -45
∴ f(3) = 2(3)3 +7(3)2-24(3) -45 = 54+63 -72 -45 = 117 – 117 =0
∴গুণনীয়ক উপপাদ্য অনুসারে f(x) এর একটি উৎপাদক g(x) ।
(iv) g(x) = 3x-2 = 0
∴ 3x-2 =0
বা, x = 2/3
∴ g(x) বহুপদী সংখ্যামালার শূন্য 2/3
f(x) = 3x3+x2-20x+12
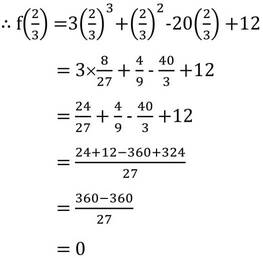
∴ গুণনীয়ক উপপাদ্য অনুসারে f(x) এর একটি উৎপাদক g(x)
3. k-এর মান কত হলে x+2 দ্বারা 2x4+3x3+2kx2+3x+6 বহুপদী সংখ্যামালাটি বিভাজ্য হবে হিসাব করে লিখি ।
সমাধানঃ ধরি , f(x) =2x4+3x3+2kx2+3x+6 এবং g(x) = x+2
g(x) = x+2 = 0
বা, x+2 =0
বা, x=-2
∴ g(x) বহুপদী সংখ্যামালার শূন্য -2
যেহেতু , f(x) বহুপদী সংখ্যামালাটি g(x) বহুপদী সংখ্যামালা দ্বারা বিভাজ্য
∴ f(-2) = 0[গুণনীয়ক উপপাদ্য অনুসারে ]
বা, 2(-2)4+3(-2)3+2k(-2)2+3(-2)+6 =0
বা, 32-24 +8k -6+6 = 0
বা, 8k +8 = 0
বা, 8k = -8
বা, k = -8/8
বা,k = -1
∴ k = -1 হলে f(x) বহুপদী সংখ্যামালা g(x) বহুপদী সংখ্যামালা দ্বারা বিভাজ্য হবে ।
4. K-এর মান কত হলে , নীচের বহুপদী সংখ্যামালাগুলি f(x) –এর একটি উৎপাদক g(x) হবে হিসেব করিঃ
(i) f(x) = 2x3+9x2+x+k এবং g(x) = x-1
(ii) f(x)= kx2-3x+k এবং g(x) = x-1
(iii) f(x) = 2x4+x3-kx2-x+6 এবং g(x) = 2x-3
(iv) f(x) = 2x3+kx2+11x+k+3 এবং g(x) = 2x-1
সমাধানঃ
(i) g(x) = x-1 =0
বা, x=1
g(x) = x-1 বহুপদী সংখ্যামালার শূন্য 1 ।
f(x) = 2x3+9x2+x+k
যেহেতু f(x) বহুপদী সংখ্যামালার একটি উৎপাদক g(x)
∴ f(1) = 0 [গুণনীয়ক উপপাদ্য অনুসারে ]
বা, 2(1)3+9(1)2+1+k =0
বা, 2+9+1+k = 0
বা, 12 +k = 0
বা, k = -12
∴ k = -12 হলে f(x) বহুপদী সংখ্যামালার একটি উৎপাদক g(x) হবে ।
(ii) g(x) = x-1 = 0
∴ x-1 =0
বা, x =1
f(x) = kx2-3x+k
যেহেতু f(x) বহুপদী সংখ্যামালার একটি উৎপাদক g(x)
∴ f(1) = 0 [গুণনীয়ক উপপাদ্য অনুসারে ]
বা, k(1)2 -3(1) + k =0
বা, k -3 +k =0
বা, 2k -3= 0
বা, 2k =3
বা, k = 3/2
∴ k = 3/2 হলে f(x) বহুপদী সংখ্যামালার একটি উৎপাদক g(x) হবে ।
(iii) g(x) = 2x-3 = 0
∴ 2x-3 =0
বা, x = 3/2
f(x) = 2x4 +x3-kx2-x+6
∴ f(3/2) = 0 [গুণনীয়ক উপপাদ্য অনুসারে ]
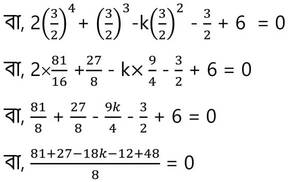
বা, 144 -18k =0
বা, 18k = 144
বা, k = 144/18
বা, k = 8
∴ k –এর মান 8 হলে f(x) –এর একটি উৎপাদক g(x) হবে ।
(iv) g(x) = 2x-1 = 0
∴ 2x-1 =0
বা, 2x = 1
বা, x = ½
f(x) = 2x3+kx2+11x+k+3
যেহেতু f(x) বহুপদী সংখ্যামালার একটি উৎপাদক g(x)
∴ f(1/2) = 0 [গুণনীয়ক উপপাদ্য অনুসারে ]
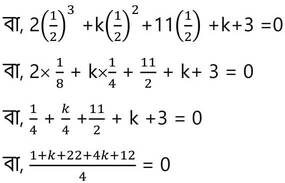
বা, 5k+35 =0
বা, 5k = -35
বা, k = -35 /5
বা, k = -7
∴ k =-7 হলে f(x) এর একটি উৎপাদক g(x) হবে ।
5. ax4+2x3-3x2+bx-4 বহুপদী সংখ্যামালার উৎপাদক x2-4 হলে a ও b এর মান হিসেব করে লিখি ।
সমাধানঃ ধরি , f(x) = ax4+2x3-3x2+bx-4
f(x) বহুপদী সংখ্যামালার উৎপাদক x2-4 = (x+2)(x-2)
ধরি , p(x) = (x+2) এবং q(x) = (x-2)
p(x) = (x+2) বহুপদী সংখ্যামালার শূন্য -2
∴ f(-2) = 0 [গুণনীয়ক উপপাদ্য অনুসারে ]
বা, a(-2)4+2(-2)3-3(-2)2+b(-2) -4 = 0
বা, 16a -16 -12 -2b -4 =0
বা,16a-2b = 32
বা, 8a – b = 16 —(i)
আবার, q(x) = x-2 বহুপদী সংখ্যামালার শূন্য 2 ।
∴ f(2) = 0 [গুণনীয়ক উপপাদ্য অনুসারে ]
বা, a(2)4+2(2)3-3(2)2+b(2) -4 = 0
বা, 16a +16 -12 +2b -4 =0
বা, 16a+2b = 0
বা, 8a+b = 0 —(ii)
(i) নং ও (ii) নং সমীকরণ যোগ করে পাই ,
16a = 16
বা, a = 16/16
বা, a = 1
a –এর প্রাপ্ত মান (ii) নং সমীকরণে বসিয়ে পাই ,
8(1)+b = 0
বা, b = -8
∴ a = 1এবং b = -8
6. x3 +3x2+2ax+b বহুপদী সংখ্যামালার দুটি উৎপাদক (x+1) ও (x+2) হলে , a ও b এর মান কত হবে হিসাব করে লিখি ।
সমাধানঃ ধরি , f(x) = x3 +3x2+2ax+b
(x+1) = 0
বা, x = -1
∴ (x+1) বহুপদী সংখ্যামালার শূন্য -1
যেহেতু , (x+1) , f(x) এর একটি উৎপাদক
∴ f(-1) =0 [গুণনীয়ক উপপাদ্য অনুসারে ]
বা, (-1)3+3(-1)2+2a(-1) +b = 0
বা, -1 +3 -2a +b = 0
বা, -2a+b = -2
বা, 2a-b = 2 —(i)
আবার , (x+2) = 0
বা , x = -2
∴ (x+2) বহুপদী সংখ্যামালার শূন্য -2
যেহেতু , (x+2) , f(x) এর একটি উৎপাদক
∴ f(-2) = 0[গুণনীয়ক উপপাদ্য অনুসারে ]
বা, (-2)3+3(-2)2+2a(-2) +b = 0
বা, -8+12 -4a + b = 0
বা, 4 -4a +b =0
বা, -4a+b = -4
বা, 4a –b = 4 —(ii)
(i) নং সমীকরণকে 2 দ্বারা গুণ করে(ii) নং সমীকরণের সাথে বিয়োগ করে পাই ,
4a-2b –(4a-b) = 4-4
বা, 4a- 2b -4a +b = 0
বা, b =0
b এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই ,
2a- b = 2
বা, 2a = 2 [ যেহেতু b = 0 ]
বা , a = 2/2
বা, a = 1
∴ a =1 এবং b = 0
7. ax3+bx2+x-6 বহুপদী সংখ্যামালাকে (x-2) দ্বারা ভাগ করলে ভাগশেষ 4 হয় এবং বহুপদী সংখ্যামালার একটি উৎপাদক (x+2) হলে a ও b এর মান কত হবে হিসাব করি ।
সমাধানঃ ধরি , f(x) = ax3+bx2+x-6
x-2 = 0
বা, x =2
∴ (x-2)বহুপদী সংখ্যামালার শূন্য 2 ।
F(x) বহুপদী সংখ্যামালাকে (x-2) দ্বারা ভাগ করলে ভাগশেষ হয় 4 ।
∴ f(2) = 4 [ভাগশেষ উপপাদ্য অনুসারে ]
বা, a(2)3+b(2)2+2-6 = 4
বা, 8a+4b -4 = 4
বা, 8a +4b = 8
বা, 4a+ b = 2 —(i)
আবার , f(x) বহুপদী সংখ্যামালার উৎপাদক (x+2)
X+2 =0
বা, x = -2
∴ (x+2)বহুপদী সংখ্যামালার শূন্য -2 ।
∴ f(-2) = 0 [গুণনীয়ক উপপাদ্য অনুসারে ]
বা, a(-2)3+b(-2)2+(-2) -6 = 0
বা, -8a+4b -8 = 0
বা, -4(2a –b +2) = 0
বা, 2a-b +2 =0
বা, 2a-b = -2 —(ii)
(i) নং ও (ii) নং সমীকরণ যোগ করে পাই ,
4a+b +2a-b = 2-2
বা, 6a = 0
বা , a = 0
a-এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই ,
4(0) +b = 2
বা, b = 2
∴ a =0 এবং b = 2
WBBSE Class 9 Math Koshe Dekhi 7.4|বহুপদী সংখ্যামালা কষে দেখি ৭.৪|গণিত প্রকাশ নবম শ্রেণি বহুপদী সংখ্যামালা কষে দেখি ৭.৪ সমাধান | বহুপদী সংখ্যামালা কষে দেখি 7.4 সমাধান
8. n – যেকোনো ধনাত্মক পূর্ণ সংখ্যা (যুগ্ম বা অযুগ্ম )হলে , দেখাই যে , xn –yn বহুপদী সংখ্যামালাটির একটি উৎপাদক x-y.
সমাধানঃ x-y = 0
বা, x = y
ধরি , f(x,y) = xn-yn
∴ ভাগশেষ f(x,x) = xn-xn = 0
যেহেতু , xn-yn কে x-y দিয়ে ভাগ করলে ভাগশেষ 0 হয় তাই xn-yn বহুপদী সংখ্যামালার একটি উৎপাদক (x-y)
9. n যেকোনো অযুগ্ম ধনাত্মক পূর্ণ সংখ্যা হলে , দেখাই যে xn+yn বহুপদী সংখ্যামালার একটি উৎপাদক (x+y)
সমাধানঃ x+y = 0
বা, x = -y
ধরি , f(x,y) = xn+yn
∴ ভাগশেষ f(-y,y) = (-y)n +yn = -yn +yn = 0 [ যেহেতু n ধনাত্মক অযুগ্ম সংখ্যা ]
যেহেতু , xn+yn কে x+y দ্বারা ভাগ করলে ভাগশেষ 0 হয় তাই xn+yn বহুপদী সংখ্যামালাটির একটি উৎপাদক x+y হবে ।
WBBSE Class 9 Math Koshe Dekhi 7.4|বহুপদী সংখ্যামালা কষে দেখি ৭.৪|গণিত প্রকাশ নবম শ্রেণি বহুপদী সংখ্যামালা কষে দেখি ৭.৪ সমাধান | বহুপদী সংখ্যামালা কষে দেখি 7.4 সমাধান
10. n যেকোনো একটি ধনাত্মক পূর্ণ সংখ্যা (যুগ্ম বা অযুগ্ম ) হলে, দেখাই যে xn+yn বহুপদী সংখ্যামালার একটি উৎপাদক কখনই x-y হবে না ।
সমাধানঃ x-y = 0
বা, x = y
ধরি , f(x,y) = xn+yn
∴ ভাগশেষ f(y,y) = yn+yn = 2yn ≠ 0
∴ xn+yn বহুপদী সংখ্যামালার একটি উৎপাদক কখনই (x-y) হবে না ।
11. বহু বিকল্পীয় প্রশ্ন (M.C.Q):
(i) x3+6x2+4x+k বহুপদী সংখ্যামালাটি (x+2) দ্বারা বিভাজ্য হলে ,k এর মান
(a) -6
(b) -7
(c ) -8
(d) -10
Ans: (c ) -8
সমাধানঃ (x+2) = 0
বা, x = -2
(x+2) বহুপদী সংখ্যামালার শূন্য -2
ধরি ,f(x) =x3+6x2+4x+k
যেহেতু , f(x) বহুপদী সংখ্যামালা (x+2) দ্বারা বিভাজ্য
∴ f(x) বহুপদী সংখ্যামালাকে (x+2) দ্বারা ভাগ করলে ভাগশেষ হবে 0 ।
∴ f(-2) = 0[ভাগশেষ উপপাদ্য অনুসারে ]
বা, (-2)3+6(-2)2+4(-2) + k = 0
বা্, -8 +24 -8 +k = 0
বা, k = -24+8+8
বা, k = -8
WBBSE Class 9 Math Koshe Dekhi 7.4|বহুপদী সংখ্যামালা কষে দেখি ৭.৪|গণিত প্রকাশ নবম শ্রেণি বহুপদী সংখ্যামালা কষে দেখি ৭.৪ সমাধান | বহুপদী সংখ্যামালা কষে দেখি 7.4 সমাধান
(ii) f(x) বহুপদী সংখ্যামালার f(-1/2 ) = 0হলে, f(x) এর একটি উৎপাদক হবে
(a) 2x-1
(b) 2x+1
(c) x-1
(d) x+1
Ans: (b) 2x+1
(iii) f(x) বহুপদী সংখ্যামালার (x-1) একটি উৎপাদক ,কিন্তু g(x) বহুপদী সংখ্যামালার উৎপাদক নয় । সুতরাং (x-1) একটি উৎপাদক হবে
(a) f(x) g(x)
(b) –f(x) +g(x)
(c ) f(x) –g(x)
(d) {f(x)+g(x)}g(x)
Ans: (a) f(x) g(x)
WBBSE Class 9 Math Koshe Dekhi 7.4|বহুপদী সংখ্যামালা কষে দেখি ৭.৪|গণিত প্রকাশ নবম শ্রেণি বহুপদী সংখ্যামালা কষে দেখি ৭.৪ সমাধান | বহুপদী সংখ্যামালা কষে দেখি 7.4 সমাধান
(iv) xn+1 বহুপদী সংখ্যামালার (x+1) একটি উৎপাদক হবে যখন
(a) n একটি অযুগ্ম ধনাত্মক পূর্ণ সংখ্যা
(b) n একটি যুগ্ম ধনাত্মক পূর্ণসংখ্যা
(c) n একটি ঋনাত্মক পূর্ণসংখ্যা
(d) n একটি ধনাত্মক পূর্ণ সংখ্যা
Ans: (a) n একটি অযুগ্ম ধনাত্মক পূর্ণ সংখ্যা
(v) an4+bn3+cn2+dn+e বহুপদী সংখ্যামালার n2-1 উৎপাদক হলে
(a) a+c+e = b+d
(b) a+b+e = c+d
(c ) a+b+c= d+e
(d) b+c+d = a+e
Ans: (a) a+c+e = b+d
সমাধানঃ n2-1 = 0
বা, n2 = 1
বা, n = ±1
∴ n2-1 বহুপদী সংখ্যামালার শূন্য 1 এবং -1 ।
ধরি , f(n) = an4+bn3+cn2+dn+e
f(n) বহুপদী সংখ্যামালার উৎপাদক (n2-1 ) = (n+1) (n-1)
∴ f(1) = 0 [গুণনীয়ক উপপাদ্য অনুসারে ]
বা, a(1)4+b(1)3+c(1)2+d(1) +e =0
বা, a+b+c+d+e = 0
এবং f(-1) = 0
বা, a(-1)4 +b(-1)3+c(-1)2 +d(-1) +e =0
বা, a-b+c-d +e =0
বা, a+c+e = b+d
WBBSE Class 9 Math Koshe Dekhi 7.4|বহুপদী সংখ্যামালা কষে দেখি ৭.৪|গণিত প্রকাশ নবম শ্রেণি বহুপদী সংখ্যামালা কষে দেখি ৭.৪ সমাধান | বহুপদী সংখ্যামালা কষে দেখি 7.4 সমাধান
12. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ
(i) x3+ax2-2x+a-12 বহুপদী সংখ্যামালার (x+a) একটি উৎপাদক হলে , a –এর মান কত হিসাব করে লিখি ।
সমাধানঃ ধরি , f(x) = x3+ax2-2x+a-12
(x+a) = 0
বা, x = -a
∴ (x+a)বহুপদী সংখ্যামালার শূন্য –a
যেহেতু ,(x+a) , f(x) বহুপদী সংখ্যামালার একটি উৎপাদক
∴ f(-a) = 0 [ গুণনীয়ক উপপাদ্য অনুসারে ]
বা, (-a)3 +a(-a)2-2(-a)+a -12 =0
বা, -a3+a3+2a+a-12 =0
বা, 3a = 12
∴ a এর মান 4 ।
WBBSE Class 9 Math Koshe Dekhi 7.4|বহুপদী সংখ্যামালা কষে দেখি ৭.৪|গণিত প্রকাশ নবম শ্রেণি বহুপদী সংখ্যামালা কষে দেখি ৭.৪ সমাধান | বহুপদী সংখ্যামালা কষে দেখি 7.4 সমাধান
(ii) k2x3 –kx2 +3kx-k বহুপদী সংখ্যামালার x-3 একটি উৎপাদক হলে ,k এর মান কত হিসাব করে লিখি ।
সমাধানঃ ধরি ,f(x) = k2x3 –kx2 +3kx-k
x-3 =0
বা, x =3
∴(x-3)বহুপদী সংখ্যামালার শূন্য 3
যেহেতু , f(x) বহুপদী সংখ্যামালার একটি উৎপাদক (x-3)
∴ f(3) = 0 [ গুণনীয়ক উপপাদ্য অনুসারে ]
বা, k2(3)3 –k(3)2 +3k(3)- k = 0
বা, 27k2 -9k +9k – k =0
বা, k(27k -1) = 0
দুটি রাশির গুনফল শূন্য
হয় , k = 0
অথবা , (27k-1) = 0
বা, k = 1/27
∴ k = 0 অথবা 1/ 27
(iii) f(x) =2x+5 হলে , f(x) +f(-x) –এর মান কত হবে লিখি ।
সমাধানঃ
f(x) =2x+5
∴ f(-x) = 2(-x) +5 = -2x+5
∴ f(x) +f(-x) = 2x+5 -2x+5 = 10
(iv) px2+5x+r বহুপদী সংখ্যামালার (x -2) এবং (x-1/2) উভয়ই উৎপাদক হলে ,p ও r-এর মধ্যে সম্পর্ক হিসেব করে লিখি ।
সমাধানঃ ধরি , f(x) = px2+5x+r
x-2 = 0
বা, x=2
∴ (x-2) বহুপদী সংখ্যামালার শূন্য 2
px2+5x+r বহুপদী সংখ্যামালার (x -2) একটি উৎপাদক ।
∴ f(2) = 0 [গুণনীয়ক উপপাদ্য অনুসারে ]
বা, p(2)2+5(2)+r = 0
বা, 4p +10 +r = 0
বা, 4p+r = -10 —(i)
আবার , (x-1/2) = 0
বা, x = ½
∴ (x-1/2) বহুপদী সংখ্যামালার শূন্য ½
px2+5x+r বহুপদী সংখ্যামালার (x -1/2) একটি উৎপাদক ।
∴ f(1/2) = 0
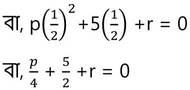
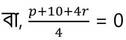
বা, 4r + p = -10 —-(ii)
(i) নং ও (ii) নং সমীকরণ তুলনা করে পাই ,
4p+r =4r+p
বা, 4p-p = 4r-r
বা, 3p = 3r
বা, p = r
∴p ও r এর মধ্যে সম্পর্ক হল p = r
WBBSE Class 9 Math Koshe Dekhi 7.4|বহুপদী সংখ্যামালা কষে দেখি ৭.৪|গণিত প্রকাশ নবম শ্রেণি বহুপদী সংখ্যামালা কষে দেখি ৭.৪ সমাধান | বহুপদী সংখ্যামালা কষে দেখি 7.4 সমাধান
(v) f(x) =2x+3 রৈখিক বহুপদী সংখ্যামালার শূন্য কত হবে লিখি ।
সমাধানঃ f(x) =2x+3
বা, 2x+3 = 0
বা, 2x = -3
বা, x = -3/2
∴ রৈখিক বহুপদী সংখ্যামালার শূন্য -3/2
WBBSE Class 9 Math Koshe Dekhi 7.4|বহুপদী সংখ্যামালা কষে দেখি ৭.৪|গণিত প্রকাশ নবম শ্রেণি বহুপদী সংখ্যামালা কষে দেখি ৭.৪ সমাধান | বহুপদী সংখ্যামালা কষে দেখি 7.4 সমাধান
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
ধন্যবাদ ।এই POST টি ভালো লাগলে SHARE করার অনুরোধ রইল । এইরকম সুন্দর সুন্দর POST পেতে ,আমাদের FACEBOOK PAGE টি LIKE করুন ।
Very useful website..