Nije Kori 12.2 Class 6 | তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু- Anushilan.Com -এর তরফ থেকে West Bengal Board -এর ষষ্ঠ শ্রেণীর ছাত্রছাত্রীদের জন্য গণিতপ্রভা ক্লাস VI বইয়ের নিজে করি 12.2 এর সমাধান এখানে দেওয়া হল । এখানে তোমরা শিখতে পারবে তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু নির্ণয়ের পদ্ধতি এবং ল.সা.গু ও গ.সা.গু সংক্রান্ত বিভিন্ন গুরুত্বপূর্ণ অঙ্ক । WBBSE Class 6 -এর গণিতপ্রভা বইয়ের নিজে করি 12.2 এর এই অঙ্কগুলি দ্বিতীয় পর্যায়ক্রমিক মূল্যায়নের জন্য খুবই গুরুত্বপূর্ণ । অঙ্কগুলো খুব সহজভাবে ছাত্রছাত্রীদের জন্য করে দেওয়া হল যাতে তারা খুব সহজেই অঙ্ক গুলো বুঝতে পারে । কোনো অঙ্ক যদি তোমাদের বুঝতে অসুবিধা হয় কমেন্টের মাধ্যমে জানাও ।
Nije Kori 12.2 Class 6|তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু
1. চারটি ঘন্টা 45 মিনিট ,1 ঘন্টা , 1 ঘন্টা 15 মিনিট ও 1 ঘন্টা 30 মিনিট অন্তর বাজে । বেলা 12 টায় ঘন্টাগুলি একসাথে বাজার ঠিক কতক্ষণ পর একসাথে বাজবে ও ওই সময়ের মধ্যে প্রতিটি ঘন্টা কতবার করে বাজবে ?
সমাধানঃ
প্রথম ঘন্টা বাজে 45 মিনিট অন্তর ।
দ্বিতীয় ঘন্টা বাজে 1 ঘন্টা = 60 মিনিট অন্তর ।
তৃতীয় ঘন্টা বাজে 1 ঘন্টা 15 মিনিট = (60 +15 )মিনিট = 75 মিনিট অন্তর ।
চতুর্থ ঘন্টা বাজে 1 ঘন্টা 30 মিনিট = (60 +30 ) মিনিট =90 মিনিট অন্তর ।
বেলা 12 টায় ঘন্টাগুলি একসাথে বাজার ঠিক যতক্ষণ পর একসাথে বাজবে , তা হল 45 মিনিট , 60 মিনিট , 75 মিনিট ও 90 মিনিটের ল.সা.গু ।

নির্ণেয় ল.সা.গু = 5 × 3 × 3 × 2 × 2 × 5 = 900
∴ 45 মিনিট , 60 মিনিট , 75 মিনিট ও 90 মিনিটের ল.সা.গু = 900 মিনিট = ( 900÷ 60 ) ঘন্টা = 15 ঘন্টা ।
সুতরাং, বেলা 12 টার সময়ে ঘন্টাগুলি একসাথে বাজার পর আবার 15 ঘন্টা পরে অর্থাৎ রাত 3 টের সময়ে ঘন্টাগুলি আবার একসাথে বাজবে ।
ওই 15 ঘন্টা অর্থাৎ 900 মিনিটের মধ্যে,
প্রথম ঘন্টা বাজবে = 900 ÷ 45 = 20 বার ।
দ্বিতীয় ঘন্টা বাজবে = 900 ÷ 60 = 15 বার ।
তৃতীয় ঘন্টা বাজবে = 900 ÷ 75 = 12 বার ।
এবং চতুর্থ ঘন্টা বাজবে = 900 ÷ 90 =10 বার ।
উত্তরঃ বেলা 12 টার সময়ে ঘন্টাগুলি একসাথে বাজার পর আবার 15 ঘন্টা পরে অর্থাৎ রাত 3 টের সময়ে ঘন্টাগুলি আবার একসাথে বাজবে ।
ওই সময়ের মধ্যে, প্রথম ঘন্টা বাজবে 20 বার । দ্বিতীয় ঘন্টা বাজবে 15 বার । তৃতীয় ঘন্টা বাজবে =12 বার । এবং চতুর্থ ঘন্টা বাজবে =10 বার ।
Nije Kori 12.2 Class 6|তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু | নিজে করি 12.2 ক্লাস 6
2. হিসাব করে দেখি চার অঙ্কের কোন ক্ষুদ্রতম সংখ্যা 12 , 15 , 20 ও 35 দ্বারা বিভাজ্য ।
সমাধানঃ যে সংখ্যাটি 12 , 15 ,20 ও 35 দ্বারা বিভাজ্য তা হল সংখ্যাগুলির ল.সা.গু ।
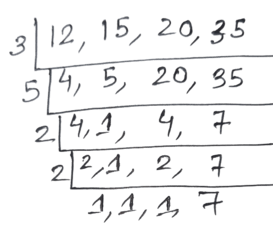
নির্ণেয় ল.সা.গু= 3×5×2×2×7 = 420
∴ 12 , 15 , 20 ও 35 এর ল.সা.গু হল 420 । অর্থাৎ 420 সংখ্যাটি 12 , 15 , 20 ও 35 দ্বারা বিভাজ্য । কিন্তু 420 সংখ্যাটি চার অঙ্কের ক্ষুদ্রতম সংখ্যা নয় ।
∴ চার অঙ্কের যে ক্ষুদ্রতম সংখ্যা যা, 12 , 15 ,20 ও 35 দ্বারা বিভাজ্য তা হল = 420 × 3 = 1260
উত্তরঃ চার অঙ্কের ক্ষুদ্রতম সংখ্যা যা 12 , 15 ,20 ও 35 দ্বারা বিভাজ্য তা হল 1260 ।
3. পাঁচ অঙ্কের বৃহত্তম সংখ্যা খুঁজি যাকে 16 , 24 , 30 ও 36 দিয়ে ভাগ করলে প্রত্যেক ক্ষেত্রে 10 ভাগশেষ থাকবে ।
সমাধানঃ 16 , 24 , 30 ও 36 দ্বারা বিভাজ্য সংখ্যাটি হল এদের ল.সা.গু । এখন , 16 , 24 , 30 ও 36 এর ল.সা.গু নির্ণয় করা যাক –
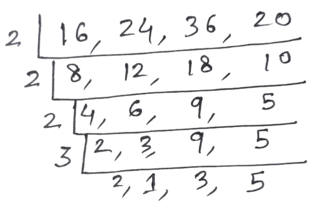
∴ নির্ণেয় ল.সা.গু = 720
এখন, পাঁচ অঙ্কের বৃহত্তম সংখ্যা যা 16 , 24 , 30 ও 36 দ্বারা বিভাজ্য তা নির্ণয় করতে হবে ।
পাঁচ অঙ্কের বৃহত্তম সংখ্যা = 99999
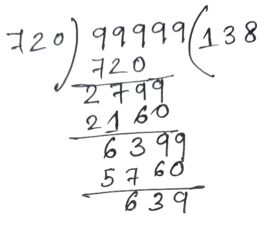
∴ পাঁচ অঙ্কের বৃহত্তম সংখ্যা যা 16 , 24 , 30 ও 36 দ্বারা বিভাজ্য তা হল = 99999 – 639 = 99360
∴ পাঁচ অঙ্কের বৃহত্তম সংখ্যা যা 16 , 24 , 30 ও 36 দ্বারা ভাগ করলে প্রতিক্ষেত্রে 10 অবশিষ্ট থাকবে তা হল = 99360 + 10 = 99370
উত্তরঃ পাঁচ অঙ্কের বৃহত্তম সংখ্যা যা 16 , 24 , 30 ও 36 দ্বারা ভাগ করলে প্রতিক্ষেত্রে 10 অবশিষ্ট থাকবে তা হল 99370 ।
Important Links
আমাদের এই POST টি, আপনাদের পছন্দ হলে Share করার অনুরোধ রইল । এইরকম আরও সুন্দর সুন্দর POST পাওয়ার জন্য আমাদের FACEBOOK PAGE টি LIKE করুন,টেলিগ্রাম চ্যানেল জয়েন করুন এবং আমাদের YouTube Channel সাবস্ক্রাইব করুন ।