Dighat Somikoron Koshe Dekhi 1.3 Class 10|দ্বিঘাত সমীকরণ সমাধান কষে দেখি ১.৩|WBBSE Madhyamik Math Class 10(Ten)(X) Chapter 1 Dighat Somikoron 1.3| গণিত প্রকাশ সমাধান ক্লাস ১০(টেন) কষে দেখি ১.৩| Ganit Prakash Class10 Koshe dekhi 1.3|Madhyamik Quadratic Equation Koshe Dekhi 1.3.
Dighat Somikoron Koshe Dekhi 1.3 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৩|কষে দেখি 1.3 ক্লাস 10
1. দুটি ধনাত্মক সংখ্যার অন্তর 3 এবং তাদের বর্গের সমষ্টি 117 । সংখ্যা দুটি হিসাব করে লিখি ।
সমাধানঃ
দুটি ধনাত্মক সংখ্যার অন্তর 3
ধরি, একটি সংখ্যা x
∴ অন্য সংখ্যা টি হবে (x+3)
শর্তানুসারে,
x2 +(x+3)2 =117
বা, x2 + x2 + 2(x)(3)+ (3)² =117
বা, 2x²+6x+9-117=0
বা, 2x²+6x-108=0
বা, x²+3x-54=0
বা, x²+(9-6)x-54=0
বা, x²+9x-6x-54=0
বা, x(x+9)-6(x+9)=0
বা, (x+9)(x-6)=0
∴ দুটি রাশির গুনফল শূন্য
হয় (x+9)=0
বা, x=-9
অথবা (x-6)=0
বা, x=6
যেহেতু সংখ্যাটি ধনাত্মক অতএব x এর ঋণাত্মক মান কে অগ্রাহ্য করে পাই
উত্তরঃ সংখ্যা দুটি হলও 6 এবং 6+3=9
2 একটি ত্রিভুজের ভূমি তার উচ্চতা দ্বিগুণ অপেক্ষা 18 মিটার বেশি ত্রিভুজের ক্ষেত্রফল 300 বর্গমিটার হলে তার উচ্চতা নির্ণয় করি ।
সমাধানঃ
ধরি, ত্রিভুজটির উচ্চতা X মিটার ।
∴ ত্রিভুজের ভূমি =(2X+18)মিটার এবং ত্রিভুজের ক্ষেত্রফল 360 বর্গমিটার
শর্তানুসারে,
1/2 × (2X+18)× X= 360 [যেহেতু ত্রিভুজের ক্ষেত্রফল =½ ×ভূমি ×উচ্চতা ]
বা, x(2x+18)=2×360
বা, 2x²+18x=720
বা, 2x²+18x-720=0
বা, x²+9x-360=0 [ উভয় পক্ষে 2 দ্বারা ভাগ করে পাই ]
বা, x²+(24-15)x-360=0
বা, x²+24x-15x-360=0
বা, x(x+24)-15(x+24)=0
বা, (x+24)(x-15)=0
যেহেতু দুটি রাশির গুনফল শূন্য
হয় (x+24)=0
বা, x=-24
অথবা (x-15)=0
বা, x=15
যেহেতু ত্রিভুজের উচ্চতা ঋণাত্মক হতে পারে না
∴ x= 15
∴ ত্রিভুজের উচ্চতা 15 মিটার ।
3. যদি একটি অখণ্ড ধনাত্মক সংখ্যার পাঁচ গুণ, তার বর্গের দ্বিগুণ অপেক্ষা 3 কম হয় তবে সংখ্যাটি নির্ণয় কর।
সমাধানঃ
ধরি, সংখ্যাটি হল x [ধনাত্মক অখণ্ড সংখ্যা]
শর্তানুসারে,
2x²-5x=3
বা, 2x²-5x-3=0
বা, 2x²-(6-1)x-3=0
বা, 2x²-6x+x-3=0
বা, 2x(x-3)+1(x-3)=0
বা, (x-3)(2x+1)=0
যেহেতু দুটি সংখ্যার গুনফল শূন্য
∴ হয় (x-3)=0
বা, x=3
অথবা (2x+1)=0
বা, x=-1/2
যেহেতু x একটি অখন্ড ধনাত্মক সংখ্যা ।
∴ x =3
∴ নির্ণেয় সংখ্যাটি হল 3 ।
4. দুটি স্থানের মধ্যে দূরত্ব 200 কিমি ; এক স্থান হতে অপর স্থানে মোটর গাড়িতে যেতে যে সময় লাগে জীপগাড়িতে যেতে তার চেয়ে 2 ঘণ্টা সময় কম লাগে । মোটরগাড়ি অপেক্ষা জিপ গাড়ির গতিবেগ ঘন্টায় 5 কিমি বেশি হলে, মোটরগাড়ির গতিবেগ হিসাব করে লিখি ।
সমাধানঃ
ধরি, মোটরগাড়ি গতিবেগ x কিমি/ঘন্টা
∴ জিপগাড়ির গতিবেগ (x+5)কিমি/ঘন্টা
এবং, অতিক্রান্ত দূরত্ব =200 কিমি

শর্তানুসারে ,

যেহেতু দুটি সংখ্যার গুনফল শূন্য
∴ হয় (x-20)=0
বা, x=20
অথবা (x+25)=0
বা, x=-25
এক্ষেত্রে গতিবেগের মান ঋণাত্মক হতে পারেনা
∴ x = 20
∴ মোটরগাড়ি গতিবেগ 20 কিমি/ঘন্টা ।
আরও দেখুনঃ মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধান
5. অমিতাদের আয়তক্ষেত্রাকার জমির ক্ষেত্রফল 2000 বর্গমিটার এবং পরিসীমা 180 মিটার । অমিতাদের আয়তক্ষেত্রাকার জমির দৈর্ঘ্য ও প্রস্থ হিসাব করে লিখি।
সমাধানঃ
অমিতাদের আয়তক্ষেত্রাকার জমির ক্ষেত্রফল 2000 বর্গমিটার এবং পরিসীমা 180 মিটার
ধরি, অমিতাদের আয়তক্ষেত্রাকার জমির দৈর্ঘ্য x মিটার অতএব প্রস্থ
(180 /2) – দৈর্ঘ্য =(90-x) মিটার
শর্তানুসারে,
x(90-x)=2000
বা, 90x-x² =2000
বা, x²-90x+2000=0
বা, x²-(50+40)x+2000=0
বা, x²-50x-40x+2000=0
বা, x(x-50)-40(x-50)=0
বা, (x-50)(x-40)=0
যেহেতু দুটি রাশির গুনফল শূন্য
∴ হয় (x-50)=0
বা, x=50
অথবা, (x-40)=0
বা, x=40
∴আয়তকার জমির দৈর্ঘ্য = 50 মিটার এবং প্রস্থ = (90-50) মিটার =40 মিটার।
6. দুই অঙ্কের একটি সংখ্যার দশকের ঘরের অংক এককের ঘরের অংক অপেক্ষা 3 কম । সংখ্যাটি থেকে উহার অংক দুটির গুনফল বিয়োগ করলে বিয়োগফল 15 হয় । সংখ্যাটির একক ঘরের অংক হিসাব করে লিখি ।
সমাধানঃ
ধরি, সংখ্যাটির এককের ঘরের অংক x
∴ সংখ্যাটির দশকের ঘরের অংক (x-3)
∴ সংখ্যাটি হবে =10(x-3)+x =11x-30
যেহেতু সংখ্যাটি থেকে উহার অঙ্কদ্বয়ের গুণফল বিয়োগ করলে বিয়োগফল 15 হয়
∴ (11x-30)-x(x-3)=15
বা, 11x-30-x²+3x-15=0
বা, -x²+14x-45=0
বা, x²-14x+45=0
বা, x²-(9+5)x+45=0
বা,x²-9x-5x+45=0
বা, x(x-9)-5(x-9)=0
বা,(x-9)(x-5)=0
দুটি সংখ্যার গুনফল শূন্য
হয় (x-9)=0
বা, x=9
অথবা, (x-5)=0
বা, x=5
∴ এককের ঘরের অঙ্ক হল 5 অথবা 9 ।
7. আমাদের স্কুলের চৌবাচ্চায় দুটি নল আছে নল দুটি দিয়ে চৌবাচ্চাটি (11পূর্ণ 1/9) মিনিটে পূর্ণ হয় ।যদি নল দুটি আলাদা ভাবে খোলা থাকে তবে চৌবাচ্চাটি ভর্তি করতে একটি নল অপর নলটি থেকে 5 মিনিট বেশি সময় নেয় ,প্রত্যেকটি নল পৃথকভাবে চৌবাচ্চা থেকে কত সময়ে পূর্ণ করবে হিসাব করে লিখি ।
সমাধানঃ
ধরি, চৌবাচ্চাটি ভর্তি করতে একটি নলের সময় লাগে x মিনিট অতএব অপর নলের সময় লাগবে (x+5) মিনিট ।
ধরি, সমগ্র চৌবাচ্চা =1 অংশ

শর্তানুসারে,

যেহেতু দুটি রাশির গুনফল শূন্য
∴ হয় (x-20)=0
বা, x=20
অথবা, (9x+25)=0
বা, x=-25/9
সময় ঋণাত্মক হওয়া অসম্ভব
∴ x=20
অর্থাৎ একটি নল চৌবাচ্চা পূর্ণ করে 20 মিনিটে
∴ অপর নল চৌবাচ্চাটি পূর্ণ করবে (20+5) মিনিটে = 25 মিনিটে
Dighat Somikoron Koshe Dekhi 1.3 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৩|কষে দেখি 1.3
আরও দেখুনঃ মাধ্যমিকের সকল বিষয়ের মক টেস্ট
8. পর্ণা ও পীযূষ কোন একটি কাজ একত্রে 4 দিনে সম্পন্ন করে । আলাদাভাবে একা কাজ করলে পর্নার যে সময় লাগবে , পীযুষের তার চেয়ে 6 দিন বেশি সময় লাগবে । পর্ণা একাকী কতদিনে কাজটি সম্পন্ন করবে করতে পারবে হিসাব করে লিখি ।
সমাধানঃ
ধরি , পর্ণা একাকী কাজটি করতে পারে x দিনে
∴ প্রদত্ত শর্তানুসারে পীযুষের সময় লাগবে (x+6) দিন
ধরি, সমগ্র কাজ = 1 অংশ

শর্তানুসারে,
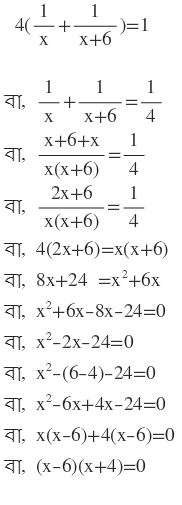
দুটি রাশির গুনফল শূন্য
∴ হয় (x-6)=0
বা, x=6
অথবা, (x+4)=0
বা, x=-4
যেহেতু সময় ঋণাত্মক হতে পারেনা ।
X=6
∴পর্ণা একাকী কাজটি করতে পারবে 6 দিনে ।
Dighat Somikoron Koshe Dekhi 1.3 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৩|কষে দেখি 1.3
9. কলমের মূল্য প্রতি ডজনে 6 টাকা কমলে 30 টাকায় আরো তিনটি বেশি কলম পাওয়া যাবে । কমার পূর্বে প্রতি ডজন কলমের মূল্য নির্ণয় করি ।
সমাধানঃ
ধরি, প্রতি ডজন কলমের মূল্য x টাকা ।

দাম হ্রাস পাওয়ার পরে প্রতি ডজন কলমের মূল্য (x-6) টাকা

শর্তানুসারে ,
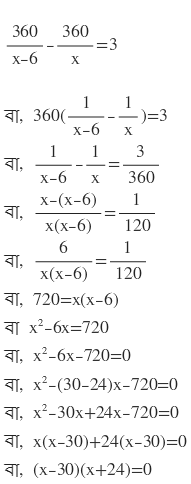
দুটি রাশির গুনফল শূন্য
∴ হয় (x-30)=0
বা, x=30
অথবা, (x+24)=0
বা, x=-24
কলমের মূল্য ঋণাত্মক হতে পারেনা , সুতরাং x=30
অর্থাৎ প্রতি ডজন কলমের মূল্য 30 টাকা ।
আরও দেখুনঃ মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধান
10. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A) :-
(A) বহুবিকল্পীয় প্রশ্ন (MCQ)
(i) একটি দ্বিঘাত সমীকরণের বীজ এর সংখ্যা
(a) একটি
(b) দুটি
(c) তিনটি
(d) কোনোটিই নয়
উত্তরঃ (b) দুটি
(ii) ax²+bx+c=0 দ্বিঘাত সমীকরণ হলে
(a) b≠0
(b) c≠0
(c) a≠0
(d) কোনোটিই নয়
উত্তরঃ (c ) a ≠ 0
(iii) একটি দ্বিঘাত সমীকরণের চলের সর্বোচ্চ ঘাত
(a) 1
(b) 2
(c) 3
(d) কোনোটিই নয়
উত্তরঃ (b) 2
(iv) 4(5x²-7x+2)=5(4x²-6x+3) সমীকরণটি
(a) রৈখিক
(b) দ্বিঘাত
(c) ত্রিঘাত
(d) কোনোটিই নয়
উত্তরঃ (a) রৈখিক
4(5x²-7x+2)=5(4x²-6x+3)
বা, 20x²-28x+8=20x²-30x+15
বা, 20x2 -20x2 -28x+30x+8-15=0
বা, 2x-7=0 [এটি একটি রৈখিক সমীকরণ ]
(v) x2/x =6 সমীকরণের বীজ/বীজদ্বয়
(a) 0
(b)6
(c) 0 ও 6
(d) -6
উত্তরঃ (b) 6
Dighat Somikoron Koshe Dekhi 1.3 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৩|কষে দেখি 1.3
(B )নিচের বিবৃতি গুলোর সত্য না মিথ্যা লিখি :-
(i) (x-3)2 = x2-6x+9 একটি দ্বিঘাত সমীকরণ ।
উত্তরঃ প্রদত্ত উক্তিটি মিথ্যা ।
(x-3)2 = x2-6x+9
বা, x2-2.x.3 +32=x2-6x+9
বা, x2-6x+9= x2-6x+9
∴ এটি একটি অভেদ ।
(ii) x²=25 সমীকরণের একটি মাত্র বীজ 5
∴ প্রদত্ত উক্তিটি মিথ্যা ।
Dighat Somikoron Koshe Dekhi 1.3 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৩|কষে দেখি 1.3
(c ) শূন্যস্থান পূরণ করি :-
(i) যদি ax²+bx+c=0 সমীকরণটির a=0 এবং b≠0 হয় , তবে সমীকরণটি একটি রৈখিক সমীকরণ ।
(ii) যদি একটি দ্বিঘাত সমীকরণের দুটি বীজই 1 হয়, তবে সমীকরণটি হল x²-2x+1=0 ।
(iii) x²=6x সমীকরণের বীজদ্বয় 0 ও 6
Dighat Somikoron Koshe Dekhi 1.3 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৩|কষে দেখি 1.3
11. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A):-
(i) x²+ax+3=0 সমীকরণের একটি বীজ 1 হলে, a- এর মান নির্ণয় করি ।
সমাধানঃ x²+ax+3=0 সমীকরণের একটি বীজ 1
∴ (1)²+a(1)+3=0
বা, 1+a+3=0
বা, a= -4
Dighat Somikoron Koshe Dekhi 1.3 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৩|কষে দেখি 1.3
(ii) x²-(2+b)x+6=0 সমীকরণের একটি বীজ 2 হলে , অপর বীজটির মান লিখি ।
সমাধানঃ x²-(2+b)x+6=0 সমীকরণের একটি বীজ 2
ধরি, অপর বীজ = a
∴ 2a=6 [ ∵ দ্বিঘাত সমীকরণের বীজদ্বয়ের গুনফল = ধ্রুবক পদ/ x2 -এর সহগ ]
বা, a = 6/2
বা, a = 3
∴ অপর বীজটির মান = 3
Dighat Somikoron Koshe Dekhi 1.3 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৩|কষে দেখি 1.3
(iii) 2x²+kx+4=0 সমীকরণের একটি বীজ 2 হলে , অপর বীজটির মান লিখি ।
সমাধানঃ ধরি, অপর বীজ = a
∴ 2a= 4/2 [ ∵ দ্বিঘাত সমীকরণের বীজদ্বয়ের গুনফল = ধ্রুবক পদ/ x2 -এর সহগ ]
বা, 2a= 2
বা, a = 1
∴ অপর বীজটির মান =1 ।
Dighat Somikoron Koshe Dekhi 1.3 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৩|কষে দেখি 1.3
(iv) একটি প্রকৃত ভগ্নাংশ ও তার অনোন্যক -এর অন্তর 9/20; সমীকরণটি লিখি ।
সমাধানঃ ধরি, প্রকৃত ভগ্নাংশ টি হল x
∴ তার অনোন্যক হবে 1/x
শর্তানুসারে,
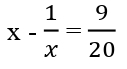
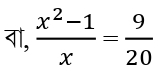
বা, 20(x²-1)= 9x
বা, 20x²-20 = 9x
বা, 20x²-9x-20=0
∴ সমীকরণ টি হল 20x²-9x-20=0 ।
Dighat Somikoron Koshe Dekhi 1.3 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৩|কষে দেখি 1.3
(v) ax²+bx+35=0 সমীকরণের বীজদ্বয় -5 ও -7 হলে, a এবং b -এর মান লিখি ।
সমাধানঃ
-5 × (-7) = 35/a [∵ দ্বিঘাত সমীকরণের বীজদ্বয়ের গুনফল = ধ্রুবক পদ/ x2 -এর সহগ ]
বা, 35 = 35/a
বা, a= 35/35
বা, a =1
আবার -5+(-7) = -b/a [∵ দ্বিঘাত সমীকরণের বীজদ্বয়ের যোগফল = -(x-এর সহগ /x2 -এর সহগ)]
বা, -5-7 = -b/1
বা, -12 =-b
বা, b =12
∴ a-এর মান 1 এবং b-এর মান 12 ।
Dighat Somikoron Koshe Dekhi 1.3 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৩|কষে দেখি 1.3
আরও দেখুনঃ
I am a student
অত্যন্ত সহজ এবং সুন্দর করে বুঝিয়ে দিলেন।