Dighat Somikoron Koshe Dekhi 1.4 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৪|WBBSE Madhyamik Class 10 (Ten) (X) Dighat Somikoron Koshe Dekhi 1.4|WBBSE Math Solution Class 10|মাধ্যমিক দ্বিঘাত সমীকরণ কষে দেখি ১.৪|গণিত প্রকাশ ক্লাস ১০(টেন) কষে দেখি ১.৪| Ganit Prakash Somadhan Class 10| Koshe Dekhi 1.4.
Dighat Somikoron Koshe Dekhi 1.4 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৪|কষে দেখি 1.4 ক্লাস 10
1(i) 4x²+(2x-1)(2x+1)= 4x(2x-1) এই সমীকরণটির সমাধানে শ্রীধর আচার্যের সূত্র প্রয়োগ করা সম্ভব কিনা বুঝে লিখি ।
সমাধানঃ
4x²+(2x-1)(2x+1)= 4x(2x-1)
বা, 4x²+ (2x)²- (1)²= 8x²-4x
বা, 4x² + 4x²-1 = 8x²-4x
বা, 8x² -1 = 8x² -4x
বা, 4x-1=0
∴ প্রদত্ত সমীকরণ টি একটি দ্বিঘাত সমীকরণ নয় সুতরাং সমীকরণটিতে শ্রীধর আচার্যের সূত্র প্রয়োগ করা সম্ভব নয় ।
Dighat Somikoron Koshe Dekhi 1.4 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৪|কষে দেখি 1.4 ক্লাস 10
1(ii) শ্রীধর আচার্যের সুত্রের সাহায্যে আমরা কোন ধরনের সমীকরণের সমাধান করতে পারি ?
উত্তরঃ একচল বিশিষ্ট দ্বিঘাত সমীকরণ ।
1(iii) 5x²+2x-7=0 সমীকরণে শ্রীধর আচার্যের সূত্র প্রয়োগ করে x=(k±12)/10 পাওয়া গেলে k এর মান কত হবে ?
সমাধানঃ
প্রদত্ত সমীকরণ টি হলও, 5x²+2x-7=0
প্রদত্ত সমীকরণ টিকে ax²+bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a= 5 , b= 2 এবং c=-7
শ্রীধর আচার্যের সূত্র প্রয়োগ করে পাই,
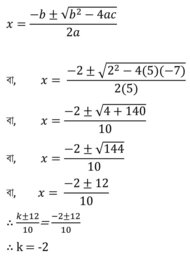
Dighat Somikoron Koshe Dekhi 1.4 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৪|কষে দেখি 1.4 ক্লাস 10
2.নিচের দ্বিঘাত সমীকরণ গুলির বাস্তব বীজ থাকলে শ্রীধর আচার্যের সূত্রের সাহায্যে সমাধান করো ।
(i) 3x2+11x-4=0
সমাধানঃ
3x2+11x-4=0
প্রদত্ত সমীকরণ টিকে ax2+bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a= 3 , b = 11 এবং c = -4
এখন ,
নিরূপক = b2-4ac= (11)2-4(3)(-4)= 22+48 = 70 > 0
∴ সমীকরণটির বাস্তব বীজ আছে ।
শ্রীধর আচার্যের সূত্র প্রয়োগ করে পাই ,
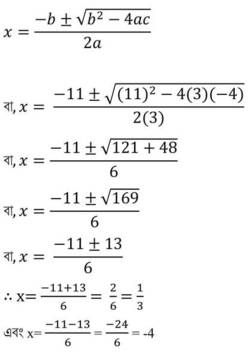
নির্ণেয় সমাধান x = 1/3 এবং x= -4
Dighat Somikoron Koshe Dekhi 1.4 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৪|কষে দেখি 1.4 ক্লাস 10
(ii) (x-2)(x+4)+9=0
সমাধানঃ
(x-2)(x+4)+9=0
বা, x(x+4)-2(x+4)+9=0
বা, x2-2x+4x-8+9=0
বা, x2 +2x+1=0
সমীকরণ টিকে ax2+bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a = 1 , b = 2 এবং c = 1
নিরূপক= b2-4ac= (2)2-4(1)(1) = 4-4=0
∴ প্রদত্ত সমীকরণটির বাস্তব বীজ আছে এবং তারা সমান ।
এখন শ্রীধর আচার্যের সূত্রের সাহায্যে সমাধান করে পাই ,
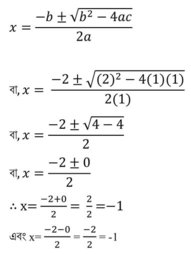
∴ নির্ণেয় সমাধান x = -1 এবং x = -1
Dighat Somikoron Koshe Dekhi 1.4 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৪|কষে দেখি 1.4 ক্লাস 10
(iii) (4x-3)2 – 2(x+3)=0
সমাধানঃ
(4x-3)2 – 2(x+3)=0
বা, (4x)2 -2 (4x) (3)+(3)2 -2x -6=0
বা, 16x2-24x+9-2x-6=0
বা, 16x2 -26x+3=0
সমীকরণ টিকে ax2+bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a = 16, b= -26 , c = 3
নিরূপক= b2-4ac = (-26)2 – 4(16)(3)= 676-192=484 > 0
∴ প্রদত্ত সমীকরণের বীজ গুলি বাস্তব ।
শ্রীধর আচার্যের সূত্র প্রয়োগ করে পাই ,
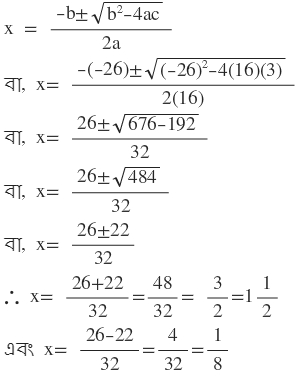
নির্ণেয় সমাধান x = 3/2 = (1 পূর্ণ 1/2) এবং x = 1/8 ।
Dighat Somikoron Koshe Dekhi 1.4 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৪|কষে দেখি 1.4 ক্লাস 10
2(iv) 3x2 +2x-1 =0
সমাধানঃ
3x2 +2x-1 =0
সমীকরণ টিকে ax2+bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a = 3 , b= 2 এবং c = -1
নিরূপক= b2-4ac = (2)2 – 4 (3)(-1)= 4+12=16 > 0
∴ প্রদত্ত সমীকরণটির বীজগুলি বাস্তব ।
এখন শ্রীধর আচার্যের সূত্র প্রয়োগ করে পাই ,
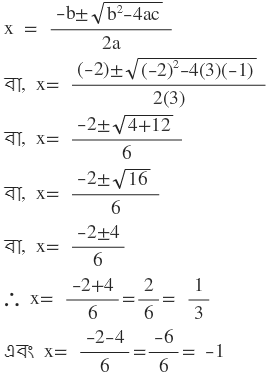
নির্ণেয় সমাধান x = 1/3 এবং x= -1
Dighat Somikoron Koshe Dekhi 1.4 Class 10|দ্বিঘাত সমীকরণ কষে দেখি ১.৪|কষে দেখি 1.4 ক্লাস 10
2(v) 3x2 +2x+1=0
সমাধানঃ
3x2 +2x+1=0
প্রদত্ত সমীকরণটিকে ax2+bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a = 3 , b = 2 এবং c = 1
নিরূপক = b2 – 4ac = (2)2 – 4(3)(1)= 4-12 = -8 < 0
সুতরাং প্রদত্ত সমীকরণটির কোনও বাস্তব বীজ নেই
2(vi) 10x2 –x -3 =0
সমাধানঃ
10x2 –x -3 =0
প্রদত্ত সমীকরণটিকে ax2+bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a = 10, b = -1 , c = -3
নিরূপক = b2 – 4ac = (-1) 2 – 4 (10) (-3) = 1+120 =121 > 0
∴ প্রদত্ত সমীকরণের বীজগুলি বাস্তব ।
শ্রীধর আচার্যের সূত্রের সাহায্যে পাই ,
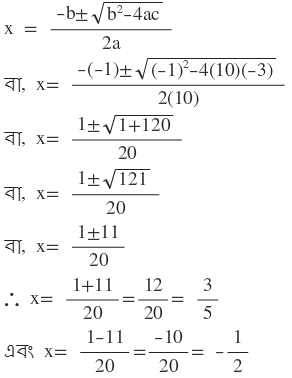
নির্ণেয় সমাধান x = -1/2 এবং x = 3/5
2.(vii) 10 x2 –x +3 =0
সমাধানঃ
10 x2 –x +3 =0
প্রদত্ত সমীকরণটিকে ax2+bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a = 10 , b = -1 , c = 3
নিরূপক = b2 – 4ac = (-1) 2 – 4 (10)(3) = 1 -120 = – 119 < 0
∴ সমীকরণের বীজগুলি কাল্পনিক ।
Dighat Somikoron Koshe Dekhi 1.4|দ্বিঘাত সমীকরণ কষে দেখি ১.৪|কষে দেখি 1.4
2(viii) 25x2 -30x +7 =0
সমাধানঃ
25x2 -30x +7 =0
প্রদত্ত সমীকরণটিকে ax2+bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a = 25 , b = -30 এবং c = 7
নিরূপক = b2 – 4ac = (-30)2 – 4(25)(7) = 900-700=200 >0
∴ সমীকরণটির বীজগুলি বাস্তব ।
শ্রীধর আচার্যের সূত্রের সাহায্যে পাই ,
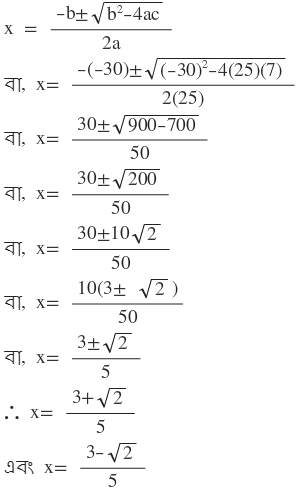
∴ নির্ণেয় সমাধান x= (3+√2)/5 এবং x= (3-√2)/5
2(ix) (4x-2)2+6x =25
সমাধান ঃ
(4x-2)2+6x =25
বা, (4x)2 – 2 (4x) (2) + (2) 2 +6x-25=0
বা, 16x2 -16x +4 +6x -25=0
বা, 16x2 -10x -21 =0
সমীকরণটিকে ax2+bx+c=0 সমীকরণের সাথে তুলনা করে পাই ,
a = 16 , b = -10 , c = -21
নিরূপক = b2 – 4ac = (-10)2 – 4 (16) (-21) = 100 + 1344 =1444 > 0
∴ সমীকরণটির বীজগুলি বাস্তব
শ্রীধর আচার্যের সূত্রের সাহায্যে পাই ,
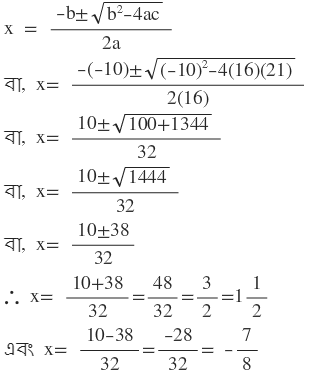
নির্ণেয় সমাধান x =3/2= 1 ½ এবং 7/8 ।
আরও দেখুনঃ মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধান
3. নিচের গানিতিক সমস্যা গুলি একচল বিশিষ্ট দ্বিঘাত সমীকরণে প্রকাশ করি এবং শ্রীধর আচার্যের সূত্রের সাহায্যে বা উৎপাদকের সাহায্যে সমাধান করিঃ-
3(i) সাথি একটি সমকোণী ত্রিভুজ অঙ্কন করেছে যার অতিভুজের দৈর্ঘ্য ক্ষুদ্রতম বাহুর দ্বিগুন অপেক্ষা 6 সেন্টিমিটার বেশি । যদি তৃতীয় বাহুর দৈর্ঘ্য অতিভুজের দৈর্ঘ্য এর থেকে 2 সেন্টিমিটার কম হয় তবে সাথির আঁকা সমকোণী ত্রিভুজের বাহু তিনটির দৈর্ঘ্য হিসাব করে লিখি ।
সমাধানঃ
ধরি , সমকোণী ত্রিভুজের ক্ষুদ্রতম বাহুর দৈর্ঘ্য x সেন্টিমিটার ।
∴ অতিভুজের দৈর্ঘ্য = (2x+6) সেন্টিমিটার ।
এবং তৃতীয় বাহুর দৈর্ঘ্য = {(2x+6)-2}= (2x+4) সেন্টিমিটার ।
সমকোণী ত্রিভুজতির ক্ষেত্রে পিথাগোরাসের উপপাদ্য প্রয়োগ করে পাই ,
(2x+6)2 = x2 + (2x+4)2
বা, (2x)2+ 2 (2x) (6) + (6)2 = x2 + (2x)2+ 2 (2x) (4) + (4)2
বা, 4x2+24x+36 = x2+4x2+16x+16
বা, 4x2 +24x +36 = 5x2+16x+16
বা, 4x2 +24x +36 -5x2 -16x -16=0
বা, -x2+8x +20=0
বা, x2-8x-20=0
বা, x2 -10x +2x -20=0
বা, x(x-10)+2(x-10)=0
বা, (x-10)(x+2)=0
দুটি রাশির গুনফল শূন্য
∴ হয় (x-10)=0
বা, x= 10
অথবা , (x+2)=0
বা, x = -2
ত্রিভুজের বাহুর দৈর্ঘ্য ঋণাত্মক হওয়া অসম্ভব ।
∴ x= 10
অতিভুজের দৈর্ঘ্য = 2x+6 = 26
তৃতীয় বাহুর দৈর্ঘ্য = 2x+4 = 24
সুতরাং ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য যথাক্রমে 10 সেন্টিমিটার , 24 সেন্টিমিটার এবং 26 সেন্টিমিটার ।
3(ii) যদি দুই অঙ্কের দুটি ধনাত্মক সংখ্যা সংখ্যাকে উহার এককের ঘরের অঙ্ক দিয়ে গুন করলে গুনফল 189 হয় এবং দশকের ঘরের অঙ্ক এককের ঘরের অঙ্কের দ্বিগুণ হয় । তবে এককের ঘরের অঙ্কটি নির্ণয় করো ।
সমাধানঃ
ধরি , এককের ঘরের অঙ্কটি হলও x ।
যেহেতু দশকের ঘরের অঙ্ক এককের ঘরের অঙ্কটির দ্বিগুন ,
∴দশকের ঘরের অঙ্কটি হবে = 2x
∴ সংখ্যাটি হবে = 10(2x) + x =21x
শর্তানুসারে ,
21x2 = 189
বা, x2 = 189/21
বা, x2 = 9
বা, x2 -9=0
বা, x2-(3)2=0
বা, (x+3)(x-3)=0
দুটি রাশির গুনফল শূন্য ।
হয়, (x+3)=0
বা, x = -3
অথবা , (x-3)=0
বা, x=3
যেহেতু সংখ্যা টি ধনাত্মক ,
এক্ষেত্রে x এর মান ঋণাত্মক হতে পারে না
∴ x =3
∴ এককের ঘরের অঙ্কটি হলও 3 ।
আরও দেখুনঃ মাধ্যমিকের সকল বিষয়ের মক টেস্ট
3(iii) সালমার গতিবেক অনিকের গতিবেগের থেকে 1 মিটার / সেকেন্ড বেশি । 180 মিটার দৌড়াতে গিয়ে সালমা অনিকের থেকে 2 সেকেন্ড আগে পৌছায়ে । অনিকের গতিবেগ প্রতি সেকেন্ড এ কত মিটার হিসাব করে লিখি ।
সমাধানঃ
ধরি , অনিকের গতিবেগ x মিটার / সেকেন্ড ।
যেহেতু সালমার গতিবেগ অনিকের গতিবেগের থেকে 1 মিটার / সেকেন্ড বেশি ,
∴ সালমার গতিবেগ (x+1) মিটার / সেকেন্ড

শর্তানুসারে ,
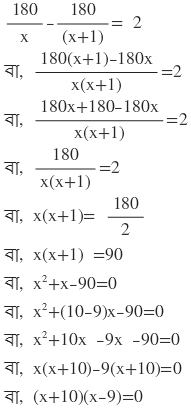
দুটি রাশির গুনফল শূন্য
∴ হয় (x+10)=0
বা, x = -10
অথবা, (x – 9)=0
বা, x = 9
এক্ষেত্রে গতিবেগের মান ঋণাত্মক হতে পারে না
∴ x = 9
∴ অনিকের গতিবেগ = 9 মিটার / সেকেন্ড ।
3(iv) আমাদের পাড়ায় একটি বর্গ ক্ষেত্রাকার পার্ক আছে । ওই পার্কের একটি বাহুর দৈর্ঘ্যের চেয়ে 5 মিটার বেশি দৈর্ঘ্য বিশিষ্ট ও ওই পার্কের বাহুর দৈর্ঘ্য থেকে 3 মিটার কম প্রস্থ বিশিষ্ট একটি আয়তক্ষেত্র কার পার্কের ক্ষেত্রফল ঐ বর্গ ক্ষেত্রাকার পার্কের ক্ষেত্রফলের দ্বিগুণ অপেক্ষা 78 বর্গ মিটার কম হলে বর্গক্ষেত্র কার পার্কের বাহুর দৈর্ঘ্য হিসাব করে লিখি ।
সমাধানঃ
ধরি , বর্গক্ষেত্র কার পার্কের প্রতিটি বাহুর দৈর্ঘ্য x মিটার ।
∴ বর্গক্ষেত্রকার পার্কের ক্ষেত্রফল x2 বর্গমিটার ।
∴ আয়তক্ষেত্রাকার পার্কের দৈর্ঘ্য (x+5) মিটার এবং আয়তক্ষেত্রের প্রস্থ (x -3) মিটার ।
∴ আয়তক্ষেত্রাকার পার্কের ক্ষেত্রফল (x+5) (x-3) বর্গমিটার ।
যেহেতু আয়তক্ষেত্রের ক্ষেত্রফল বর্গ ক্ষেত্রের ক্ষেত্রফলের দ্বিগুণ অপেক্ষা 78 বর্গ মিটার কম ,
শর্তানুসারে ,

দুটি রাশির গুনফল শূন্য
∴ হয় (x-9)=0
বা, x = 9
অথবা, (x+7)=0
বা, x = -7
যেহেতু বর্গক্ষেত্রের বাহুর দৈর্ঘ্য ঋণাত্মক হতে পারেনা ,
∴ x = 9
অর্থাৎ বর্গ ক্ষেত্রের প্রতিটি বাহুর দৈর্ঘ্য 9 মিটার ।
3(v) আমাদের গ্রামে প্রলয়বাবু তার আয়তক্ষেত্রাকার জমিতে লাগানোর জন্য মোট 350 লঙ্কার চারা কিনলেন । সারি ধরে চারা গাছ লাগাতে গিয়ে দেখলেন যে প্রতি সারিতে সারির সংখ্যার থেকে 24 টি করে বেশি গাছ লাগালে আরও দশটি গাছ অতিরিক্ত থাকে । সারির সংখ্যা হিসাব করে লিখি ।
সমাধান
ধরি , জমিতে সারির সংখ্যা x টি ।
মোট চারা গাছের সংখ্যা 350 টি ।
প্রতি সারিতে সারির সংখ্যা থেকে 24 করে বেশি গাছ লাগালে আরও 10 টি গাছ অতিরিক্ত থাকে ।

আবার প্রতি সারিতে গাছের সংখ্যা = (x+24) টি ।
শর্তানুসারে ,

দুটি রাশির গুনফল শূন্য ,
হয় (x+34)=0
বা, x = -34
অথবা, (x -10)=0
বা, x= 10
যেহেতু সারির সংখ্যা ঋণাত্মক হতে পারেনা ,
∴ x = 10
অর্থাৎ সারির সংখ্যা 10 টি ।
3(vi) জোসেফ ও কুন্তল একটি কারখানায় কাজ করে । জোসেফ একটি জিনিস তৈরি করতে কুন্তাল এর চেয়ে 5 মিনিট সময় কম নেয় । 6 ঘণ্টা কাজ করে জোশেপ কুন্তলের চেয়ে 6 টি জিনিস বেশি তৈরি করে । কুন্তল ওই একি সময় কয়টি জিনিস তৈরি করে হিসাব করে লিখি ।
সমাধানঃ
ধরি, একটি জিনিস তৈরি করতে কুন্তাল এর সময় লাগে x মিনিট ।
∴ জোশেপের সময় লাগে (x-5) মিনিট ।

শর্তানুসারে ,

দুটি রাশির গুনফল শূন্য ,
হয় (x-20)=0
বা, x=20
অথবা, (x+15)=0
বা, x = -15
যেহেতু সময় ঋণাত্মক হতে পারে না ,
∴ এক্ষেত্রে x = 20
সুতরাং 1 টি জিনিস তৈরি করতে কুন্তলের সময় লাগে 20 মিনিট ।
∴ কুন্তল ওই সময় অর্থাৎ 6 ঘণ্টায়ে তৈরি করবে 360/x = 360/20 = 18 টি জিনিস ।
3(vii) স্থির জলে একটি নৌকার গতিবেগ 8 কিমি প্রতি ঘন্টা । নৌকাটি 5 ঘণ্টায় স্রোতের অনুকূলে 15 কিমি এবং স্রোতের প্রতিকূলে 22 কিমি গেলে স্রোতের বেগ কত ছিল হিসাব করে লিখি ।
সমাধানঃ
ধরি ,স্রোতের গতিবেগ x কিমি /ঘন্টা ।
স্থির জলে নৌকার গতিবেগ 8 কিমি / ঘন্টা ।
∴ স্রোতের অনুকূলে নৌকার গতিবেগ (8+x) কিমি/ ঘণ্টা ।
এবং স্রোতের প্রতিকূলে নৌকার গতিবেগ (8-x) কিমি/ঘন্ট।

শর্তানুসারে ,

দুটি রাশির গুনফল শূন্য ,

গতিবেগ এক্ষেত্রে ঋণাত্মক হতে পারে না ।
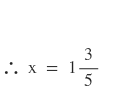
অর্থাৎ স্রোতের বেগ = (1পূর্ণ 3/5) কিমি / ঘণ্টা ।
3(viii) একটি সুপারফাস্ট ট্রেন একটি এক্সপ্রেস ট্রেনের থেকে ঘন্টায় 15 কিমি বেশি বেগে যায় ।একই সঙ্গে একটি স্টেশন থেকে ছেড়ে 180 কিমি দূরে অন্য একটি স্টেশনে সুপারফাস্ট ট্রেন টি 1 ঘন্টা আগে পৌঁছালো । সুপারফাস্ট ট্রেনটির গতিবেগ ঘন্টায় কত কিমি ছিল হিসাব করে লিখি ।
সমাধানঃ
ধরি , সুপারফাস্ট ট্রেনটির গতিবেগ x কিমি প্রতি ঘন্টা ।
∴ এক্সপ্রেস ট্রেনের গতিবেগ (x-15) কিমি প্রতি ঘন্টা ।

শর্তানুসারে,
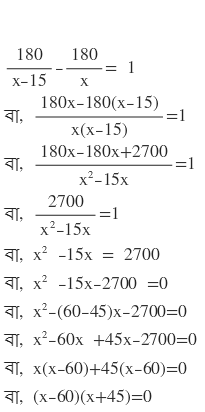
দুটি রাশির গুনফল শূন্য ,
হয় (x-60)=0
বা, x =60
অথবা (x +45)=0
বা, x = -45
এক্ষেত্রে গতিবেগ ঋণাত্মক হতে পারে না ।
x = 60
সুতরাং সুপারফাস্ট ট্রেনের গতিবেগ ঘণ্টায়ে 60 কিমি ।
3(ix) রেহানা বাজারে গিয়ে দেখল প্রতি কিগ্রা মাছের যা দাম , ডালের দাম তা থেকে প্রতি কিগ্রা 20 টাকা কম এবং চালের দাম প্রতি কেজি 40 টাকা কম । রেহেনা 240 টাকার মাছ ও 240 টাকার ডাল কিনে মোট যে পরিমান মাছ ও ডাল পেল তা 280 টাকায় চাল কেনার পরিমানের সমান । রেহেনা প্রতি কিগ্রা মাছ কি দামে কিনেছিল হিসাব করি ।
সমাধানঃ
ধরি, প্রতি কিগ্রা মাছের দাম x টাকা ।
অর্থাৎ ,

আবার, প্রতি কিগ্রা ডালের দাম (x -20) টাকা ।
অর্থাৎ ,

এবং প্রতি কিগ্রা চালের দাম (x-40) টাকা ।
অর্থাৎ ,

শর্তানুসারে ,

দুটি রাশির গুনফল শূন্য ,
হয় (x-80)=0
বা, x = 80
অথবা (x-12)=0
বা, x = 12
কিন্তু এক্ষেত্রে x এর মান 12 হতে পারে না,অর্থাৎ প্রতি কিগ্রা মাছের দাম 12 টাকা হতে পারে না ।
সুতরাং x = 80
∴ প্রতি কিগ্রা মাছের দাম 80 টাকা ।
আরও দেখুনঃ