Koshe Dekhi 12 Class VI | কষে দেখি 12 ক্লাস 6 | তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু -Anushilan.Com -এর তরফ থেকে West Bengal Board -এর ষষ্ঠ শ্রেণীর ছাত্রছাত্রীদের জন্য গণিতপ্রভা ক্লাস VI বইয়ের কষে দেখি 12 এর সমাধান (11 থেকে 24) এখানে দেওয়া হল । এখানে তোমরা শিখতে পারবে তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু নির্ণয়ের পদ্ধতি এবং ল.সা.গু ও গ.সা.গু সংক্রান্ত বিভিন্ন গুরুত্বপূর্ণ অঙ্ক । WBBSE Class 6 -এর গণিতপ্রভা বইয়ের কষে দেখি 12 এর এই অঙ্কগুলি দ্বিতীয় পর্যায়ক্রমিক মূল্যায়নের জন্য খুবই গুরুত্বপূর্ণ । অঙ্কগুলো খুব সহজভাবে ছাত্রছাত্রীদের জন্য করে দেওয়া হল যাতে তারা খুব সহজেই অঙ্ক গুলো বুঝতে পারে । কোনো অঙ্ক যদি তোমাদের বুঝতে অসুবিধা হয় কমেন্টের মাধ্যমে জানাও ।
Koshe Dekhi 12 Class VI | কষে দেখি 12 ক্লাস 6
পার্ট -1 (1 থেকে 10 পর্যন্ত অঙ্কের সমাধান)
[Click Here]
পার্ট -2 ( 11 থেকে 24 পর্যন্ত অঙ্কের সমাধান এখানে দেওয়া হল )
11. নীচের রাশিগুলির ল.সা.গু. ও গ.সা.গু.-এর মান খুঁজি।
(ক) 6 টাকা 50 পয়সা, 5 টাকা 20 পয়সা এবং 7 টাকা 80 পয়সা।
সমাধানঃ
6 টাকা 50 পয়সা = {(6 ×100)+50} পয়সা = 650 পয়সা
5 টাকা 20 পয়সা = {(5 ×100 )+ 20} = 520 পয়সা
7 টাকা 80 পয়সা = {(7 ×100 )+80} = 780 পয়সা
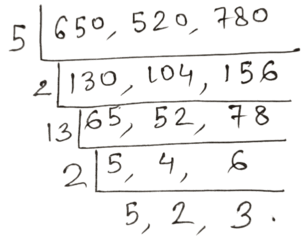
∴ নির্ণেয় ল.সা.গু = 2 × 2 × 2 ×3×5 ×5 ×13 = 7800 পয়সা = 78 টাকা
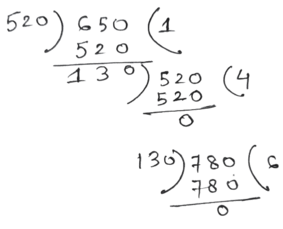
∴ নির্ণেয় গ.সা.গু= 130 পয়সা = 1 টাকা 30 পয়সা
(খ) 2 মি 28 সেমি, 3 মি. 42 সেমি এবং 4 মি. 56 সেমি।
2 মি 28 সেমি = {(2 ×100 ) +28 } সেমি. = 228 সেমি.
3 মি. 42 সেমি = {(3×100)+42 } সেমি. = 342 সেমি.
4 মি. 56 সেমি = {(4×100)+56} সেমি. = 456 সেমি.
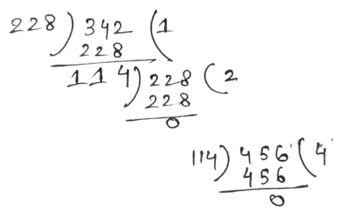
∴ নির্ণেয় গ.সা.গু = 114 সেমি. =1 মি. 14 সেমি.
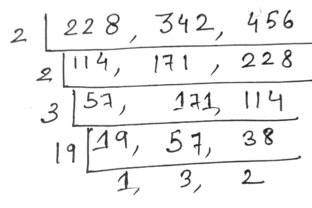
∴ নির্ণেয় ল.সা.গু = 2 × 2 × 3 ×19 × 3 × 2 = 1368 সেমি. = 1300 সেমি. + 68 সেমি. = 13 মি. 68 সেমি.
(গ) 3 লি 600 মিলিলি, 4 লি. 800 মিলিলি এবং 6 লি
সমাধানঃ
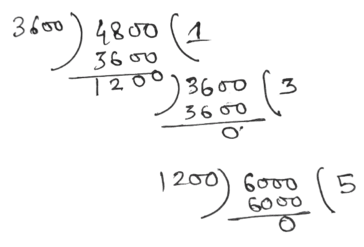
নির্ণেয় গ.সা.গু = 1200 মিলিলি. = 1000 মিলিলি. + 200 মিলিলি. = 1 লিটার 200 মিলিলিটার
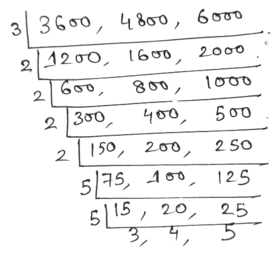
নির্ণেয় ল.সা.গু = 2×2×2×2×3×3×5×5×5×4 = 72000 মিলিলি. = 72 লিটার
(ঘ) 6 ঘণ্টা 4 মিনিট 30 সেকেন্ড, 2 ঘণ্টা 42 মিনিট।
সমাধানঃ
6 ঘন্টা 4 মিনিট 30 সেকেন্ড
= {(6×3600) + (4×60) + 30} সেকেন্ড
= (21600 +240 +30 ) সেকেন্ড
= 21870 সেকেন্ড
2 ঘন্টা 42 মিনিট
= {(2×3600)+(42×60)} সেকেন্ড
= (7200 + 2520) সেকেন্ড
= 9720 সেকেন্ড
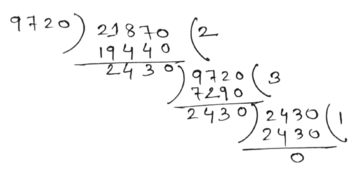
নির্ণেয় গ.সা.গু = 2430 সেকেন্ড = 2400 সেকেন্ড + 30 সেকেন্ড = 40 মিনিট 30 সেকেন্ড
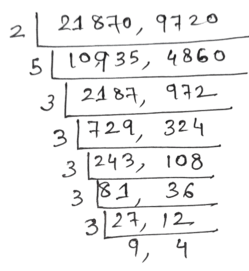
নির্ণেয় ল.সা.গু = 87480 সেকেন্ড = 87480 ÷ 3600 = 24.3 ঘন্টা = 24 ঘন্টা + ০.3 ঘন্টা = 24 ঘন্টা + (0.3 × 60) মিনিট = 24 ঘন্টা 18 মিনিট
Koshe Dekhi 12 Class VI | কষে দেখি 12 ক্লাস 6 | তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু
12. নীচের সংখ্যাজোড়াগুলির ক্ষেত্রে যাচাই করি যে , সংখ্যাদুটির গুণফল তাদের ল.সা.গু ও গ.সা.গু –এর গুণফলের সমান কিনা ।
(a) 87 , 145
সমাধানঃ
87 = 29 × 3
145 = 29 × 5
∴ এদের গ.সা.গু = 29 এবং ল.সা.গু = 29 × 3 × 5 = 435
এখন সংখ্যাদুটির ল.সা.গু × গ.সা.গু = 29 × 435 = 12615
এবং সংখ্যাগুলির গুনফল = 87 × 145 = 12615
∴ সংখ্যাদুটির ল.সা.গু × গ.সা.গু = সংখ্যাদুটির গুণফল (প্রমাণিত)
(b) 60 , 75
সমাধানঃ
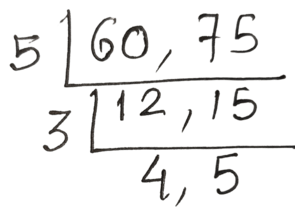
নির্ণেয় গ.সা.গু = 5×3 = 15
আবার নির্ণেয় ল.সা.গু = 5 × 3 × 4 × 5 = 300
∴ ল.সা.গু × গ.সা.গু = 15 × 300 = 4500
এবং সংখ্যাদুটির গুণফল = 60 ×75 = 4500
∴ সংখ্যাদুটির গুনফল = ল.সা.গু ×গ.সা.গু (প্রমাণিত)
(c ) 42 , 63
সমাধানঃ
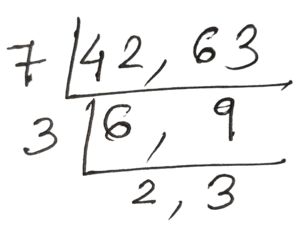
নির্ণেয় গ.সা.গু = 7×3 = 21
নির্ণেয় ল.সা.গু = 7 × 3 × 2 × 3 = 126
∴ ল.সা.গু × গ.সা.গু = 21 × 126 = 2646
সংখ্যা দুটির গুণফল = 42 × 63 = 2646
∴ সংখ্যা দুটির গুনফল = ল.সা.গু × গ.সা.গু (প্রমাণিত)
(d) 186 , 403
সমাধানঃ
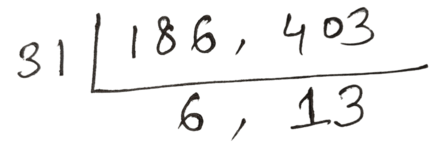
নির্ণেয় গ.সা.গু = 31
নির্ণেয় ল.সা.গু = 31 × 6 × 13 = 2418
∴ ল.সা.গু × গ.সা.গু = 2418 × 31 = 74958
এবং সংখ্যাদুটির গুনফল = 186 × 403 = 74958
সুতরাং , ল.সা.গু × গ.সা.গু = সংখ্যা দুটির গুনফল (প্রমাণিত)
13. দুটি সংখ্যার ল.সা.গু ও গ.সা.গু যথাক্রমে 2175 এবং 145 ; যদি একটি সংখ্যা 725 হয় , তাহলে অপর সংখ্যাটি কত হিসাব করি ।
সমাধানঃ আমরা জানি ,
সংখ্যা দুটির ল.সা.গু × গ.সা.গু = সংখ্যাদুটির গুনফল
∴ 2175 × 145 = 725 × অপর সংখ্যা
বা, অপর সংখ্যা = (2175 × 145) / 725
বা, অপর সংখ্যা = 435
উত্তরঃ একটি সংখ্যা 725 হলে অপর সংখ্যা হবে 435 ।
14. 145 ও 232 সংখ্যা দুটির গ.সা.গু –এর মান খুঁজি ও ওই গ.সা.গু –এর সাহায্যে ল.সা.গু –এর মান খোঁজার চেষ্টা করি ।
সমাধানঃ
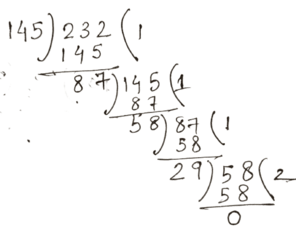
∴ 145 ও 232 –এর গ.সা.গু = 29
এবং সংখ্যা দুটির গুণফল = 145 × 232 = 33640
আমরা জানি ,
সংখ্যাদ্বয়ের গুণফল = সংখ্যা দুটির ল.সা.গু × গ.সা.গু
বা, 33640 = ল.সা.গু × 29
বা, ল.সা.গু = 33640 /29
বা, ল.সা.গু = 1160
উত্তরঃ সংখ্যাদুটির ল.সা.গু = 1160
15. 144 ও 384 সংখ্যাদুটির ল.সা.গু –এর মান খুঁজি ও ওই ল.সা.গু-এর সাহায্যে গ.সা.গু –এর মান খোঁজার চেষ্টা করি ।
সমাধানঃ
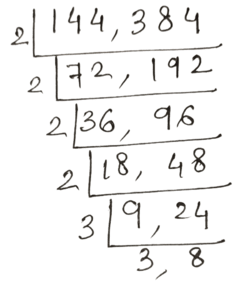
∴ 144 ও 384 সংখ্যাদুটির ল.সা.গু = 2×2×2×2×3×3×8 = 1152
সংখ্যাদুটির গুণফল = 144 × 384 = 55296
আমরা জানি ,
সংখ্যা দুটির গুণফল = ল.সা.গু × গ.সা.গু
বা, 55296 = 1152 × গ.সা.গু
বা, গ.সা.গু = 55296 ÷1152
বা, গ.সা.গু = 48
উত্তরঃ 144 ও 384 এর গ.সা.গু = 48
Koshe Dekhi 12 Class VI | কষে দেখি 12 ক্লাস 6 | তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু
16. 5834 থেকে কোন ক্ষুদ্রতম সংখ্যা বিয়োগ করলে বিয়োগফল 20 , 28 , 32 ও 35 দিয়ে বিভাজ্য হবে ?
সমাধানঃ
20 , 285 , 32 এবং 35 এর উৎপাদকে বিশ্লেষণ করে পাই ,
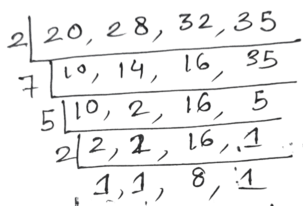
∴ নির্ণেয় ল.সা.গু = 2× 2 ×5 ×7 ×8 = 1120
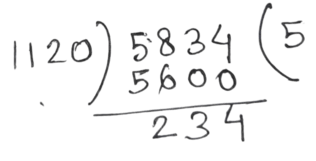
∴ 20 , 28 , 32 ও 35 দিয়ে বিভাজ্য ক্ষুদ্রতম সংখ্যাটি হল = 5834 – 234 = 5600
উত্তরঃ 5834 থেকে ক্ষুদ্রতম সংখ্যা 234 বিয়োগ করলে বিয়োগফল 20 , 28 , 32 ও 35 দিয়ে বিভাজ্য হবে ।
17. কোন বৃহত্তম সংখ্যা দিয়ে 2300 ও 3500 কে ভাগ করলে যথাক্রমে 32 ও 56 ভাগশেষ থাকবে হিসাব করি ।
(2300 -32 ) = 2268
(3500 -56 ) = 3444
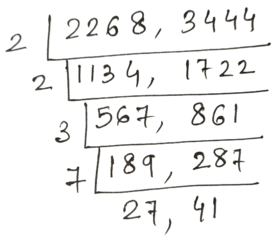
∴ নির্ণেয় গ.সা.গু = 2 × 2 × 3 × 7 = 84
উত্তরঃ নির্ণেয় বৃহত্তম সংখ্যাটি হল 84 যা দিয়ে 2300 ও 3500 কে ভাগ করলে যথাক্রমে 32 ও 56 ভাগশেষ থাকবে ।
18. হিসাব করে দেখি কোন বৃহত্তম সংখ্যা দিয়ে 650 , 775 ও 1250 কে ভাগ করলে প্রতিক্ষেত্রে একই ভাগশেষ থাকবে হিসাব করি ।
সমাধানঃ 650 , 775 ও 1250 –এদের গ.সা.গু হল সেই বৃহত্তম সংখ্যা যা দিয়ে প্রদত্ত সংখ্যাগুলিকে ভাগ করলে ভাগশেষ একই হবে ।
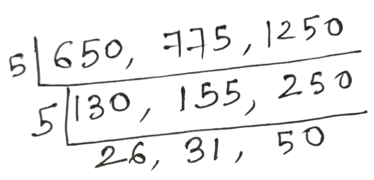
∴ 650 , 775 ও 1250 এর গ.সা.গু হল 25
উত্তরঃ 25 দিয়ে 650 , 775 এবং 1250 কে ভাগ করলে প্রতিক্ষেত্রে একই ভাগশেষ থাকবে ।
Koshe Dekhi 12 Class VI | কষে দেখি 12 ক্লাস 6 | তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু
19. দুটি সংখ্যার যোগফল 384 এবং সংখ্যাদুটির গ.সা.গু 48 ; সংখ্যাদুটি কী কী হতে পারে হিসাব করি ।
সমাধানঃ
384 ÷ 48 = 8
এখন 8 কে দুটি সংখ্যার যোগফল আকারে প্রকাশ করি
8 = 1 + 7
বা, 8 = 2 + 6
বা, 8 = 3 +5
বা, 8 = 4 + 4
এবার সংখ্যা জোড় থেকে মৌলিক সংখ্যা জোড় নিলে গ.সা.গু 48 থাকবে ।
∴ সংখ্যা জোড় গুলি হবে
= (48×1 , 48×7) অথবা (48×3 , 48×5)
= (48 , 336) অথবা (144 , 240 )
উত্তরঃ সংখ্যাদুটি হতে পারে (48 , 336) অথবা (144 , 240 ) ।
20. দুটি সংখ্যার গ.সা.গু. ও ল.সা.গু. যথাক্রমে 12 ও 720 হিসাব করে দেখি এরকম কত জোড়া সংখ্যা হতে পারে এবং সম্ভাব্য সংখ্যাগুলি কী কী ?
সমাধানঃ
সংখ্যা দুটির গুনফল = তাদের লসাগু এবং গসাগু এর গুনফল
= 12 x 720 = 8640
আমরা জানি, গসাগু হল উভয় সংখ্যার গুণনীয়ক । তাহলে ছোট সংখ্যাটি হবে গসাগু 12 এর গুনিতক।
ছোট সংখ্যাটি কী হতে পারে তার তালিকা করি।
12, 24, 36, 48, 60, 72 এবং 84
এবার দেখা যাক অন্য সংখ্যটি কী হতে পারে।
8640 ÷ 12 = 720
8640 ÷ 24 = 360
8640 ÷ 36 = 240
8640 ÷ 48 = 180
8640 ÷ 60 = 144
8640 ÷ 72 = 120
8640 ÷ 84 = পূর্ণসংখ্যা নয়
এবার দেখি কোন জোড়া সংখ্যার গ.সা.গু 12 এবং লসাগু 720
12 এবং 720 এর গসাগু 12, লসাগু 720
24 এবং 360 এর গসাগু 24, লসাগু 360 সুতরাং এরা বাদ।
36 এবং 240 এর গসাগু 12, লসাগু 720
48 এবং 180 এর গসাগু 12, লসাগু 720
60 এবং 144 এর গসাগু 12, লসাগু 720
72 এবং 120 এর গসাগু 24, লসাগু 360 সুতরাং এরা বাদ।
অর্থাৎ আমরা 4 জোড়া ভিন্ন উত্তর পাচ্ছি। সেগুলো হল-
(12, 720 ) , (48, 180) , (36, 240) এবং (60, 144)
21. কোন ক্ষুদ্রতম সংখ্যা থেকে 4000 বিয়োগ করলে বিয়োগফল 7 11 ও 13 দিয়ে বিভাজ্য হবে হিসাব করি।
সমাধানঃ
7, 11 ও 13 এর ল.সা.গু = 7 × 11 × 13= 1001
∴ ক্ষুদ্রতম সংখ্যাটি হল = 4000 + 1001= 5001
উত্তরঃ নির্ণেয় ক্ষুদ্রতম সংখ্যাটি হল 5001 যা থেকে 4000 বিয়োগ করলে বিয়োগফল 7, 11 ও 13 দিয়ে বিভাজ্য হবে।
22. 50 ও 100-এর মধ্যবর্তী দু-জোড় সংখ্যা খুঁজি যাদের গ.সা.গু. 16
সমাধানঃ
প্রদত্ত, 50 ও 100-এর মধ্যবর্তী সংখ্যা যাদের গ.সা.গু. 16 হবে।
সুতরাং, সংখ্যাগুলি 50 থেকে বড় ও 100 থেকে ছোট হবে এবং অবশ্যই 16 এর গুণিতক হবে।
∴ সংখ্যাগুলি হবে
16 × 4 = 64
16 × 5 = 80
16 × 6 =96
উত্তরঃ 50 ও 100-এর মধ্যবর্তী দু-জোড় সংখ্যা যাদের গ.সা.গু. 16 তারা হবে (64, 80) ও (80, 96)
Koshe Dekhi 12 Class VI | কষে দেখি 12 ক্লাস 6 | তিনটি সংখ্যার গ.সা.গু ও ল.সা.গু
23. 28, 33, 42 ও 77 দ্বারা বিভাজ্য যে সংখ্যাটি 98765 -এর নিকটতম তা হিসাব করে খুঁজে বার করি।
সমাধানঃ

∴ 28, 33, 42 ও 77 এর ল.সা.গু = 2 × 2 × 3 × 7 × 11 = 924
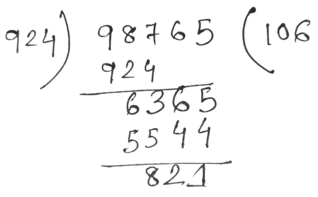
∴ 98765 -এর নিকটতম সংখ্যা
= 98765 + (924 − 821)
= 98765 + 103
= 98896
উত্তরঃ নির্ণেয় নিকটতম সংখ্যাটি হল 98868
24. হিসাব করে 13 দিয়ে বিভাজ্য এমন ক্ষুদ্রতম সংখ্যা খুঁজি যা 8, 12, 16, ও 20 দিয়ে ভাগ করলে প্রতিক্ষেত্রে 1 ভাগশেষ থাকে।
সমাধানঃ
8, 12, 16, ও 20 এর ল.সা.গু
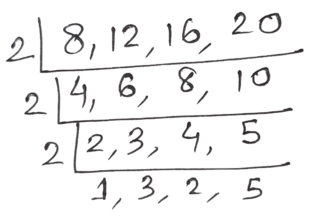
2 × 2 × 2 × 2 × 3 × 5 = 240
240×1 + 1 = 241 (13 দিয়ে বিভাজ্য নয় )
240 × 2 + 1 = 481 (13 দিয়ে বিভাজ্য )
উত্তরঃ নির্ণেয় ক্ষুদ্রতম সংখ্যা 481 যা 13 দিয়ে বিভাজ্য।
Important Links
আমাদের এই POST টি, আপনাদের পছন্দ হলে Share করার অনুরোধ রইল । এইরকম আরও সুন্দর সুন্দর POST পাওয়ার জন্য আমাদের FACEBOOK PAGE টি LIKE করুন,টেলিগ্রাম চ্যানেল জয়েন করুন এবং আমাদের YouTube Channel সাবস্ক্রাইব করুন ।