Koshe Dekhi 23.1 Class 10|ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি কষে দেখি ২৩.১ ক্লাস ১০ সমাধান|Koshe Dekhi 23.1 Class 10| WBBSE Madhyamik Ganit Prakash Class 10(Ten) (X) Math Solution Of Chapter 23|WB Board Class 10 Math Solution In Bengali|Ganit Prakash Class 10 Chapter 23 Solution.
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
Koshe Dekhi 23.1 Class 10|ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি কষে দেখি ২৩.১|কষে দেখি 23.1 ক্লাস 10
1. একটি সমকোণী ত্রিভুজ এঁকেছি যার অতিভুজ AB=10 সেমি. ,ভূমি BC=8 সেমি. এবং লম্ব AC =6সেমি. । ∠ABC –এর Sine এবং tangent এর মান নির্ণয় করি ।
সমাধানঃ
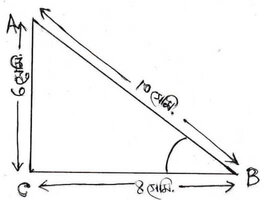
সমকোণী ত্রিভুজ ABC-তে ∠ABC এর সাপেক্ষে , অতিভুজ AB=10 সেমি. ,ভূমি BC=8 সেমি. এবং লম্ব AC =6সেমি. ।

Koshe Dekhi 23.1 Class 10|ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি কষে দেখি ২৩.১
2. সোমা একটি সমকোণী ত্রিভুজ ABC এঁকেছে যার ∠ABC =90°,AB=24সেমি. এবং BC =7 সেমি. ।হিসাব করে sinA ,cosA,tanA ও cosecA- এর মান লিখি ।
সমাধানঃ
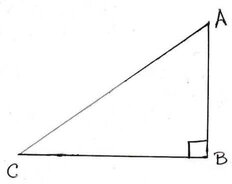
সমকোণী ত্রিভুজ ABC এর কোণ ∠A এর সাপেক্ষে ভূমি AB =24মিটার এবং লম্ব BC =7 মিটার এবং অতিভুজ AC ।
পিথাগোরাসের উপপাদ্য থেকে পাই ,
(অতিভুজ)2 = (লম্ব)2 + (ভূমি)2
বা, (AC)2 = (BC)2 + (AB)2
বা, (AC)2 = 49+576
বা, (AC)2 = 625
বা, (AC)2 = (25)2
বা, AC = 25
∴ অতিভুজ AC =25 সেমি.

3.যদি ABC একটি সমকোণী ত্রিভুজের ∠C =90°,BC =21 একক এবং AB=29 একক হয় তাহলে SinA,CosA,SinB ও CosB এর মান নির্ণয় করি ।
সমাধানঃ
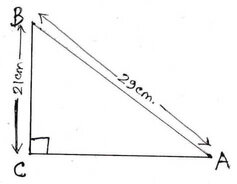
ABC সমকোণী ত্রিভুজের ∠C=90°,BC =21 একক এবং AB=29একক ।
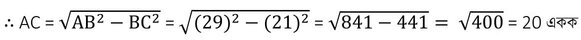
∠A এর সাপেক্ষে ভূমি AC এবং লম্ব BC এবং অতিভুজ AB আবার B কোণের সাপেক্ষে লম্ব AC এবং ভূমি BC এবং অতিভুজ AB

4. যদি cos ϴ=7/25 হয়, তাহলে ϴ কোণের সকল ত্রিকোণমিতিক অনুপাত নির্ণয় করি ।
সমাধানঃ

ধরি , ভূমি = 7k এবং অতিভুজ = 25k [k(≠0) একটি আনুপাতিক ধ্রুবক ]
পিথাগোরাসের উপপাদ্য থেকে পাই ,
(অতিভুজ)2 =(লম্ব)2+(ভূমি)2
বা, (25k)2 = (লম্ব)2 +(7k)2
বা, (লম্ব)2 = 625k2-49k2
বা, (লম্ব)2 = 576k2
বা, (লম্ব)2 = (24k)2
বা, লম্ব = 24k

5. যদি cotϴ =2 হয়, তাহলে tanϴ ও secϴ -এর মান নির্ণয় করি এবং দেখাই যে , 1+tan2ϴ=sec2ϴ

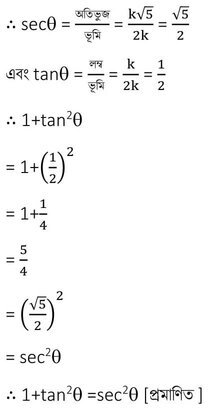
6. cosϴ = 0.6 হলে, দেখাই যে ,(5sinϴ-3tanϴ)=0
সমাধানঃ
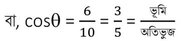
ধরি , ভূমি =3k এবং অতিভুজ =5k [k(≠0) একটি আনুপাতিক ধ্রুবক ]
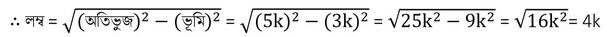
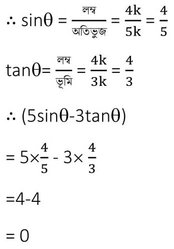
∴ (5sinϴ-3tanϴ)=0 [প্রমাণিত ]
7. যদি , cotA =4/7.5 হয় , তাহলে cosA এবং cosecA –এর মান নির্ণয় করি এবং দেখাই যে , 1+cot2A=cosec2A

8. যদি sinC =2/3 হয় , তবে cosC ✕ cosecC –এর মান হিসাব করে লিখি ।
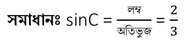
ধরি , লম্ব =2k এবং অতিভুজ =3k [k(≠0) একটি আনুপাতিক ধ্রুবক ]
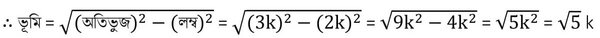

মাধ্যমিক পরীক্ষার বিগত বছরের প্রশ্নের সমাধানের জন্য এখানে CLICK করুন
9. নীচের বিবৃতিগুলি সত্য না মিথ্যা তা যুক্তি সহকারে লিখি ।
(i) tanA এর মান সর্বদা 1 অপেক্ষা বড় ।
উত্তরঃ মিথ্যা ।
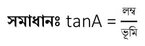
এখন লম্ব < ভূমি হলে tanA<1 হবে সুতরাং বিবৃতিটি মিথ্যা ।
Koshe Dekhi 23.1 Class 10|ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি কষে দেখি ২৩.১
(ii) cotA এর মান 1 অপেক্ষা ছোট ।
উত্তরঃ মিথ্যা।

এখন ভূমি > লম্ব হলে cotA > 1 হবে সুতরাং বিবৃতিটি মিথ্যা
(iii) একটি কোণ ϴ-এর জন্য sinϴ = 4/3 হতে পারে ।
উত্তরঃ মিথ্যা ।
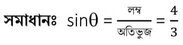
এক্ষেত্রে লম্ব 4 একক হলে অতিভুজ 3 একক কিন্তু কোনো একটি সমকোণী ত্রিভুজে লম্ব অপেক্ষা অতিভুজ ছোট হতে পারে না ।
∴ sinϴ = 4/3 হতে পারে না ।
(iv) একটি কোণ α -এর জন্য secα=12/5 হতে পারে না ।
উত্তরঃ মিথ্যা ।
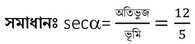
একটি সমকোণী ত্রিভুজের অতিভুজ 12 একক হলে ভূমি 5 একক হওয়া সম্ভব ।
সুতরাং বিবৃতিটি মিথ্যা ।
(V) একটি কোণ β (Beta) –এর জন্য cosecβ=5/13 হতে পারে ।
উত্তরঃ মিথ্যা ।
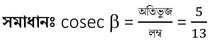
অর্থাৎ অতিভুজ 5 একক হলে লম্ব 13 একক যা অসম্ভব কারণ সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য সর্বাধিক ।
∴ cosec β =5/13 হতে পারে না ।
(vi) একটি কোণ ϴ-এর জন্য cosϴ =3/5 হতে পারে ।
উত্তরঃ সত্য ।
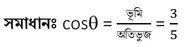
∴ ভূমি 3 একক হলে অতিভুজ 5 একক হতে পারে ।
সুতরাং cosϴ =3/5 হতে পারে ।
Koshe Dekhi 23.1 Class 10|ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি কষে দেখি ২৩.১
Very nice
Anko puro Mmmmmmmmmm