SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
অতি সংক্ষিপ্ত উত্তরধর্মী ( প্রতিটি প্রশ্নের মান 2 )
1. উদাহরণ সহ সংজ্ঞা দাওঃ
(i) সেট
(ii) সসীম বা অসীম সেট
(iii) শূন্য সেট
(iv) সার্বিক সেট
(v) একপদী সেট
(vi) সমান সেট
(vii) উপসেট ও যথার্থ উপসেট
(viii) দুটি সেটের যোগ
সমাধানঃ
(i) সেট – বস্তু সমূহের সংকলন বা সমষ্টিকে সেট আখ্যা দেওয়া হয় যখন
(a) সংকলনটি সুসংজ্ঞাত (well defined )
(b) সংকলনের অন্তর্গত যেকোনো দুটি বস্তু পরস্পর ভিন্ন (different)।
(c) সংকলনের অন্তর্গত বস্তুগুলো ক্রম নিরপেক্ষ (independent of order)
(ii) সসীম সেট – যে সেটের পদ সমূহের সংখ্যা গননার দ্বারা নির্ণয় করা সম্ভব অর্থাৎ যে সেটের পদসংখ্যা সসীম তাকে সসীম সেট বলে ।
যেমন x= {1,2,3,4}
অসীম সেট – যে সেটের পদ সমূহের সংখ্যা গননার দ্বারা নির্ণয় করা সম্ভব নয় অর্থাৎ যে সেটের পদ সংখ্যা অসীম তাকে অসীম সেট বলে ।
যেমনঃ Y = {1,2,3,4,5,6,7,…………..}
(iii) শূন্য সেট – নির্দিষ্ট নিয়ম বা ধরমের ওপর ভিত্তি করে সংজ্ঞাত কোনও সেটের যদি কোনও পদ না থাকে তাকে শূন্য সেট বলে ।
যেমন – A={ x: x একটি অখণ্ড সংখ্যা এবং 2<x<3}
(iv) সার্বিক সেট – সেট সম্পর্কিত আলোচনায় কোনও বিসেশ সংজ্ঞাধীনে আলচ্য সেট সমূহ একটি নির্দিষ্ট বৃহত্তর সেটের উপসেট হিসাবে ধরা হয় । এই নির্দিষ্ট বৃহত্তর সেটটিকে আলোচ্য সেটগুলির সাপেক্ষে সার্বিক সেট বলে । এই সার্বিক সেট কে S বা U অক্ষর দ্বারা সূচিত করা হয় ।
ধরাযাক সেট A = {0,1,2,3,4}
এবং সেট B হল = { 1,3,5,7}
A ও B সাপেক্ষে U = { 0,1,2,3,4,5,6,7,8} সেট টি হল সার্বিক সেট কারণ উভয় ক্ষেত্রে দুটি সেট A এবং B , U এর সাবসেট ।
(v) একপদী সেট – যে সেটে একটি মাত্র পদ থাকে তাকে একপদী সেট বলে ।
যেমন A = {4}
(vi) সমান সেট – দুটি সেট A ও B এমন হয় যে A সেটের প্রত্যেক পদ B সেটের প্রত্যেক পদ A সেটেরও পদ এবং A সেটের প্রত্যেক পদ B সেটেরও পদ হয় তখন A ও B দুটি সেটকে সমান সেট বলে ।
যেমনঃ x= { -2,-1} এবং Y = {a : a হল a2+3a+2 সমীকরণের বীজ }
(vii) উপসেট – দুটি সেট A ও B এমন হয় যে B সেটের প্রত্যেক পদ A সেটেরও পদ হয় তখন B সেটকে A সেটের উপসেট বলে । একে B ⊆ A আকারে প্রকাশ করা হয় ।
যেমনঃ A ={1,2,3,4,5,6} এবং B= {1,3,5} ∴ B ⊆ A
যথার্থ উপসেটঃ A ও B দুটি সেট এমন হয় যে , B সেটের প্রত্যেকটি পদ A সেটেরও পদ হয় এবং A সেটে কমপক্ষে একটি পদ এমন থাকে যে পদটি B সেটের অন্তর্গত নয় তখন B সেটকে A সেটের যথার্থ উপসেট বলে ।
∴ এক্ষেত্রে B ⊂ A
(viii) দুটি সেটের যোগ – দুটি সেট A ও B , এখন একটি সেট এমন ভাবে গঠিত হয় যে , সেই সেটটির পদ A এর পদ , B এর পদ বা A ও B উভয় সেটেরই পদ হবে । দুটি সেটের যোগ কে A U B দ্বারা প্রকাশ করা হয় ।
যেমনঃ A = {2,4,6,8,10 } এবং B = { 1,2,3,4,5,6}
A ∪ B = {2,4,6,8,10 } ∪ { 1,2,3,4,5,6} = {1,2,3,4,5,6,8,10}
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
SN Dey Class 11 Semester -1 সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
2. পার্থক্য নিরূপণ করঃ
(i) শূন্য সেট ও সার্বিক সেট
(ii) উপসেট ও প্রকৃত উপসেট
(iii) দুটি সেটের যোগ ও ছেদ
(iv) দুটি সেটের যোগ ও অন্তর
(v) সার্বিক সেট ও পূরক সেট
সমাধানঃ
শূন্য সেট ও সার্বিক সেট – নির্দিষ্ট নিয়ম বা ধর্মের ওপর ভিত্তি করে সংজ্ঞাত কোনও সেটের যদি কোনও পদ নাথাকে তাকে শূন্য সেট বলে ।
যেমন – A={ x: x একটি অখণ্ড সংখ্যা এবং 2<x<3}
সেট সম্পর্কিত আলোচনায় কোনও বিসেশ সংজ্ঞাধীনে আলচ্য সেট সমূহ একটি নির্দিষ্ট বৃহত্তর সেটের উপসেট হিসাবে ধরা হয় । এই নির্দিষ্ট বৃহত্তর সেটটিকে আলোচ্য সেটগুলির সাপেক্ষে সার্বিক সেট বলে । এই সার্বিক সেট কে S বা U অক্ষর দ্বারা সূচিত করা হয় ।
ধরাযাক সেট A = {0,1,2,3,4}
এবং সেট B হল = { 1,3,5,7}
A ও B সাপেক্ষে U = { 0,1,2,3,4,5,6,7,8} সেট টি হল সার্বিক সেট কারণ উভয় ক্ষেত্রে দুটি সেট A এবং B , U এর সাবসেট ।
অর্থাৎ শূন্য সেট এ একটিও পদ না থাকলেও সার্বিক সেট এ কমপক্ষে একটি পদ থাকতে হবে , আবার শূন্য সেট যেকোনো সেটের সাবসেট হতে পারে কিন্তু সার্বিক সেট যেকোনো সেটের সাবসেট হতে পারে না ।শূন্য সেট কে Φ দ্বারা নির্দেশ করা হয় এবং সার্বিক সেট কে U দ্বারা নির্দেশ করা হয় ।
(ii) উপসেট এবং প্রকৃত উপসেট
উপসেট – দুটি সেট A ও B এমন হয় যে B সেটের প্রত্যেক পদ A সেটেরও পদ হয় তখন B সেটকে A সেটের উপসেট বলে । একে B ⊆ A আকারে প্রকাশ করা হয় ।এক্ষেত্রে A সেট এবং B সেট সমান হতেও পারে ।
প্রকৃত উপসেট-A ও B দুটি সেট এমন হয় যে , B সেটের প্রত্যেকটি পদ A সেটেরও পদ হয় এবং A সেটে কমপক্ষে একটি পদ এমন থাকে যে পদটি B সেটের অন্তর্গত নয় তখন B সেটকে A সেটের প্রকৃত উপসেট বলে । এক্ষেত্রে B ⊂ A আকারে প্রকাশ করা হয় । এক্ষেত্রে A সেট এবং B সেট কখনই সমান হয় না ।
(iii) দুটি সেটের যোগ ও ছেদ- দুটি সেটের যোগ – দুটি সেট A ও B , এখন একটি সেট এমন ভাবে গঠিত হয় যে , সেই সেটটির পদ A এর পদ , B এর পদ বা A ও B উভয় সেটেরই পদ হবে । দুটি সেটের যোগ কে A ∪ B দ্বারা প্রকাশ করা হয় ।
অপরপক্ষে দুটি প্রদত্ত সেট A ও B এর সাধারণ পদসমূহ নিয়ে গঠিত সেটকে A ও B সেটের ছেদ বলে এবং এটি A ∩ B দ্বারা প্রকাশ করা হয় ।
A ∪ U = U হয় কিন্তু A ∩ U = A হয় ।
A ⊆ A ∪ B কিন্তু A ∩ B ⊆ A হয় ।
A ∪ Φ = A হয় কিন্তু A ∩ Φ = Φ হয় ।
(iv) দুটি সেটের যোগ ও অন্তর- দুটি সেট A ও B , এখন একটি সেট এমন ভাবে গঠিত হয় যে , সেই সেটটির পদ A এর পদ , B এর পদ বা A ও B উভয় সেটেরই পদ হবে । দুটি সেটের যোগ কে A ∪ B দ্বারা প্রকাশ করা হয় ।
যদি A ও B দুটি প্রদত্ত সেট হয় এবং একটি সেট এরূপে গঠিত হয় যে সেটির পদসমূহ A সেটের পদ কিন্তু B সেটের পদ নয় তখন গঠিত সেটটিকে A ও B সেটের অন্তর বলে , একে A-B দ্বারা নির্দেশ করা হয় ।
A ⊆ A ∪ B কিন্তু A – B ⊆ A
B ⊆ A ∪ B কিন্তু A – B ⊆ B
আবার A – B = (A ∪ B)-B
(v) সার্বিক সেট ও পূরক সেট – সেট সম্পর্কিত আলোচনায় কোনও বিসেশ সংজ্ঞাধীনে আলচ্য সেট সমূহ একটি নির্দিষ্ট বৃহত্তর সেটের উপসেট হিসাবে ধরা হয় । এই নির্দিষ্ট বৃহত্তর সেটটিকে আলোচ্য সেটগুলির সাপেক্ষে সার্বিক সেট বলে । এই সার্বিক সেট কে S বা U অক্ষর দ্বারা সূচিত করা হয়
যদি কোনও একটি সুসংজ্ঞাত সেট A এর সার্বিক সেট U হয় এবং একটি সেট এমনভাবে গঠিত হয় যে সেটির পদসমূহ U এর পদ কিন্তু A এর পদ নয় , তবে গঠিত সেটটিকে A সেটের পূরক সেট বলে । একে Ac দ্বারা প্রকাশ করা হয় ।
∴ Ac = U –A কিন্তু U c = Φ
SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
3. প্রমান করো যে প্রত্যেক সেট তার নিজের উপসেট ।
প্রমানঃ যদি A একটি প্রদত্ত সেট হয় তবে প্রমান করতে হবে যে A ⊆ A । যদি সম্ভব হয় মনে করো A ⊈ A । সুতরাং A সেটে কমপক্ষে একটি পদ আছে , যা A সেটের পদ নয়- যা অসম্ভব । ∴ A ⊆ A ( প্রমানিত )
4. দেখাও যে শূন্য সেট সব সেটের উপসেট ।
প্রমানঃ যদি A যেকোনো একটি প্রদত্ত সেট হয় , তবে প্রমান করতে হবে যে , Φ ⊆ A এখানে Φ হল শূন্য সেট । যদি সম্ভব হয় মনে করো Φ ⊈ A ।
স্পষ্টতই Φ , A সেটের উপসেট নয় বলে Φ সেটে কমপক্ষে একটি পদ আছে যেটি A সেটের পদ নয় ; কিন্তু সংজ্ঞা অনুযায়ী Φ সেটে কোনও পদ থাকেনা , সুতরাং Φ ⊈ A এই কল্পনা সত্য হতে পারেনা ।
∴ Φ ⊆ A (প্রমানিত )
5. সংক্ষিপ্ত টীকা লেখোঃ
(i) সূচক সেট (ii) ভেন চিত্র (iii) দ্বিত নীতি
(i) সূচক সেট – যে সেটের পদসমূহ একটি প্রদত্ত সেট A সেটের উপসেট , তাকে প্রদত্ত সেটের সূচক সেট বলে এবং একে P(A) দ্বারা প্রকাশ করা হয় । P(A) = { X : X ⊆ A }
যদি A = {a ,b,c } হয় তবে A সেটের উপসেট সমূহ হয় –
(i) শূন্য সেট Φ ।
(ii) {a}, {b},{c}
(iii) {a,b}, {b,c}, {c,a}
(iv) {a ,b,c}=A
∴ P(A) = { Φ , {a}, {b},{c},{a,b}, {b,c}, {c,a},{a ,b,c} }
A সেটের পদসংখ্যা n হলে P(A) সেটের পদ সংখ্যা হবে 2 n ।
(ii) ভেন চিত্র – যে চিত্রের সাহায্যে সেট প্রক্রিয়াসমূহ উপস্থাপিত করা হয় ,তাকে ভেন চিত্র বলে ।
এই প্রকার চিত্রের সাহায্যে সেট প্রক্রিয়া সমূহ এবং সেট সংক্রান্ত প্রশ্নাবলী খুব সহজেই বোঝা যায় ।
সাধারণত , একটি আয়তক্ষেত্রের বিন্দুসমূহ দ্বারা সার্বিক সেটের পদসমূহ সূচিত করা হয় এবং সার্বিক সেটের উপসেটকে ঐ আয়তক্ষেত্রের অন্তর্গত একটি বৃত্ত দ্বারা প্রকাশ করা হয় ।
(iii) দ্বিত নীতি – সেট সমূহের যোগ ( ∪ ) ও ছেদ ( ∩ ) প্রক্রিয়া দুটি দ্বিত নীতি মেনে চলে । এই নীতি অনুযায়ী যদি যোগ ও ছেদ প্রক্রিয়া দুটির কোনও একটি সম্পর্ক অভেদ হয় , তবে যোগের জায়গায় ছেদ ও ছেদের জায়গায় যোগ লিখে প্রাপ্ত দ্বৈত সম্পর্কটিও অভেদ হবে ।
উদাহরণস্বরূপঃ A ∪ ( B ∩ C ) = (A ∪ B ) ∩ (A ∪ C ) অভেদের দ্বৈত অভেদ হয় , A ∩ (B ∪ C ) = ( A ∩ B ) ∪ (A ∩ C )
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
সৌরেন্দ্রনাথ দে একাদশ শ্রেণির সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
6.যদি A= { a,b,c} হয় , তবে
(i) A এর উপসেট সমূহ এবং (ii) A এর যথার্থ উপসেট সমূহ লেখো ।
সমাধানঃ
(i)A এর উপসেট সমূহ Φ , {a},{b},{c}, {a,b},{b,c},{c,a},{a,b,c}
(ii) A এর যথার্থ উপসেট সমূহ Φ , {a},{b},{c}, {a,b},{b,c},{c,a}
SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
7. একটি সূচক সেটের সংজ্ঞা দাও । A = {{1},{2,3}} সেটের সূচক সেটটি লেখো ।
সমাধানঃ
A সেটের সূচক সেট P(A) = {Φ , {{1}}, {{2,3}}, A }
8. A ={1,2,3,4} , B = {2,4,5,8} ,C = {3,4,5,6,7} হলে (i) A U B (ii) B ∩ C
(iii) AU (BUC) (iv) AU (B ∩ C) নির্ণয় করো
সমাধানঃ
(i) AUB = {1,2,3,4,5,8}
(ii) B ∩ C = {4,5}
(iii) AU (BUC) = {1,2,3,4,5,6,7,8}
(iv) B ∩ C = {4,5}
∴ A U (B ∩ C) = {1,2,3,4,5 }
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
9. P = {a,b,c,d,e} এবং Q = {a ,e,i,o,u}হলে প্রমান করো যে (i) P ⊆ PUQ (ii) P ∩ Q ⊆ P
সমাধানঃ
(i) P U Q = {a,b,c,d,e,i,o,u}
∴ P ⊆ PUQ
(ii) P ∩ Q = {a,e}
∴ P ∩ Q ⊆ P
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
10. A ⊆ B এবং B ⊆ C হলেপ্রমানকরোযে A ⊆ C .
প্রমানঃ
ধরাযাক x ∈ A , x হল যেকোনো পদ ।
এখন x ∈ A ⇒ x ∈ B [ as A ⊆ B ]——-(i)
X ∈ B ⇒ x ∈ C [ as B ⊆ C ]——(ii)
(i) ও (ii) থেকে বলতে পারি A ⊆ C
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
11. A U B = B হলে দেখাওযে A ⊆ B ।
ধরাযাক , x ∈ A যে কোনও পদ ।
এখন x ∈ A ⇒ x ∈ (A ∪ B) ⇒ x ∈ B [ ∵ A ∪ B = B ]
x ∈ A ⇒ x ∈ B
∴ A ⊆ B
SN Dey Maths Class 11 Set Theory
12. A ⊆ B হলে দেখাও যে A –B = Φ
যেহেতু A ⊆ B ∴ x ∈ A ⇒ x ∈ B ,
সুতরাং A সেটে এমন কোনও পদ থাকবেনা যেটি B সেটে নেই ।
অর্থাৎ A –B = Φ
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
13. যেকোনো দুটি সেট A ও B এর ক্ষেত্রে , A ∪ B = A ∩ B হলে প্রমান করো যে A = B ।
সমাধানঃ
ধরি , x ∈ A , x যেকোনো একটি পদ ।
⇒ x ∈ A ∪ B
⇒ x ∊ A ∩ B [ As A ∪ B = A ∩ B ]
⇒ x ∈ A and x ∈ B
∴ A ⊆ B —— (i)
ধরি ,y ∈ B
∴ y ∈ A ∪ B
⇒ y ∈ A ∩ B
⇒ y ∈ A
∴ B ⊆ A —– (ii)
(i) ও (ii) থেকে বলতে পারি A = B
SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
14. (i) সেট প্রক্রিয়ার সাহায্যে প্রমান করো যে 3+4=7
সমাধানঃ
ধরাযাক A = {a,b,c} এবং B = { w,x,y,z}
স্পষ্টতই n(A) = 3 এবং n(B) = 4
আবার, A ∩ B = Φ
( A ∪ B ) = {a,b,c,w,x,y,z }
∴ n ( A ∪ B ) = 7
বা , n(A) +n(B) = 7 [ as n(A ∩ B ) = 0 ]
∴ 3 +4 = 7 ( প্রমানিত )
SN Dey Maths Class 11 Set Theory
14(ii) রসটার পদ্ধতিতে প্রকাশ করঃ
সমাধানঃ
A = {(x,y) : (x,y) হল y=x সরলরেখা এবং y = ex বক্রের ছেদবিন্দুর স্থানাঙ্ক }
যেহেতু y = x এবং y = e x সমীকরণ দ্বয়ের কোনও সাধারণ সমাধান নেই সুতরাং A = Φ ।
SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
সংক্ষিপ্ত উত্তরধর্মী ( প্রতিটি প্রশ্নের মান – 4 )
1. সংক্ষিপ্ত টীকা লেখোঃ
(i) সেট সমূহের ধারনা , উপসেট ,দুটি সেটের সমতা, সার্বিক সেট এবং শূন্য সেট , সসীম ও অসীম সেট ।
অনুচ্ছেদ 1.3 এবং 1.5 দেখো ।
(ii) দুটি সেটের যোগ ছেদ ও অন্তর ।
অনুচ্ছেদ 1.8 দেখো ।
(iii) সার্বিক সেট ও উপসেট
অনুচ্ছেদ 1.5 দেখো ।
(iv) তিনটি সেট প্রক্রিয়া ( যোগ , ছেদ এবং পূরকতা )
অনুচ্ছেদ 1.8 দেখো ।
2. ভেন চিত্র কি ? সেট তত্বের সাহায্যে এর গুরুত্ব ব্যাখ্যা করো ।
অনুচ্ছেদ 1.7 দেখো ।
3. সেটের বীজগাণিতিক সূত্রসমূহ বিবৃত করো ।
অনুচ্ছেদ 1.9 দেখো ।
4. দেখাও যে n সংখ্যক পদ বিশিষ্ট কোনও সসীম সেট A এর সূচক সেট 2n পদ বিশিষ্ট হবে ।
অনুচ্ছেদ 1.5 এর উপপাদ্য দেখো ।
5. মনে করো A = {a,b,c} , B = {a , b } ,C= {a ,b,d} , D = { c ,d} এবং E = {d}; যুক্তিসহ নিম্নলিখিত বক্তব্যগুলির মধ্যে কোনগুলি সত্য বলঃ
(i) B ⊂ A (ii) D ⊅ E (iii) D ⊂ B (iv) {a} ⊂ A
সমাধানঃ
(i) B ⊂ A
সত্য
কারণ B এর প্রত্যেকটি পদ A সেটেরও পদ
আবার B ≠ A কারণ c ∈ A কিন্তু c ∉ B
(ii) D ⊅ E
বিবৃতি টি মিথ্যা
কারণ E = { d } আবার D = { c ,d }
∴ E ⊂ D
∴ D ⊅ E সত্য নয় ।
(iii) D ⊂ B
স্পষ্টতই c ∈ D , d ∈ D কিন্তু c ∈ B এবং d ∈ B
∴ D ⊂ B সত্য নয় ।
(iv){a} ⊂ A
যেহেতু , a ∈ A সুতরাং {a} ⊂ A সত্য ।
SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
6. মনে করো A ={a,b,c,d,e,f,g,h,i} , B = {b ,d,f,h } C= {a,c,e,g,i}, D = { c,d,e} , এবং E ={ c,e }। যদি নিম্নলিখিত তথ্য দেওয়া থাকে তবে কোন সেট X এর সঙ্গে সমান হতে পারে ?
(i) X এবং B পরস্পর বিচ্ছেদ সেট
(ii) X ⊂ A কিন্তু X ⊄ C
(iii) X ⊂ D কিন্তু X ⊄ B
(iv) X ⊂ C কিন্তু X ⊄ A
সমাধানঃ
(i) X ও B পরস্পর বিচ্ছেদ সেট হবে যখন b,d,f,h ∉ X
সুতরাং X , C এবং E এর মধ্যে কোনও একটি হবে
∴ X = C or X = E
(ii) B ⊂ A and B ⊄ C
∴ X = B হতে পারে
আবার D ⊂ A এবং D ⊄ C
∴ X = D হতে পারে
(iii) স্পষ্টতই E ⊂ D এবং E ⊄ B
∴ X = E হতে পারে
(iv) যেহেতু B ,C ,D ,E প্রত্যেক টি সেটই A এর যথার্থ উপসেট হতে পারে সুতরাং B ,C ,D,E এর মধ্যে কোনটিই X হতে পারে না ।
এখন A ⊄ A [ যেহেতু A =A ]
কিন্তু A ⊂ C সত্য নয়
∴ X ≠ A
সুতরাং কোনও সেটই X এর সঙ্গে সমান হতে পারেনা ।
SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
7.A= {a,b,c,d,e } , B = {a ,c,e,g} এবং C = {b ,c,f,g} হলে দেখাও যে
(i) (A ∪ B) ∩ C = (A∩C) ∪ ( B∩C)
(ii) (A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C )
সমাধানঃ
(i) (A ∪ B) = {a,b,c,d,e} ∪ { a ,c,e,g }
= {a ,b,c,d,e,g}
∴ (A ∪ B) ∩ C = { a,b,c,d,e,g} ∩ {b,c,f,g }
= {b,c,g}
A ∩ C = {a,b,c,d,e }Ç{b ,c,f,g} = {b,c}
B ∩ C = {a ,c,e,g}Ç{b ,c,f,g} = {c , g }
∴ (A ∩ C) ∪ ( B ∩ C)
= {b,c}∪{c,g}
= {b,c,g}
∴ (A ∪ B) ∩ C = (A∩C) ∪ ( B∩C) [ প্রমানিত ]
(ii) (A∩B) = {a,b,c,d,e } ∩ {a ,c,e,g}
= { a , c,e}
∴ (A∩B)∪C
= {a ,c,e } ∪ {b ,c,f,g}
= {a,b,c,e,f,g}
A ∪ C
= {a,b,c,d,e } ∪ {b ,c,f,g}
={a,b,c,d,e,f,g}
B∪C
= {a,c,e,g} ∪ {b,c,f,g}
= {a,b,c,e,f,g}
∴ (A ∪ C) ∩ (B∪C )
= {a,b,c,d,e,f,g} ∩ {a,b,c,e,f,g}
= {a,b,c,e,f,g}
∴ (A∩B)∪C = (A ∪ C) ∩ (B ∪ C ) [প্রমানিত]
SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
8. (i) মনে করো সার্বিক সেট S = {1, 2, 3, 4, 5} এবং A = {3 , 4, 5} ও B = {1,4,5 }তার দুটি উপসেট । যাচাই করে দেখাও যে
( A ∪ B)’ = A’ ∩ B‘
সমাধানঃ
(i)A ∪ B = {3 , 4, 5} ∪ {1,4,5 }={1,3,4,5}
∴ ( A ∪ B)’ = S- (A ∪ B)
= {1,2,3,4,5} – {1,3,4,5}
= {2}
A’ = S –A ={1, 2, 3, 4, 5} – {3 , 4, 5} ={1,2}
B’ = S –B = {1, 2, 3, 4, 5}- {1,4,5} = {2,3}
A’ ∩ B’ = {2}
∴ ( A ∪ B)’ = A’ ∩ B’ [প্রমানিত ]
SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
8(ii) S = {1,2,3,4,5,6…12} – কে তিনটি সমউপাদান সংখ্যা বিশিষ্ট সেট A ,B,C তে বিভক্ত করা হল যাতে A ∪ B ∪ C = S , A ∩ B = B ∩ C = C ∩ A = Φ হয় । এরূপে S কে কত রকম বাবে বিভক্ত করা যাবে ?
সমাধানঃ
S এ মোট 12 টি পদ আছে ।
S সেটকে তিনটি সমউপাদান বিশিষ্ট সেট এ ভাগ করলে প্রতিটি সেট এ পদের সংখ্যা হবে 4 । প্রস্নানুসারে তিনটি সেটের প্রত্যেকটি পদ্গুলি ভিন্ন হবে এরূপে S সেট টিকে মোট 12!/(4! ✕4!✕ 4! ) = 12! / (4! )3 রকমভাবে বিভক্ত করা যাবে ।
9. A= {1,2,3,4} , B = {2,3,4,5} , C = {1,3,4,5,6,7} হলে (i) A-B (ii) A-C নির্ণয় করো:
অতঃপর দেখাও যে A – (B ∩ C) = (A-B) ∪ (A-C)
সমাধানঃ
(i) A –B = {1,2,3,4} – {2,3,4,5} = {1}
(ii) A-C = {1,2,3,4} – { 1,3,4,5,6,7} = {2}
∴ (A-B) ∪ (A-C ) = {1,2}
Now , B ∩ C = {3,4,5}
∴ A – (B ∩ C) = {1,2}
∴ A – (B ∩ C) = (A-B) ∪ (A-C) [ proved ]
SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
10. সার্বিক সেট S = {1,2,4,8,16,32} এবং A = {1,2,8,32} ও B = {4,8,32} তার দুটি উপসেট হলে দেখাও যে ,
(i) (Ac)c = A
(ii) (A ∩ B )c = Ac ∪ Bc
(iii) (A ∪ B)c = Ac ∩ Bc
সমাধানঃ
(i)A c
= S –A
={1,2,4,8,16,32} – {1,2,8,32}
= {4,16}
Now (Ac)c
= S – A c
= {1,2,4,8,16,32} – {4,16}
= {1,2,8,32}
=A
∴ (Ac ) c = A [ proved]
(ii) (A ∩ B )c = Ac ∪ Bc
A ∩ B = {1,2,8,32} ∩ {4,8,32}
= { 8 ,32 }
∴ (A ∩ B)c = S – (A ∩ B )
= {1,2,4,8,16,32} – {8,32}
= {1,2,4,16 }
A c
= S –A
={1,2,4,8,16,32} – {1,2,8,32}
= {4,16}
B c = S –B
= {1,2,4,8,16,32} – {4,8,32}
= {1,2 ,16}
Now, Ac ∪ Bc
= {1,2,4,16}
∴ (A ∩ B)c = A c ∪ B c [ Proved ]
(iii) (A ∪ B)c = Ac ∩ Bc
(A ∪ B )
= {1,2,4,8} ∪ {4 ,8,32}
= {1,2,4,8,32}
∴ (A∪B)c
= S – (A ∪ B )
= {1,2,4,8,16,32}- {1,2,4,8,32}
= {16}
Ac
= S –A
= {1,2,4,8,16,32}- {1,2,8,32}
= {4 ,16}
B c
= S – B
= {1,2,4,8,16,32}- {4,8,32}
= {1,2,16}
∴ Ac ∩ Bc
= {4,16} ∩ { 1,2,16}
= {16}
∴ (A ∪ B)c = Ac ∩ Bc [ proved ]
SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
11. (i) P = {a,b,c,d,e,f} এবং Q = {a,c,e,f } হলে প্রমান করো যে (P-Q ) ∪ (P ∩ Q) = P
(ii) যদি P = { ϴ : sinϴ -cosϴ = √2 cos ϴ}এবং Q = {ϴ : Sinϴ+cosϴ= √ sinϴ } হয় তবে দেখাও যে P = Q
সমাধানঃ
(i)P –Q = {a,b,c,d,e,f}- {a,c,e,f }
= {b,d}
P ∩ Q
= {a,b,c,d,e,f} ∩ {a,c,e,f }
= {a ,c,e,f}
∴ (P-Q) ∪ (P Ç Q)
= {b,d} ∪ {a,c,e,f}
= {a,c,e,f,b,d}
= P [ proved ]
(ii) ধরা যাক x ∈ P যেকোনো একটি পদ ।
∴ sinx-cosx = √2 cosx
⇒ sinx=(√2 +1) cosx
⇒ {1/(√2 +1)}sinx = cosx
⇒(√2-1)/(2-1)sinx = cosx[করণী নিরসন করে পাই ]
⇒ sinx+cosx=√2 sinx
⇒ x ∈ Q
∴ x ∈ P ⇒ x ∈ Q
∴ P ∈ Q ——- (i)
আবার y ∈ Q [ ধরা হল ]
∴ siny+cosy =√2 siny
⇒(√2-1) siny = cosy
⇒ siny = 1/(√2-1) cos y
⇒ siny = (√2 +1) cosy
⇒ siny –cosy = √2 cosy
⇒ y ∈ P
যেহেতু y একটি যেকোনো পদ সুতরাং Q ∈ P ——- (ii)
∴ (i) ও (ii) নং সমীকরণ থেকে পাই ,
P = Q [ প্রমানিত ]
SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
12. প্রদত্ত A = {1,2,3,4,5} এবং (B ∪ C)= {3,4,6}হলে
(i) (A ∩ B) ∪ (A ∩ C) (ii) (A – B) ∩ (A – C) নির্ণয় করো ।
সমাধানঃ
(i) (A ∩ B) ∪ (A ∩ C)
= A ∩ (B ∪ C )
= {1,2,3,4,5 } ∩ { 3,4,6}
= {3,4}
(ii) (A-B) ∩ (A-C)
= A- (B ∪ C)
= {1,2,3,4,5} – { 3,4,6}
= { 1,2,5}
SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
13. তিনটি সেট P ও Q এবং R এমনভাবে গঠন করা হল যাতে P ∩ Q ≠ Φ , Q ∩ R ≠ Φ , R ∩ P ≠ Φ কিন্তু P ∩ Q ∩ R = Φ হয় ।
সমাধানঃ ধরি P = {a,b } , Q = { b,c} এবং R = { c ,a }
∴ P ∩ Q = {b} ≠ Φ
Q ∩ R = {c} ≠ Φ
এবং (R ∩ P ) = {a} ≠ Φ
∴ P ∩ Q ∩ R = (P ∩ Q ) ∩ R = {b}∩{a,c } = Φ
SN Dey Maths Class 11 Set Theory
14. মনে করো A , B ,C তিনটি সেট । যদি A ⊂ B এবং B ⊂ C হয় তবে A ⊂ C হবে কি ? একটি উদাহরণের সাহায্যে তোমার উত্তরের সত্যতা প্রতিষ্ঠা করো ।
সমাধানঃ ধরাযাক x ∈ A , x হল যেকোনো পদ ।
এখন x ∈ A ⇒ x ∈ B [ as A ⊂ B ]——-(i)
X ∈ B ⇒ x ∈ C [ as B ⊂ C ]——(ii)
(i) ও (ii) থেকে বলতে পারি A ⊂ C
সুতরাং A ⊂ B , B ⊂ C হলে A ⊂ C হবে ।
SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
15. মনে করো সার্বিক সেট S = {a,b,c,d,e} এবং A = {a,b,d} ও B = {b,d,e} তার দুটি উপসেট । ( A ∩ B )c এবং (A ∪ B)c নির্ণয় করো ।
সমাধানঃ
A ∩ B = {a,b,d}∩ { b ,d,e} = {b,d}
(A ∩ B )c = S – ( A∩B ) = {a,b,c,d,e}-{b,d}= {a,c,e}
A ∪ B = {a,b,d} ∪ {b,d,e} = {a,b,d,e}
∴ (A ∪ B )c = S – ( A∪B) = {a,b,c,d,e}- {a,b,d,e}= {c}
SN Dey Maths Class 11 Set Theory
16.মনে করো সার্বিক সেট S = {1,2,3,4,5,6 } এবং A∪B = {2,3,4}; (Ac∩Bc ) নির্ণয় করো ।
সমাধানঃ
(Ac∩Bc )
= (A∪B)c
=S – (A∪B)
={1,2,3,4,5,6}-{2,3,4}
= {1,5,6}
SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
17. স্বাভাবিক সংখ্যা সমূহের সেট N এবং aN = {ax : x∈N} হলে , 3N ∩ 7N নির্ণয় করো ।
সমাধানঃ
aN = {ax:x∈N}
ধরা যাক , x∈ (3N ∩ 7N ), x যেকোনো পদ
⇒ x ∈ 3N এবং x∈7N
⇒ x = 3m এবং x = 7n , m,n ∈ N
x , 3 ও 7 উভয় দ্বারা বিভাজ্য
সুতরাং x ,3 ও 7 এর লসাগু দ্বারা বিভাজ্য।
∴ x=21p , p∈N
3N∩7N ⊆ 21N —— (i)
আবার,21N⊆3N এবং 21N⊆7N
[ ∵21k=3(7k) =7(3k),7k,3k∈N যখন k ∈N ]
21N ⊆ 3N∩7N——-(ii)
(i) ও (ii) থেকে পাই ,
3N∩7N=21N
Another Method
3N={3,6,9,12,15,18,21,24,………}
7N= {7,14,21,28,35,42,49,………}
3N∩7N = {21,42,……..}=21N
SN Dey Maths Class 11 Set Theory
18. মনে করো সব অখণ্ড সংখ্যার সেট Z এবং A={x:x=6n,n∈Z} ও B={x:x=4n,n∈Z}; A∩B নির্ণয় করো ।
সমাধানঃ
A={x:x=6n,n∈Z}=6N
B ={x:x=4n ,n∈Z } =4N
A∩B = 6N∩4N=12N ={x:x=12n,n∈Z}
SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
19.যেকোনো সেট A ও B এর ক্ষেত্রে নিম্নলিখিত গুলি প্রমান করঃ
(i)(B-A)∩A=Φ
(ii)Ac-Bc=B-A
(iii)A-B=A-(A∩B)
(iv)A-B=A∩Bc
(v) B-Ac=A∩B
(vi) B⊆(A-B)c
(vii)(A∪B)-(A∩B)=(A-B)∪(B-A)
(viii) (A-B)∪(A∩B)=A
সমাধানঃ
(i) A ও B দুটি সেটের মধ্যে দুটি সেটই যদি শূন্য হয় তবে স্পষ্টতই A∩(B-A)= Φ হবে ।
যখন A ও B দুটি সেটের কোনও সেট শূন্য না হলে ধরা যাক A∩(B-A)≠ Φ
তাহলে A∩(B-A) সেটে কমপক্ষে একটি পদ থাকবে । যদি ঐ পদটি x হয় তবে,
x ∈ A∩(B-A)
⇒x∈A and x∈(B-A)
⇒x∈A and (x∈B and x∉A)
(x∈A and x∉A)and x∈B
কিন্তু (x∈A and x∉A) এটি অসম্ভব
অর্থাৎ আমাদের কল্পনা সত্য নয় ।
সুতরাং A∩(B-A)= Φ [ প্রমানিত ]
(ii) ধরাযাক , x ∈ Ac-Bc , x যেকোনো একটি পদ
x ∈ Ac-Bc
⇒ x∈Ac and x∉Bc
⇒ x∉A and x∈B
⇒x∈B and x∉A
⇒ x∈(B-A)
Ac-Bc ⊆ (B-A)—–(i)
ধরাযাক y ∈ B-A, y যেকোনো পদ
⇒y ∈ B-A
⇒y∈B এবং y∉A
⇒y∉Bc এবং y∈Ac
⇒y∈Acএবং y∉Bc
⇒y∈Ac-Bc
∴B-A ⊆ Ac-Bc ——-(ii)
(i) ও (ii) থেকে বলতে পারি Ac-Bc=B-A
(iii) দুটি সেট A ও B এর জন্য , A∩B⊆B
ধরাযাক , x∈(A-B)
⇒ x∈A and x∉B
⇒x∈A and x∉A∩B [ ∵A∩B⊆B ]
⇒x ∈A-(A∩B)
∴ x∈(A-B)⇒x ∈A-(A∩B)
∴(A-B)⊆A-(A∩B)—— (i)
এখন ধরাযাক, y∈ A-(A∩B), y হল যে কোনও পদ
y∈ A-(A∩B)
y∈A and y∉(A∩B)
⇒ y∈A and (y∉A or y∉B)
⇒(y∈A and y∉A)or(y∈A and y∉B)
⇒(y∈A and y∈Ac )or(y∈A and y∉B )
⇒y∈(A∩Ac ) or y∈(A-B)
⇒y∈{(A∩Ac ) ∪(A-B)}
⇒y∈ Φ∪(A-B)
⇒y∈(A-B)
সুতরাং, y∈ A-(A∩B)⇒y∈(A-B)
A-(A∩B)⊆(A-B)——– (ii)
(i) ও (ii) থেকে পাই ,
A-(A∩B) = (A-B) [ proved ]
(iv)ধরা যাক x∈(A –B) ,x যেকোনো একটি পদ
x ∈ A-B
⇒ x∈A and x∉B
⇒x ∈ A and x ∈ B’
⇒ x ∈ A∩B’
∴ x ∈(A-B) ⇒ x∈ (A ∩ B’)
∴ A-B ⊆ A∩B’——-(i)
ধরাযাক, y ∈ A∩B’
∴ y ∈ A and y ∈ B’
⇒ y ∈ A and y ∉ B
⇒ y∈ A-B
∴ y ∈ A∩B’ ⇒y ∈ A-B
∴ A ∩ Bc ⊆ A-B—–(ii)
So from (i) and (ii)
A-B = A∩Bc [ proved ]
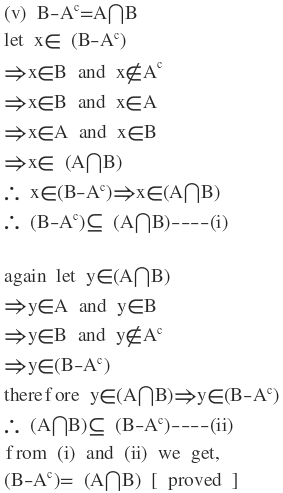



SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
20.মনে করো , A, B এবং C তিনটি প্রদত্ত সেট, উদাহরণের সাহায্যে প্রমান করো যে , নীচের বিবৃতি গুলো সত্য নয়ঃ
(i) B∈A এবং x∈B হলে x∈A হবে ।
(ii) B⊂A এবং A∈C হলে ,B∈C হবে
(iii) A⊄ B এবং B⊄C হলে , A⊄C হবে
সমাধানঃ
(i) ধরাযাক B ={x} এবং A = {{x}}=B
স্পষ্টতই x∈B এবং B∈A
কিন্তু, x∈A
সুতরাং প্রদত্ত বিবৃতিটি সত্য নয় ।
(iii) ধরাযাক , A ={x} এবং B ={y,z}, C ={x,z}
স্পষ্টতই , A⊄B এবং B⊄C
কিন্তু, A⊂C
সুতরাং প্রদত্ত বিবৃতি টি সত্য নয় ।
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
21. সেট প্রক্রিয়ার সাহায্যে 12,15,এবং 18 সংখ্যা তিনটির গসাগু নির্ণয় করো ।
সমাধানঃ
ধরাযাক A ,B ও C যথাক্রমে 12,15,18 সংখ্যা তিনটির উৎপাদক সমূহের সেট ।
∴ A = {1,2,3,4,6,12}
B = {1,3,5,15}
C= {1,2,3,6,9,18}
এখন, A∩B∩C={1,3}
স্পষ্টতই A∩B∩C সেটের অন্তর্গত পদসমূহের মধ্যে বৃহত্তম পদটির মান প্রদত্ত সংখ্যা তিনটির গসাগু হবে । সুতরাং , প্রদত্ত সংখ্যা তিনটির গসাগু 3 ।
SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
23.ভেন চিত্রের প্রয়োগে আব অন্য পদ্ধতিতে নীচের প্রস্নতির সমাধান করোঃ
একটি স্রেনিতে 70 জন ছাত্র আছে যাদের প্রত্যেকের হয় ইংরাজি বা হিন্দি বা উভয় বিষয় পাঠ করে । 45 জন ছাত্র ইংরাজি এবং 30 জন ছাত্র হিন্দি পাঠ করে । কতজন ছাত্র উভয় বিষয় পাঠ করে তা নির্ণয় করো ।
সমাধানঃ
ধরাযাক, ইংরাজি এবং হিন্দি পাঠ করে এমন ছাত্রদের সেট যথাক্রমে E ও H ।
প্রশ্নানুসারে, n(E) = 45, n(H)= 30
70 জন ছাত্র হয় ইংরাজি বা হিন্দি বা উভয় বিষয় পাঠ করে।
∴ n(E ∪ H) =70
Implies n(E) +n(H)-n(E∩H)=70
Implies 45+30-n(E∩H)=70
∴ n(E∩H) = 5
সুতরাং উভয় বিষয় পাঠ করে এমন ছাত্রের সংখ্যা 5 জন ।
SN Dey Maths Class 11 Set Theory
24. কলকাতার 1003 টি পরিবারের তথ্য অনুসন্ধানে দেখা গেল 63 টি পরিবারের রেডিও বা টিভি ছিলনা;794 টি পরিবারের রেডিও এবং 187 টি পরিবারে টিভি ছিল । কতগুলো পরিবারের রেডিও এবং টিভি উভয় ছিল ?
সমাধানঃ
ধরাযাক রেডিও টিভি ছিল এমন পরিবার সমূহের সেট যথাক্রমে R এবং T ।
প্রদত্ত, n (R)= 794 , n (T)= 187
∴রেডিও বা টিভি ছিলনা এমন পরিবার সমূহের সেট = (R∪T)c
প্রশ্নানুযায়ী, n(R∪T)c =63
⇒ U – n(R∪T) = 63
⇒1003 – n(R∪T) = 63
⇒N(R∪T) = 1003-63
⇒ n (R∪T) =940
⇒ n(R) + n(T) – n(R ∩ T) = 940
⇒794 +187 – n(R ∩ T)=940
⇒ n(R ∩ T) = 940-794-187
⇒n(R∩T) = 41
সুতরাং , রেডিও , টিভি উভয় ছিল এম পরিবারের সংখ্যা 41 ।
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
25. কোনও বাজার অনুসন্ধানকারী দল 1000 জন ব্যবহারকারীর তথ্য অনুসন্ধান করল এবং রিপোর্ট করল যে, 720 জন ব্যবহারকারী A সামগ্রী এবং 450 জন ব্যবহারকারী B সামগ্রী পছন্দ করে । কমপক্ষে কতজন উভয় সামগ্রী পছন্দ করে ?
সমাধানঃ
ধরাযাক , A ও B সামগ্রী ব্যবহারকারী দের সেট যথাক্রমে X এবং Y ।
প্রশ্নানুযাই, n(X) =720 , n(Y) = 450 ।
এখন , n(X∪Y)= 1000
⇒ n(X)+n(Y)-n(X∩Y)= 1000
⇒720+450-n(X∩Y) =1000
⇒1170- n(X∩Y) = 10000
⇒n(X∩Y) = 1170-1000
⇒ n(X∩Y)= 170
সুতরাং , 170 জন উভয় সামগ্রী পছন্দ করে ।
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
26. কোনও শহরে শতকরা 60 জন A পত্রিকা পাঠ করে এবং শতকরা 25 জন A পত্রিকা পাঠ করেনা কিন্তু B পত্রিকা পাঠ করে । শতকরা কতজন কোনও পত্রিকা পাঠ করে না তা গণনা করো । সম্ভাব্য সর্বাধিক ও সর্বনিম্ন কতজন B পত্রিকা পাঠ করে তাও নির্ণয় করো ।
সমাধানঃ
ধরাযাক A ও B পত্রিকা পাঠ করে এমন ব্যাক্তির সংখ্যার সেট যথাক্রমে X ও Y ।
প্রদত্ত শর্তানুসারে , n(X)=60 এবং n(Y∩X’)=25
কোনও না কোনও পত্রিকা পাঠ করে এমন ব্যাক্তির শতকরা সংখ্যা
n(X∪Y) = n(X) +n(Y∩X’)
=60+25
=85
সুতরাং কোনও পত্রিকাই পাঠ করে না এমন ব্যাক্তির শতকরা সংখ্যা = 100-85 =15
আবার Y ⊆ (X∪Y)
Implies n(Y)≤n(X∪Y)
Implies n(Y) ≤ 85
সুতরাং সম্ভাব্য সর্বাধিক শতকরা 85 জন B পত্রিকা পাঠ করে ।
আবার , n(X ∩ Y ) ≥ 0
⇒ n(X) +n(Y) – n(XUY)≥ 0
⇒ 60 +n(Y) -85 ≥ 0
⇒ n(Y) ≥ 25
সুতরাং সম্ভাব্য সর্বনিম্ন শতকরা 25 জন B পত্রিকা পাঠ করে ।
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
27.(i)দুটি সেট A ও B এর পদ সংখ্যা যথাক্রমে p ও q ; যদি A সেটের উপসেটের সংখ্যা , B সেটের উপসেটের সংখ্যার চেয়ে 56 বেশি হয় , তবে p ও q এর মান নির্ণয় করো ।
27(ii). দুটি সসীম সেট A এবং B এর উপাদান সংখ্যা যথাক্রমে m এবং n হলে ,A∪B – এর সবচেয়ে বেশি এবং সবচেয়ে কম কতগুলি উপাদান সংখ্যা পাওয়া যাবে ।
সমাধানঃ
(i)প্রদত্ত A সেটের পদসংখ্যা , n(A) = p এবং B সেটের পদসংখ্যা , n(B)= q ।
এখন A সেটের উপসেটের সংখ্যা = n(P(A))=2p
এখন B সেটের উপসেটের সংখ্যা = n(P(B)) = 2 q
প্রশ্নানুসারে , 2p =2q +56
⇒ 2q (2 p-q -1) = 56 = 23 (23-1)
স্পষ্টতই , উপরক্ত শর্ত সিদ্ধ হয় যখন q =3 , p-q = 3 অর্থাৎ p=6 ,q =3 হবে ।
(ii) আমারা জানি ,
N(AUB) = n(A)+n(B)-n(A∩B)
= m+n-n(A∩B)
আমরা জানি , Φ ⊆ A∩B⊆ A এবং Φ ⊆ A∩B ⊆ B
n(Φ) ≤ n(A∩B) ≤ n(A)
এবং n(Φ)≤ n(A∩B)≤ n(B)
∴ 0≤ n(A∩B) ≤ m —– (i)
এবং 0≤ n(A∩B) ≤ n —– (ii)
(i) ও (ii) থেকে পাই ,
0 ≤ n(A∩B) ≤ min{m,n} = m , যখন m less or equal n
n , যখন n ≤ m
⇒ – min{m,n} ≤ –n (A∩B) ≤ 0
⇒ m+n-min{m,n}≤ m+n-n(A∩B)≤ m+n
⇒ m+n-min{m,n} ≤ n(A∪B) ≤ m+n
সুতরাং n(AUB) এর সর্বচ্চ ও সর্বনিম্ন মান যথাক্রমে m+n ও m+n-min{m,n} ।
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
দীর্ঘ উত্তরধর্মী ( প্রতিটি প্রশ্নের মান – 5)
1. দুটি সসীম সেট A এর ক্ষেত্রে , A সেটের পদসংখ্যা n(A) দ্বারা প্রকাশ করা হয় । একটি ভেন চিত্রের প্রয়োগে বা অন্য কোনও পদ্ধতিতে যেকোনো দুটি সেট A ও B এর ক্ষেত্রে প্রমান করো যে , N(AUB)=n(A)+n(B)-n(A∩B)
তিনটি সেট A , B ,C এর ক্ষেত্রে এই ফল বিস্তৃত করো ।
প্রমানঃ মনে করো A , B এবং (A∩B) সেট তিনটির পদ সংখ্যা যথাক্রমে p ,q এবং r ; অর্থাৎ
N(A)=p , n(B)=q , n(A∩B) = r ।
এখন ভেন চিত্র থেকে সহজেই বোঝা যায় যে ,
N(A-B) = n(A)-n(A∩B) = p-r
N(B-A) = n(B)- n(A∩B) = q-r
আবার ভেন চিত্র থেকে আরও বোঝা যায় যে , (A-B) , (AÇB) এবং (B-A) সেট তিনটি পরস্পর বিচ্ছেদ সেট (disjoint set ) এবং (A∪B) পদের পদসংখ্যা =(A-B) , (A∩B) এবং (B-A) এই সেট তিনটির পদের সমষ্টির সমান ।
অর্থাৎ , n(A∪B) = n(A-B) +n(A∩B) +n(B-A)
বা, n(A∪B) = p-r+r+q-r = p+q-r
∴ n(A∪B) = n(A) +n(B)- n(A∩B) [ proved ]
এবার প্রমান করতে হবে ,

SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
SN Dey Class 11 Semester -1 সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
2. A={0<x ≤ 2} এবং B = {x:1<x<3} হলে
(i) A ∩ B
(ii) A ∪ B
(iii) A-B
(iv) (AUB)- (A∩B)
নির্ণয় করো ।
সমাধানঃ
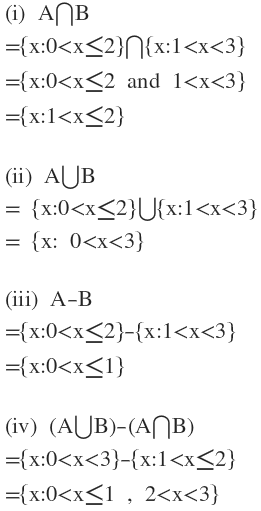
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
3.A = {2≤x<5} এবং B= {x: 3<x<7} হল সার্বিক সেট ,S={x: 0<x≤10} এর দুটি উপসেট
প্রমান করো যে , (A union B )c = Ac intersection Bc
সমাধানঃ
A∪B = {x:2≤x<7}
(AUB)c
=S-(AUB)
={x:0<x ≤10}-{x: 2≤x<7}
= {x: 0<x <2, 7≤x≤10 }
এখন,
Ac = {x:0< x <2, 5≤x≤10 }
এবং Bc = {x: 0 <x ≤3, 7≤x≤10 }
∴ Ac ∩ Bc = {x: 0<x< 2, 7≤x≤10 }
∴ (A ∪ B)c = Ac ∩ Bc [ proved ]
SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
সৌরেন্দ্রনাথ দে একাদশ শ্রেণির সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
4.P ={p,q,r,s,t,u} এবং Q intersection R={q,r,v,w} হলে ,
(i) (P U Q)∩(PUR) (ii)(P-Q)U(P-R) নির্ণয় করো ।
সমাধানঃ
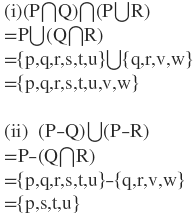
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
5.যদি S সার্বিক সেটের A , B ,C তিনটি উপসেট হয় , যেখানে S ={1,2,3,4,5,6,7} , A={1,3,5,6}, B∩C={1,2,6},
তবে (A ∪ B)∩ (A∪ C) এবং (Bc ∩ Cc ) নির্ণয় করো ।
সমাধানঃ
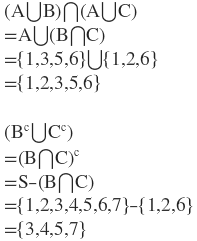
SN Dey Maths Class 11 Set Theory
6.যদি U = {a,b,c,d,e,f} সার্বিক সেট হয় এবং A,B,C যদি U এর তিনটি উপসেট হয় , যেখানে A = {a,c,d} এবং (B∪C) ={a,d,c,f}, তবে (A∩B)∪(A∩C) এবং (Bc∩Cc ) নির্ণয় করো ।
সমাধানঃ
(A∩B)U(A∩C)= A∩(B U C)={a,c,d}
(Bc∩Cc)= (BUC)c= U-(BUC)={b,e}
SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
7. প্রদত্ত X∪Y ={1,2,3,4} , X ∪ Z={2,3,4,5}, X ∩ Y ={2,3} এবং X∩Z ={2,4}; X ,Y ,Z এর মান নির্ণয় করো ।
সমাধানঃ
| element \Set | Set X | Set Y | Set Z |
| 1 | ✖ [∵1 ∉XUZ ] | ✔ [∵1∈ (X∪Y) এবং 1∉(X∪Z)] | ✖ [∵1∉ (X∪Z)] |
| 2 | ✔ [∵ 2∈(X∩Y)] | ✔ [∵ 2∈(X∩Y)] | ✔ [∵ 2∈(X∩Z)] |
| 3 | ✔ [∵ 3∈(X∩Y)] | ✔ [∵ 3∈(X∩Y)] | ✖ [∵3∈X এবং 3∉(X∩Z)] |
| 4 | ✔ [∵4∈(X∩Z)] | ✖ [∵4∈X এবং 4∉(X∩Y)] | ✔ [∵4∈(X∩Z)] |
| 5 | ✖ [∵5∉(X∪Y)] | ✖ [∵5∉(X∪Y)] | ✔ [∵5∈(X∪Z) এবং5∉(X∪Y)] |
∴ X={2,3,4} ,Y={1,2,3}, Z={2,4,5}
SN Dey Maths Class 11 Set Theory
10.যেকোনো তিনটি সেট A,B,C এর ক্ষেত্রে নিম্নলিখিত গুলি প্রমান করোঃ
(i) A∪(B∩C) = (A∪B)∩(A∪C)
সমাধানঃ

SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
(ii)A∩(B∪C)=(A∩B)∪(A∩C)
সমাধানঃ

SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
(iii)A∪(B∪C)=(A∪B)∪C
সমাধানঃ

(iv)A∩(B∩C)=(A∩B)∩C
সমাধানঃ
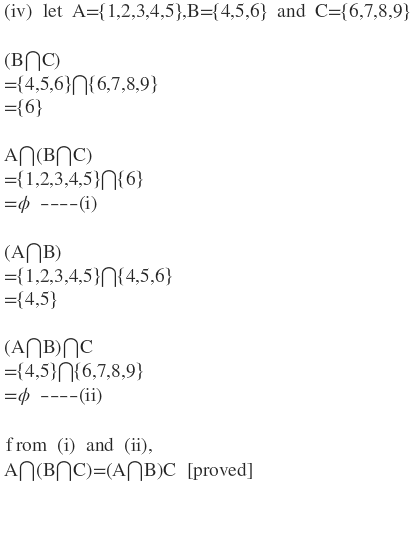
(v)(A∪B)c =Ac∩Bc
সমাধানঃ

SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
(vi)(A∩B)c = Ac ∪ Bc
সমাধানঃ

SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
SN Dey Class 11 Semester -1 সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
(vii)A-(B∪C)=(A-B)∩(A-C)
সমাধানঃ

SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
(viii)A-(B∩C)=(A-B)∪(A-C)
সমাধানঃ

SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
(ix)(A-C)∩(B-C)=(A∩B)-C
সমাধানঃ

SN Dey Maths Class 11 Set Theory|SN Dey Math Solution Of Set Theory Of Class 11|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
(x)(A∪B)-C=(A-C)∪(B-C)
সমাধানঃ

SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
11. সেট বীজগণিতের সূত্রাবলী প্রয়োগে নিম্নলিখিতগুলি প্রমান করো ঃ
(i) A∩(B-A)=Φ
সমাধানঃ
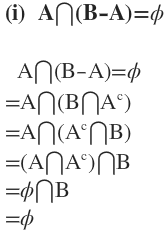
(ii) A∪(B-A)=A∪B
সমাধানঃ
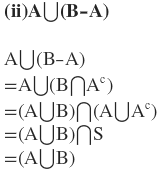
SN Dey Class 11 Semester -1 সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
(iii) (A∩B)-C =(A-C)∩(B-C)
সমাধানঃ
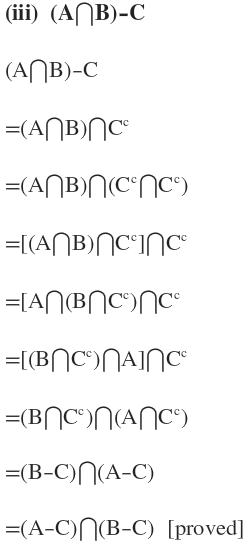
(iv)(A∪B)-C=(A-C)∪(B-C)
সমাধানঃ
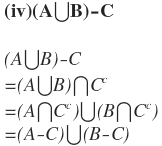
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
12.কোনও engineering college-এ 80 জন ছাত্র computer science , 75 জন information technology এবং 72 জন electronics-এ পড়ার সুযোগ পায় ; যদি 60 জন ছাত্র প্রথম ও দ্বিতীয় ,50 জন ছাত্র দ্বিতীয় ও তৃতীয় এবং 40জন প্রথম ও তৃতীয় এবং 30 জন তিনটি শাখাতেই পড়ার সুযোগ পেয়ে থাকে তবে কলেজে ছাত্রদের জন্য কতগুলো আসন আছে ? ( ধরে নাও কলেজে কেবল তিনটি শাখাই আছে )
সমাধানঃ
ধরা যাক , Computer science , Information Technology ও Electronics এর ছাত্রদের সেট যথাক্রমে A,B এবং C
এখন,
n(A)=80
n(B)=75
n(C)= 72
n(A∩B)=60
n(B ∩ C)=50
n(C ∩ A)=40
এবং n(A∩B∩C )=30
কলেজের মোট ছাত্রসংখ্যা অর্থাৎ n(AUBUC) নির্ণয় করতে হবে
∴ n(AUBUC)
=n(A)+n(B)+n(C)-n(A∩B)-n(B∩C)-n(C∩A)+n(A∩B∩C)
=80+75+72-60-40-50+30
= 107
অর্থাৎ কলেজে ছাত্রদের দের জন্য মোট আসন সংখ্যা 107টি ।
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
13.100 জন ছাত্রের তথ্যুানুসন্ধানে দেখা গেল 50জন ছাত্র কলেজ লাইব্রেরীর পুস্তক ব্যাবহার করত , 40 জনের নিজস্ব পুস্তক ছিল এবং 30 জন ধার করা পুস্তক ব্যাবহার করত ; 20 জন লাইব্রেরীর পুস্তক ব্যাবহার করত এবং তাদের নিজস্ব পুস্তক ও ছিল , 15 জন নিজস্ব পুস্তক এবং ধারকরা পুস্তক ও ব্যাবহার করত এবং 10 জন কলেজ লাইব্রেরীর পুস্তক ও ধার করা পুস্তক ব্যাবহার করত । প্রত্যেক ছাত্র কলেজ লাইব্রেরীর পুস্তক অতঝবা নিজস্ব পুস্তক অথবা ধারকরা পুস্তক ব্যাবহার করে ধরে তিনটি উৎস থেকেই পুস্তক ব্যবহার করত এমন ছাত্র সংখ্যা নির্ণয় করো ।
সমাধানঃ
ধরাযাক , সমগ্র ছাত্রের সেট S , লাইব্রেরীর পুস্তক ব্যাবহারকারী ছাত্রের সেট =A, নিজস্ব পুস্তক ব্যাবহারকারী ছাত্রের সংখ্যা = B এবং ধারকরা পুস্তক ব্যাবহারকারী ছাত্রের সেট = C
এক্ষেত্রে ,
n(S)=n(AUBUC)=100
n(A)=50
n(B)= 40
n(C )= 30
n(A∩B)= 20
n(B∩C) = 15
n(C∩A)= 10
n(A∩B∩C) নির্ণয় করতে হবে
n(AUBUC)=n(A)+n(B)+n(C)-n(A∩B)-n(B∩C)-n(C∩A)-n(A∩B∩C)
⇒100=50+40+30-20-15-10+n(A∩B∩C)
⇒100=75+n(A∩B∩C)
⇒n(A∩B∩C)= 100-75
⇒n(A∩B∩C) = 25
অর্থাৎ তিনটি উৎস থেকেই পুস্তক ব্যাবহার করে এমন ছাত্র সংখ্যা 25 জন ।
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
সৌরেন্দ্রনাথ দে একাদশ শ্রেণির সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
14.কোনও কম্পানি 300 জন ব্যাবহারকারীর কোন ধরনের সামগ্রী পছন্দ করেন তার অনুসন্ধান করে । দেখা গেল যে, 226 জন A সামগ্রী , 51 জন B সামগ্রী , 54 জন C সামগ্রী , 21 জন A ও B উভয় সামগ্রী , 54 জন A ও C উভয় সামগ্রী , 39 জন B ও C উভয় সামগ্রী এবং 9 জন তিন ধরনের সামগ্রী পছন্দ করেন ।প্রমান করো যে তথ্যানুসন্ধানের ফলসমূহ সঠিক নয় (ধরে নাও যে প্রত্যেক ব্যাবহার কারী অন্তত একধরনের সামগ্রী পছন্দ করেন ) ।
সমাধানঃ
A সামগ্রী,B সামগ্রী এবং C সামগ্রী ব্যাবহার কারীর সেট যথাক্রমে X ,Y এবং Z ধরা হল ।
∴ n(X)=226
n(Y)= 51
n(Z)=51
n(X ∩ Y)= 21
n(X ∩ Z )=54
n(Y ∩ Z)=39
and n(X ∩ Y ∩ Z )= 9
মোট ব্যাবহারকারীর সংখ্যা = (X ∪ Y ∪ Z) নির্ণয় করতে হবে ।
n(X∪Y∪Z) = n(X) +n(Y) +n(Z) – n(X∩Y)-n(Y∩Z)-n(Z∩X)+n(X∩Y∩Z)
= 226+51+54-21-39-54+9
= 226
প্রশ্নানুযায়ী , মোট ব্যাবহার কারীর সংখ্যা 300 অর্থাৎ তথ্যানুসন্ধানের ফলসমূহ সঠিক নয় ।
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
15. শ্রমিকদের দ্বারা উৎপাদিত 100 টি সামগ্রী পরীক্ষা করে সেন ,সরকার ও লাহিড়ী কোম্পানিরম্যানেজার তাঁর বসের কাছে নিম্নলিখিত রিপোর্ট দাখিল করেনঃ
পরিমাপে ত্রুটি 50 টি সামগ্রীতে , রঙে ত্রুটি 30 টিতে , উৎকর্ষে ত্রুটি 23 টিতে , উৎকর্ষে ও রঙে ত্রুটি 10 টিতে , পরিমাপ ও রঙে ত্রুটি 8 টিতে, পরিমাপ ও উৎকর্ষে ত্রুটি 20 টিতে এবং 5 টি সবগুলোতেই ত্রুটিপূর্ণ । দাখিল করা রিপোর্টটির জন্য ম্যানেজার কে দণ্ড দেওয়া হল । সেট তত্ত্বের প্রয়োগে দণ্ড দেওয়ার কারণ ব্যাখ্যা করো ।
সমাধানঃ
ধরাযাক A ,B ,C দ্বারা যথাক্রমে পরিমাপে ত্রুটি , রঙে ত্রুটি ও উৎকর্ষে ত্রুটি রয়েছে এমন সামগ্রীর সেট নির্দেশিত হয় ।
∴ n(A)= 50
n(B) = 30
n(C) = 23
n(A ∩ B)=8
n(B ∩ C)= 10
n(A ∩ C)= 20
n (A ∩ B ∩ C)=5
∴ মোট সামগ্রী সংখ্যা নির্দেশিত সেটটি হল ( A∪B∪C)
n(A∪B∪C)=n(A)+n(B)+n(C)-n(A∩B)-n(B∩C)-n(C∩A)+n(A∩B∩C)
=50+30+23-8-10-20+5
=103-38+5
=103-33
=70
∴ মোট সামগ্রী সংখ্যা = 70
কিন্তু প্রদত্ত শর্তানুসারে মোট সামগ্রী সংখ্যা = 100 যা অসম্ভব । তাই দাখিল করা রিপোর্টটির জন্য ম্যানেজার কে দণ্ড দেওয়া হল ।
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
SN Dey Class 11 Semester -1 সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
16.কোনও শহরে সংবাদ পত্র X,Y,Z প্রকাশিত হয় । ঐ শহরে 65% লোক X পত্রিকা, 54% লোক Y পত্রিকা ,45% লোক Z পত্রিকা পড়ে ; 38% লোক X ও Y ; 32% লোক Y ও Z ; 28% লোক X ও Z পত্রিকা পড়ে এবং 12% লোক ঐ তিনপ্রকার পত্রিকার কোনটাই পড়ে না । যদি শহরে মোট লোক সংখ্যা 1000000 জন হয় তবে শহরে কতজন লোক 3টি পত্রিকাই পড়ে তা নির্ণয় করো ।
সমাধানঃ
ধরি মোট পাঠকের সংখ্যা = 100 টি ।
∴ n(U)= 100
ধরাযাক X ,Y ,Z সংবাদপত্রের পাঠকের সেট যথাক্রমে A ,B এবং C
শর্তানুসারে,
n(A)= 65
n(B)=54
n(C)= 45
n(A∩B) = 38
n(B∩C) = 32
n(C∩A ) = 28
n( Ac∩Bc∩Cc ) =12
এখন তিনটে সংবাদপত্রই পড়ে এমন পাঠকের সংখ্যা =n(A∩B∩C )
n(Ac∩Bc∩Cc )=n(A U B U C)c
⇒ n(Ac ∩ Bc ∩ Cc )=n(U) – n(A∪B∪C)
⇒ 12 = 100-n(A∪B∪C)
⇒ n(A∪B∪C)= 100-12
⇒ n(A∪B∪C)= 88
⇒n(A)+n(B)+n(C) –n(A∩B)-n(B∩C)-n(A∩C) +n(A∩B∩C) =88
⇒ 65 +54+45 – 38-32-28 +n(A ∩ B ∩ C) =88
⇒ 66+n(A ∩ B ∩ C) = 88
⇒ n( A∩B∩C) = 88-66
⇒ n(A ∩ B ∩ C ) = 22
100 জন মোট পাঠক সংখ্যা হলে তিনটে পত্রিকাই পড়ে এমন পাঠকের সংখ্যা 22 জন
∴ 1000000
জন মোট পাঠক হলে তিনটে পত্রিকাই পড়ে এমন পাঠকের সংখ্যা
= 22/100 ✕ 1000000
= 220000 জন
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
17.কোনও কলেজের 1000 জন ছাত্রের মধ্যে 540 জন ফুটবল ,465 জন ক্রিকেট এবং 370 জন ভলিবল খেলে ; মোট ছাত্র সংখ্যার 325 জন ফুটবল ও ক্রিকেট ,260 জন ফুটবল ও ভলিবল ,235 জন ক্রিকেট ও ভলিবল এবং 125 জন প্রত্যেকটি গেম খেলে । কতজন ছাত্র
(i) কোনও গেম খেলে না?
(ii) কেবল একটি গেম খেলে
(iii) ঠিক দুটো গেম খেলে ?
সমাধানঃ ধরাযাক , ক্রিকেট , ফুটবল ও ভলিবল খেলা ছাত্রের সেট যথাক্রমে A,B এবং C । কলেজের মোট ছাত্রের সেট = U
শর্তানুসারে ,
n(U)=1000
n(A)= 465
n(B) = 540
n(C ) = 370
n(A ∩ B)= 325
n(B ∩ C )=260
n(C ∩ A )= 235
n(A ∩ B ∩ C ) = 125
এখন , n( A U B U C )
= n(A)+n(B)+n(C)-n(A∩B)-n(B∩C)-n(C∩A )+n(A ∩ B ∩ C )
=465+540+370-325-260-235+125
=680
(i) কোনও গেম খেলে না এমন ছাত্রের সংখ্যা
= n( Ac ∩ Bc ∩ Cc)
= n (A ∩ B ∩ C)c
= n(U)-n(A ∪ B ∪ C )
= 1000-680
= 320
(ii)
শুধু ক্রিকেট খেলে এমন ছাত্রের সংখ্যা ,
= n(A∩ Bc ∩Cc)
= n(A)-n(A ∩ B)-n(A ∩ C)+n( A∩B∩C)
= 465-325-235+125
=30
শুধু ফুটবল খেলে এমন ছাত্রের সংখ্যা ,
n(B∩ Ac ∩ Cc)
= n(B)-n(A ∩ B)-n(B ∩ C)+n(A∩B∩C)
= 540-325-260+125
=80
শুধু ভলিবল খেলে এমন ছাত্রের সংখ্যা,
n(C ∩ Ac ∩ Bc)
= n( C )-n(A∩C)-n(B∩C)+n(A∩B∩C )
= 370-235-260 +125
= 0
∴ কেবল একটিই গেম খেলে এমন ছাত্রের সংখ্যা ,
n(A∩Bc∩Cc)+ n(B ∩ Ac ∩ Cc)+ n(C∩Ac∩Bc)
= 80+30+0
= 110
(iii) ঠিক দুটো গেম খেলে এমন ছাত্রের সংখ্যা ,
n(A∩B∩Cc)+n(A∩Bc ∩ C) +n(Ac ∩ B ∩ C)
={n(A∩B )-n (A ∩ B ∩ C)}+{n(A ∩ C)-n(A∩B∩C)}+{n(B ∩ C)-n(A ∩ B ∩ C)}
= n(A ∩ B) +n(B ∩ C ) +n(C ∩ A )- 3n(A ∩ B ∩ C )
= 325+260+235-(3✕125)
= 445
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
SN Dey Class 11 Semester -1 সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
18.একটি দলে কয়েক জন ছাত্র আছে এবং দলের প্রত্যেকে বাংলা,হিন্দি ও ইংরাজি ভাষার মধ্যে কমপক্ষে একটি বলতে পারে । 65 জন বাংলা, 54 জন হিন্দি এবং 37 জন ইংরাজি ভাষায় কথা বলতে পারে; 31 জন বাংলা ও হিন্দি ,17 জন হিন্দি ও ইংরাজি এবং 18 জন বাংলা ও ইংরাজি ভাষায় কথা বলতে পারে । দলের বৃহত্তম ও ক্ষুদ্রতম ছাত্র সংখ্যা নির্ণয় করো ।
সমাধানঃ
বাংলা , হিন্দি ও ইংরাজি তে কথা বলতে পারে এমন ছাত্রের সেট যথাক্রমে A ,B , C
∴ n(A U B U C )= n(A)+n(B)+n(C)-n(A ∩ B)- n(B ∩ C )-n(C∩A )+n(A ∩ B ∩ C)
=65+54+37-31-17-18
=90+ n(A ∩ B ∩C )
এখন, n(A U B U C ) এর মান ক্ষুদ্রতম হবে যদি n(A ∩ B ∩ C ) = 0 হয় ।
∴ n(A U B U C )এর ক্ষুদ্রতম মান = 90+0=90
আবার n(A U B U C ) এর মান বৃহত্তম হবে যদি n(A ∩ B ∩ C ) বৃহত্তম হয় ।
n(A ∩ B ∩ C ) এর বৃহত্তম মান = (A∩B ) , (B∩C ) এবং (C∩A ) এদের ক্ষুদ্রতম মান = 17
∴ n(AUBUC ) এর বৃহত্তম মান = 90+17 = 107
19. সেট প্রক্রিয়া প্রয়োগে প্রমান করো যে , 231 এবং 260 সংখ্যা দুটি পরস্পর মৌলিক ।
সমাধানঃ ধরাযাক, সংখ্যা দুটির গুণনীয়কের সেট যথাক্রমে A ও B ।
A = {1,3,7,11,21,33,77,231}
B = {1,2,4,5,10,13,20,26,52,65,130,260}
এখন A ∩ B = {1}
∴ 231 ও 260 সংখ্যা দুটি পরস্পর মৌলিক ।
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
20. মনে করো A1,A2,A3,…….,A30 এই 30 টি সেটের প্রত্যেকটিতে 5 টি করে এবং B1,B2,B3,…….,Bn এই n সংখ্যক পদের প্রত্যেকটিতে তিনটি করে পদ আছে ।ধরো , A1UA2UA3……..UA30 =B1UB2UB3……..UBn =S , মনে করো S এর প্রত্যেকটি পদ ঠিক দশটি A সেটে এবং নয়টি B সেটে আছে । n এর মান নির্ণয় করো ।
সমাধানঃ S = A1 U A2 U A3 U ………..U A30
প্রতিটি Ai তে 5 টি করে পদ আছে ।
∴ মোট পদসংখ্যা = 30 ✕ 5 =150 টি
কিন্তু S সেটের প্রতিটি পদ 10 টি A সেটের মধ্যে আছে
S সেটের পদসংখ্যা = 150/10 =15
S= B1 U B2 U B3……….U Bn এবং প্রতিটি Bi তে 3 টি করে পদ আছে ।
কিন্তু S সেটের প্রতিটি পদ 9 টি B সেটের মধ্যে আছে
∴S সেটের পদসংখ্যা = 3n/9= n/3
প্রশ্নানুযায়ী,
n/3 = 15
or , n = 45
SN Dey Solution For Class 11 Chapter 1 Set Theory|সৌরেন্দ্রনাথ দে গণিত সমাধান একাদশ শ্রেণি সেট তত্ত্ব
ধন্যবাদ । এই POST টি ভালো লাগলে SHARE করার অনুরোধ রইল । এইরকম আরও সুন্দর সুন্দর POST পেতে ,আমদের FACEBOOK PAGE টি LIKE করুন ।
Parabola solution in S. N. Dey
Wow very help full
I am very happy to use this solution system.
“Sir give me class 11 math solution …
And all subject solution. That is my request”