WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২|গণিত প্রকাশ নবম শ্রেণি সমাধান|গণিত প্রকাশ ক্লাস ৯ কষে দেখি ১২ সমাধান|Gonit prokash Class Nine Koshe Dekhi 12|Gonit Prokash Class IX Koshe Dekhi 12|West Bengal Board Class 9 Math Solution Of Chapter 12.
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২|গণিত প্রকাশ নবম শ্রেণি সমাধান|গণিত প্রকাশ ক্লাস ৯ কষে দেখি ১২ সমাধান|Gonit prokash Class Nine Koshe Dekhi 12|Gonit Prokash Class IX Koshe Dekhi 12|West Bengal Board Class 9 Math Solution Of Chapter 12.
Koshe Dekhi-12|কষে দেখি-১২
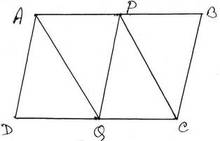
সমাধানঃ ধরি , ABCD সামান্তরিকের AB এবং DC বাহুর মধ্যবিন্দু যথাক্রমে P ও Q । P,C ; A,Q এবং P,Q যুক্ত করা হল ।
প্রমান করতে হবে যে , APCQ চতুর্ভুজাকার ক্ষেত্রের ক্ষেত্রফল = ½ ✕ ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল ।
∴ ∆APQ = ½ সামান্তরিক APQD
আবার , সামান্তরিক BPQC এবং ত্রিভুজ ∆CPQ একই ভূমি QC এবং একই সমান্তরাল যুগল QC ও PB এর মধ্যে অবস্থিত
∴ ∆APQ + ∆CPQ = ½ সামান্তরিক APQD +½ সামান্তরিক BPQC
বা, চতুর্ভুজ APCQ ক্ষেত্রের ক্ষেত্রফল = ½ ✕ সামান্তরিক ABCD [প্রমাণিত ]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
2. ABCD রম্বসের AB ও DC বাহুর মধ্যে দূরত্ব PQ এবং AD ও BC বাহুর মধ্যে দূরত্ব RS ; প্রমাণ করো যে , PQ =RS
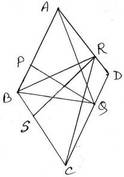
ধরি , ABCD রম্বসের AB ও DC বাহুর মধ্যে দূরত্ব PQ এবং AD ও BC বাহুর মধ্যে দূরত্ব RS , প্রমাণ করতে হবে যে , PQ = RS ।
অঙ্কনঃ A,Q ও B ,Q যুক্ত করা হল । এবং B,R ও C,R যুক্ত করা হল ।
প্রমাণঃ যেহেতু রম্বস একটি সামান্তরিক
∴ সামান্তরিক ABCD এবং ∆ABQ এর একই ভূমি AB এবং একই সমান্তরাল যুগল AB ও CD-এর মধ্যে অবস্থিত
∴ ∆ABQ= ½ সামান্তরিক ABCD
আবার , সামান্তরিক ABCD এবং ∆BCR একই ভূমি BC এবং একই সমান্তরাল যুগল BC ও AD এর মধ্যে অবস্থিত
∴ ∆BCR = ½ সামান্তরিক ABCD
∴ ∆ABQ = ∆BCR
বা, ½ ✕ AB ✕ PQ = ½ ✕ BC ✕ RS [যেহেতু , ত্রিভুজের ক্ষেত্রফল = ½✕ভূমি✕উচ্চতা ]
∴ PQ = RS [যেহেতু , ABCD একটি রম্বস , ∴ AB =BC ] [প্রমাণিত ]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
3. ABCD সামান্তরিকের AB ও DC বাহুর মধ্যবিন্দু যথাক্রমে P এবং Q ; প্রমাণ করতে হবে যে , (i) PBQD একটি সামান্তরিক (ii) ∆PBC = ½ সামান্তরিক PBQD
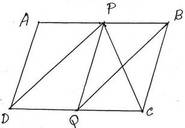
অঙ্কনঃ P ,D ও B ,Q এবং P,C যুক্ত করা হল ।
প্রমাণঃ ABCD একটি সামান্তরিক
∴ AB = DC
∴ PB = DQ [ যেহেতু , P,Q যথাক্রমে AB ও CD এর মধ্যবিন্দু ]
আবার ,যেহেতু ABCD একটি সামান্তরিক
∴ AB || DC
∴ PB || DQ
এখন , চতুর্ভুজ PBQD এর PB || DQ এবং PB =DQ
∴ PBQD একটি সামান্তরিক [ (i) নং প্রমাণিত ]
এখন , ∆PBC ও সামান্তরিক PBCQ একই ভূমি PB ও একই সমান্তরাল যুগল PB ও CD এর মধ্যে অবস্থিত ।
∴ ∆PBC = ½ সামান্তরিক PBQD [(ii) নং প্রমাণিত ]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
4. ABC সমবাহু ত্রিভুজের AB =AC এবং বর্ধিত BC বাহুর উপর P যেকোনো একটি বিন্দু । P বিন্দু থেকে AB এবং AC বাহুর ওপর যথাক্রমে PQ ও PR লম্ব । B বিন্দু থেকে AC বাহুর ওপর লম্ব BS ; প্রমাণ করি যে , PQ –PR =BS
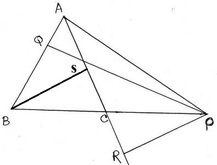
ধরি , ABC সমদ্বিবাহু ত্রিভুজের AB =AC এবং বর্ধিত BC বাহুর উপর P যেকোনো একটি বিন্দু । P থেকে বর্ধিত AB এবং AC বাহুর উপর যথাক্রমে PQ ও PR লম্ব । B বিন্দু থেকে AC বাহুর উপর লম্ব BS
প্রমাণ করতে হবে যে , PQ –PR = BS
অঙ্কনঃ A,P যুক্ত করা হল ।
প্রমাণঃ ABC এর ক্ষেত্রফল = ½ ✕ AC ✕ BS [যেহেতু , ত্রিভুজের ক্ষেত্রফল = ½ ✕ ভূমি ✕ উচ্চতা ]
এবং ACP = ½ ✕ AC ✕ PR [যেহেতু , ত্রিভুজের ক্ষেত্রফল = ½ ✕ ভূমি ✕ উচ্চতা ]
আবার , ∆ABP = ∆ABC + ∆ACP
বা, ½ ✕ AB ✕ PQ = ½ ✕ AC ✕ BS + ½ ✕ AC ✕ PR
বা, ½ ✕ AC ✕ PQ = ½ ✕ AC✕(BS +PR) [যেহেতু , AB =AC ]
বা, PQ = BS+PR
বা, PQ – PR = BS [প্রমাণিত]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
5. ABC সমবাহু ত্রিভুজের বাইরে এবং ABC কৌণিক অঞ্চলের মধ্যে O যেকোনো একটি বিন্দু । O বিন্দু থেকে AB ,BC এবং CA বাহুর উপর লম্ব যথাক্রমে OP , OQ এবং OR; প্রমাণ করি যে , ত্রিভুজটির উচ্চতা = OP +OQ – OR
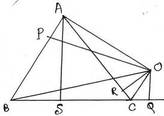
ধরি , ABC সমবাহু ত্রিভুজের বাইরে এবং ABC কৌণিক অঞ্চলের মধ্যে O যেকোনো একটি বিন্দু । O বিন্দু থেকে AB ,BC এবং CAবাহুর উপর লম্ব যথাক্রমে OP ,OQ এবং OR
প্রমাণ করতে হবে যে , ত্রিভুজটির উচ্চতা = OP +OQ – OR
অঙ্কনঃ A বিন্দু থেকে BC –এর ওপর AS লম্ব অঙ্কন করা হল । O,A ;O,B এবং O,C যুক্ত করা হল ।
প্রমাণঃ ∆ABC = ∆AOB +∆BOC-∆AOC
বা, ½ ✕ BC ✕ AS = ½ ✕ AB ✕ OP + ½ ✕ BC ✕ OQ – ½ ✕ AC ✕ OR
বা, BC ✕ AS= BC ✕ OP + BC ✕ OQ – BC ✕ OR [ যেহেতু , AB =AC = BC ]
বা, AS = OP +OQ – OR
∴ ত্রিভুজটির উচ্চতা = OP +OQ –OR [প্রমাণিত ]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
6. ABCD সামান্তরিকের AB বাহুর সমান্তরাল সরলরেখা AD ,AC এবং BC –কে বা তাদের বর্ধিতাংশকে যথাক্রমে E,F ও G বিন্দুতে ছেদ করে । প্রমাণ করি যে , ∆AEG = ∆AFD
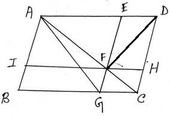
ধরি , ABCD সামান্তরিকের AB বাহুর সমান্তরাল সরলরেখা AD, AC ও BC কে বা তাদের বর্ধিতাংশকে যথাক্রমে E,F ও G বিন্দুতে ছেদ করে ।
প্রমাণ করতে হবে যে , ∆AEG = ∆AFD
অঙ্কনঃ F বিন্দু দিয়ে AD এর সমান্তরাল সরলরেখা AB ও CD কে যথাক্রমে I এবং H বিন্দুতে ছেদ করে ।
প্রমাণঃ AIFE ,BIFG ,CGFH এবং DEFH প্রত্যেকেই সামান্তরিক ।
ABCD সামান্তরিকের কর্ণ AC
∴ ∆ABC = ∆ACD
অনুরূপভাবে , AIF = AEF
এবং FGC = FHC
∴ ∆ABC – ∆AIF – ∆FGC = ∆ACD –∆AEF –∆FHC
∴ সামান্তরিক BIFG = সামান্তরিক DEFH
∴ সামান্তরিক BIFG + সামান্তরিক AIFE = সামান্তরিক AIFE + সামান্তরিক AIFE
∴ সামান্তরিক ABGE = সামান্তরিক AIHD
যেহেতু ∆AFD এবং সামান্তরিক AIHD এর একই ভূমি AD এবং একই সমান্তরাল যুগল AD ও IH এর মধ্যে অবস্থিত ।
∴ ∆AFD = ½ ✕ সামান্তরিক AIHD
আবার সামান্তুরিক ABGE এর মধ্যমা AG
∴ ∆AEG = ½ ✕ সামান্তরিক ABGE
যেহেতু , সামান্তরিক ABGE = সামান্তরিক AIHD
∴ ∆AEG = ∆AFD [প্রমাণিত ]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
7. ABCD সামান্তরিকের DC বাহুর উপর E যেকোনো একটি বিন্দু । বর্ধিত AE , বর্ধিত BC কে F বিন্দুতে ছেদ করে । D ,F যুক্ত করা হল ।প্রমাণ করি যে , (i) ∆ADF = ∆ABE (ii) ∆DEF = ∆BEC
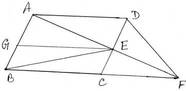
ধরি , ABCD সামান্তরিকের DC বাহুর উপর E যেকোনো বিন্দু । বর্ধিত AE , বর্ধিত BC কে F বিন্দুতে ছেদ করে । D,F যুক্ত করা হল । প্রমান করতে হবে যে , (i) ∆ADF = ∆ABE (ii) ∆DEF = ∆BEC
অঙ্কনঃ E বিন্দু দিয়ে AD এর সমান্তরাল সরলরেখা AB কে G বিন্দুতে ছেদ করে ।
প্রমাণঃ ∆ADF ও সামান্তরিক ABCD এর একই ভূমি AD এবং একই সমান্তরালযুগল AD ও BF এর মধ্যে অবস্থিত ।
∴ ∆ADF = ½ ✕ সামান্তরিক ABCD
আবার , ∆ABE ও সামান্তরিক ABCD এর একই ভূমি AB এবং একই সমান্তরাল যুগল AB ও CD এর মধ্যে অবস্থিত ।
∴ ∆ABE = ½ ✕ সামান্তরিক ABCD
∴ ∆ADF = ∆ABE [(i)নং প্রমাণিত ]
যেহেতু , ∆ADF = ∆ABE\
∴ ∆DEF +∆ADE = ∆AGE +∆BEG
∴ ∆DEF +∆AGE = ∆AGE +∆BEC
[যেহেতু , AGED এর AC কর্ণ এবং BCEG এর BE কর্ণ ]
∴ ∆DEF = ∆BEC [(ii) নং প্রমাণিত ]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
8. সমান ক্ষেত্রফলবিশিষ্ট ABC এবং ABD দুটি ত্রিভুজাকার ক্ষেত্র AB বাহুর বিপরীত দিকে অবস্থিত । প্রমাণ করি যে , AB , CD কে সমদ্বিখন্ডিত করে ।
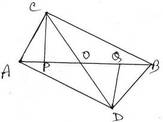
ধরি , সমান ক্ষেত্রফলবিশিষ্ট ABC এবং ABD দুটি ত্রিভুজাকার ক্ষেত্র AB বাহুর বিপরীত দিকে অবস্থিত । প্রমাণ করতে হবে যে , AB , CD –কে সমদ্বিখন্ডিত করে ।
অঙ্কনঃ AB এর উপর C ও D বিন্দু থেকে যথাক্রমে CP এবং DQ লম্ব অঙ্কন করা হল ।
প্রমাণঃ যেহেতু , ABC = ABD
∴ ½ ✕ AB ✕ CP = ½ ✕ AB ✕ DQ
∴ CP =DQ
এখন ∆CPO এবং ∆DQO এর মধ্যে ,
∠CPO = ∠DQO [উভয়ই সমকোণ ]
∠COP = বিপ্রতীপ ∠DOQ
এবং CP = DQ
∴ ∆CPO ≅ ∆DQO
∴ CO = OD
∴ O ,CD এর মধ্যবিন্দু
∴ AB ,CD কে সমদ্বিখন্ডিত করে ।[প্রমাণিত ]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
9. ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D ; CDEF সামান্তরিকটি BC বাহু এবং A বিন্দু দিয়ে BC বাহুর সমান্তরাল সরলরেখার মধ্যে অবস্থিত । প্রমাণ করি যে , ∆ABC = সামান্তরিক CDEF
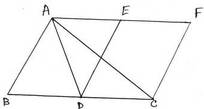
ধরি , ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D ; CDEF সামান্তরিকটি BC বাহু এবং A বিন্দু দিয়ে BC বাহুর সমান্তরাল সরলরেখার মধ্যে অবস্থিত ।
প্রমাণ করতে হবে যে , ∆ABC = সামান্তরিক CDEF
অঙ্কনঃ A ,D যুক্ত করা হল ।
প্রমাণঃ ∆ADC এবং সামান্তরিক CDEF এর একই ভূমি CD এবং একই সমান্তরাল যুগল DC ও EF এর মধ্যে অবস্থিত ।
∴ ∆ADC = ½ সামান্তরিক CDEF
আবার BC বাহুর মধ্যবিন্দু D
∴ AD , ∆ABC এর মধ্যমা
∴ ∆ADC = ½ ∆ABC
∴ ½ ∆ABC = ½ সামান্তরিক CDEF [প্রমাণিত]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
10. ABCD সামান্তরিকের BD কর্ণের উপর P যেকোনো একটি বিন্দু । প্রমাণ করি যে , ∆APD = ∆CPD ।
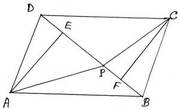
ধরি , ABCD সামান্তরিকের BD কর্ণের উপর P যেকোনো একটি বিন্দু । প্রমাণ করতে হবে যে , ∆APD = ∆CPD
অঙ্কনঃ A ও C বিন্দু দিয়ে BD এর উপর যথাক্রমে AE ও CF লম্ব অঙ্কন করা হল ।
প্রমাণঃ ∆ADE এবং ∆BCF –এর মধ্যে
AD =BC [সামান্তরিকের বিপরীত বাহু ]
∠ADE = একান্তর ∠CBF [ যেহেতু , AD || BC এবং DB ভেদক ]
এবং ∠AED = ∠BFC [উভয়ই সমকোণ ]
∴ ∆ADE ≅ ∆BCF
∴ AE = CF [অনুরূপ বাহু ]
এখন ∆APD ও ∆CPD এর একই ভূমি DP এবং একই উচ্চতা বিশিষ্ট [যেহেতু , AE =CF ]
∴ ∆APD = ∆CPD [প্রমাণিত]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
11. ABC ত্রিভুজের AD এবং BE মধ্যমা । প্রমাণ করি যে , ∆ACD =∆BCE
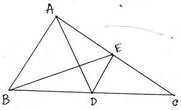
ধরি , ABC ত্রিভুজের AD এবং BE মধ্যমা । প্রমাণ করতে হবে যে , ∆ACD = ∆BCE
অঙ্কনঃ D ,E যুক্ত করা হল ।
প্রমাণঃ AD এবং BE উভয়ই ∆ABC –এর মধ্যমা
∴ D ও E যথাক্রমে BC এবং AC –এর মধ্যবিন্দু
∴ ED || AB
এখন ∆ADE এবং ∆BDE ত্রিভুজদ্বয় একই ভূমি DE এবং একই সমান্তরাল যুগল ED ও AB এর মধ্যে অবস্থিত
∴ ∆ADE = ∆BDE
উভয়পক্ষে ∆DEC যোগ করে পাই ,
∆ADE + ∆DEC = ∆BDE + ∆DEC
সুতরাং , ∆ACD =∆BCE [প্রমাণিত ]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
12. ABC ত্রিভুজের BC বাহুর সমান্তরাল সরলরেখা AB এবং AC বাহুকে যথাক্রমে P এবং Q বিন্দুতে ছেদ করে । CP এবং BQ পরস্পরকে X বিন্দুতে ছেদ করে । প্রমাণ করি যে , (i) ∆BPQ =∆CPQ (ii) ∆BCP = ∆BCQ (iii) ∆ACP = ∆ABQ (iv) ∆BXP = ∆CXQ
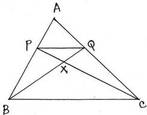
ধরি ,ABC ত্রিভুজের BC বাহুর সমান্তরাল সরলরেখা AB ও AC বাহকে যথাক্রমে P এবং Q বিন্দুতে ছেদ করে । CP এবং BQ পরস্পরকে X বিন্দুতে ছেদ করে ।
প্রমাণ করতে হবে যে , (i) ∆BPQ =∆CPQ (ii) ∆BCP =∆BCQ (iii) ∆ACP =∆ABQ (iv) ∆BXP = ∆CXQ
প্রমাণঃ ∆BPQ ও ∆CPQ এর একই ভূমি PQ এবং একই সমান্তরাল যুগল PQ ও BC –এর মধ্যে অবস্থিত
∴ ∆BPQ =∆CPQ [(i)নং প্রমাণিত ]
∆BCP ও ∆BCQ এর একই ভূমি BC এবং একই সমান্তরাল যুগল PQ ও BC এর মধ্যে অবস্থিত
∴ ∆BCP = ∆BCQ [(ii) নং প্রমাণিত ]
যেহেতু , ∆CPQ = ∆BPQ
∴ ∆CPQ +∆APQ = ∆BPQ +∆APQ
∴ ∆ACP = ∆ABQ [(iii) নং প্রমাণিত ]
যেহেতু , ∆BPQ = ∆CPQ
∴ ∆BPQ – ∆PQX = ∆CPQ – ∆PQX
∴ ∆BXP = ∆CXQ [(iv)নং প্রমাণিত ]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
13. ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D এবং BC বাহুর উপর P যেকোনো একটি বিন্দু । P ,A যুক্ত করি । D বিন্দু দিয়ে PA সরলরেখাংশের সমান্তরাল সরলরেখা AB বাহুকে Q বিন্দুতে ছেদ করে । প্রমাণ করি যে ,(i) ∆ADQ = ∆PDQ (ii) ∆BPQ = ½ ∆ABC
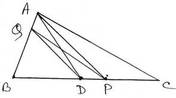
ধরি , ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D এবং BC বাহুর উপর P যেকোনো একটি বিন্দু । P ,A যুক্ত করা হল ।D বিন্দু দিয়ে PA সরলরেখাংশের সমান্তরাল সরলরেখা AB বাহুকে Q বিন্দুতে ছেদ করে । প্রমান করতে হবে যে ,(i) ∆ADQ = ∆PDQ (ii) ∆BPQ = ½ ∆ABC
প্রমাণঃ ∆ADQ এবং ∆PDQ ত্রিভুজদ্বয় একই ভূমি QD এবং একই সমান্তরাল যুগল QD ও AP এর মধ্যে অবস্থিত
∴ ∆ADQ = ∆PDQ [(i) নং প্রমাণিত ]
∆BPQ = ∆BDQ +∆PDQ
বা, ∆BPQ = ∆BDQ +∆ADQ [ যেহেতু , ADQ = PDQ ]
বা, ∆BPQ = ∆ABD
বা, ∆BPQ = ½ ∆ABC [যেহেতু , AD মধ্যমা ]
∴ ∆BPQ = ½ ∆ABC [(ii)নং প্রমাণিত]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
14.ABC ত্রিভুজে AB =AC ;B ও C বিন্দু থেকে AB ও AC বাহুর উপর লম্ব যথাক্রমে AC ও AB বাহুকে E ও F বিন্দুতে ছেদ করেছে । প্রমাণ করি যে , FE || BC
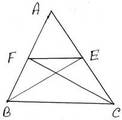
ধরি , ABC ত্রিভুজে AB =AC ;B বিন্দু থেকে AC ও AB বাহুর উপর লম্ব যথাক্রমে AC ও AB বাহুকে E ও F বিন্দুতে ছেদ করে । প্রমাণ করতে হবে যে , FE || BC
প্রমাণঃ ∆ABC = ½ ✕ AB ✕ CF
আবার, ∆ABC = ½ ✕ AC ✕ BE
∴ ½ ✕ AB ✕ CF = ½ ✕ AC ✕ BE
বা, CF =BE [যেহেতু , AB =AC ]
এখন ∆BCE এবং ∆BFC এর মধ্যে
∠BEC = ∠BFC [উভয়ই সমকোণ ]
CF = BE
এবং BC সাধারণ বাহু
∴ ∆BEC ≅ ∆BFC
এখন BEC এবং BFC এর একই ভূমি BC এবং তাদের ক্ষেত্রফল সমান সুতরাং তারা BC ভূমির একই পার্স্বে এবং একই সমান্তরালযুগলের মধ্যে অবস্থিত ।
∴ FE || BC [প্রমাণিত]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
15. ABC ত্রিভুজে ∠ABC = ∠ACB ,∠ABC ও ∠ACB কোণের সমদ্বিখণ্ডকদ্বয় AC এবং AB বাহুকে যথাক্রমে E ও F বিন্দুতে ছেদ করে । প্রমাণ করি যে , FE || BC
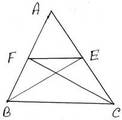
ধরি , ABC ত্রিভুজে ∠ABC = ∠ACB ; ∠ABC ও ∠ACB কোণের সমদ্বিখন্দকদ্বয় AC এবং AB বাহুকে যথাক্রমে E ও F বিন্দুতে ছেদ করেছে । প্রমাণ করতে হবে যে , FE || BC
অঙ্কনঃ E ,F যুক্ত করা হল
প্রমাণঃ যেহেতু, BE ও CF যথাক্রমে ∠ABC ও ∠ACB কোণের সমদ্বিখণ্ডক এবং ∠ABC = ∠ACB
∴ ∠EBC = ∠FCB
এখন ∆BEC এবং ∆BFC এর মধ্যে
∠EBC = ∠FCB
∠ECB = ∠BFC [যেহেতু,∠ABC = ∠ACB ]
এবং BC সাধারণ বাহু
∴ ∆BEC ≅ ∆BFC
এখন ∆BEC এবং ∆BFC ত্রিভুজদ্বয়ের একই ভূমি BC এবং এদের ক্ষেত্রফল সমান এবং তারা BC ভূমির একই পার্শ্বে অবস্থিত ।
∴ FE || BC [প্রমাণিত]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
16. সমান ক্ষেত্রফল বিশিষ্ট ABCD ও AEFG সামান্তরিক আকারের ক্ষেত্র দুটির ∠A সাধারণ এবং E ,AB বাহুর উপর অবস্থিত । প্রমাণ করি যে , DE || FC
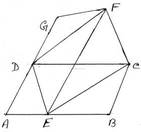
ধরি , সমান ক্ষেত্রফলবিশিষ্ট ABCD ও AEFG সামান্তরিক আকারের ক্ষেত্রদুটির ∠A সাধারণ এবং E , AB বাহুর উপর অবস্থিত ।
প্রমাণ করতে হবে যে , DE || FC
অঙ্কনঃ D,E এবং C,E যুক্ত করা হল ।
প্রমাণঃ DEC এবং সামান্তরিক ABCD এর একই ভূমি DC এবং একই সমান্তরাল যুগল DC ও AB এর মধ্যে অবস্থিত ।
∴ ∆DEC = ½ সামান্তরিক ABCD
আবার , ∆DEF এবং সামান্তরিক AEFG এর একই ভূমি EF এবং একই সমান্তরাল যুগল EF ও AG এর মধ্যে অবস্থিত ।
∴ ∆DEF = ½ সামান্তরিক AEFG
আবার যেহেতু ABCD ও AEFG সামান্তরিক আকারের ক্ষেত্র দুটির ক্ষেত্রফল সমান ।
∴ ∆DEC = ∆DEF
এখন , ∆DEC ও ∆DEF এর একই ভূমি DE এবং ক্ষেত্রফল সমান এবং তারা DE এর একি পার্স্বে অবস্থিত ।
∴ DE || FC [প্রমাণিত]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
17. ABCD একটি সামান্তরিক এবং ABCE একটি চতুর্ভুজ । AC কর্ণ ABCE চতুর্ভুজ আকারের ক্ষেত্রটিকে দুটি সমান অংশে বিভক্ত করে । প্রমাণ করি , AC || DE
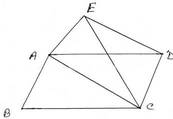
ধরি , ABCD একটি সামান্তরিক এবং ABCE একটি চতুর্ভুজ । AC কর্ণ ABCE চতুর্ভুজ আকারের ক্ষেত্রটিকে দুটি সমান অংশে বিভক্ত করে । প্রমাণ করতে হবে যে , AC || DE
প্রমাণঃ সামান্তরিক ABCD এর কর্ণ AC
∴ ∆ABC = ∆ADC
আবার যেহেতু AC কর্ণ ABCE চতুর্ভুজ আকারের ক্ষেত্রটিকে দুটি সমান অংশে বিভক্ত করে ।
∴ ∆ABC = ∆ACE
∴ ∆ADC = ∆ACE
এখন ∆ADC ও ∆ACE এর একই ভূমি AC এবং তাদের ক্ষেত্রফল সমান এবং তারা AC এর একই পার্শ্বে অবস্থিত ।
∴ AC || DE [প্রমাণিত]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
18. ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D ; P এবং Q যথাক্রমে BC ও BA বাহুর উপর এমনভাবে অবস্থিত যে , ∆BPQ = ½ ∆ABC ;প্রমাণ করি যে , DQ || PA
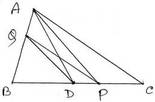
ধরি , ∆ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D ; P এবং Q জথাক্রমে BC ও BA বাহুর উপর এমন ভাবে অবস্থিত যে , ∆BPQ = ½ ∆ABC , প্রমাণ করতে হবে যে , DQ || PA
অঙ্কনঃ A,D যুক্ত করা হল ।
প্রমাণঃ ∆BPQ = ½ ∆ABC =∆ABD [যেহেতু ,AD মধ্যমা ]
∴ ∆BDQ +∆DPQ = ∆BDQ +∆ADQ
অর্থাৎ , ∆DPQ = ∆ADQ
এখন ,∆DPQ ও ∆ADQ –এর একই ভূমি DQ এবং তাদের ক্ষেত্রফল সমান এবং তারা DQ –এর একই পার্স্বে অবস্থিত ।
∴ DQ || PA [প্রমাণিত ]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
19. ABCD সামান্তরিকের AB , BC, CD এবং DA বাহুর মধ্যবিন্দু যথাক্রমে E,F ,G ও H প্রমাণ করি যে , (i) EFGH একটি সামান্তরিক (ii) EFGH একটি সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল ABCD সামান্তরিক আকারের ক্ষেত্রের ক্ষেত্রফলের অর্ধেক ।
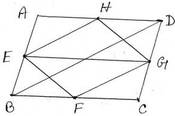
ধরি ,ABCD সামান্তরিকের AB ,BC,CD এবং DA বাহুর মধ্যবিন্দু যথাক্রমে E,F,G ও H
প্রমাণ করতে হবে যে , (i) EFGH একটি সামান্তরিক (ii) EFGH সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফলের অর্ধেক ।
অঙ্কনঃ D,Bও E,G যুক্ত করা হল ।
প্রমাণঃ ∆ABD এর AB এবং AD বাহুর মধ্যবিন্দু যথাক্রমে E এবং H
∴ EH = ½ DB এবং EH || BD
অনুরূপভাবে ,∆BDC এর BC এবং CD বাহুর মধ্যবিন্দু যথাক্রমে F ও G
∴ FG = ½ BD এবং FG || BD
∴ EF = FG এবং EH || FG
∴ EFGH একটি সামান্তরিক [(i) নং প্রমাণিত ]
আবার ,ABCD সামান্তরিকের AB ও DC বাহুর মধ্যবিন্দু যথাক্রমে E ও G
∴ EG || BC || AD
এখন , ∆EHG ও সামান্তরিক BCGE এর একই ভূমি EG এবং তারা একই সমান্তরাল যুগল EG ও BC এর মধ্যে অবস্থিত ।
∴ ∆EFG = ½ সামান্তরিক BCGE
একিভাবে , ∆EHG ও সামান্তরিক AEGD এর একই ভূমি EG এবং তারা একই সমান্তরালযুগল EG ও AD এর মধ্যে অবস্থিত ।
∴ ∆EHG = ½ সামান্তরিক AEGD
∴ ∆EFG + ∆EHG = ½ সামান্তরিক BCGE + ½ সামান্তরিক AEGD
∴ সামান্তরিক EFGH = ½ (সামান্তরিক BCGE + সামান্তরিক AEGD )
অর্থাৎ , সামান্তরিক EFGH = ½ সামান্তরিক ABCD [(ii) নং প্রমাণিত]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
20. ABCD ট্রাপিজিয়ামের AB || DC এবং BC বাহুর মধ্যবিন্দু E ; প্রমাণ করি যে , AED ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল = ½✕ ABCD ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল ।
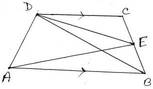
ধরি , ABCD ট্রাপিজিয়ামের AB || DC এবং BC বাহুর মধ্যবিন্দু E
প্রমাণ করতে হবে যে , AED ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল = ½ ✕ ABCD ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল ।
অঙ্কনঃ A,C এবং B,D যুক্ত করা হল ।
প্রমাণঃ ∆ABC এর AE মধ্যমা
∴ ∆ABE = ∆AEC = ½ ∆ABC
আবার, ∆BDC এর DE মধ্যমা
∴ ∆CDE = ∆BDE = ½ ∆BDC
এখন , ∆BDC এবং ∆ADC এর একই ভূমি DC এবং একই সমান্তরালযুগল DC ও AB এর মধ্যে অবস্থিত ।
∴ ∆BDC = ∆ADC
∴ ∆CDE = ½ ∆BDC = ½ ∆ADC
এখন , ∆AED = ট্রাপিজিয়াম ABCD – (∆ABE +∆CDE )
বা, ∆AED = ট্রাপিজিয়াম ABCD – ( ½ ∆ABC + ½ ∆ADC)
বা, ∆AED = ট্রাপিজিয়াম ABCD – ½ (∆ABC + ∆ADC)
বা, ∆AED = ট্রাপিজিয়াম ABCD – ½ ট্রাপিজিয়াম ABCD
বা, ∆AED = ½ ট্রাপিজিয়াম ABCD [প্রমাণিত ]
WBBSE Class 9 Math Koshe Dekhi 12|ক্ষেত্রফল সংক্রান্ত উপপাদ্য কষে দেখি ১২
21. বহু বিকল্পীয় প্রশ্ন(M.C.Q):
(i) ∆ABC এর BC ,CA এবং AB বাহুর মধ্যবিন্দু যথাক্রমে D,E এবং F ; যদি ABC = 16 বর্গ সেমি. হয় তাহলে FBCE ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল
(a) 40 বর্গ সেমি.
(b) 8 বর্গ সেমি.
(c ) 12 বর্গ সেমি.
(d) 100 বর্গ সেমি.
Ans: (c ) 12 বর্গ সেমি.
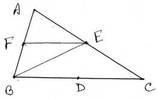
সমাধানঃ B,E যোগ করা হল ।
∆ABC এর BC মধ্যমা ।
∴ ∆ABE = ½ ∆ABC = 16/2 বর্গসেমি. = 8 বর্গসেমি.
আবার , ∆ABE এর EF মধ্যমা ।
∴ ∆AEF = ½ ∆ABE = 8/2 বর্গসেমি. = 4 বর্গসেমি.
∴ ট্রাপিজিয়াম FBCE = ∆ABC – ∆AFE = (16 -4) বর্গসেমি. = 12 বর্গসেমি.
(ii) A ,B,C ও D যথাক্রমে PQRS সামান্তরিকের PQ , QR , RS ,SP বাহুর মধ্যবিন্দু । PQRS সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল = 36 বর্গসেমি. হলে ,ABCD ক্ষেত্রের ক্ষেত্রফল
(a) 24 বর্গসেমি.
(b)18 বর্গসেমি.
(c ) 30 বর্গসেমি.
(d) 36 বর্গসেমি.
Ans: (b)18 বর্গসেমি.
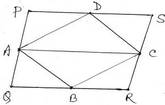
∴ PS || AC || QR
∴ PACS এবং AQRC প্রত্যেকেই সামান্তরিক ।
∴ ∆ABC = ½ সামান্তরিক AQRC এবং ∆ADC = ½ সামান্তরিক APSC [যেহেতু ,একই ভূমি ও একই সমান্তরালযুগলের মধ্যে অবস্থিত ত্রিভুজের ক্ষেত্রফল সামান্তরিকের ক্ষেত্রফলের অর্ধেক ]
∴ ∆ABC + ∆ADC = ½ সামান্তরিক AQRC + ½ সামান্তরিক APSC
বা, সামান্তরিক ABCD = ½ (সামান্তরিক AQRC + সামান্তরিক APSC )
বা, সামান্তরিক ABCD = ½ ✕ সামান্তরিক PQRS
বা, সামান্তরিক ABCD = (½ ✕ 36) বর্গসেমি. = 18 বর্গসেমি.
(iii) ABCD সামান্তরিকের ভিতর O যেকোনো একটি বিন্দু ।∆AOB + ∆COD = 16 বর্গসেমি. হলে , ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল
(a) 8 বর্গসেমি.
(b) 4 বর্গসেমি.
(c ) 32 বর্গসেমি.
(d) 64 বর্গসেমি.
Ans: (c ) 32 বর্গসেমি.
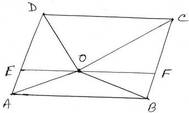
সমাধান: O বিন্দু দিয়ে AB ও CD বাহুর সমান্তরাল সরলরেখা টানা হল যা AD ও BC বাহুকে যথাক্রমে E ও F বিন্দুতে ছেদ করেছে ।
∴ AB || EF || DC
∴ CDEF এবং EABF প্রত্যেকেই সামান্তরিক
∴ ∆AOB = ½সামান্তরিক EABF এবং ∆COD = ½ সামান্তরিক CDEF
∴ AOB +COD = ½সামান্তরিক EABF + ½ সামান্তরিক CDEF
বা, 16 = ½ (সামান্তরিক EABF + সামান্তরিক CDEF )
বা, (সামান্তরিক EABF + সামান্তরিক CDEF ) = 32
বা, সামান্তরিক ABCD এর ক্ষেত্রফল = 32বর্গসেমি.
(iv) ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D , BD বাহুর মধ্যবিন্দু E এবং AE –এর মধ্যবিন্দু O ; BOE ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(a) 1/3 ✕ ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(b) ¼ ✕ ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(c ) 1/6 ✕ ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(d) 1/8 ✕ ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
Ans: (d) 1/8 ✕ ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
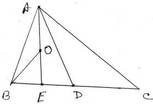
সমাধানঃ ∆BOE = ½ ∆ABE [যেহেতু , ABE ত্রিভুজের OB মধ্যমা ]
বা, ∆BOE = ½ ( ½ ∆ABD ) [ যেহেতু , ABD ত্রিভুজের AE মধ্যমা ]
বা, ∆BOE = ¼ ∆ABD
বা, ∆BOE = ¼ ( ½ ∆ABC) [যেহেতু , ABC ত্রিভুজের মধ্যমা AD]
বা, ∆BOE = 1/8 ∆ABC
(v) একটি সামান্তরিক আকারের ক্ষেত্র , একটি আয়তক্ষেত্র এবং একটি ত্রিভুজাকার ক্ষেত্র একই ভূমি ও একই সমান্তরালযুগলের মধ্যে অবস্থিত এবং তাদের ক্ষেত্রফল যথাক্রমে P ,Q ও T হলে
(a) P = R =2T
(b) P =R = T/2
(c ) 2P = 2R = T
(d) P =R =T
Ans: (a) P = R =2T
সমাধানঃ একই ভূমি এবং একই সমান্তরালযুগলের মধ্যে অবস্থিত, একটি সামান্তরিক আকারের ক্ষেত্রফল = একটি আয়তক্ষেত্রের ক্ষেত্রফল = 2 ✕ একটি ত্রিভুজের ক্ষেত্রফল
বা, P =R = 2T
22. সংক্ষিপ্ত উত্তরধর্মী প্রশ্নঃ
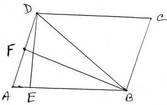
সমাধানঃ B,D যুক্ত করা হল ।
AD কে ভূমি ধরে ,ADB এর ক্ষেত্রফল = ½ ✕ AD ✕ BF
আবার, AB কে ভূমি ধরে , ADB এর ক্ষেত্রফল = ½ ✕ AB ✕ DE
∴ ½ ✕ AD ✕ BF = ½ ✕ AB ✕ DE
বা, ½ ✕ 8 ✕ BF = ½ ✕ 10 ✕ 6
বা, 4 ✕ BF = 30
বা, BF = 30/4
বা, BF = 7.5
∴ BF বাহুর দৈর্ঘ্য 7.5 সেমি. । [উত্তর]
(ii) ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল 100 বর্গএকক ; BC বাহুর মধ্যবিন্দু P ; ABP ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল কত তা লিখি ।
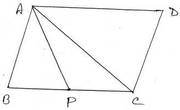
সমাধানঃ AC কর্ণ টানা হল ।
∴ ∆ABC = ½ সামান্তরিক ABCD –এর ক্ষেত্রফল
আবার , ∆ABP = ½ ∆ABC [যেহেতু ,AP ,∆ABC এর মধ্যমা ]
∴ ∆ABP = ½ ∆ABC = ½ ( ½ ABCD ) = ¼ ABCD
∴ ABP ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল ABCD সামান্তরিকের ক্ষেত্রফলের ¼ অংশ ।
∴ ABP ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল = (1/4 ✕ 100) বর্গসেমি. = 25 বর্গসেমি. [উত্তর]
(iii) ABC ত্রিভুজের AD মধ্যমা এবং AC বাহুর উপর P এমন একটি বিন্দু যাতে ADP –এর ক্ষেত্রফল : ABD এর ক্ষেত্রফল = 2:3 হয় । PDC এর ক্ষেত্রফল : ABC এর ক্ষেত্রফল কত তা লিখি ।
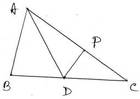
সমাধানঃ যেহেতু , ABC ত্রিভুজের AD মধ্যমা ।
∴ ∆ABD = ∆ADC
এবং ∆ABC = 2∆ADC
∆ADP এর ক্ষেত্রফল : ∆ABD –এর ক্ষেত্রফল = 2:3
∴ ∆ADP –এর ক্ষেত্রফল = 2/3 ✕ ∆ABD এর ক্ষেত্রফল = 2/3 ✕ ∆ADC এর ক্ষেত্রফল
∴ ∆PDC –এর ক্ষেত্রফল = ∆ADC এর ক্ষেত্রফল – ∆ADP এর ক্ষেত্রফল = ∆ADC এর ক্ষেত্রফল – 2/3 ✕ ∆ADC এর ক্ষেত্রফল = 1/3 ∆ADC –এর ক্ষেত্রফল
∴ ∆PDC এর ক্ষেত্রফল :∆ABC এর ক্ষেত্রফল
= 1/3∆ADC : 2∆ADC
= 1/3 : 2
= 1:6 [উত্তর]
(iv) ABDE একটি সামান্তরিক । F , AD বাহুর মধ্যবিন্দু । ABD ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল 20 বর্গসেমি. হলে AEF ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল কত তা লিখি ।
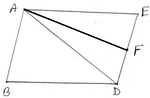
সমাধানঃ ABDE সামান্তরিকের AD মধ্যমা ।
∴ ∆ADE = ∆ABD = 20 বর্গসেমি.
আবার , ∆ADE এর AF মধ্যমা ।
∴ ∆AEF = ½ ∆ADE = 10 বর্গসেমি. [উত্তর]
(V) PQRS একটি সামান্তরিক ।X ও Y যথাক্রমে PQ ও SR বাহুর মধ্যবিন্দু । কর্ণ SQ যুক্ত করা হল । সামান্তরিক XQRY আকার ক্ষেত্রের ক্ষেত্রফল : QSR ত্রিভুজকার ক্ষেত্রের ক্ষেত্রফল কত তা লিখি ।
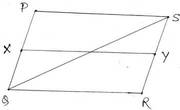
সমাধানঃ যেহেতু ,X এবং Y যথাক্রমে PQ এবং RS বাহুর মধ্যবিন্দু
∴ XQRY আকার ক্ষেত্রের ক্ষেত্রফল = ½ PQRS সামান্তরিকের ক্ষেত্রফল
আবার , PQRS সামান্তরিকের কর্ণ SQ
∴ QSR ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল = ½ PQRS সামান্তরিকের ক্ষেত্রফল
∴ XQRY আকার ক্ষেত্রের ক্ষেত্রফল = QSR ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
∴ XQRY আকার ক্ষেত্রের ক্ষেত্রফল : QSR ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল = 1:1 [উত্তর ]
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
ধন্যবাদ । এই POST টি ভালো লাগলে SHARE করার অনুরোধ রইল । এইরকম আরও সুন্দর সুন্দর POST পেতে , আমাদের FACEBOOK PAGE টি LIKE করুন ।