WBBSE Class 9 Math Koshe Dekhi 17|সমবিন্দু সংক্রান্ত উপপাদ্য কষে দেখি ১৭|Ganit Prakash Class 9 Solution Of Chapter 17|Ganit Prakash Class Nine Solution Koshe Dekhi 17|West Bengal Board Class Nine Math Book Solution| গণিত প্রকাশ নবম শ্রেণি কষে দেখি ১৭ সমাধান |গণিত প্রকাশ ক্লাস ৯ কষে দেখি ১৭ সমবিন্দু সংক্রান্ত উপপাদ্য সমাধান
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
WBBSE Class 9 Math Koshe Dekhi 17|সমবিন্দু সংক্রান্ত উপপাদ্য কষে দেখি ১৭|Ganit Prakash Class 9 Solution Of Chapter 17|Ganit Prakash Class Nine Solution Koshe Dekhi 17|West Bengal Board Class Nine Math Book Solution| গণিত প্রকাশ নবম শ্রেণি কষে দেখি ১৭ সমাধান |গণিত প্রকাশ ক্লাস ৯ কষে দেখি ১৭ সমবিন্দু সংক্রান্ত উপপাদ্য সমাধান
Koshe Dekhi- 17|কষে দেখি -১৭
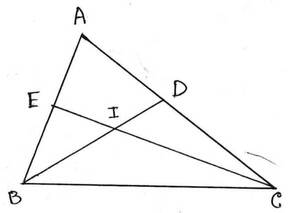
1. ABC ত্রিভুজে B ও C এর অন্তসমদ্বিখন্ডক I বিন্দুতে ছেদ করেছে ।প্রমাণ করি যে , ∠BIC = 90º + ∠BAC/2

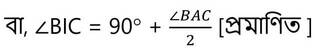
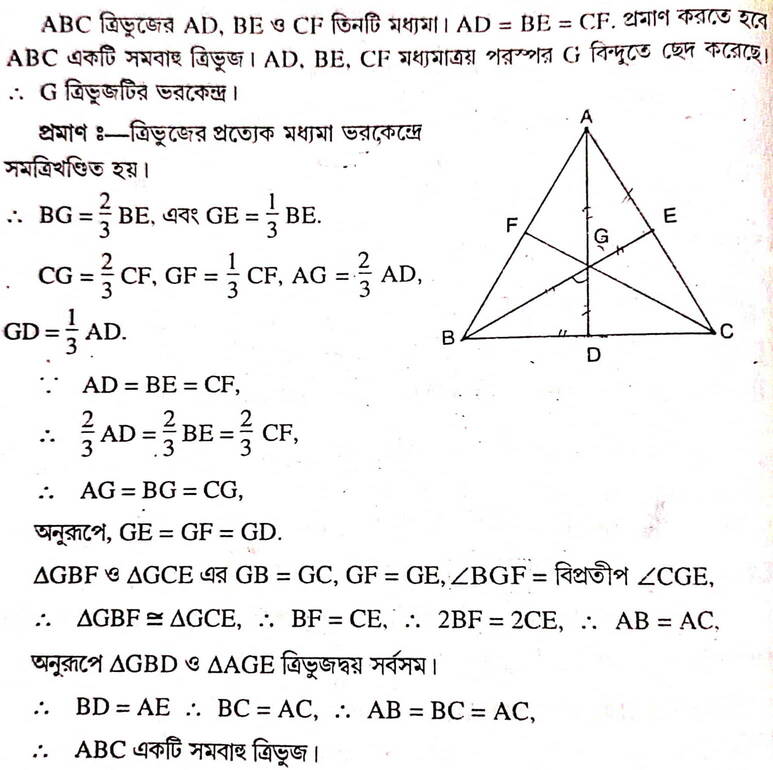
2. একটি ত্রিভুজের তিনটি মধ্যমার দৈর্ঘ্য সমান হলে প্রমাণ করি যে , ত্রিভুজটি সমবাহু ।
| WBBSE Class 9 Math Koshe Dekhi 17|সমবিন্দু সংক্রান্ত উপপাদ্য কষে দেখি ১৭|Ganit Prakash Class 9 Solution Of Chapter 17|Ganit Prakash Class Nine Solution Koshe Dekhi 17|West Bengal Board Class Nine Math Book Solution| গণিত প্রকাশ নবম শ্রেণি কষে দেখি ১৭ সমাধান |গণিত প্রকাশ ক্লাস ৯ কষে দেখি ১৭ সমবিন্দু সংক্রান্ত উপপাদ্য সমাধান |
3. প্রমাণ করি সমবাহু ত্রিভুজের পরিকেন্দ্র , অন্তকেন্দ্র ,ভরকেন্দ্র ও লম্ববিন্দু সমপাতিত হয় ।

ধরি , সমবাহু ত্রিভুজ ABC-এর মধ্যমাত্রয় AD ,BE এবং CF পরস্পরকে G বিন্দুতে ছেদ করেছে ।
প্রমাণ করতে হবে যে , সমবাহু ত্রিভুজটির পরিকেন্দ্র ,অন্তকেন্দ্র ,ভরকেন্দ্র ও লম্ববিন্দু সমপাতিত হয়েছে ।
প্রমাণঃ ∆ABC –এর মধ্যমা ত্রয় AD ,BE এবং CF পরস্পরকে G বিন্দুতে ছেদ করেছে ।
∴ ∆ABC -এর ভরকেন্দ্র G
আবার আমরা জানি সমবাহু ত্রিভুজের উচ্চতাই হল মধ্যমা ।
∴ ∆ABC এর লম্ববিন্দু G
আমরা জানি , সমবাহু ত্রিভুজের অন্তঃবৃত্তের ব্যাসার্ধ তার উচ্চতার দৈর্ঘ্যের এক-তৃতীয়াংশ ।
∴ GD = GE = GF = অন্তঃবৃত্তের ব্যাসার্ধ
∴ অন্তঃবৃত্তের কেন্দ্র হল G
আমরা জানি ,সমবাহু ত্রিভুজের পরিবৃত্তের ব্যাসার্ধ তার উচ্চতার দুই – তৃতীয়াংশ ।
∴ AG = BG =CG =পরিবৃত্তের ব্যাসার্ধ
∴ পরিবৃত্তের কেন্দ্রটি হল G
∴ সমবাহু ত্রিভুজের পরিকেন্দ্র , অন্তঃকেন্দ্র , ভরকেন্দ্র ও লম্ববিন্দু সমপাতিত হয় । [প্রমাণিত ]
4. ABC ত্রিভুজের AD ,BE এবং CF মধ্যমা । প্রমাণ করি যে , ABC ও DEF ত্রিভুজের ভরকেন্দ্র একই বিন্দু ।
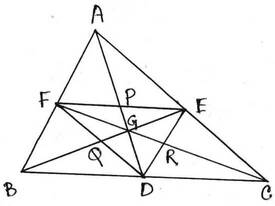
ধরি , ABC এর AD,BE এবং CF মধ্যমা ত্রয় পরস্পরকে G বিন্দুতে ছেদ করেছে । প্রমাণ করতে হবে যে , ABC ও DEF ত্রিভুজের ভরকেন্দ্র একই বিন্দু । অর্থাৎ , ∆DEF এর ভরকেন্দ্র G প্রমাণ করলেই হবে , ∆ABC এবং ∆DEF এর ভরকেন্দ্র একই বিন্দু ।
প্রমাণঃ ∆ABC –এর AB এবং AC বাহুর মধ্যবিন্দু যথাক্রমে F এবং E
∴ FE || BC এবং EF = ½ BC
আবার D ,BC এর মধ্যবিন্দু
∴ EF =BD
এখন BDEF চতুর্ভুজের , FE || BD [∵ FE ||BC] এবং FE =BD
∴ BDEF একটি সামান্তরিক ।
অনুরূপ ভাবে প্রমাণ করা যায় যে , DCEF এবং AFDE উভয়ই সামান্তরিক ।
আমরা জানি সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে ।
∴ BDEF সামান্তরিক থেকে পাই ,
FQ = QD , ∴ Q ,FD এর মধ্যবিন্দু ।
DCEF সামান্তরিক থেকে পাই ,
DR =RE , ∴ R ,DE এর মধ্যবিন্দু ।
এবং AFDE সামান্তরিক থেকে পাই ,
FP = PE, ∴ P ,FE এর মধ্যবিন্দু ।
∴ ∆DEF –এর মধ্যমা তিনটি হল DP ,EQ এবং FR ,যারা পরস্পরকে G বিন্দুতে ছেদ করেছে ।
∴ ∆DEF –এর ভরকেন্দ্র G ।
∴ ABC ও DEF ত্রিভুজের ভরকেন্দ্র একই বিন্দু । [প্রমাণিত ]
5. প্রমাণ করি যে একটি ত্রিভুজের দুটি মধ্যমার দৈর্ঘ্যের সমষ্টি তৃতীয় মধ্যমার দৈর্ঘ্য অপেক্ষা বৃহত্তর।

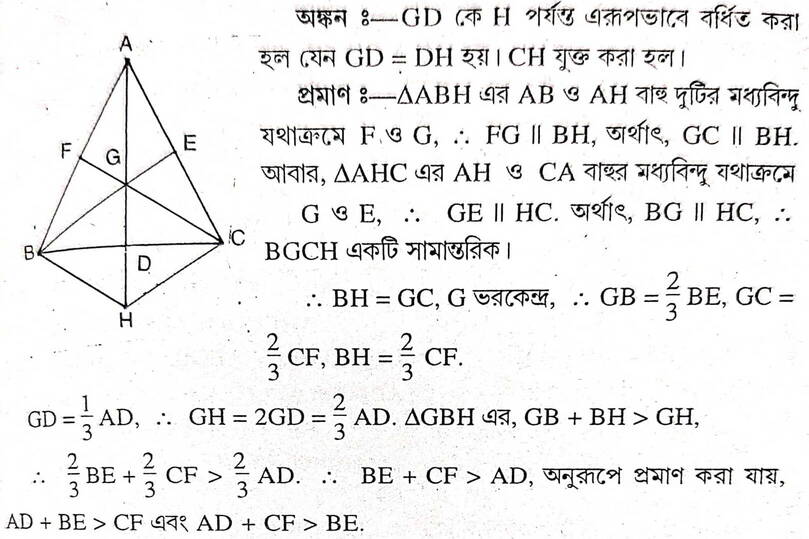
6. ABC ত্রিভুজের AD ,BE ও CF মধ্যমা । প্রমাণ করি যে ,
(i) 4(AD +BE+CF) > 3(AB+BC +CA)
(ii) 3(AB+BC+ CA) > 2(AD+BE +CF)
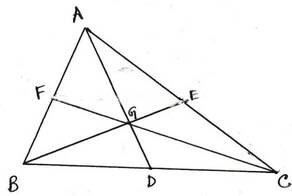
ধরি , ABC এর AD ,BE এবং CF মধ্যমাত্রয় পরস্পরকে G বিন্দুতে ছেদ করেছে । প্রমাণ করতে হবে যে , (i) 4(AD+BE+CF) > 3(AB+BC+CA)
(ii) 3(AB+BC+CA) > 2(AD+BE+CF)
প্রমাণঃ যেহেতু ত্রিভুজের ভরকেন্দ্র মধ্যমাকে 2:1 অনুপাতে বিভক্ত করে
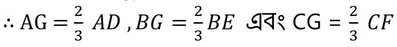
এখন BGC থেকে পাই ,
BG+GC > BC
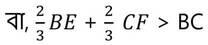
বা, 2BE +2CF > 3BC —(i)
অনুরূপভাবে AGC থেকে পাই ,
2AD+2CF > 3AC —–(ii)
এবং AGB থেকে পাই ,
2AD +2BE > 3AB —–(iii)
(i) ,(ii) ও (iii) নং সমীকরণ যোগ করে পাই ,
2BE+2CF+2AD + 2CF + 2AD+ 2BE > 3BC+3AC+3AB
বা 4 (AD+BE+CF) > 3(AB+BC+CA) [(i) নং প্রমাণিত ]
∆ACD থেকে পাই ,
AC +CD > AD
বা, AC + ½ BC > AD — (iv) [∵ D,BC এর মধ্যবিন্দু ]
একই ভাবে ∆ABE থেকে পাই , AB + ½ AC > BE —(v)
এবং ∆BFC থেকে পাই , BC + ½ AB >CF —(vi)
(iv) ,(v) এবং (vi) নং সমীকরণ যোগ করে পাই ,
AC+ ½ BC +AB+ ½ AC + BC + ½ AB > AD+BE +CF
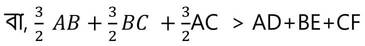
বা, 3(AB+BC+AC) > 2(AD+BE+CF) [(ii) নং প্রমাণিত ]
7. ABC এর AD ,BE এবং CF মধ্যমা তিনটি G বিন্দুতে পরস্পকে ছেদ করেছে। ∆ABC –এর ক্ষেত্রফল 36 বর্গসেমি. হলে (i) ∆AGB –এর ক্ষেত্রফল (ii) ∆CGE –এর ক্ষেত্রফল (iii) চতুর্ভুজ BDGF এর ক্ষেত্রফল নির্ণয় করো।



8. ABC ত্রিভুজের AD ,BE ও CF মধ্যমা । যদি 2/3 AD =BC হয় , তাহলে প্রমাণ করি যে , অপর দুটি কোণের অন্তর্ভুক্ত কোণের পরিমাপ 90° ।
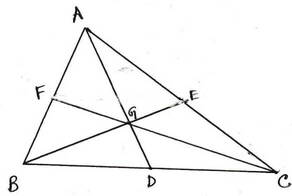
ধরি , ∆ABC এর AD ,BE এবং CF মধ্যমাত্রয় পরস্পরকে G বিন্দুতে ছেদ করেছে এবং 2/3 AD = BC । প্রমাণ করতে হবে যে ,অপর দুটি মধ্যমা BE এবং CF এর অন্তর্ভুক্ত কোণ ∠BGC = 90º
প্রমাণঃ যেহেতু , ∆ABC এর ভরকেন্দ্র G

∴ DG = ½ BC —(i)
আবার যেহেতু D ,BC –এর মধ্যবিন্দু
∴ BD =DC = ½ BC —(ii)
(i) ও (ii) থেকে পাই ,
∴ DG =BD = DC
এখন ∆BGD এর BD = DG
∴ ∠DBG =∠DGB
এবং ∆CGD এর CD = DG
∴ ∠DCG = ∠DGC
যেহেতু , ত্রিভুজের তিনটি কোণের সমষ্টি 180º
∴ ∆BGD থেকে পাই ,
∠DBG + ∠DGB + ∠BDG = 180º —(iii)
এবং ∆CGD থেকে পাই ,
∠DCG + ∠DGC +∠CDG = 180º —(iv)
(iii) ও (iv) নং সমীকরণ থেকে পাই ,
∠DBG +∠DGB +∠BDG +∠DCG +∠DGC+ ∠CDG = 180º +180º
বা, 2∠DGB +∠BDG +2∠DGC + ∠CDG = 360º
বা, 2(∠DGB + ∠DGC) + ∠BDG + ∠CDG =360º
∵ BC বাহুর ওপর DG দন্ডায়মান ।
∴ ∠BDG +∠CDG = 180º
∴ 2(∠DGB + ∠DGC) + 180º = 360º
বা, 2∠BGC = 180º
বা, ∠BGC = 90º
∴ ∠BGC = 90º [ প্রমাণিত ]
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
9. ABCD সামান্তরিকের BC ও CD বাহুর মধ্যবিন্দু যথাক্রমে P এবং Q ; AP এবং AQ কর্ণ BD –কে যথাক্রমে K ও L বিন্দুতে ছেদ করে । প্রমাণ করি যে , BK =KL = LD
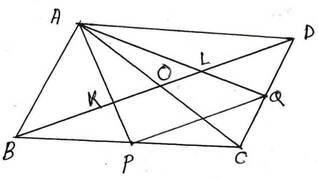
ধরি , ABCD সামান্তরিকের BC এবং CD বাহুর মধ্যবিন্দু যথাক্রমে P এবং Q ; AP এবং AQ কর্ণ BD –কে যথাক্রমে K ও L বিন্দুতে ছেদ করে । প্রমাণ করতে হবে যে , BK = KL = LD
অঙ্কনঃ A ,C যুক্ত করলাম ।
প্রমাণঃ যেহেতু সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে । ∴ O , AC এর মধ্যবিন্দু এবং OB = OD
এখন ∆ABC –এর AC এবং BC বাহুর মধ্যবিন্দু যথাক্রমে O এবং P
∴ ∆ABC এর AP এবং BO মধ্যমা পরস্পরকে K বিন্দুতে ছেদ করেছে ।
∴ K , ∆ABC এর ভরকেন্দ্র ।

∴ BK = KL =LD [প্রমাণিত ]
| WBBSE Class 9 Math Koshe Dekhi 17|সমবিন্দু সংক্রান্ত উপপাদ্য কষে দেখি ১৭|Ganit Prakash Class 9 Solution Of Chapter 17|Ganit Prakash Class Nine Solution Koshe Dekhi 17|West Bengal Board Class Nine Math Book Solution| গণিত প্রকাশ নবম শ্রেণি কষে দেখি ১৭ সমাধান |গণিত প্রকাশ ক্লাস ৯ কষে দেখি ১৭ সমবিন্দু সংক্রান্ত উপপাদ্য সমাধান |
10. বহু বিকল্পীয় প্রশ্ন (M.C.Q):
(i) ABC ত্রিভুজের পরিকেন্দ্র O ; ∠BOC = 80° হলে, ∠BAC এর পরিমাপ
(a ) 40°
(b ) 160°
(c ) 130°
(d) 110°
Ans: (a ) 40°
সমাধানঃ
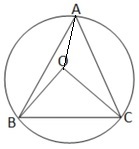
ABC ত্রিভুজের পরিকেন্দ্র O
∴ OA = OB = OC [একই বৃত্তের ব্যাসার্ধ ]
∴ ∠OBC = ∠OCB = (180º-∠BOC)/2 = (180º- 80º)/2 = 100º/2 =50º
ধরি , ∠OAB =∠OBA = x এবং ∠OAC = ∠OCA = y
এখন , ABC ত্রিভুজ থেকে পাই ,
∠A +∠B +∠C = 180º
বা, ∠OAB +∠OAC +∠OBA+ ∠OBC + ∠OCB +∠OCA = 180º
বা, x+y +x+50º + 50º + y = 180º
বা, 2x+2y +100º = 180º
বা, 2(x+y) = 180º-100º
বা, x+y = 80º/2
বা, x+y = 40º
∴ ∠BAC = 40º
বিকল্প পদ্ধতিঃ ABC ত্রিভুজের পরিকেন্দ্র O হলে , ∠BOC = 2∠BAC [যেহেতু , একই বৃত্তচাপের ওপর কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন ]
∴ ∠BAC = ½ ∠BOC = ½ ☓ 80° = 40°
(ii) ABC ত্রিভুজের লম্ববিন্দু O ; ∠BAC = 40° হলে ∠BOC এর পরিমাপ –
(a) 80°
(b) 140°
(c ) 110°
(d ) 40°
Ans: (b) 140°
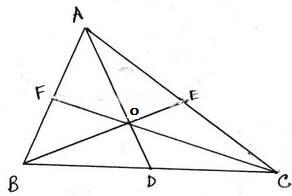
সমাধানঃ চতুর্ভুজ AFOE –এর ∠FAE = ∠BAC = 40°
এবং ∠OFA = ∠OEA =90°
∠FOE = 360° –(∠FAE + ∠OFA +∠OEA)
= 360° –(40°+90°+90°)
= 360°- 220°
= 140°
iii) ABC ত্রিভুজের অন্তকেন্দ্র O ; ∠BAC = 40° হলে ∠BOC –এর পরিমাপ
(a ) 80°
(b) 110°
(c ) 140°
(d) 40°
Ans: (b) 110°

সমাধানঃ ABC ত্রিভুজের অন্তঃকেন্দ্র O ।
∴ OA ,OB এবং OC যথাক্রমে A ,B এবং C –এর সমদ্বিখন্ডক ।
∆ABC –এর ∠ABC +∠ACB +∠BAC =180º
বা, 2∠OBC +2∠OCB + 40º = 180º
বা, 2(∠OBC +∠OCB ) = 180º-40º
বা, 2(∠OBC +∠OCB) = 140º
বা, ∠OBC +∠OCB = 140º /2
বা, ∠OBC +∠OCB = 70º
এখন OBC ত্রিভুজ থেকে পাই ,
∠BOC = 180º –(∠OBC +∠OCB ) = 180º – 70º = 110º
(iv) ABC ত্রিভুজের ভরকেন্দ্র G ; GBC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল 12 বর্গ সেমি. হলে ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল
(a) 24 বর্গ সেমি.
(b) 6 বর্গ সেমি.
(c ) 36 বর্গ সেমি.
(d ) কোনোটিই নয় ।
Ans: (c ) 36 বর্গ সেমি.

সমাধানঃ ∆ABC এর ক্ষেত্রফল =3 ☓ ∆BGC –এর ক্ষেত্রফল = 3 ☓ 12 বর্গ সেমি. = 36 বর্গ সেমি. ।
(v) ABC সমকোণী ত্রিভুজের পরিব্যাসার্ধের দৈর্ঘ্য 5 সেমি. হলে অতিভুজের দৈর্ঘ্য
(a ) 25 সেমি.
(b) 10 সেমি.
(c ) 5 সেমি.
(d) কোনোটিই নয় ।
Ans:(b) 10 সেমি.
সমাধানঃ সমকোণী ত্রিভুজের পরিব্যাসার্ধের দৈর্ঘ্য তার অতিভুজের দৈর্ঘ্যের অর্ধেক ।
∴ সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য = 2☓5 সেমি. = 10 সেমি. ।
11. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ
(i) একটি ত্রিভুজের বাহুর বাহুর দৈর্ঘ্য 6 সেমি. , 8 সেমি. ও 10 সেমি. হলে ত্রিভুজটির পরিকেন্দ্র ত্রিভুজাকার ক্ষেত্রের কোথায় অবস্থিত তা লিখি ।
সমাধানঃ একটি ত্রিভুজের বাহুর বাহুর দৈর্ঘ্য 6 সেমি. , 8 সেমি. ও 10 সেমি. ।
এখন , 82 + 62 = 64 +36 = 100 =(10)2
∴ ত্রিভুজটি একটি সমকোণী ত্রিভুজ । আমরা জানি সমকোণী ত্রিভুজের ক্ষেত্রে ত্রিভুজের পরিকেন্দ্র ত্রিভুজটির অতিভুজের মধ্যবিন্দুতে অবস্থিত ।
∴ ত্রিভুজটির পরিকেন্দ্র ত্রিভুজাকার ক্ষেত্রের 10 সেমি. বাহুর মধ্যবিন্দুতে অবস্থিত ।
(ii) ABC সমবাহু ত্রিভুজের AD মধ্যমা এবং G ভরকেন্দ্র । ত্রিভুজটির বাহুর দৈর্ঘ্য 3√3 সেমি. হলে AG –এর দৈর্ঘ্য কত তা লিখি ।


(iii)একটি ত্রিভুজের কয়টি বিন্দু ত্রিভুজের বাহুগুলি থেকে সমদূরবর্তী তা লিখি ।
সমাধানঃ একটি অন্তঃকেন্দ্র (অন্তর্বৃত্তের কেন্দ্র ) এবং তিনটি বহিঃকেন্দ্র (বহিঃবৃত্তের কেন্দ্র) ত্রিভুজের বাহুগুলি থেকে সমদূরবর্তী ।
∴ একটি ত্রিভুজের চারটি বিন্দু ত্রিভুজের বাহু গুলি থেকে সমদূরবর্তী ।
(iv) ABC সমবাহু ত্রিভুজের পাদ ত্রিভুজ ∆DEF ; ∆FDA এর পরিমাপ কত তা লিখি ।

সমাধানঃ সমবাহু ত্রিভুজের পাদ ত্রিভুজও সমবাহু ত্রিভুজ হবে ।
∴ DEF একটি সমবাহু ত্রিভুজ , সুতরাং এর প্রতিটি কোণ 60º
যেহেতু AB এবং AC এর মধ্যবিন্দু যথাক্রমে F এবং E
∴ FE = ½ BC = ½ AC = ½ AB [∵ AB =BC = CA ]
∴ AEF একটি সমবাহু ত্রিভুজ , সুতরাং এর প্রতিটি কোণ 60º
∆ADF এর FD = AF
∴ ∠FDA = ∠FAD
∴ ∠FDA +∠FAD +∠AFD = 180º
বা, ∠FDA +∠FDA + [∠AFP +∠DFP ] = 180º
বা, 2∠FDA + [60º+60º] =180º
বা, 2∠FDA = 180º-120º
বা, 2∠FDA = 60º
বা, ∠FDA = 30º
∴ ∠FDA = 30º
গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন ।
(v) ABC সমদ্বিবাহু ত্রিভুজের ∠ABC = ∠ACB এবং মধ্যমা AD = ½ BC । যদি AB = √2 সেমি. হয় তাহলে ত্রিভুজটির পরিব্যাসার্ধের দৈর্ঘ্য কত তা লিখি ।

সমাধানঃ ABC সমদ্বিবাহু ত্রিভুজের D ,BC বাহু মধ্যবিন্দু এবং AD = ½ BC
∴ ∠BAC =90º ,সুতরাং , ABC একটি সমকোণী ত্রিভুজ
আবার , ABC সমদ্বিবাহু ত্রিভুজের ∠ABC = ∠ACB
∴ AB = AC = √2 সেমি.
ABC সমকোণী সমদ্বিবাহু ত্রিভুজের AB2 + AC2 = BC2

very good
Thanks 🙏🙏
Thanks sir i Reacpidt for you 🫡❤