বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.1|Koshe Dekhi 15.1 Class 10|গণিত প্রকাশ দশম শ্রেণি (ক্লাস ১০) (টেন) কষে দেখি ১৫.১ সমাধান|Theorems Related To Tangent To a Circle|WBBSE Madhyamik Ganit Prakash Class 10| WBBSE Class 10(Ten)(X) Math Solution Of Chapter 15|WB Board Class 10 Math Book Solution.
মাধ্যমিক গণিত প্রকাশ বইএর সকল অধ্যায় সমাধানের জন্য এখানে CLICK করুন
বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.1।Koshe Dekhi 15.1 Class 10|কষে দেখি 15.1 ক্লাস 10
1. মাসুম O কেন্দ্রীয় একটি বৃত্ত অঙ্কন করেছে যার AB একটি জ্যা । B বিন্দুতে একটি স্পর্শক অঙ্কন করেছি যা বর্ধিত AO –কে T বিন্দুতে ছেদ করল । ∠BAT =21º হলে , ∠BTA এর মান হিসাব করে লিখি ।
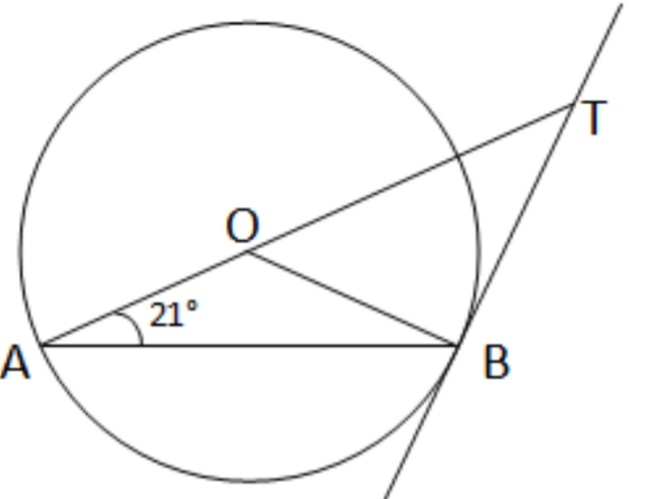
O কেন্দ্রীয় বৃত্তের AB একটি জ্যা । B বিন্দুতে একটি স্পর্শক অঙ্কন করা হয়েছে যা বর্ধিত AO কে T বিন্দুতে ছেদ করেছে , ∠BAT = 21º হলে ∠BTA এর মান নির্ণয় করতে হবে ।
OB যুক্ত করা হল ।
∠BAT = 21º ( প্রদত্ত)
∴ ∠ABT = 21º [∵OA =OB]
আবার , OB ব্যাসার্ধ এবং BT স্পর্শক
∴ ∠OBT = 90º
আবার , ∆OAB তে BOT বহিঃস্থ কোন এবং OAB , OBA দুটি অন্তঃস্থ বিপরীত কোণ
∴∠BOT = ∠OAB+∠OBA [∵ ত্রিভুজের কোনো বাহুকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোন অন্তঃস্থ বিপরীত কোণদ্বয়ের সমষ্টির সমান ]
∴ ∠BOT = 21º+21º
বা, ∠BOT = 42º
এখন ত্রিভুজ ∆BOT থেকে পাই ,
∠BTA = 180º-(∠BOT+∠OBT)=180º-(42º+90º) = 180º-132º=48º
∴ ∠BTA = 48º [উত্তর ]
বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.1।Koshe Dekhi 15.1 Class 10
2. কোনো বৃত্তের XY একটি ব্যাস । বৃত্তটির ওপর অবস্থিত A বিন্দুতে PAQ বৃত্তের স্পর্শক । x বিন্দু থেকে বৃত্তের স্পর্শকের ওপর অঙ্কিত লম্ব PAQ কে z বিন্দুতে ছেদ করেছে । প্রমান করি যে XA, ∠YXZ এর সমদ্বিখন্ডক ।
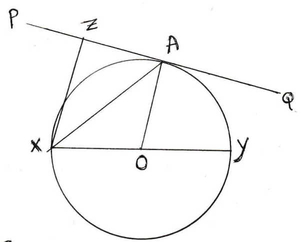
সমাধানঃ XY বৃত্তের ব্যাস । বৃত্তটির ওপর A বিন্দুতে PAQ স্পর্শক টানা হল । X বিন্দু থেকে PAQ স্পর্শক এর ওপর অঙ্কিত লম্ব স্পর্শকটিকে Z বিন্দুতে ছেদ করেছে ।XA যুক্ত করা হল , প্রমাণ করতে হবে যে , AX কোন ∠YXZ এর সমদ্বিখণ্ডক ।
অঙ্কনঃ O,A যুক্ত করা হল ।
প্রমাণঃ OA বৃত্তের ব্যাসার্ধ এবং PAQ স্পর্শক
∴ ∠OAP = 90º
∴ ∠OAX+∠XAZ = 90º—–(i)
আবার , AXZ ত্রিভুজের , AZX = 90º
∴ ∠AXZ+∠XAZ = 90º [ ∵ ত্রিভুজের তিনটি কোণের সমষ্টি 180º ]—-(i)
(i) ও (ii) নং সমীকরন তুলনা করে পাই ,
∠OAX +∠XAZ = ∠AXZ+∠XAZ
∴ ∠OAX = ∠AXZ —- (iii)
আবার , OXA এর ক্ষেত্রে ,
∠OXA = ∠OAX [∵OX=OA , একই বৃত্তের ব্যাসার্ধ ]—–(iv)
∴ (iii) ও (iv) নং সমীকরন থেকে পাই ,
∠OXA = ∠AXZ
∴ XA , ∠YXZ এর সমদ্বিখণ্ডক [ প্রমানিত ]
বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.1।Koshe Dekhi 15.1 Class 10
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
3. একটি বৃত্ত অঙ্কন করলাম যার PR একটি ব্যাস । P বিন্দুতে একটি স্পর্শক অঙ্কন করলাম এবং ওই স্পর্শকের ওপরে S এমন একটি বিন্দু নিলাম যাতে PR = PS হয় । RS , বৃত্তকে T বিন্দুতে ছেদ করলে , প্রমাণ করি যে ST =RT=PT.
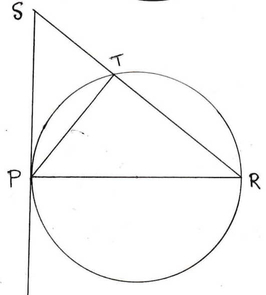
PR একটি বৃত্তের ব্যাস । P বিন্দুতে অঙ্কিত স্পর্শকের উপরে S একটি বিন্দু যাতে ,PS =PR হয় । RS বৃত্তকে T বিন্দুতে ছেদ করে , প্রমাণ করতে হবে যে , ST =RT=PT
প্রমাণঃ PR বৃত্তটির ব্যাস এবং P বিন্দুতে , PS স্পর্শক ।
∴ ∠SPR = 90º
আবার , PR =PS
∴ PSR = PRS
∴ সমকোণী ত্রিভুজ ∆PRS এর ক্ষেত্রে ,
∠SPR+∠PSR+∠PRS = 180º
বা, 90+∠PSR+∠PRS = 180º
বা, ∠PSR + ∠PRS = 180º-90º
বা, ∠PSR +∠PRS = 90º
বা, ∠PSR = ∠PRS = 45º [∵ PSR = PRS ]
∴ ∠PRT = ∠PST =45º
আবার , ∠PTR = 90º [∵ অর্ধবৃত্তস্থ কোণ 1 সমকোণ ]
∠PRT =45º
∴ ∠TPR = 180º-(∠PTR+∠PRT)
বা,∠TPR =180º-(90º+45)
বা,∠TPR= 180º-135º= 45º
বা,∠TPR =45º
এখন ∠PTR = 90º [∵অর্ধবৃত্তস্থ কোণ 1 সমকোণ ]
ত্রিভুজ ∆PTR এর, ∠PRT+∠TPR = 90º
∴∠TPR +45 =90º
বা, ∠TPR = 45º
∴ ∠TPR = ∠TRP =45º
∴PT = RT—- (i)
আবার , ∆SPT ত্রিভুজের ক্ষেত্রে ,
∠PTR = 90º [∵ অর্ধবৃত্তস্থ কোন 1 সমকোণ ]
∴ ∠STP =90º
∴ ∠PST+∠SPT = 90º
বা, 45 + ∠SPT = 90º
বা, ∠SPT = 45º
∴ ত্রিভুজ ∆SPT এর ক্ষেত্রে,
∠SPT = ∠PST = 45º
∴ PT = ST —– (ii)
∴ (i) ,(ii) থেকে পাই , ST =RT=PT [ প্রমানিত ]
বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.1।Koshe Dekhi 15.1 Class 10
4. একটি O কেন্দ্রীয় বৃত্ত অঙ্কন করি যার দুটি ব্যাসার্ধ OA ও OB পরস্পর লম্বভাবে অবস্থিত । A ও B বিন্দুতে অঙ্কিত স্পর্শকদ্বয় পরস্পরকে T বিন্দুতে ছেদ করলে , প্রমাণ করি যে ,AB =OT এবং তারা পরস্পরকে লম্বভাবে সমদ্বিখন্ডিত করে ।
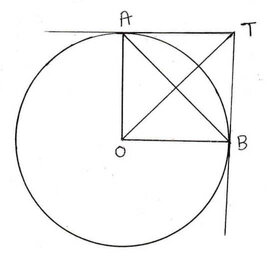
O কেন্দ্রীয় বৃত্তের OA ও OB দুটি ব্যাসার্ধ এবং তারা পরস্পর লম্ব ।A ও B বিন্দুতে অঙ্কিত স্পর্শকদ্বয় পরস্পরকে T বিন্দুতে ছেদ করে । প্রমাণ করতে হবে , AB = OT এবং AB ও OT পরস্পর লম্বভাবে অবস্থিত ।
প্রমাণঃ OA এবং OB পরস্পর লম্বভাবে অবস্থিত ।
∴ ∠AOB = 90º
আবার , OA ব্যাসার্ধ এবং AT স্পর্শক
∴ ∠OAT = 90º
OB ব্যাসার্ধ এবং BT স্পর্শক
∴ ∠OBT = 90º
∴ AOBT চতুর্ভুজের ∠AOB = 90º , ∠OAT = 90º এবং ∠OBT = 90º
∴ ∠ATB = 360º-(∠AOB+∠OAT+∠OBT)
= 360º-(90º+90º+90º) [∵ চতুর্ভুজের চারটি কোণের সমষ্টি 360º]
= 360º-270º
= 90º
অর্থাৎ চতুর্ভুজ OATB এর প্রত্যেকটি কোন 90º
এবং OA = OB [ একই বৃত্তের ব্যাসার্ধ ]
OABT একটি বর্গক্ষেত্র
AB ও OT বর্গক্ষেত্রের কর্ণ
∴ AB =OT [∵ বর্গক্ষেত্রের কর্ণদ্বয় পরস্পর সমান ]
∴ AB ⊥ OT [ ∵ বর্গক্ষেত্রের কর্ণ পরস্পরকে সমকোণে সমদ্বিখন্ডিত করে ]
বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.1।Koshe Dekhi 15.1 Class 10
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
5.দুটি এক কেন্দ্রীয় বৃত্তের বৃহত্তরটির AB ও AC জ্যা দুটি অপর বৃত্তকে যথাক্রমে P ও Q বিন্দুতে স্পর্শ করলে , প্রমাণ করি যে , PQ = ½ BC .
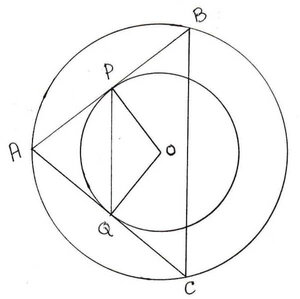
ধরাযাক , দুটি এক কেন্দ্রীয় বৃত্তের কেন্দ্র O,বৃহত্তর বৃত্তের দুটি জ্যা AB ও AC ছোট বৃত্তটিকে P ও Qবিন্দুতে স্পর্শ করেছে , প্রমাণ করতে হবে , PQ = ½ BC
অঙ্কনঃ O,P ; O ,Q যোগ করা হল ।
প্রমাণঃ OP স্পর্শবিন্দুগামী ব্যাসার্ধ ।
∴ OP ⊥ AB
∴ P বিন্দু বৃহত্তর বৃত্তের AB জ্যা-এর মধ্যবিন্দু
অনুরূপে Y বিন্দু AC জ্যা-এর মধ্যবিন্দু
∴ ত্রিভুজ ∆ABC এর AB ও AC এর মধ্যবিন্দু দুটি যথাক্রমে X ও Y
∴ XY ∥ BC এবং XY = ½ BC [ মধ্যবিন্দু সংক্রান্ত উপপাদ্য অনুসারে ]
∴ PQ = ½ BC [ প্রমানিত ]
বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.1।Koshe Dekhi 15.1 Class 10
6. O কেন্দ্রীয় বৃত্তের উপর অবস্থিত A বিন্দুতে স্পর্শকের উপর X যেকোনো একটি বিন্দু । x বিন্দু থেকে অঙ্কিত একটি ছেদক বৃত্তকে Y ও Z বিন্দুতে ছেদ করে । YZ এর মধ্যবিন্দু P হলে , প্রমাণ করি যে XAPO বা XAOP একটি বৃত্তস্থ চতুর্ভুজ ।
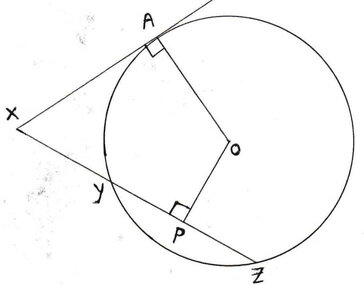
O কেন্দ্রীয় বৃত্তের উপর A একটি বিন্দু এবং A বিন্দুতে স্পর্শকের উপর X যেকোনো একটি বিন্দু , X বিন্দু দিয়ে অঙ্কিত একটি ছেদক বৃত্তটিকে Y ও Z বিন্দুতে ছেদ করে । YZ এর মধ্যবিন্দু P হলে , প্রমাণ করতে হবে যে XAOP বা XAPO একটি বৃত্তস্থ চতুর্ভুজ ।
প্রমাণঃ P , YZ এর মধ্যবিন্দু ।
এবং OP হল বৃত্তের কেন্দ্রগামী একটি সরলরেখা ।
∴ OP ⊥ YZ
∴ ∠OPX =90°
আবার , AX স্পর্শক এবং OA স্পর্শবিন্দুগামী ব্যাসার্ধ
∴ ∠OAX =90°
এখন ,XAOP চতুর্ভুজের, ∠OPX+∠OAX =90+90=180°
অর্থাৎ বিপরীত কোনগুলির সমষ্টি 2 সমকোণ
সুতরাং XAOP একটি বৃত্তস্থ চতুর্ভুজ [ প্রমানিত ]
বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.1।Koshe Dekhi 15.1 Class 10
7.O কেন্দ্রীয় কোন বৃত্তের একটি ব্যাসের উপর P যেকোনো একটি বিন্দু । ওই ব্যাসের ওপর O বিন্দুতে অঙ্কিত লম্ব বৃত্তকে Q বিন্দুতে ছেদ করে । বর্ধিত QP বৃত্তকে R বিন্দুতে ছেদ করে । R বিন্দুতে অঙ্কিত স্পর্শক বর্ধিত OP কে S বিন্দুতে ছেদ করে । প্রমাণ করি যে SP = SR ।
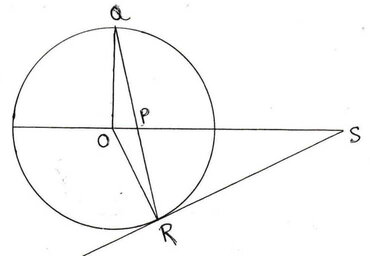
O কেন্দ্রীয় বৃত্তের একটি ব্যাসের উপর P যেকোনো একটি বিন্দু । O বিন্দুতে অঙ্কিত লম্ব Q কে ছেদ করে এবং QP বৃত্তকে R বিন্দুতে ছেদ করে আবার R বিন্দুতে অঙ্কিত স্পর্শক বর্ধিত OP কে S বিন্দুতে ছেদ করে । প্রমাণ করতে হবে যে , SP = SR
অঙ্কনঃ OR যুক্ত করা হল ।
প্রমাণঃ OPQ ত্রিভুজে ∠POQ = 90°
∴ ∠OPQ+∠OQP = 90°
বা, ∠OPQ = 90°- ∠OQP —–(i)
OQR ত্রিভুজের ক্ষেত্রে , ∠OQP = ∠ORP [ ∵ OR =OQ একই বৃত্তের ব্যাসার্ধ ]
আবার , RS স্পর্শক এবং OR স্পর্শবিন্দুগামী ব্যাসার্ধ
∴ ∠ORS = 90°
বা, ∠ORP+∠PRS = 90°
বা, ∠PRS = 90°-∠ORP
বা, ∠PRS = 90°- ∠OQP [ ∵∠OQP = ∠ORP]
বা, ∠PRS = ∠OPQ [ (i) থেকে পাই ]
বা , ∠PRS = ∠SPR [∵∠SPR = ∠OPQ পরস্পর বিপ্রতীপ কোণ ]
∴ SPR ত্রিভুজের ক্ষেত্রে , ∠SPR = ∠SRP
∴ SP =SR [প্রমানিত]
বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.1।Koshe Dekhi 15.1 Class 10
8.রুমেলা O কেন্দ্রীয় একটি বৃত্ত অঙ্কন করেছে যার QR একটি জ্যা । Q ও R বিন্দুতে দুটি স্পর্শক অঙ্কন করেছি যারা পরস্পরকে P বিন্দুতে ছেদ করেছে । QM বৃত্তের ব্যাস হলে , প্রমাণ করি যে , ∠QPR = 2 ∠RQM
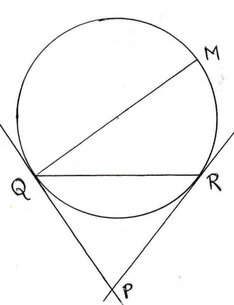
O কেন্দ্রীয় বৃত্তের QR একটি জ্যা , Q ও R বিন্দুতে অঙ্কিত স্পর্শকদুটি পরস্পরকে P বিন্দুতে ছেদ করেছে । QM বৃত্তের ব্যাস হলে, প্রমাণ করতে হবে যে , ∠QPR = 2∠RQM
প্রমাণঃ বহিঃস্থ বিন্দু P থেকে দুটি স্পর্শক PQ এবং PR অঙ্কন করা হয়েছে ।
∴ ∠PQR = ∠PRQ
∴ ∠QPR = 180°-(∠PQR+∠PRQ)
বা,∠QPR =180°-(∠PQR+∠PQR)
বা,∠QPR=180°-2∠PQR—(i)
আবার , QM বৃত্তটির ব্যাস এবং PQ স্পর্শক
∴ ∠PQM = 90° [∵স্পর্শক ও স্পর্শবিন্দুগামী ব্যাসার্ধ পরস্পর লম্ব ]
∠PQR = 90°-∠RQM —- (ii)
(i) নং সমীকরণ থেকে পাই ,
∠QPR = 180°-2∠PQR
বা,∠QPR = 180°-2(90°-∠RQM) [ (ii) নং সমীকরণ থেকে পাই]
বা,∠QPR=180°-180°+2∠RQM
বা, ∠QPR= 2∠RQM
∴ ∠QPR = 2∠RQM [প্রমানিত]
বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.1।Koshe Dekhi 15.1 Class 10
মাধ্যমিক গণিত প্রকাশ বইএর সকল অধ্যায় সমাধানের জন্য এখানে CLICK করুন
9.কোনো বৃত্তের AC ও BD জ্যা দুটি পরস্পরকে O বিন্দুতে ছেদ করেছে । A ও B বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে P বিন্দুতে এবং C ও D বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে Q বিন্দুতে ছেদ করলে , প্রমাণ করি যে , ∠P+∠Q = 2∠BOC.
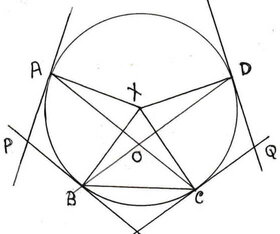
AC ও BD জ্যা দুটি পরস্পরকে O বিন্দুতে ছেদ করেছে । এখন A ও B বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে P বিন্দুতে এবং C ও D বিন্দুতে অঙ্কিত স্পর্শক দুটি পরস্পরকে Q বিন্দুতে ছেদ করে , প্রমাণ করতে হবে যে , ∠P + ∠Q = 2∠BOC
অঙ্কনঃ ধরি X হল বৃত্তের কেন্দ্র । X,A ;X,B ;X,C ;X,D এবং B,C যুক্ত করা হল ।
প্রমাণঃ APBM চতুর্ভুজের ক্ষেত্রে ,
∠MAP = 90° এবং ∠MBP =90° [ ∵ MA এবং MB প্রত্যেকে স্পর্শবিন্দুগামী ব্যাসার্ধ]
∴ ∠APB + ∠AMB = 360°-(∠MAP+∠MBP)=360°-(90°+90°)=360°-180°=180°
বা, ∠APB + ∠AMB =360°-(90°+90°)
বা,∠APB + ∠AMB=360°-180°
বা,∠APB + ∠AMB=180°
∴ ∠P+∠AMB = 180°
∵ একই বৃত্তচাপ AB এর ওপর AMB কেন্দ্রস্থ কোন এবং ACB পরিধিস্থ কোন , আবার কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন,
∴ ∠P+2∠ACB = 180°
বা, 2∠ACB = 180°-∠P —— (i)
একিভাবে প্রমান করা যায় যে ,
2∠DBC = 180°-∠Q —— (ii)
2∠ACB+2∠DBC = 180°-∠P+180-∠Q
বা, 2(∠ACB+∠DBC) = 360°-(∠P+∠Q)
বা, 2(∠OCB+∠OBC) = 360°-(∠P+∠Q)
বা, 2(180°-∠BOC) = 360°-(∠P+∠Q) [ ∆BOC এর ক্ষেত্রে , ∠BOC+∠OBC+∠OCB=180°]
বা, 360°-2∠BOC = 360°-(∠P+∠Q)
বা, 2∠BOC = (∠P+∠Q)
∴ ∠P+∠Q = 2∠BOC (প্রমানিত )
বৃত্তের স্পর্শক সংক্রান্ত উপপাদ্য কষে দেখি 15.1।Koshe Dekhi 15.1 Class 10
মাধ্যমিকের সকল বিষয়ের মক টেস্টে অংশগ্রহণ করুন এই লিঙ্কে ক্লিক করে
ধন্যবাদ । এই পোস্টটি ভাল লাগলে SHARE করার অনুরোধ রইল । এরকম আরও সুন্দর সুন্দর পোস্টের জন্য এখানে CLICK করুন ।
Good progress