Ganit Prabha Class 8 Koshe Dekhi 20.2|জ্যামিতিক প্রমাণ কষে দেখি ২০.২|গণিতপ্রভা অষ্টম শ্রেণি সমাধান|গনিতপ্রভা ক্লাস ৮ কষে দেখি ২০.২ সমাধান|WBBSE Class 8 Math Book Solution In Bengali
গনিতপ্রভা অষ্টম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
Ganit Prabha Class 8 Koshe Dekhi 20.2|জ্যামিতিক প্রমাণ কষে দেখি ২০.২|গণিতপ্রভা অষ্টম শ্রেণি সমাধান|গনিতপ্রভা ক্লাস ৮ কষে দেখি ২০.২ সমাধান|WBBSE Class 8 Math Book Solution In Bengali
1. নীচের বহুভুজগুলির অন্তঃকোণের সমষ্টি লিখি-
(i) পঞ্চভুজ (ii) ষড়ভুজ (iii) সপ্তভুজ (iv) অষ্টভুজ (v) দশভুজ (vi) বহুভুজ যার বাহুসংখ্যা 12 টি ।
সমাধানঃ
(i) n সংখ্যক বাহু বিশিষ্ট বহুভুজের অন্তঃকোণের সমষ্টি = (2n-4)সমকোণ ।
∴ পঞ্চভুজের অন্তঃকোণের সমষ্টি = {2(5) – 4} সমকোণ = {2(5) -4}✕90° = (10-4) ✕ 90° = 6✕90° = 540°
(ii) n সংখ্যক বাহু বিশিষ্ট বহুভুজের অন্তঃকোণের সমষ্টি = (2n-4)সমকোণ ।
∴ ষড়ভুজের অন্তঃকোণের সমষ্টি = {2(6) – 4} সমকোণ = {2(6) -4}✕ 90° = (12-4) ✕ 90° = 8 ✕ 90° = 720°
(iii) n সংখ্যক বাহু বিশিষ্ট বহুভুজের অন্তঃকোণের সমষ্টি = (2n-4)সমকোণ ।
∴ সপ্তভুজের অন্তঃকোণের সমষ্টি = {2(7) – 4} সমকোণ = {2(7) -4}✕ 90° = (14-4) ✕ 90° = 10 ✕ 90° = 900°
(iv) n সংখ্যক বাহু বিশিষ্ট বহুভুজের অন্তঃকোণের সমষ্টি = (2n-4)সমকোণ ।
∴ অষ্টভুজের অন্তঃকোণের সমষ্টি = {2(8) – 4} সমকোণ = {2(8) -4}✕90° = (16-4) ✕ 90° = 12 ✕ 90° = 1080°
(v) n সংখ্যক বাহু বিশিষ্ট বহুভুজের অন্তঃকোণের সমষ্টি = (2n-4)সমকোণ ।
∴ দশভুজের অন্তঃকোণের সমষ্টি = {2(10) – 4} সমকোণ = {2(10) -4}✕ 90° = (20-4) ✕ 90° = 16 ✕ 90° = 1440°
(vi) n সংখ্যক বাহু বিশিষ্ট বহুভুজের অন্তঃকোণের সমষ্টি = (2n-4)সমকোণ ।
∴ 12 টি বাহুবিশিষ্ট বহুভুজের অন্তঃকোণের সমষ্টি = {2(12) – 4} সমকোণ = {2(12) -4}✕ 90° = (24-4) ✕ 90° = 20✕90° = 1800°
2. একটি চতুর্ভুজের তিনটি কোণের পরিমাপ যথাক্রমে 104.5° , 65° এবং 72.5° চতুর্থ কোণটির মান লিখি ।
সমাধানঃ চতুর্ভুজের চারটি কোণের সমষ্টি = {2(4) – 4 }সমকোণ = (8 -4) ✕ 90° = 360°
ধরি , চতুর্থ কোণটির পরিমাপ x°
∴ 104.5° + 65° + 72.5° + x =360°
বা, 242° + x = 360°
বা, x = 360 -242
বা, x = 118 °
∴ চতুর্থ কোণটির পরিমাপ 118° ।
| Ganit Prabha Class 8 Koshe Dekhi 20.2|জ্যামিতিক প্রমাণ কষে দেখি ২০.২|গণিতপ্রভা অষ্টম শ্রেণি সমাধান|গনিতপ্রভা ক্লাস ৮ কষে দেখি ২০.২ সমাধান|WBBSE Class 8 Math Book Solution In Bengali |
3. একটি পঞ্চভুজের চারটি কোণের পরিমাপ যথাক্রমে 65° , 89° , 132° এবং 116° ; পঞ্চম কোণটির পরিমাপ লিখি ।
সমাধানঃ পঞ্চভুজের অন্তঃকোণের সমষ্টি = {2 (5) -4} সমকোণ = ( 10 -4) ✕ 90° = 540°
ধরি ,পঞ্চম কোণটির মান x
∴ 65° +89°+132° +116° +x = 540°
বা, 402° +x = 540°
বা, x = 540°-402°
বা, x = 138°
∴ পঞ্চম কোণটির মান 138°
4. একটি কুব্জ চতুর্ভুজের তিনটি কোণের পরিমাপ যথাক্রমে 68° ,70° ও 75° হতে পারে কিনা লিখি ।
সমাধানঃ চতুর্ভুজের চারটি কোণের সমষ্টি = {2(4) – 4 }সমকোণ = (8 -4) ✕ 90° = 360°
∴ চতুর্থ কোণটির পরিমাপ = {360°- ( 68°+70°+75°)} = 360° – 213° = 147° < 180°
∴ কুব্জ চতুর্ভুজের চতুর্থ কোণটির পরিমাপ 147° হতে পারে । সুতরাং একটি কুব্জচতুর্ভুজের তিনটি কোণের পরিমাপ যথাক্রমে 68° ,70° ও 75° হতে পারে ।
| Ganit Prabha Class 8 Koshe Dekhi 20.2|জ্যামিতিক প্রমাণ কষে দেখি ২০.২|গণিতপ্রভা অষ্টম শ্রেণি সমাধান|গনিতপ্রভা ক্লাস ৮ কষে দেখি ২০.২ সমাধান|WBBSE Class 8 Math Book Solution In Bengali |
5.একটি কুব্জ ষড়ভুজের পাঁচটি কোণের পরিমাপ যথাক্রমে 120° ,70° , 95° ,78° এবং 160° হতে পারে কিনা লিখি ।
সমাধানঃ ষড়ভুজের অন্তঃকোণের সমষ্টি = {2(6) – 4} সমকোণ = (12-4) ✕ 90° = 8 ✕ 90° = 720°
∴ ষড়ভুজের ষষ্ট কোণটির পরিমাপ = 720° – (120°+70°+ 95°+78°+160°) = 720° – 523° = 197° > 180°
কিন্তু কুব্জ ষড়ভুজের একটি কোণ 197° (> 180°) হতে পারে না ।
∴ ষড়ভুজের পাঁচটি অন্তঃকোণের পরিমাপ যথাক্রমে 120° ,70° , 95° ,78° এবং 160° হতে পারে না ।
6. নীচের সুষম বহুভুজের প্রতিটি অন্তঃকোণ ও প্রতিটি বহিঃকোণের পরিমাপ লিখি ।
(i) পঞ্চভুজ (ii) ষড়ভুজ (iii) অষ্টভুজ (iv) বহুভুজের বাহুসংখ্যা 9 টি (v) বহুভুজের বাহুসংখ্যা 10 টি (vi) বহুভুজের বাহুসংখ্যা 18 টি ।
সমাধানঃ n সংখ্যক বাহু বিশিষ্ট বহুভুজের অন্তঃকোণের সমষ্টি = (2n-4)সমকোণ ।
∴ সুষম পঞ্চভুজের অন্তঃকোণের সমষ্টি = {2(5) – 4} সমকোণ = (10-4) ✕ 90° = 6✕90° = 540°
∴ সুষম পঞ্চভুজের প্রতিটি অন্তকোণ = 540° /5 = 108°
এখন , প্রতিটি অন্তঃকোণ + প্রতিটি বহিঃকোণ = 180°
বা, 108° + প্রতিটি বহিঃকোণ = 180°
বা, প্রতিটি বহিঃকোণ = 180 -108
বা, প্রতিটি বহিঃকোণ = 72°
∴ প্রতিটি বহিঃকোণ = 72°
(ii) n সংখ্যক বাহু বিশিষ্ট বহুভুজের অন্তঃকোণের সমষ্টি = (2n-4)সমকোণ ।
∴ সুষম ষড়ভুজের অন্তঃকোণের সমষ্টি = {2(6) – 4} সমকোণ = (12-4) ✕90° = 8✕90° = 720°
∴ সুষম পঞ্চভুজের প্রতিটি অন্তকোণ = 720° /6 = 120°
এখন , প্রতিটি অন্তঃকোণ + প্রতিটি বহিঃকোণ = 180°
বা, 120° + প্রতিটি বহিঃকোণ = 180°
বা, প্রতিটি বহিঃকোণ = 180° -120°
বা, প্রতিটি বহিঃকোণ = 60°
∴ প্রতিটি বহিঃকোণ = 60°
(iii) n সংখ্যক বাহু বিশিষ্ট বহুভুজের অন্তঃকোণের সমষ্টি = (2n-4)সমকোণ ।
∴ সুষম অষ্টভুজের অন্তঃকোণের সমষ্টি = {2(8) – 4} সমকোণ = (16-4) ✕ 90° = 12✕90° = 1080°
∴ সুষম অষ্টভুজের প্রতিটি অন্তকোণ = 1080° /8 = 135°
এখন , প্রতিটি অন্তঃকোণ + প্রতিটি বহিঃকোণ = 180°
বা, 135° + প্রতিটি বহিঃকোণ = 180°
বা, প্রতিটি বহিঃকোণ = 180° -135°
বা, প্রতিটি বহিঃকোণ = 45°
∴ প্রতিটি বহিঃকোণ = 45°
(iv) n সংখ্যক বাহু বিশিষ্ট বহুভুজের অন্তঃকোণের সমষ্টি = (2n-4)সমকোণ ।
∴ যে বহুভুজের বাহুসংখ্যা 9 তার অন্তঃকোণের সমষ্টি = {2(9) – 4} সমকোণ = (18-4) ✕90° = 14✕90° = 1260°
∴ যে বহুভুজের বাহুসংখ্যা 9 তার প্রতিটি অন্তঃকোণ = 1260° /9 = 140°
এখন , প্রতিটি অন্তঃকোণ + প্রতিটি বহিঃকোণ = 180°
বা, 140° + প্রতিটি বহিঃকোণ = 180°
বা, প্রতিটি বহিঃকোণ = 180° -140°
বা, প্রতিটি বহিঃকোণ = 40°
∴ প্রতিটি বহিঃকোণ = 40°
(v)n সংখ্যক বাহু বিশিষ্ট বহুভুজের অন্তঃকোণের সমষ্টি = (2n-4)সমকোণ ।
∴ যে বহুভুজের বাহুসংখ্যা 10 তার অন্তঃকোণের সমষ্টি = {2(10) – 4} সমকোণ = (20-4)✕90° = 16 ✕ 90° = 1440°
∴ যে বহুভুজের বাহুসংখ্যা 10 তার প্রতিটি অন্তঃকোণ = 1440° /10 = 144°
এখন , প্রতিটি অন্তঃকোণ + প্রতিটি বহিঃকোণ = 180°
বা, 144° + প্রতিটি বহিঃকোণ = 180°
বা, প্রতিটি বহিঃকোণ = 180° -144°
বা, প্রতিটি বহিঃকোণ = 36°
∴ প্রতিটি বহিঃকোণ = 36°
(vi) n সংখ্যক বাহু বিশিষ্ট বহুভুজের অন্তঃকোণের সমষ্টি = (2n-4)সমকোণ ।
∴ যে বহুভুজের বাহুসংখ্যা 18 তার অন্তঃকোণের সমষ্টি = {2(18) – 4} সমকোণ = (36-4) ✕ 90° = 32✕90° = 2880°
∴ যে বহুভুজের বাহুসংখ্যা 18 তার প্রতিটি অন্তঃকোণ = 2880° /18 = 160°
এখন , প্রতিটি অন্তঃকোণ + প্রতিটি বহিঃকোণ = 180°
বা, 160° + প্রতিটি বহিঃকোণ = 180°
বা, প্রতিটি বহিঃকোণ = 180° -160°
বা, প্রতিটি বহিঃকোণ = 20°
∴ প্রতিটি বহিঃকোণ = 20°
| Ganit Prabha Class 8 Koshe Dekhi 20.2|জ্যামিতিক প্রমাণ কষে দেখি ২০.২|গণিতপ্রভা অষ্টম শ্রেণি সমাধান|গনিতপ্রভা ক্লাস ৮ কষে দেখি ২০.২ সমাধান|WBBSE Class 8 Math Book Solution In Bengali |
7. একটি সুষম বহুভুজের প্রতিটি বহিঃকোণের পরিমাপ নিম্নলিখিত পরিমাপ গুলি হতে পারে কিনা ( হ্যাঁ / না ) লিখি ।
(i) 6° (ii) 10° (iii) 13° (iv) 18° (v) 35°
সমাধানঃ
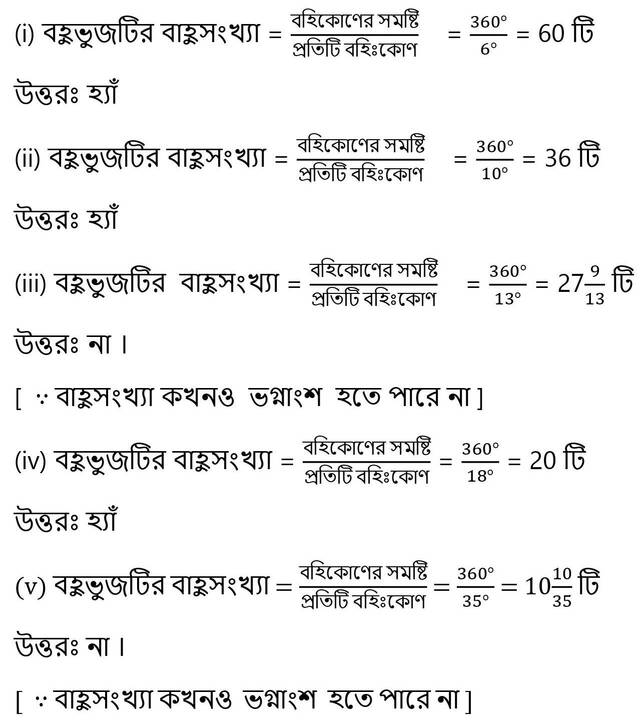
8. একটি সুষম বহুভুজের প্রতিটি অন্তঃকোণের পরিমাপ নিম্নলিখিত পরিমাপগুলি হতে পারে কিনা (হ্যাঁ / না) লিখি ।
(i) 80° (ii) 100° (iii) 120° (iv) 144° (v) 155° (vi) 160°
সমাধানঃ
(i) একটি অন্তঃকোণের পরিমাপ 80°
এখন , একটি অন্তঃকোণ + একটি বহিঃকোণ = 180°
বা, 80° + একটি বহিঃকোণ = 180°
বা, একটি বহিঃকোণ = 180°-80°
বা, একটি বহিঃকোণ = 100°
বহুভুজটির বাহুসংখ্যা = বহিঃকোণের সমষ্টি / একটি বহিঃকোণ = 360° / 100° = 3.6
উত্তরঃ না ।
[ ∵ বহুভুজের বাহুসংখ্যা কখনও দশমিক ভগ্নাংশে হতে পারে না ]
(ii) একটি অন্তঃকোণের পরিমাপ 100°
এখন , একটি অন্তঃকোণ + একটি বহিঃকোণ = 180°
বা, 100° + একটি বহিঃকোণ = 180°
বা, একটি বহিঃকোণ = 180°-100°
বা, একটি বহিঃকোণ = 80°
বহুভুজটির বাহুসংখ্যা = বহিঃকোণের সমষ্টি / একটি বহিঃকোণ = 360° / 80° = 4.5
উত্তরঃ না ।
[ ∵ বহুভুজের বাহুসংখ্যা কখনও দশমিক ভগ্নাংশে হতে পারে না ]
(iii) একটি অন্তঃকোণের পরিমাপ 120°
এখন , একটি অন্তঃকোণ + একটি বহিঃকোণ = 180°
বা, 120° + একটি বহিঃকোণ = 180°
বা, একটি বহিঃকোণ = 180°-120°
বা, একটি বহিঃকোণ = 60°
বহুভুজটির বাহুসংখ্যা = বহিঃকোণের সমষ্টি / একটি বহিঃকোণ = 360° / 60° = 6
উত্তরঃ হ্যাঁ ।
(iv) একটি অন্তঃকোণের পরিমাপ 144°
এখন , একটি অন্তঃকোণ + একটি বহিঃকোণ = 180°
বা, 144° + একটি বহিঃকোণ = 180°
বা, একটি বহিঃকোণ = 180°-144°
বা, একটি বহিঃকোণ = 36°
বহুভুজটির বাহুসংখ্যা = বহিঃকোণের সমষ্টি / একটি বহিঃকোণ = 360° / 36° = 10
উত্তরঃ হ্যাঁ ।
গনিতপ্রভা অষ্টম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
(v) একটি অন্তঃকোণের পরিমাপ 155°
এখন , একটি অন্তঃকোণ + একটি বহিঃকোণ = 180°
বা, 155° + একটি বহিঃকোণ = 180°
বা, একটি বহিঃকোণ = 180°-155°
বা, একটি বহিঃকোণ = 25°
বহুভুজটির বাহুসংখ্যা = বহিঃকোণের সমষ্টি / একটি বহিঃকোণ = 360° / 25° = 14.4
উত্তরঃ না ।
[ ∵ বহুভুজের বাহুসংখ্যা কখনও দশমিক ভগ্নাংশে হতে পারে না ]
(v) একটি অন্তঃকোণের পরিমাপ 160°
এখন , একটি অন্তঃকোণ + একটি বহিঃকোণ = 180°
বা, 160° + একটি বহিঃকোণ = 180°
বা, একটি বহিঃকোণ = 180°-160°
বা, একটি বহিঃকোণ = 20°
বহুভুজটির বাহুসংখ্যা = বহিঃকোণের সমষ্টি / একটি বহিঃকোণ = 360° / 20° = 18
উত্তরঃ হ্যাঁ ।
9. একটি সুষম বহুভুজের প্রতিটি বহিঃকোণের পরিমাপ 60° ; বহুভুজটির বাহুসংখ্যা লিখি ।
সমাধানঃ সুষম বহুভুজের প্রতিটি বহিঃকোণের পরিমাপ 60°
∴ বহুভুজটির বাহুসংখ্যা = 360° / 60° = 6 টি ।
10. একটি সুষম বহুভুজের প্রতিটি অন্তঃকোণের পরিমাপ 135°; বহুভুজটির বাহুসংখ্যা লিখি ।
সমাধানঃ একটি অন্তঃকোণের পরিমাপ 135°
এখন , একটি অন্তঃকোণ + একটি বহিঃকোণ = 180°
বা, 135° + একটি বহিঃকোণ = 180°
বা, একটি বহিঃকোণ = 180°-135°
বা, একটি বহিঃ কোণ = 45°
বহুভুজটির বাহুসংখ্যা = বহিঃকোণের সমষ্টি / একটি বহিঃকোণ = 360° / 45° = 8 টি ।
11. একটি সুষম বহুভুজের প্রতিটি অন্তঃকোণ ও বহিঃকোণের পরিমানের অনুপাত 3:2 । বহুভুজটির বাহুসংখ্যা লিখি ।
সমাধানঃ ধরি , সুষম বহুভুজটির প্রতিটি অন্তঃকোণ 3x এবং প্রতিটি বহিঃকোণ 2x ।
শর্তানুসারে ,
3x+2x = 180°
বা, 5x = 180°
বা, x = 180°/5
বা, x = 36
∴ x = 36
∴ প্রতিটি অন্তকোণ = 3✕36° = 108 এবং প্রতিটি বহিঃকোণ = 2✕36° = 72°
∴ বহুভুজটির বাহুসংখ্যা = 360° / 72° = 5 টি ।
12. একটি বহুভুজের অন্তঃকোণগুলির সমষ্টি 1800° ; বহুভুজটির বাহুসংখ্যা লিখি ।
সমাধানঃ ধরি , বহুভুজটির বাহুসংখ্যা n ।
শর্তানুসারে ,
(2n-4) সমকোণ = 1800°
বা, (2n-4) ✕ 90° = 1800°
বা, (2n-4) = 1800°/90°
বা, 2n-4 = 20
বা, 2n = 20+4
বা, 2n = 24
বা, n = 24/2
বা, n =12
∴ বহুভুজটির বাহুসংখ্যা 12 টি ।
13. একটি বহুভুজের পাঁচটি অন্তঃ কোণের প্রতিটির পরিমাপ 172° এবং অপর অন্তঃকোণ গুলির প্রতিটির পরিমাপ 160° ; বহুভুজটির বাহুসংখ্যা কত ?
সমাধানঃ ধরি , বহুভুজটির বাহুসংখ্যা n টি ।
∴ বহুভুজটির অন্তঃকোণগুলির সমষ্টি = (2n-4) সমকোণ = (2n-4)✕90°
পাঁচটি অন্তঃকোণের প্রতিটির পরিমাপ = 172°
∴ পাঁচটি অন্তঃকোণের সমষ্টি = (172°✕5) = 860°
বাকি অন্তঃ কোণগুলির প্রতিটির পরিমাপ 160°
∴ বাকি অন্তঃকোণ গুলির সমষ্টি = (n-5)✕160°
শর্তানুসারে ,
860 + (n-5)✕160 = (2n-4)✕90
বা, 860+ 160n – 800 = 180n – 360
বা, 60 + 360 = 180n -160n
বা, 420 = 20n
বা, 20n = 420
বা, n = 420/20
বা, n = 21
∴ বহুভুজটির বাহুসংখ্যা 21 টি ।
| Ganit Prabha Class 8 Koshe Dekhi 20.2|জ্যামিতিক প্রমাণ কষে দেখি ২০.২|গণিতপ্রভা অষ্টম শ্রেণি সমাধান|গনিতপ্রভা ক্লাস ৮ কষে দেখি ২০.২ সমাধান|WBBSE Class 8 Math Book Solution In Bengali |
গনিতপ্রভা অষ্টম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
14. প্রমাণ করি যে , একটি চতুর্ভুজের যে কোনো দুটি সন্নিহিত কোণের সমদ্বিখন্ডকদ্বয়ের দ্বারা উৎপন্ন কোণ চতুর্ভুজের অপর কোণদ্বয়ের সমষ্টির অর্ধেক ।
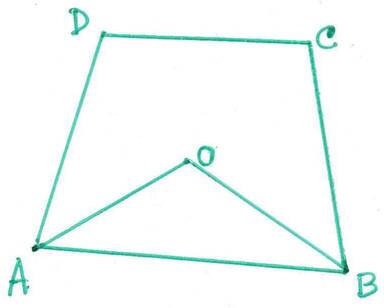
সমাধানঃ ABCD চতুর্ভুজের ∠BAD ও ∠ABC –এর অন্তঃসমদ্বিখণ্ডক AO ও BO পরস্পরকে O বিন্দুতে ছেদ করেছে । ফলে ∠AOB কোণ উৎপন্ন হল ।
প্রমাণ করতে হবে যে , ∠AOB = ½ (∠BCD + ∠ADC)
প্রমাণঃ ∠BAD –এর অন্তঃ সমদ্বিখন্ডক AO
∴ ∠BAO = ½ ∠BAD
বা, ∠BAD = 2∠BAO
∠ABC –এর অন্তঃ সমদ্বিখণ্ডক BO
∴ ∠ABO = ½ ∠ABC
বা, 2∠ABO = ∠ABC
ABCD চতুর্ভুজ থেকে পাই ,
∠BAD + ∠ABC + ∠ADC +∠BCD = 360°
বা, 2∠BAO + 2∠ABO = 360° – (∠ADC+∠BCD)
বা, 2(∠BAO +∠ABO) = 360° – (∠ADC+ ∠BCD)
বা, 2(180°-∠AOB ) = 360° – (∠ADC+ ∠BCD) [∵ AOB এর ক্ষেত্রে ∠BAO +∠ABO +∠AOB =180° ]
বা, 360° – 2∠AOB = 360° – (∠ADC+ ∠BCD)
বা, 2 ∠AOB = ∠ADC + ∠BCD
বা, ∠AOB = ½ (∠ADC+ ∠BCD) [ প্রমাণিত ]
| Ganit Prabha Class 8 Koshe Dekhi 20.2|জ্যামিতিক প্রমাণ কষে দেখি ২০.২|গণিতপ্রভা অষ্টম শ্রেণি সমাধান|গনিতপ্রভা ক্লাস ৮ কষে দেখি ২০.২ সমাধান|WBBSE Class 8 Math Book Solution In Bengali |
15.ABCDE একটি সুষম পঞ্চভুজ । প্রমাণ করি যে ABC সমদ্বিবাহু ত্রিভুজ এবং BE ও CD সমান্তরাল সরলরেখা ।
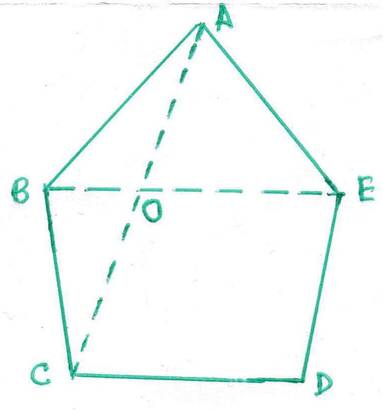
ABCDE একটি সুষম পঞ্চভুজ । AC ও BE পরস্পরকে O বিন্দুতে ছেদ করেছে । প্রমাণ করতে হবে যে , ABC একটি সমদ্বিবাহু ত্রিভুজ এবং BE || CD
প্রমাণঃ ABCDE একটি সুষম পঞ্চভুজ ।
∴ AB = BC =CD =DE =EA
∴ ABC –এর AB = AE
∴ ∆ABC একটি সমদ্বিবাহু ত্রিভুজ । [ (i) নং প্রমাণিত]
পঞ্চভুজের পাঁচটি কোণের সমষ্টি ={2(5) -4 }✕ 90° = (10-4) ✕ 90° = 6 ✕ 90° = 540°
∴ প্রতিটি অন্তঃকোণের পরিমাপ = 540 / 5 = 108°
∴ ∠ABC = ∠BCD = ∠CDE = ∠AED = ∠BAE = 108°
এখন , ∆ABE ত্রিভুজের ক্ষেত্রে , AB = AE
∴ ∠ABE = ∠AEB
∆ABE থেকে পাই ,
∠ABE + ∠AEB + ∠BAE = 180°
বা, ∠ABE +∠ABE +∠BAE = 180° [ ∵ ∠ABE = ∠AEB ]
বা, 2∠ABE +108° =180°
বা, 2∠ABE = 180° -108°
বা, 2∠ABE = 72°
বা, ∠ABE = 72°/2
বা, ∠ABE = 36°
∴ ∠EBC = ∠ABC – ∠ABE = 108° -36° = 72°
∠EBC +∠BCD = 72°+108° = 180°
এখানে , BE ও CD দুটি সরলরেখাংশ এবং BC ভেদক ।
আবার একই পাশের অন্তঃস্থ কোণ ∠EBC ও ∠BCD -এর সমষ্টি 180°
∴ BE || CD [ (ii) নং প্রমাণিত ]
| Ganit Prabha Class 8 Koshe Dekhi 20.2|জ্যামিতিক প্রমাণ কষে দেখি ২০.২|গণিতপ্রভা অষ্টম শ্রেণি সমাধান|গনিতপ্রভা ক্লাস ৮ কষে দেখি ২০.২ সমাধান|WBBSE Class 8 Math Book Solution In Bengali |
16. ABCDEF একটি সুষম ষড়ভুজ । ∠BAF –এর সমদ্বিখিন্ডক DE কে X বিন্দুতে ছেদ করে । ∠AXD -এর পরিমাপ লিখি ।
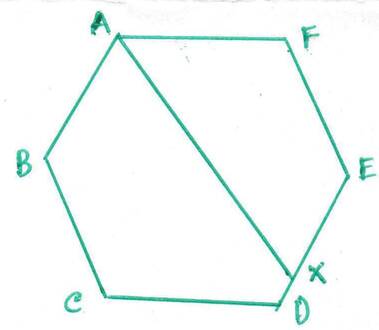
সমাধানঃ ABCDEF একটি সুষম ষড়ভুজ । ষড়ভুজের অন্তঃকোণ গুলির সমষ্টি = {2(6) -4}✕ 90° = (12-4) ✕ 90° = 8 ✕ 90° = 720°
∴ প্রতিটি অন্তঃকোণের পরিমাপ = 720° /6 = 120°
∠BAF –এর সমদ্বিখন্ডক AX
∴ ∠BAX = 120° /2 = 60°
∠ABC = ∠BCD = ∠CDX= 120° এবং ∠BAX = 60°
এখন , ABCDX পঞ্চভুজের ক্ষেত্রে ,
∠ABC + ∠BCD + ∠CDX + ∠AXD + ∠BAX = 120° +120°+ 120° +AXD + 60° = ∠AXD + 420°
পঞ্চভুজের অন্তঃকোণের সমষ্টি = {2(5) -4}✕90° = (10 -4) ✕ 90° = 6 ✕ 90° = 540°
∴ ∠AXD + 420° = 540°
বা, ∠AXD = 540°-420°
বা, ∠AXD = 120°
গনিতপ্রভা অষ্টম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন