Ganit Prabha Class 8 Koshe Dekhi 20.3|জ্যামিতিক প্রমাণ কষে দেখি ২০.৩| গণিতপ্রভা ক্লাস ৮ কষে দেখি ২০.৩ সমাধান|WBBSE Class 8 Math C hapter 20 Solution In Bengali|Ganit Prabha Class Eight Koshe dekhi 20.3 Solution
গণিতপ্রভা অষ্টম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
Ganit Prabha Class 8 Koshe Dekhi 20.3|জ্যামিতিক প্রমাণ কষে দেখি ২০.৩| গণিতপ্রভা ক্লাস ৮ কষে দেখি ২০.৩ সমাধান|WBBSE Class 8 Math C hapter 20 Solution In Bengali|Ganit Prabha Class Eight Koshe dekhi 20.3 Solution
1. দুইজন ব্যাক্তির একজন একটি পূর্ব – পশিম মুখী রাস্তায় আসার জন্য দক্ষিন দিক বরাবর আসতে শুরু করলেন এবং অপরজন একই স্থান থেকে একই সাথে দক্ষিন – পূর্ব দিকে আসতে শুরু করলেন । কোন ব্যাক্তি রাস্তায় আগে আসবেন হিসাব করে লিখি ।
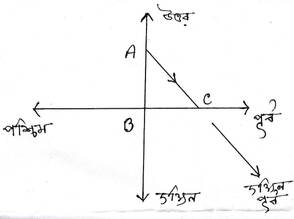
সমাধানঃ মনে করি , দুইজন ব্যাক্তি A বিন্দু থেকে পূর্ব –পশ্চিমমুখী রাস্তায় আসতে শুরু করলেন । একজন AB বরাবর দক্ষিন দিকে এবং অপরজন AC বরাবর দক্ষিন -পূর্ব দিকে আসতে শুরু করলেন । এখানে BC হল পূর্ব- পশ্চিম মুখী রাস্তা । দুজন ব্যাক্তিকে BC রাস্তায় আসতে হলে প্রথম ব্যাক্তিকে AB দুরত্ব এবং দ্বিতীয় ব্যাক্তিকে AC দুরত্ব অতিক্রম করতে হবে ।
এখানে , AB ⊥ BC
∴ ∠ABC =90°
∆ABC –এর ∠ABC > ∠ACB [ ∴ সমকোণ > সুক্ষকোণ ]
∴ AC > AB
∴ প্রথম ব্যাক্তি যিনি দক্ষিন মুখী বরাবর আসছেন তিনি আগে পূর্ব –পশ্চিম মুখী রাস্তায় আসবেন ।[প্রমাণিত ]
2. ABCD চতুর্ভুজের AB = AD এবং BC = DC ; D বিন্দু থেকে AC বাহুর ক্ষুদ্রতম দূরত্ব DP , প্রমাণ করি যে , B ,P ও D বিন্দু তিনটি সমরেখ ।
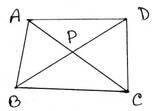
ABCD চতুর্ভুজের AB = AD এবং BC = DC । D বিন্দু থেকে AC বাহুর ক্ষুদ্রতম দুরত্ব DP । প্রমাণ করতে হবে যে , B,P ,D বিন্দু তিনটি সমরেখ ।
প্রমাণঃ ∆ABC ও ∆ADC –এর মধ্যে ,
AB = AD [ প্রদত্ত ]
BC =DC [ প্রদত্ত ]
AC সাধারণ বাহু
∴ ∆ABC ≅ ∆ADC [ সর্বসমতার s –s-s শর্তানুসারে ]
∴ ∠BAC = ∠DAC [সর্বসম ত্রিভুজের অনুরূপ কোণ ]
∆ABP এবং ∆ADP –এর মধ্যে ,
AB =AD [প্রদত্ত ]
∠BAP = ∠DAP [∵ ∠BAC =∠DAC ]
AP সাধারণ বাহু
∴ ∆ABP ≅ ∆ADP [সর্বসমতার s-s-s শর্তানুসারে ]
∴ ∠APB = ∠APD [ সর্বসম ত্রিভুজের অনুরূপ কোণ ]
D বিন্দু থেকে AC বাহুর ক্ষুদ্রতম দূরত্ব DP
∴ ∠APD = 90°
আবার , ∠APB + ∠APD = ∠APD +∠APD = 90°+90° = 180°
∴ ∠APB ও ∠APD সন্নিহিত কোণ দুটির সমষ্টি 180°
∴ B ,P ,D একই সরলরেখায় অবস্থিত । [প্রমাণিত ]
| Ganit Prabha Class 8 Koshe Dekhi 20.3|জ্যামিতিক প্রমাণ কষে দেখি ২০.৩| গণিতপ্রভা ক্লাস ৮ কষে দেখি ২০.৩ সমাধান|WBBSE Class 8 Math C hapter 20 Solution In Bengali|Ganit Prabha Class Eight Koshe dekhi 20.3 Solution |
3. ABC ত্রিভুজের AD মধ্যমা । B ও C বিন্দু থেকে AD বাহুর ক্ষুদ্রতম দূরত্ব BP ও CQ , প্রমাণ করি যে BP =CQ
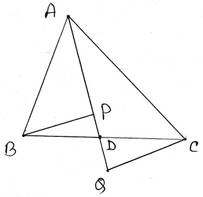
ABC ত্রিভুজের AD মধ্যমা । B ও C বিন্দু থেকে AD বাহুর ক্ষুদ্রতম দূরত্ব BP ও CQ । প্রমাণ করতে হবে যে , BP = CQ
প্রমাণঃ ABC ত্রিভুজের AD মধ্যমা ।
∴ D , BC বাহুর মধ্যবিন্দু ।
∴ BD =CD —(i)
∆BDP ও ∆CDQ –এর মধ্যে ,
∠BPD = ∠CQD
[∵ B ও C বিন্দু থেকে AD এর ওপর ক্ষুরতম দূরত্ব BP ও CQ
∴ BP ⊥ AD এবং CQ ⊥ AD ]
∠BDP = বিপ্রতীপ ∠CDQ
BD = CD [(i) নং থেকে পাই ]
∴ ∆BDP ≅ ∆CDQ [সর্বসমতার A-A-S শর্তানুসারে ]
∴ BP = CQ [সর্বসম ত্রিভুজের অনুরূপ বাহু ] [প্রমাণিত ]