Ganit Prabha Class 8 Koshe Dekhi 16.2 Solution| ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি ১৬.২

Ganit Prabha Class 8 Koshe Dekhi 16.2 Solution| ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি ১৬.২|গণিত প্রভা অষ্টম শ্রেণি (ক্লাস ৮ ) কষে দেখি ১৬.২ সমাধান |WBBSE Class 8(Eight) Math Solution Of Chapter 16 Exercise 16.2

গণিতপ্রভা অষ্টম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন	গণিত প্রকাশ নবম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
গণিত প্রকাশ দশম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন	সৌরেন্দ্রনাথ দে দ্বাদশ শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন

Ganit Prabha Class 8 Koshe Dekhi 16.2 Solution| ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি ১৬.২|গণিত প্রভা অষ্টম শ্রেণি (ক্লাস ৮ ) কষে দেখি ১৬.২ সমাধান |WBBSE Class 8(Eight) Math Solution Of Chapter 16 Exercise 16.2

কষে দেখি 16.2

1.চিত্রে ∠QPR>∠PQR PR এবং QR বাহুর সম্পর্ক লিখি ।

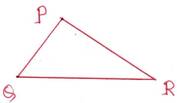
সমাধানঃ ∆ PQR  এর ∠QPR>∠PQR

যেহেতু, একটি ত্রিভুজের বৃহত্তম কোণের বিপরীত বাহুর দৈর্ঘ্য ক্ষুদ্রতর কোণটির বিপরীত বাহুর দৈর্ঘ্য অপেক্ষা বৃহত্তর।

∴ QR>PR

2. ∆ABC তে, AC>AB. AC বাহুরউপর D এমন একটি বিন্দু যে ∠ADB=∠ABD;  প্রমাণ করি যে, ∠ABC >∠ACB ।

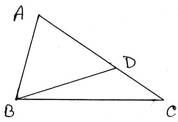
প্রদত্তঃ ∆ABC এর AC>AB , AC বাহুর উপর D এমন একটি বিন্দু যে ∠ADB=∠ABD

প্রামাণ্যঃ ∠ABC>∠ACB

প্রমাণঃ ∆ BCD এর বহিঃস্থ কোণ ∠ADB=∠CBD+∠BCD

∴ ∠ADB>∠BCD

যেহেতু, ∠ADB=∠ABD  ∴ ∠ABD >∠BCD —-(i)

আবার , ∠ABC=∠ABD+∠CBD

বা, ∠ABC > ∠ABD —-(ii)

(i) নং ও (ii) নং থেকেপাই,

∠ABC >∠BCD

∴ ∠ABC>∠ACD [প্রমাণিত]

Ganit Prabha Class 8 Koshe Dekhi 16.2 Solution| ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি ১৬.২

3. ABC ত্রিভুজের AB>AC; ∠BAC এর সমদ্বিখণ্ডক BC বাহুকে D বিন্দুতে ছেদ করে ।  প্রমাণ করি যে, BD > CD ।

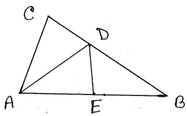
প্রদত্তঃ ABC ত্রিভুজে AB>AC; ∠BAC এর সমদ্বিখণ্ডক BC বাহুকে D বিন্দুতে ছেদ করে । অর্থাৎ ∠BAD=∠CAD

প্রামাণ্যঃ BD>CD

অঙ্কনঃ AC এর সমান করে AB বাহু থেকে AE অংশ কেটে নিলাম ।

প্রমাণঃ ∆ACD এবং ∆AED এর মধ্যে ,

AC=AE [অঙ্কনানুসারে]

∠EAD=∠CAD [যেহেতু,∠BAD=∠CAD]

AD সাধারণ বাহু

∴ ∆ACD ≅ ∆AED [সর্বসমতার S-A-S শর্তানুসারে]

∴ ∠ADC =∠ADE [সর্বসম ত্রিভুজের অনুরূপ কোণ]

এবং DE=CD [সর্বসম ত্রিভুজের অনুরূপ বাহু] —-(i)

∆ABD এর বহিঃস্থ কোণ ∠ADC > ∠ABD

∴ ∠ADE>∠ABD —-(ii)

∆AED এর বহিঃস্থ কোণ ∠BED=∠ADE —–(iii)

(ii)নং ও (iii) নং থেকে পাই,

∠BED>∠ABD                

∴ ∠BED>∠EBD

যেহেতু, একটি ত্রিভুজের বৃহত্তম  কোণের বিপরীত বাহুর দৈর্ঘ্য ক্ষুদ্রতর কোণটির বিপরীত বাহুর দৈর্ঘ্য অপেক্ষা বৃহত্তর । 

∴ BD>ED

∴ BD>CD [(1)নং থেকে পাই] [প্রমাণিত ]

4. ABC ত্রিভুজের AD, BC বাহুর উপর লম্ব এবং AC>AB; প্রমাণ করি যে, (i) ∠CAD>∠BAD (ii) DC>BD

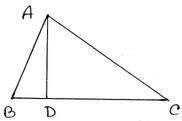
প্রদত্তঃ ABC ত্রিভুজের AD, BC বাহুর উপর লম্ব এবং AC>AB

প্রামাণ্যঃ (i) ∠CAD>∠BAD (ii) DC>BD

প্রমাণঃ যেহেতু, AD ⊥ BC

∴ ∆ACD এবং ∆ADB উভয়েই সমকোণী ত্রিভুজ

ADC সমকোণী ত্রিভুজ থেকে পাই,

∠ACD+∠CAD=90⁰  ——(1)

ADB সমকোণী ত্রিভুজ থেকে পাই,

∠ABD+∠BAD=90⁰ ——(2)

ABC ত্রিভুজের AC>AB

∴ ∠ABC>∠ACB

বা, ∠ABD>∠ACD

(1)নং ও (2) নং থেকে পাই,

∠ACD+∠CAD=∠ABD+∠BAD

যেহেতু, ∠ABD>∠ACD

∴ ∠CAD>∠BAD [(i) নং প্রমাণিত]

যেহেতু, বৃহত্তর কোণের বিপরীত বাহু > ক্ষুদ্রতর কোণের বিপরীত বাহু

 ∴ DC> BD [(ii) নং প্রমাণিত]

Ganit Prabha Class 8 Koshe Dekhi 16.2 Solution| ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি ১৬.২

5. একটি চতুর্ভুজের বৃহত্তম ও ক্ষুদ্রতম বাহু দুটির বিপরীত । প্রমান করি যে, বৃহত্তম বাহুর সন্নিহিত একটি কোণ তার বিপরীত কোণের চেয়ে ছোটো ।

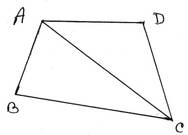
প্রদত্তঃ ABCD চতুর্ভুজের বৃহত্তম বাহু BC এবং ক্ষুদ্রতম বাহু AD পরস্পর বিপরীত বাহু ।

প্রামাণ্যঃ ∠BCD < ∠BAD

অঙ্কনঃ AC কর্ণ অঙ্কন করা হল ।

প্রমাণঃ ABCD চতুর্ভুজের বৃহত্তম বাহু BC      ∴ AB<BC

∆ABC এর AB<BC, ∴ ∠ACB < ∠BAC —– (1)

ABCD চতুর্ভুজের ক্ষুদ্রতম বাহু AD      

∴ AD<DC

∆ADC এর AD<DC, ∴ ∠ACD< ∠CAD —–(2)

(1) নং ও (ii) নং যোগ করে পাই ,

∠ACB+∠ACD< ∠BAC+∠CAD

∴ ∠BCD < ∠BAD [প্রমাণিত]

6. চিত্রে, AB<OB এবং CD>OD; প্রমান করি যে, ∠BAO>∠OCD

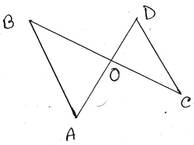
প্রমাণঃ ∆AOB এর AB<OB ∴ ∠AOB < ∠BAO —-(i)

∆COD এর CD > OD ∴ ∠COD>∠OCD —–(ii)

আবার, ∠AOB= বিপ্রতীপ ∠COD

(i) নং থেকে পাই, ∠COD < ∠BAO —-(iii)

(ii) নং ও (iii) নং থেকে পাই,

∠BAO>∠COD>∠OCD

∴ ∠BAO >∠OCD [প্রমাণিত]

7. ∆PQR এর PQ>PR; PQ বাহু থেকে PR বাহুর দৈর্ঘ্যর সমান করে PS সরলেরাখাংশ কেটে নিলাম। R এবং S বিন্দু দুটি যুক্ত করলাম । প্রমান করি যে,

(i) ∠PSR= (∠PQR+∠PRQ)

(ii) ∠QRS= (∠PRQ – ∠PQR)

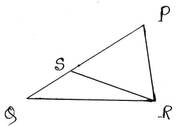
প্রদত্তঃ ∆PQR এর PQ>PR; PQ বাহু থেকে PR বাহুর দৈর্ঘ্যর সমান করে PS সরলরেখাংশ কেটে নিলাম। R এবং S বিন্দু দুটি যুক্ত করলাম ।

প্রামাণ্যঃ  (i) ∠PSR= (∠PQR+∠PRQ)

(ii) ∠QSR= (∠PRQ+∠PQR)

প্রমাণঃ  ∆PQR এর PR=PS    ∴ ∠PSR = ∠PRS

(i)∆QSR ত্রিভুজ এর বহিঃস্থ কোণ ∠PSR=∠SQR+∠SRQ

বা, ∠PSR=∠PQR+∠PRQ-∠PRS

বা, ∠PSR=∠PQR+∠PRQ-∠PSR [∵ ∠PSR = ∠PRS ]

বা, ∠PSR+∠PSR=∠PQR+∠PRQ

বা, 2∠PSR =∠PQR+∠PRQ

∴ ∠PSR= ½ (∠PQR+∠PRQ) [প্রমাণিত]

(ii) ∆QSR ত্রিভুজ এর বহিঃস্থ কোণ ∠PSR=∠SQR+∠QRS

বা, ∠QRS=∠PSR-∠SQR

বা, ∠QRS=∠PRS-∠PQR

বা, ∠QRS=∠PRQ-∠QRS-∠PQR

বা, ∠QRS+∠QRS =∠PRQ-∠PQR

বা, 2∠QRS =∠PRQ-∠PQR

∴ ∠QSR= ½(∠PRQ – ∠PQR) [প্রমাণিত]

8. ABC ত্রিভুজে, AB>AC; ∠BAC এর সমদ্বিখণ্ডক BC বাহুকে D বিন্দুতে ছেদ করে । AB বাহু থেকে AC এর দৈর্ঘ্যর সমান করে AE সরলেরাখাংশ কেটে নিলাম । D,E যুক্ত করলাম ।  প্রমাণ করি যে, (i) ∆ACD ≅ ∆AED (ii) ∠ACB>∠ABC

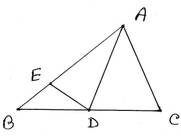
প্রদত্তঃ ABC ত্রিভুজে, AB>AC ∠BAC এর সমদ্বিখণ্ডক BC বাহুকে D বিন্দুতে ছেদ করে । AE=AC

প্রামাণ্যঃ (i) ∆ACD ≅ ∆AED (ii) ∠ACB>∠ABC

প্রমাণঃ  ∆ACD এবং ∆AED এর মধ্যে

AE=AC [প্রদত্ত]

∠DAE=∠DAC [AD, ∠BAC এর সমদ্বিখণ্ডক]

AD সাধারণ বাহু

∴ ∆ACD ≅ ∆AED [সর্বসমতার S-A-S শর্তানুসারে][(i) নং প্রমাণিত]

∴ ∠AED=∠ACD [সর্বসম ত্রিভুজের অনুরূপ কোণ]

∆BED এর বহিস্থ কোণ ∠AED=∠EBD+∠BDE

∴ ∠ACD=∠EBD+∠BDE

বা, ∠ACB=∠ABC+∠BDE [∵∠ABC=∠EBD এবং ∠ACB=∠ACD]

∴ ∠ACB>∠ABC [(ii) নং প্রমাণিত]

Ganit Prabha Class 8 Koshe Dekhi 16.2 Solution| ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি ১৬.২

9. চিত্রে, AB=CD, ∠OCD>∠COD ∠OAB<∠AOB প্রমাণ করি যে, OB<OD

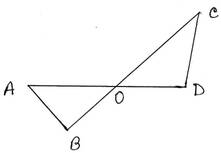
প্রমাণঃ ∆OCD এর ∠OCD>∠COD , ∴  OD>CD —-(1)

∆AOB এর ∠OAB < ∠AOB , ∴ OB < AB

∵ AB=CD , ∴ OB < CD ——- (2)

(1) নং ও (2) নং থেকে পাই,

OB<CD<OD

∴  OB < OD [প্রমাণিত]

10. প্রমান করি যে, সমকোণী ত্রিভুজের অতিভুজ বৃহত্তম বাহু ।

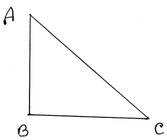
প্রদত্তঃ   ABC সমকোণী ত্রিভুজের ∠B সমকোণ এবং অতিভুজ AC ।

প্রামাণ্যঃ  অতিভুজ AC হল বৃহত্তম বাহু । অর্থাৎ AC>AB এবং AC>BC

প্রমাণঃ      ABC সমকোণী ত্রিভুজের  

∠B>∠A [∵সমকোণ >সুক্ষকোণ]

∴ AC>BC

আবার, ∠B>∠C [∵সমকোণ >সুক্ষকোণ]

∴ AC>AB

∴ AC>AB এবং AC>BC

সুতরাং, অতিভুজ AC হল বৃহত্তম বাহু ।

11. প্রমাণ করি যে, স্থূলকোণী বিপরীত বাহু বৃহত্তম ।

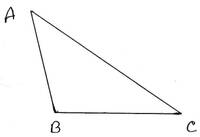
প্রদত্তঃ ABC স্থূলকোণী ত্রিভুজের ∠B স্থূলকোণ । স্থূলকোণের বিপরীত বাহু AC ।

প্রামাণ্যঃ  AC হল বৃহত্তম বাহু ।অর্থাৎ, AC>AB এবং AC>BC

প্রমাণঃ ABC স্থূলকোণী ত্রিভুজের

∠B > ∠A  [∵স্থূলকোণ >সুক্ষকোণ]

∴ AC >AB

∴ AC>AB

আবার , ∠B > ∠C [∵স্থূলকোণ >সুক্ষকোণ]

∴ AC > AB

∴ AC > AB এবং AC>BC

সুতরাং, AC হল বৃহত্তম বাহু । [প্রমাণিত ]

Ganit Prabha Class 8 Koshe Dekhi 16.2 Solution| ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি ১৬.২

12. ABC ত্রিভুজের ∠ABC ও ∠ACB এর সমদ্বিখণ্ডদ্বয় I বিন্দুতে মিলিত হয় । যদি AB > AC হয় , তবে প্রমাণ করি যে , IB > IC

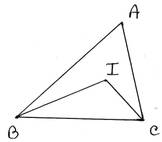
প্রদত্তঃ ABC ত্রিভুজের ∠ABC ও ∠ACB -এর সমদ্বিখন্ডকদ্বয় I বিন্দুতে মিলিত হয় এবং AB>AC

প্রামাণ্যঃ  IB>IC

প্রমাণঃ ABC ত্রিভুজের AB>AC

∴ ∠ACB>∠ABC —— (1)

BI, ∠ABC এর সমদ্বিখণ্ডক ,  ∴ ∠ABC=2∠IBC

CI, ∠ACB এর সমদ্বিখণ্ডক ,  ∴ ∠ACB=2∠ICB

(1)নং থেকে পাই,

2∠ICB>2∠IBC

বা, ∠ICB>∠IBC

∴IB>IC [প্রমাণিত]

Ganit Prabha Class 8 Koshe Dekhi 16.2 Solution| ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি ১৬.২

WBBSE OFFICIAL SITE

ধন্যবাদ । এই POST টি ভালো লাগলে SHARE করার অনুরোধ রইল । এইরকম আরও সুন্দর সুন্দর POST পাওয়ার জন্য আমাদের FACEBOOK PAGE টি LIKE করুন ।