Ganit Prabha Class 8 Koshe Dekhi 16.1|ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি ১৬.১|গণিতপ্রভা অষ্টম শ্রেণি (ক্লাস ৮ )কষে দেখি ১৬.১ সমাধান|WBBSE Class Eight Math Solution Of Chapter 16 Exercise 16.1 Solution
Ganit Prabha Class 8 Koshe Dekhi 16.1|ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি ১৬.১|গণিতপ্রভা অষ্টম শ্রেণি (ক্লাস ৮ )কষে দেখি ১৬.১ সমাধান|WBBSE Class Eight Math Solution Of Chapter 16 Exercise 16.1 Solution
কষে দেখি -16.1
1.নীচের প্রতিক্ষেত্রে (X) এর মান লিখিঃ
(i)
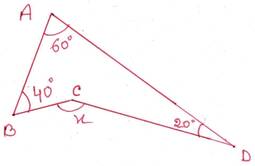
সমাধানঃ
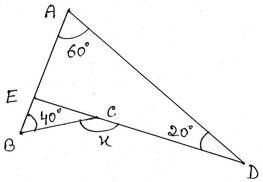
DC বাহুকে বর্ধিত করা হল যা AB বাহুকে E বিন্দুতে ছেদ করেছে ।
∆ADE এর বহিঃস্থ কোণ ∠BED
∴ ∠BED=∠DAE+∠ADE =600+200 = 800
আবার, ∆BCE এর বহিঃস্থ কোণ ∠BCD
∴ ∠BCD=∠CBE+∠BEC
=400+800 [∵∠BED=800 ∴ ∠BEC=800]
=1200
∴ x =1200
(ii)
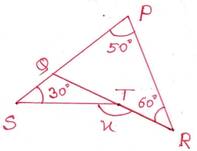
সমাধানঃ
∆PRQ এর বহিঃস্থ কোণ ∠RQS
∴ ∠RQS=∠RPQ+∠PRQ =500+500 =1100
আবার, ∆SQT এর বহিঃস্থ কোণ ∠STR
∴ ∠STR=∠TSQ+∠TQS
=300+1100 [∵∠RQS=1100 ∴ ∠TQS=1100]
=1400
∴ x=1400
(iii)
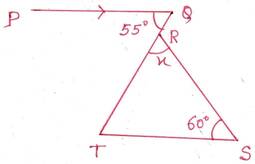
সমাধানঃ এখানে PQ||TS এবং TQ ছেদক
∴ ∠STQ= একান্তর ∠PQT =550
∆ SRT এর ∠STR=550 এবং ∠RST=600
∴ ∠SRT=1800-∠STR-∠RST=1800-550-600 =650
∴ X=650
2. পাশের চিত্রে ∆EHG এর কোণগুলির পরিমাপ লিখি ।
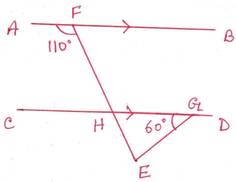
সমাধানঃ
AB||CD এবং FE ছেদক
∴ ∠CHE= অনুরূপ ∠AFH=1100
∠EHG=1800-∠CHE=1800-1100=700
∆ EHG এর ∠EHG=700 এবং ∠EGH=600
∴ ∠GEH=1800-∠EHG-∠EGH=1800-700-600 =500
∴ ∆ EHG এর ∠EHG=700, ∠EGH=600 ও ∠GEH=500
3. পাশের চিত্রে ∠A+∠B+∠C+∠D+∠E+∠F এর পরিমাপ লিখি ।
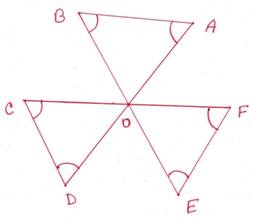
সমাধানঃ ∆AOB থেকে পাই, ∠A+∠B+ ∠AOB=1800 —-(i)
∆COD থেকে পাই, ∠C+∠D+ ∠COD=1800 —–(ii)
∆ EOF থেকে পাই, ∠E+∠F+ ∠EOF=1800 —–(iii)
∠DOE= বিপ্রতীপ ∠AOB
∠AOF= বিপ্রতীপ ∠COD
∠BOC= বিপ্রতীপ ∠EOF
O বিন্দুতে অবস্থিত সব কোণগুলির সমষ্টি 3600
∴ ∠AOB+∠BOC+∠COD+∠DOE+∠EOF+∠AOF=3600
বা, ∠AOB+∠EOF+∠COD+∠AOB+∠EOF+∠COD=3600
বা, 2(∠AOB+∠COD+∠EOF)=3600
বা, ∠AOB+∠COD+∠EOF = 1800
বা, 1800-∠A-∠B+1800 -∠C-∠D+1800-∠E-∠F= 1800 [(i) নং, (ii) নং ও (iii) নং থেকে পাই]
বা, 5400-∠A-∠B-∠C-∠D-∠E-∠F =1800
বা, -∠A-∠B-∠C-∠D-∠E-∠F =1800-5400
বা, -(∠A+∠B+∠C+∠D+∠E+∠F) =-3600
∴ ∠A+∠B+∠C+∠D+∠E+∠F =3600
Ganit Prabha Class 8 Koshe Dekhi 16.1|ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি ১৬.১
4. AB=AC হলে ∠ABC, ∠ACB ও ∠BAC এর পরিমাপ লিখি ।
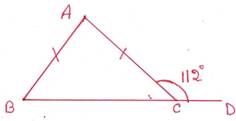
সমাধানঃ
∠ACD=1120
BD সরলরেখার উপর CA দণ্ডায়মান
∴ ∠ACB=1800-∠ACD=1800-1120=680
∆ABC এর AB=AC ∴ ∠ABC=∠ACB=680
∆ ABC এর বহিঃস্থ কোণ ∠ACD=∠ABC+∠BAC
∴ ∠BAC=∠ACD-∠ABC=1120-680=440
∴ ∠ABC=∠ACB=680 এবং ∠BAC=440
5. AB= AC হলে ∠ABC ও ∠ACB এর পরিমাপ লিখি ।
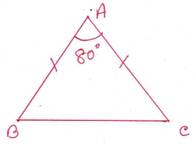
সমাধানঃ ∠BAC=800
∆ABC এর AB=AC , ∴ ∠ABC=∠ACB
∆ ABC থেকে পাই,
∠ABC+∠ACB+∠BAC=1800
বা, ∠ABC+∠ABC+800=1800
বা, 2∠ABC=1800-800
বা, 2∠ABC=100
বা, ∠ABC = 1000/2
∴ ∠ABC=500
∴ ∠ABC=∠ACB=500
6. AB=AC হলে ∠ACB ও ∠BAC এর পরিমাপ লিখি ।
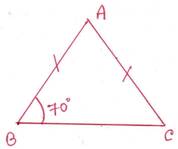
সমাধানঃ ∠ABC=700
∆ ABC এর AB=AC ∴ ∠ABC=∠ACB =700
∆ ABC থেকে পাই,
∠ABC+∠ACB+∠BAC =1800
বা, 700+700 +∠BAC =1800
বা, ∠BAC =1800-700-700
∴ ∠BAC =400
∴ ∠ACB =700 এবং ∠BAC =400
Ganit Prabha Class 8 Koshe Dekhi 16.1|ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি ১৬.১
7. AB=BC এবং ∠BAC + ∠ACB =500 ; ∆ABC এর কোণগুলির পরিমাপ লিখি ।
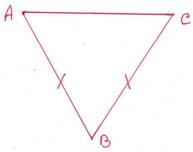
সমাধানঃ ∆ ABC এর AB=BC ∴ ∠BAC=∠ACB
∠BAC+∠ACB=500 [প্রদত্ত]
বা, ∠BAC+∠BAC=500
বা, 2∠BAC =500
∴ ∠BAC =250
∴ ∠BAC =∠ACB =250
∆ABC থেকে পাই,
∠ABC+∠ACB+∠BAC =1800
বা, ∠ABC +500 =1800 [∵∠BAC+∠ACB=500]
বা, ∠ABC =1800-500
∴ ∠ABC =1300
সুতরাং, ∠BAC =∠ACB =250 এবং ∠ABC =1300
8. ∆ABC এর অন্তঃস্থ একটি বিন্দু O; প্রমাণ করি যে ∠BOC>∠BAC
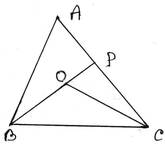
প্রদত্তঃ ∆ABC এর অন্তঃস্থ একটি বিন্দু O
প্রামাণ্যঃ ∠BOC>∠BAC
অঙ্কনঃ BO কে বর্ধিত করা হল যা AC বাহুকে P বিন্দুতে ছেদ করেছে ।
প্রমাণঃ ∆POC এর বহিঃস্থ কোণ ∠BOC =∠OPC+∠OCP
∴ ∠BOC>∠OPC —-(i)
আবার, ∆ ABP এর বহিঃস্থ কোণ ∠BPC =∠ABP+∠BAP
∴ ∠BPC>∠BAP
বা, ∠OPC>∠BAC —-(ii)
(i)নং ও (ii) নং থেকে পাই,
∠BOC>∠BAC [প্রমাণিত]
Ganit Prabha Class 8 Koshe Dekhi 16.1|ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি ১৬.১
9. প্রমাণ করি যে, ∆ABC এর BC বাহুকে উভয়দিকে বাড়ালে যে দুটি বহিঃকোণ উৎপন্ন হয় তাদের সমষ্টি 2 সমকোণের বেশি ।
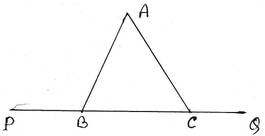
∆ABC এর BC বাহুকে উভয়দিকে বাড়ানোর ফলে দুটি বহিঃকোণ ∠ABP এবং ∠ACQ উৎপন্ন হল ।
প্রামাণ্যঃ ∠ABP +∠ACQ >1800
প্রমাণঃ ∆ABC এর বহিস্থঃকোণ ∠ABP =∠ACB+∠BAC —– (1)
∆ABC এর বহিস্থঃকোণ ∠ACQ =∠ABC+∠BAC —— (2)
(1)+(2) করে পাই,
∠ABP+∠ACQ=∠ACB+∠BAC+∠ABC +∠BAC
বা,∠ABP+∠ACQ=1800+∠BAC [∵ ত্রিভুজের তিনটি কোণের সমষ্টি 1800 , ∴ ∠ACB+∠BAC+∠ABC =1800 ]
∴ ∠ABP+∠ACQ>1800 [প্রমাণিত]
10. ∆ABC এর কৌণিক বিন্দু A ও C দিয়ে যথাক্রমে BC ও BA বাহুর সমান্তরাল সরলরেখাংশ D বিন্দুতে মিলিত হয় । প্রমাণ করি যে, ∠ABC=∠ADC
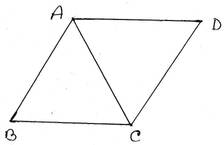
প্রদত্তঃ ∆ABC এর কৌণিক বিন্দু A ও C দিয়ে যথাক্রমে BC ও BA বাহুর সমান্তরাল সরলরেখাংশ D বিন্দুতে মিলিত হয় । অর্থাৎ, AD||BC এবং CD||BA
প্রামাণ্যঃ ∠ABC=∠ADC
প্রমাণঃ ∆ABC থেকে পাই,
∠ABC+∠ACB+∠BAC =1800 —- (1)
∆ ADC থেকে পাই,
∠ADC+∠ACD+∠CAD =1800 ——-(2)
AD||BC এবং AC ছেদক
∴ ∠BCA=∠CAD[একান্তর কোণ]—–(3)
DC||BA এবং AC ছেদক
∴ ∠BAC=∠ACD[একান্তর কোণ]—– (4)
(3) নং ও (4) নং যোগ করে পাই,
∠BCA+∠BAC=∠ACD+∠CAD
বা, 1800-∠ABC=1800-∠ADC [(1) নং ও (2) নং থেকে পাই]
∴ ∠ABC=∠ACD [প্রমাণিত]
Ganit Prabha Class 8 Koshe Dekhi 16.1|ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি ১৬.১
11. ∆ABC এর ∠ABC ও ∠ACB এর অন্তঃসমদ্বিখণ্ডকদ্বয় O বিন্দুতে মিলিত হয় । প্রমাণ করি যে, ∠BOC=900+½∠BAC
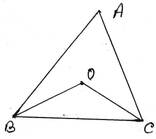
প্রদত্তঃ ∆ABC এর ∠ABC ও ∠ACB এর অন্তঃসমদ্বিখণ্ডকদ্বয় O বিন্দুতে মিলিত হয় ।
প্রামাণ্যঃ ∠BOC=900+½ ∠BAC
প্রমাণঃ ∆ABC এর অন্তঃসমদ্বিখণ্ডক BO
∴ ∠OBC=½∠ABC ——- (1)
∆ACB এর অন্তঃসমদ্বিখণ্ডক CO
∴ ∠OCB=½ ∠ACB —–(2)
∆ABC থেকে পাই,
∠ABC+∠ACB+∠BAC=1800 ——-(3)
∆OBC থেকে পাই,
∠OBC+∠OCB+∠BOC=1800 ——(4)
বা, ½ ∠ABC+½ ∠ACB+∠BOC = 1800
বা, ½ (∠ABC+∠ACB)+∠BOC = 1800
বা, ½ (1800-∠BAC)+∠BOC = 1800
বা, 900-½ ∠BAC+∠BOC = 1800
বা, ∠BOC = 1800-900+ ½ ∠BAC
∴ ∠BOC=900+½ ∠BAC [প্রমাণিত]
12. ∆ABC এর ∠ABC ও ∠ACB বহিঃসমদ্বিখণ্ডকদ্বয় O বিন্দুতে মিলিত হয় । প্রমাণ করি যে, ∠BOC=900– ½ ∠BAC
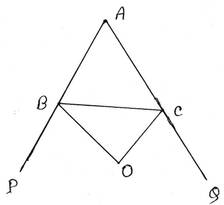
প্রদত্তঃ ∆ABC এর ∠ABC ও ∠ACB বহিঃসমদ্বিখণ্ডকদ্বয় O বিন্দুতে মিলিত হয় ।
প্রামাণ্যঃ ∠BOC=900-½ ∠BAC
প্রমাণঃ ∆ABC থেকে পাই,
∠ABC+∠BCA+∠BAC=1800——(1)
∠ABC এর বহিঃসমদ্বিখণ্ডক BO
∴ ∠OBC=½ ∠CBP ——-(2)
∠ACB এর বহিঃসমদ্বিখণ্ডক CO
∴ ∠OCB=½∠BCQ ——-(3)
∆ABC এর বহিঃকোণ ∠CBP=∠BAC+∠BCA ——(4)
∆ABC এর বহিঃকোণ ∠BCQ=∠ABC+∠BAC —–(5)
∆OBC থেকে পাই,
∠OBC+∠OCB+∠BOC=1800
বা, ½ ∠CBP+½ ∠BCQ+∠BOC=1800 [(2) নং ও (3) নং থেকে পাই]
বা, ½ (∠CBP+∠BCQ)+∠BOC=1800
বা, ½(∠BAC+∠BCA+∠ABC+∠BAC)+∠BOC=1800 [(4) নং ও (5) নং থেকে পাই]
বা, ½ (1800+∠BAC)+∠BOC=1800 [∵ত্রিভুজের তিনটি কোণের সমষ্টি 1800 ]
বা, 900 +½∠BAC+∠BOC=1800
∴ ∠BOC=900-½ ∠BAC [প্রমাণিত]
Ganit Prabha Class 8 Koshe Dekhi 16.1|ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি ১৬.১
গণিতপ্রভা অষ্টম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
13. ∆ABC এর ∠ACB এর বহিঃসমদ্বিখণ্ডক A বিন্দু দিয়ে BC বাহুর সমান্তরাল সরলরেখাকে D বিন্দুতে ছেদ করে । প্রমান করি যে, ∠ADC=900– ½ ∠ACB

প্রদত্তঃ ∆ABC এর ∠ACB এর বহিঃকোণ ∠ACP , ∠ACP এর সমদ্বিখণ্ডক CD এবং AD||BC
প্রামাণ্যঃ ∠ADC=900-½ ∠ACB
প্রমাণঃ BP সরলরেখার উপর CA লম্ব
∴ ∠ACP+∠ACB=1800
বা, ∠ACP =1800-∠ACB ——(1)
∠ACP এর সমদ্বিখণ্ডক CD ∴ ∠DCP=½ ∠ACP —-(2)
AD||BC এবং CD ছেদক
∴ ∠DCP=একান্তর ∠ADC —–(3)
(1)নং ও (2) নং থেকে পাই,
∠DCP=½ (1800-∠ACB) ——(4)
(3)নং ও (4) নং থেকে পাই,
∠ADC=½ (1800-∠ACB)
∴ ∠ADC=900-½ ∠ACB [প্রমাণিত]
14. প্রমাণ করি যে, একটি ত্রিভুজের শীর্ষকোণের সমদ্বিখণ্ডক এবং শীর্ষকোণ থেকে ভূমির উপর অঙ্কিত লম্বের অন্তর্ভুক্ত কোণ ত্রিভুজের ভুমিস্থ কোণদ্বয়ের অন্তরের অর্ধেক ।
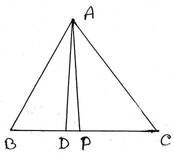
প্রদত্তঃ ∆ABC এর সমদ্বিখণ্ডক AP, BC বাহুকে P বিন্দুতে ছেদ করেছে । A বিন্দু থেকে AD লম্ব যা BC কে D বিন্দুতে ছেদ করেছে । ধরি, ∠ABC>∠ACB
প্রামাণ্যঃ ∠DAP=½(∠ABC -∠ACB)
প্রমাণঃ ∠BAC এর সমদ্বিখণ্ডক AP
∴ ∠CAP= ∠BAP
ABC সমকোণী ত্রিভুজ থেকে পাই,
∠ABD=900-∠BAD—–(1)
ADC সমকোণী ত্রিভুজ থেকে পাই,
∠ACD=900-∠CAD——(2)
(1)-(2) করে পাই,
∠ABD-∠CAD =900-∠BAD-900+∠CAD
বা, ∠ABC-∠ACB=∠CAD-∠BAD
=∠CAP+∠DAP-(∠BAP-∠DAP)
=∠BAP+∠DAP-∠BAP+∠DAP
=2∠DAP
∴ ∠DAP=½(∠ABC -∠ACB) [প্রমাণিত]
Ganit Prabha Class 8 Koshe Dekhi 16.1|ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি ১৬.১
15. ABC সমদ্বিবাহু ত্রিভুজের ভূমির একটি কোণ শীর্ষ কোণের দ্বিগুন । ত্রিভুজটির কোণগুলির পরিমাপ লিখি ।
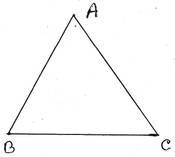
সমাধানঃ ধরি, ∆ABC এর AB = AC
∴ ∠ABC=∠ACB
মনেকরি, ∠BAC=X
∴ ∠ABC=∠ACB=2X
∆ABC থেকে পাই
∠ABC+∠ACB+∠BAC=1800
∴ 2X+2X+X=1800
বা, 5X=180
বা, X= 180 /5
∴ X=36
∴ ∠BAC=360 এবং ∠ABC=∠ACB=2×360=720
16. ∆ABC এর ∠BAC=900 এবং ∠BCA = 300; প্রমান করি যে, AB =½ BC
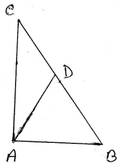
প্রদত্তঃ ∆ABC এর ∠BAC=900 এবং ∠BCA=300
প্রামাণ্যঃ AB= ½ BC
অঙ্কনঃ BC বাহুর উপর AB এর সমান করে BD অংশ কেটে নেওয়া হল । A,D জুক্ত করা হল ।
প্রমাণঃ ∆ABC থেকে পাই,
∠ABC=1800-∠BAC-∠BCA
∴ ∠ABC=1800-900-300=600
∆ABD এর AB=BD [অঙ্কনানুসারে ]
∴ ∠BAD=∠ADB
∆ABD থেকে পাই,
∠ABD+∠ADB+∠BAD=1800
বা, 600+∠BAD+∠BAD=1800 [∵∠BAD=∠ADB]
বা, 2∠BAD=1800-600
বা, ∠BAD= 1200/2 ∴ ∠BAD=600
∴ ∠ABD=∠ADB=∠BAD=600
সুতরাং, ∆ABD একটি সমবাহু ত্রিভুজ
∴ AB=AD=BD —–(i)
∠CAD=900-∠BAD=900-600=300
∆ACD এর ∠CAD=300=∠DCA ∴ AD=CD —-(ii)
(1) নং ও (2) নং থেকে পাই, AD =BD=CD
∴ AD= ½ BC [প্রমাণিত]
Ganit Prabha Class 8 Koshe Dekhi 16.1|ত্রিভুজের কোণ ও বাহুর মধ্যে সম্পর্কের যাচাই কষে দেখি ১৬.১
17. ∆XYZ এর ∠XYZ=900 এবং XY=½ XZ; প্রমাণ করি যে, ∠YXZ=600
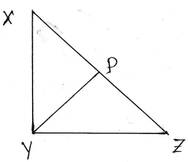
প্রদত্তঃ ∆XYZ এর ∠XYZ=900 এবং XY= ½ XZ
প্রামাণ্যঃ ∠YXZ=600
অঙ্কনঃ Y বিন্দু থেকে ∠Z এর সমান করে ∠PYZ অঙ্কন করলাম ।
প্রমাণঃ ∆PYZ এর ∠PYZ=∠PZY [অঙ্কনানুসারে]
∴ PY =PZ —-(1)
ধরি, ∠PYZ=∠PZY= θ
YXZ সমকোণী ত্রিভুজের ∠YXZ=900-∠XZY
∴ ∠PXY=900-θ
আবার , ∠XYP+∠PYZ=900
বা,∠XYP+θ=900 ∴ ∠XYP=900-θ
∆PXY ত্রিভুজের ∠PXY=∠XYP=900-θ —-(2)
∴ XP=PY —-(3)
(1)নং ও (3) নং থেকে পাই, XP=PZ
∴ PX= ½ XZ
আবার XY=½ XZ ∴ PX= XY
∆XPY এর PX=XY ∴ ∠XPY= ∠XYP —–(4)
(2)নং ও (4) নং থেকে পাই,
∠XPY= ∠XYP=∠PXY
∆XPY এর ∠XPY+∠XYP+∠PXY=1800
বা, ∠PXY+∠PXY+∠PXY=1800
বা, 3∠PXY=1800
∴ ∠PXY=600
∴ ∠YXZ=600 [প্রমাণিত]
18. প্রমাণ করি যে, সমবাহু ত্রিভুজের প্রতিটি কোণের মান 600
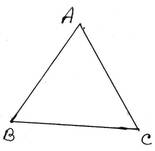
প্রদত্তঃ ABC সমবাহু ত্রিভুজের AB=BC=CA
প্রামাণ্যঃ ∠ABC=∠ACB=∠BAC=600
প্রমাণঃ ∆ABC এর AB=AC
∴ ∠ABC=∠ACB —–(1)
আবার, ∴ ∆ABC এর AB=BC
∴ ∠BAC=∠ACB —–(2)
(1)নং ও (2) নং থেকে পাই,
∠ABC=∠ACB=∠BAC
∆ABC এর ∠ABC+∠ACB+∠BAC=1800
বা, ∠ABC+∠ABC+∠ABC=1800
বা, 3∠ABC=1800
∴ ∠ABC=600
∠ABC=∠ACB=∠BAC=600 [প্রমাণিত]
19. ABC ত্রিভুজের ∠BAC এর সমদ্বিখণ্ডক এবং AC বাহুর মধ্যবিন্দু D দিয়ে AB বাহুর সমান্তরাল সরলরেখা পরস্পর BC বাহুর বাইরে E বিন্দুতে মিলিত হয় । প্রমাণ করি যে, ∠AEC=1 সমকোণ ।
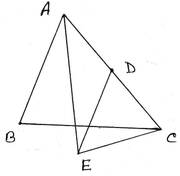
প্রদত্তঃ ABC ত্রিভুজের ∠BAC এর সমদ্বিখণ্ডক এবং AC বাহুর মধ্যবিন্দু D দিয়ে AB বাহুর সমান্তরাল সরলরেখা পরস্পর BC বাহুর বাইরে E বিন্দুতে মিলিত হয় ।
প্রামাণ্যঃ ∠ACE=1 সমকোণ
প্রমাণঃ AB||DE এবং AE ছেদক
∴ ∠BAE=∠AED
∠BAC এর সমদ্বিখণ্ডক AE
∴ ∠BAE=∠EAC
∴ ∠AED=∠EAC=∠EAD [∵∠BAE=∠AED] —–(1)
∆ADE এর ∠AED=∠EAD ∴ AD=DE —- (2)
D, AC বাহুর মধ্যবিন্দু ∴ AD=DC —–(3)
(2)নং ও (3) নং থেকে পাই, DE=DC
∆CDE এর DE=DC ∴ ∠DEC=∠DCE —-(4)
∆ AEC এর ∠AEC+∠ACE+∠EAC= 1800 —–(5)
(1)+(4) করে পাই,
∠AED+∠DEC=∠EAD+∠DCE
বা, ∠AED+∠DEC = ∠EAC+∠ACE
বা, ∠AEC= 1800 -∠AEC [(5) নং থেকে পাই]
বা, 2∠AEC= 1800
∴ ∠AEC=900
∴ ∠ACE=1 সমকোণ [প্রমাণিত]
গণিতপ্রভা অষ্টম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন