Ganit Prabha Class 8 Koshe Dekhi 9|ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক |কষে দেখি ৯ ক্লাস ৮ |WBBSE Class 8 Math Solution Of Chapter 9 Exercise 9|Koshe Dekhi 9 Class Eight| গণিতপ্রভা অষ্টম শ্রেণি (ক্লাস ৮)কষে দেখি ৯ সমাধান ।
গণিতপ্রভা অষ্টম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
Ganit Prabha Class 8 Koshe Dekhi 9|ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক |কষে দেখি ৯ ক্লাস ৮ |WBBSE Class 8 Math Solution Of Chapter 9 Exercise 9|Koshe Dekhi 9 Class Eight| গণিতপ্রভা অষ্টম শ্রেণি (ক্লাস ৮)কষে দেখি ৯সমাধান
কষে দেখি-9
1.নীচের সমদ্বিবাহু ত্রিভুজগুলি দেখি ও না মেপে প্রতিটি ত্রিভুজের কোন দুটি বাহু সমান হবে লিখি:
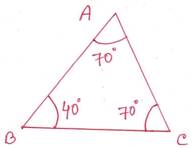
সমাধানঃ প্রথম চিত্রে, ABC ত্রিভুজের ∠BAC=∠ACB= 700
∴ AB=BC
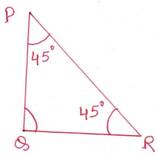
দ্বিতীয় চিত্রে, PQR ত্রিভুজের ∠RPQ=∠PRQ= 450
∴ PQ=QR
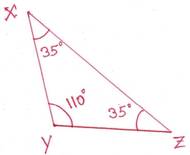
তৃতীয় চিত্রে, XYZ ত্রিভুজের ∠YXZ=∠XZY= 350
∴ XY=YZ
2. নীচের সমদ্বিবাহু ত্রিভুজগুলি দেখি ও না মেপে প্রতিটি ত্রিভুজের কোন কোণগুলি সমান হবে লিখিঃ
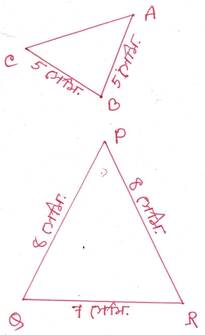
সমাধানঃ প্রথম চিত্রে, ABC ত্রিভুজের AB=BC= 5 সেমি
∴ ∠BCA=∠BAC
দ্বিতীয় চিত্রে, PQR ত্রিভুজের PQ=PR= 8 সেমি
∴ ∠PQR=∠PRQ
3. AB ও CD সরলরেখাংশ দুটি পরস্পরকে O বিন্দুতে সমদ্বিখণ্ডিত করে । প্রমাণ করি যে AC ও BD সরলরেখাংশ দুটি পরস্পর সমান্তরাল । ABCD চতুর্ভুজটি কী ধরনের চতুর্ভুজ তা লিখি ।
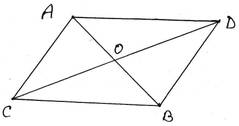
প্রদত্তঃ AB ও CD সরলরেখাংশ দুটি পরস্পরকে O বিন্দুতে সমদ্বিখণ্ডিত করেছে ।
অর্থাৎ AO=OB এবং CO=OD
প্রামাণ্যঃ AC||BD
প্রমাণঃ ∆AOC এবং ∆ BOD এর মধ্যে,
AO=OB [প্রদত্ত]
∠AOC=∠BOD [বিপ্রতীপ কোণ]
CO=OD [প্রদত্ত]
∴ ∆AOC ≅ ∆ BOD [S-A-S সর্বসমতার শর্তানুসারে]
∴ ∠CAO=∠OBD [সর্বসম ত্রিভুজের অনুরূপ কোণ]
∴ ∠CAB=∠ABD
কিন্তু এরা একান্তর কোণ ∴ AB||BD [প্রমাণিত]
একইরকম ভাবে ∆ AOD ও ∆ BOC সর্বসম ত্রিভুজের ক্ষেত্রে প্রমাণ করতে পারি যে,
AD||BC
ABCD চতুর্ভুজের AC||BD এবং AD||BC
∴ ABCD চতুর্ভুজটি একটি সামান্তরিক ।
Ganit Prabha Class 8 Koshe Dekhi 9|ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক |কষে দেখি ৯ ক্লাস ৮
4. AB এবং CD দুটি সমান্তরাল সরলরেখার উপর E ও F দুটি বিন্দু । EF সরলরেখাংশের মধ্যবিন্দু O; O বিন্দু দিয়ে যেকোনো সরলরেখাংশ টানা হল যা AB ও CD সরলরেখাকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে । প্রমাণ করি যে, PQ সরলরেখাংশ O বিন্দুতে সমদ্বিখণ্ডিত হয় ।
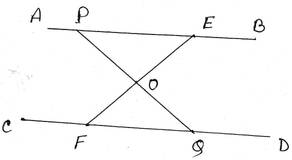
প্রদত্তঃ AB এবং CD দুটি সমান্তরাল সরলরেখার উপর E ও F দুটি বিন্দু । EF সরলরেখাংশের মধ্যবিন্দু O অর্থাৎ, EO=OF , O বিন্দু দিয়ে PQ সরলরেখা টানা হল যা AB ও CD সরলরেখাকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে ।
প্রমাণ্যঃ PO=OQ
প্রমাণঃ ∆ EOP এবং ∆ FOQ এর মধ্যে
∠EOP=∠FOQ [বিপ্রতীপ কোণ]
∠OEP=∠OFQ [∵∠FEP = একান্তর ∠EFQ]
EO=OF [প্রদত্ত]
∴ ∆ EOP ≅ ∆ FOQ [সর্বসমতার A-A-S শর্তানুসারে]
∴ PO=OQ [সর্বসম ত্রিভুজের অনুরূপ বাহু] [প্রমাণিত]
5. প্রমাণ করি যে, একটি সমদ্বিবাহু ত্রিভুজের ভূমিকে উভয়দিকে বর্ধিত করলে যে দুটি বহিঃকোণ উৎপন্ন হয় তাদের পরিমাপ সমান ।
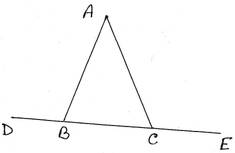
প্রদত্তঃ ধরি, ABC সমদ্বিবাহু ত্রিভুজের AB=AC এবং BC বাহুকে উভয়দিকে বর্ধিত করায় দুটি বহিঃকোণ ∠ABD ও ∠ACE উৎপন্ন হল ।
প্রমাণ্যঃ ∠ABD=∠ACE
প্রমাণঃ ABC সমদ্বিবাহু ত্রিভুজের AB=AC
∴ ∠ABC=∠ACB
DC বাহুর উপর BA দণ্ডায়মান
∴ ∠ABC+∠ABD= 1800 —–(i)
BE বাহুর উপর CA দণ্ডায়মান
∴ ∠ACB+∠ACE= 1800 —–(ii)
(i) নং ও (ii) নং থেকে পাই,
∠ABC+∠ABD=∠ACB+∠ACE
বা, ∠ACB+∠ABD=∠ACB+∠ACE [∵∠ABC=∠ACB]
∴ ∠ABD= ∠ACE [প্রমাণিত]
6. প্রমাণ করি যে, সমবাহু ত্রিভুজের মধ্যমা তিনটির দৈর্ঘ্য সমান ।
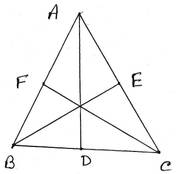
প্রদত্তঃ ABC সমবাহু ত্রিভুজের AD, BE ও CF হল তিনটি মধ্যমা ।
প্রমাণ্যঃ AD=BE=CF
প্রমাণঃ ∆FBC এবং ∆ ECB এর মধ্যে
∠FBC= ∠ECB [∵সমবাহু ত্রিভুজের প্রতিটি কোণ 600]
BF=CE [∵ D, BC বাহুর মধ্যবিন্দু, E, AC বাহুর মধ্যবিন্দু আবার, AB=AC ∴ BF=CE]
BC সাধারণ বাহু
∴ ∆ FBC ≅ ∆ ECB [সর্বসমতার S-S-S শর্তানুসারে]
∴ BE=CF [সর্বসম ত্রিভুজের অনুরূপ বাহু] —-(i)
একইরকম ভাবে ∆ AFC ও ∆ CDA ত্রিভুজদুটি সর্বসম প্রমাণ করে দেখাতে পারি যে,
AD=CF —-(ii)
(i)নং ও (ii) নং থেকে পাই
AD=BE=CF [প্রমাণিত]
Ganit Prabha Class 8 Koshe Dekhi 9|ত্রিভুজের দুটি বাহু ও তাদের বিপরীত কোণের সম্পর্ক |কষে দেখি ৯ ক্লাস ৮
গণিতপ্রভা অষ্টম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন
7. ABCD ট্রাপিজিয়ামের AD||BC এবং ∠ABC= ∠BCD ; প্রমাণ করি যে, ABCD একটি সমদ্বিবাহু ট্রাপিজিয়াম ।
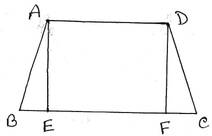
প্রদত্তঃ ABCD ট্রাপিজিয়ামের AD||BC এবং ∠ABC= ∠BCD
প্রমাণ্যঃ ABCD একটি সমদ্বিবাহু ট্রাপিজিয়াম । অর্থাৎ, AB=DC
অঙ্কনঃ A ও D বিন্দু থেকে BC বাহুর উপর যথাক্রমে AE ও DF লম্ব অঙ্কন করলাম ।
প্রমাণঃ ∆ AEB ও ∆ DFC এর মধ্যে
∠ABE= ∠DCF [প্রদত্ত]
∠AEB= ∠DFC [∵AE ও DF, BC বাহুর উপর লম্ব]
AE=DF [∵AD||BC ∴AD ও BC বাহুর মধ্যে লম্ব দুরত্ব সমান]
∴ ∆ AEB ≅ ∆ DFC [সর্বসমতার A-A-S শর্তানুসারে]
∴ AB=DC [সর্বসম ত্রিভুজের অনুরূপ বাহু] [প্রমাণিত]
8. ABC সমকোণী সমদ্বিবাহু ত্রিভুজের AB অতিভুজ । ∠BAC এর সমদ্বিখণ্ডক AD, BC বাহুকে D বিন্দুতে ছেদ করে । প্রমাণ করি যে, AC+CD=AB
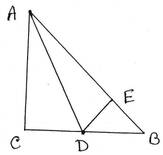
প্রদত্তঃ ABC সমকোণী সমদ্বিবাহু ত্রিভুজের AB অতিভুজ । ∠BAC এর সমদ্বিখণ্ডক AD, BC বাহুকে D বিন্দুতে ছেদ করে ।
প্রমাণ্যঃ AC+CD=AB
অঙ্কনঃ D বিন্দু থেকে AB বাহুর উপর DE লম্ব অঙ্কন করলাম ।
প্রমাণঃ যেহেতু, ABC সমকোণী সমদ্বিবাহু ত্রিভুজের AB অতিভুজ । সুতরাং, ∠ACB=900
∆ACD ও ∆AED এর মধ্যে
∠ACD=∠AED =900 [∵DE ⊥ AB]
∠CAD=∠EAD [∵∠BAC এর সমদ্বিখণ্ডক AD]
AD সাধারণ বাহু
∴ ∆ ACD ≅ ∆ AED [সর্বসমতার A-A-S শর্তানুসারে]
∴ AC=AE এবং CD=DE —-(i)
ABC একটি সমকোণী সমদ্বিবাহু ত্রিভুজ ∴ AC=BC
সুতরাং, ∠CAB =∠ABC=900/2=450
∴ BDE সমকোণী ত্রিভুজের ∠EBD=450 [∵∠ABC=450]
∠EBD=900-450=450
∴ BDE সমকোণী সমদ্বিবাহু ত্রিভুজ
যার ∠EBD=∠EDB ∴ DE=EB —- (ii)
(i)ও (ii) থেকে পাই DE=EB —–(iii)
AC+CD=AE+DE [(i)নং থেকে পাই]
=AE+EB [(iii)নং থেকে পাই]
= AB
∴ AC+CD=AB [প্রমাণিত]
9. ABC এবং DBC দুটি সমদ্বিবাহু ত্রিভুজ যাদের AB=AC ও DB=DC এবং তারা BC বাহুর বিপরীত পাশে অবস্থিত । প্রমাণ করি যে, AD, BC বাহুকে সমকোণে সমদ্বিখণ্ডিত করে ।
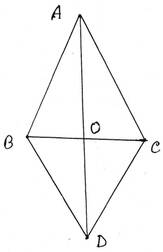
প্রদত্তঃ ABC এবং DBC দুটি সমদ্বিবাহু ত্রিভুজ যাদের AB=AC ও DB=DC ।
ধরি, AD, BC কে O বিন্দুতে ছেদ করেছে ।
প্রামাণ্যঃ AD ,BC বাহুকে সমকোণে সমদ্বিখন্ডিত করে । অর্থাৎ BO =OD এবং AD⊥ BC
প্রমাণঃ ∆ABD ও ∆ ACD এর মধ্যে
AB=AC [প্রদত্ত]
BD=DC [প্রদত্ত]
AD সাধারণ বাহু
∴ ∆ABD ≅ ∆ ACD [সর্বসমতার S-S-S শর্তানুসারে]
∴ ∠BAD=∠CAD [সর্বসম ত্রিভুজের অনুরূপ কোণ]
∴ ∆ ABO ও ∆ ACO এর মধ্যে
AB=AC [প্রদত্ত]
∠BAO= ∠CAO [∵∠BAD=∠CAD]
AO সাধারণ বাহু
∴ ∆ ABO ≅ ∆ ACO [সর্বসমতার S-A-S শর্তানুসারে]
∴ BO=OC [সর্বসম ত্রিভুজের অনুরূপ বাহু]
এবং ∠AOB= ∠AOC [সর্বসম ত্রিভুজের অনুরূপ কোণ]
আবার, BC বাহুর উপর OA দণ্ডায়মান
∴ ∠AOB+∠AOC=1800
বা, ∠AOB+∠AOB=1800
বা, 2∠AOB=1800
∴ ∠AOB=900
∴ AD⊥ BC
সুতরাং, BO=OC এবং AD ⊥ BC [প্রমাণিত]
10. দুটি সরলরেখাংশ PQ ও RS পরস্পরকে X বিন্দুতে এমনভাবে ছেদ করে যাতে XP=XR এবং ∠PSX=∠RQX হয় । প্রমাণ করি যে, ∆ PXS ≅ ∆ RQX
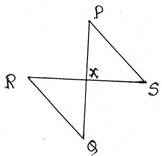
প্রদত্তঃ PQ ও RS সরলরেখা দুটি পরস্পরকে X বিন্দুতে ছেদ করে এবং XP=XR এবং ∠PSX=∠RQX
প্রামাণ্যঃ ∆ PXS ≅ ∆ RQX
প্রমাণঃ ∆ PXS ও ∆ RQX এর মধ্যে
∠PSX=∠RQX [প্রদত্ত]
∠PXS=∠RXQ [বিপ্রতীপ কোণ]
XP=XR [প্রদত্ত]
∴ ∆ PXS ≅ ∆ RQX [সর্বসমতার A-A-S শর্তানুসারে] [প্রমাণিত]
গণিতপ্রভা অষ্টম শ্রেণি বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন