WBBSE Class 9 Math Koshe Dekhi 4| স্থানাঙ্ক জ্যামিতি দূরত্ব নির্ণয় কষে দেখি ৪। গণিত প্রকাশ ক্লাস ৯ কষে দেখি ৪। গণিত প্রকাশ নবম শ্রেণি কষে দেখি ৪। Gonit Prokash Class 9 Koshe Dekhi 4.Class IX Koshe Dekhi 4.গণিত প্রকাশ ক্লাস ৯ স্থানাঙ্ক জ্যামিতি দূরত্ব নির্ণয় কষে দেখি ৪
গণিত প্রকাশ নবম শ্রেণির সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।
মাধ্যমিক গণিত প্রকাশ বইয়ের সকল অধ্যায়ের সমাধানের জন্য এখানে CLICK করুন।
WBBSE Class 9 Math Koshe Dekhi 4|গণিত প্রকাশ ক্লাস ৯ স্থানাঙ্ক জ্যামিতি দূরত্ব নির্ণয় কষে দেখি ৪| গণিত প্রকাশ নবম শ্রেণি কষে দেখি ৪| Gonit Prokash Class 9 Koshe Dekhi 4|Class IX Koshe Dekhi 4
1. মূলবিন্দু থেকে নীচের বিন্দুগুলির দূরত্ব নির্ণয় করিঃ
(i) (7,-24) (ii) (3,-4) (iii) (a+b ,a-b)
সমাধানঃ
(i) মূলবিন্দু (0,0) থেকে (7,-24) এর দূরত্ব

= (5✕5) একক
= 25 একক (উত্তর)
(ii) মূলবিন্দু (0,0) থেকে (3,-4) বিন্দুর দূরত্ব

= √25 একক
= 5 একক (উত্তর)
(iii) মূলবিন্দু (0,0) থেকে (a+b,a-b) বিন্দুর দূরত্ব

2. নীচের বিন্দুযুগলগুলির মধ্যে দূরত্ব নির্ণয় করিঃ
(i) (5,7) এবং (8,3)
সমাধানঃ (5,7) এবং (8,3) বিন্দুদ্বয়ের মধ্যে দূরত্ব

= √25 একক
= 5 একক
(ii) (7,0) এবং (2,-12)
সমাধানঃ (7,0) এবং (2,-12) বিন্দুগুলির মধ্যে দূরত্ব

= √169 একক
= 13 একক
(iii) (-3/2 ,0) এবং ( 0 ,-2)
সমাধানঃ (-3/2 ,0) এবং ( 0 ,-2) বিন্দুদ্বয়ের মধ্যে দূরত্ব

= 2.5 একক
(iv) (3,6) এবং (-2,-6)
সমাধানঃ (3,6) এবং (-2,-6) বিন্দুদ্বয়ের মধ্যে দূরত্ব

= √169 একক
= 13 একক
(v) (1,-3) এবং (8,3)
সমাধানঃ (1,-3) এবং (8,3) বিন্দুগুলির মধ্যে দূরত্ব

= √85 একক
(vi) (5,7) এবং (8,3)
সমাধানঃ (5,7) এবং (8,3) বিন্দুদ্বয়ের মধ্যে দূরত্ব

= √25 একক
= 5 একক
3. প্রমাণ করি যে , (-2,-11) বিন্দুটি (-3,7) ও (4,6) বিন্দুদ্বয় থেকে সমদূরবর্তী ।
সমাধানঃ (-2 ,-11) এবং (-3,7) বিন্দুদ্বয়ের মধ্যে দূরত্ব

∴ (-2,-11) বিন্দুটি (-3,7) ও (4,6) বিন্দুদ্বয় থেকে সমদূরবর্তী ।
4. হিসেব করে দেখাই যে (7,9) ,(3,-7) এবং (-3,3) বিন্দুগুলি একটি সমকোণী ত্রিভুজের শীর্ষবিন্দু ।
সমাধানঃ ধরা যাক , A (7,9) ,B(3,-7) এবং C (-3,3) বিন্দুগুলি একটি ত্রিভুজের শীর্ষবিন্দু ।


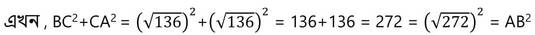
∴ AB2 = BC2+CA2
∴ ABC একটি সমকোণী ত্রিভুজ ।
5. প্রমাণ করি যে ,উভয়ক্ষেত্রে নীচের বিন্দু তিনটি একটি সমদ্বিবাহু ত্রিভুজের শীর্ষবিন্দু ।
(i) (1,4) ,(4,1) ও (8,8)
সমাধানঃ ধরা যাক , A(1,4) , B(4,1) এবং C (8,8) বিন্দু তিনটি ত্রিভুজটির শীর্ষবিন্দু ।

∴ ABC ত্রিভুজের BC ও CA বাহুর দৈর্ঘ্য সমান । অর্থাৎ ABC একটি সমদ্বিবাহু ত্রিভুজ । সুতরাং (1,4) ,(4,1) ও (8,8) বিন্দুগুলি একটি সমদ্বিবাহু ত্রিভুজের শীর্ষবিন্দু ।
(ii) (-2,-2) ,(2,2) ও (4,-4)
সমাধানঃ ধরা যাক , A(-2,-2) , B(2,2) এবং C (4,-4) বিন্দু তিনটি ত্রিভুজটির শীর্ষবিন্দু


∴ ABC ত্রিভুজের BC ও CA বাহুর দৈর্ঘ্য সমান । অর্থাৎ ABC একটি সমদ্বিবাহু ত্রিভুজ । সুতরাং (-2,-2) ,(2,2) ও (4,-4) বিন্দুগুলি একটি সমদ্বিবাহু ত্রিভুজের শীর্ষবিন্দু ।
6. প্রমাণ করি যে , A(3,3) ,B (8,-2) ও C (-2,-2) বিন্দু তিনটি একটি সমকোণী সমদ্বিবাহু ত্রিভুজের শীর্ষবিন্দু । ABC এর অতিভুজের দৈর্ঘ্য নির্ণয় কর ।
সমাধানঃ ABC ত্রিভুজের AB বাহুর দৈর্ঘ্য

এখন , AB2+AC2
= (√50)2+(√50)2
= 50+50
=100
= (10)2
= BC2
∴ AB2 +AC2 =BC2
∴ ABC একটি সমকোণী ত্রিভুজ ।
আবার ABC সমকোণী ত্রিভুজের AB =AC
∴ ABC একটি সমকোণী সমদ্বিবাহু ত্রিভুজ । (প্রমাণিত )
অতিভুজ BC –এর দৈর্ঘ্য 10 একক ।
7. হিসেব করে দেখাই যে , (2,1) ,(0,0) ,(-1,2) এবং (1,3) বিন্দু চারটি একটি বর্গক্ষেত্রের চারটি কৌণিক বিন্দু ।
সমাধানঃ ধরা যাক , A (2,1) ,B (0,0) ,C(-1,2) এবং D (1,3) হল একটি চতুর্ভুজের চারটি কৌণিক বিন্দু । প্রমাণ করতে হবে চতুর্ভুজটি একটি বর্গক্ষেত্র ।


∴ ABCD চতুর্ভুজের AB =BC =CD =DA এবং কর্ণ AC = কর্ণ BD । সুতরাং চতুর্ভুজ ABCD একটি বর্গক্ষেত্র । ( প্রমাণিত )
WBBSE Class 9 Math Koshe Dekhi 4|গণিত প্রকাশ ক্লাস ৯ স্থানাঙ্ক জ্যামিতি দূরত্ব নির্ণয় কষে দেখি ৪| গণিত প্রকাশ নবম শ্রেণি কষে দেখি ৪| Gonit Prokash Class 9 Koshe Dekhi 4
8. হিসেব করে দেখি , y এর মান কী হলে (2,y) এবং (10,-9) বিন্দুদ্বয়ের দূরত্ব 10 একক হবে ।
সমাধানঃ (2,y) এবং (10,-9) বিন্দুদ্বয়ের দূরত্ব 10 একক ।
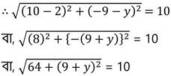
উভয়পক্ষে বর্গ করে পাই ,
64 + (9+y)2 = 100
বা, 64 +81+18y +y2 = 100
বা, y2 + 18y + 145-100=0
বা, y2 +18y + 45 = 0
বা, y2 + (15+3)y + 45=0
বা, y2 +15y +3y +45 = 0
বা, y(y+15) +3(y+15) = 0
বা, (y+15) (y+3) = 0
দুটি রাশির গুনফল শূন্য
∴ হয় , (y+15) = 0
বা, y = -15
অথবা , (y+3) = 0
বা, y = -3
∴ y এর মান -15 বা -3 হলে (2,y) এবং (10,-9) বিন্দুদ্বয়ের দূরত্ব 10 একক হবে ।
WBBSE Class 9 Math Koshe Dekhi 4|গণিত প্রকাশ ক্লাস ৯ স্থানাঙ্ক জ্যামিতি দূরত্ব নির্ণয় কষে দেখি ৪| গণিত প্রকাশ নবম শ্রেণি কষে দেখি ৪| Gonit Prokash Class 9 Koshe Dekhi 4
9. x অক্ষের উপর এমন একটি বিন্দু খুঁজি যা (3,5) ও (1,3) বিন্দুগুলি থেকে সমদূরবর্তী ।
সমাধানঃ ধরি , x অক্ষের উপর বিন্দুটির স্থানাঙ্ক (a,0) ।
শর্তানুসারে ,
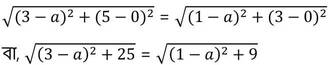
উভয়পক্ষে বর্গ করে পাই ,
(3-a) 2 +25 = (1-a)2+9
বা, 9-6a+a2 +25 = 1-2a +a2+9
বা, a2-a2-6a+2a+9 -9+25-1 = 0
বা, -4a = -24
বা, a = 6
∴ নির্ণেয় বিন্দুটি হল (6,0) যা (3,5) ও (1,3) বিন্দুগুলি থেকে সমদূরবর্তী ।
WBBSE Class 9 Math Koshe Dekhi 4|গণিত প্রকাশ ক্লাস ৯ স্থানাঙ্ক জ্যামিতি দূরত্ব নির্ণয় কষে দেখি ৪| গণিত প্রকাশ নবম শ্রেণি কষে দেখি ৪| Gonit Prokash Class 9 Koshe Dekhi 4
10. O (0,0) ,A(4,3) এবং B (8,6) বিন্দু তিনটি সমরেখ কিনা হিসাব করে লিখি ।
সমাধানঃ O (0,0) ,A(4,3) এবং B (8,6) বিন্দু তিনটি সমরেখ হবে যদি OA +AB = OB হয় ।

∴ OA+AB = (5+5) একক = 10 একক = OB
∴ OA +AB =OB
সুতরাং O(0,0) ,A(4,3) ,B(8,6) বিন্দুত্রয় সমরেখ ।
WBBSE Class 9 Math Koshe Dekhi 4|গণিত প্রকাশ ক্লাস ৯ স্থানাঙ্ক জ্যামিতি দূরত্ব নির্ণয় কষে দেখি ৪| গণিত প্রকাশ নবম শ্রেণি কষে দেখি ৪| Gonit Prokash Class 9 Koshe Dekhi 4
11. দেখাই যে , (2,2) ,(-2,-2) এবং (-2√3 ,2√3) বিন্দু তিনটি একটি সমবাহু ত্রিভুজের শীর্ষবিন্দু ।
সমাধানঃ ধরা যাক , A(2,2) , B(-2,-2) এবং C (-2√3 ,2√3) বিন্দুগুলি একটি ত্রিভুজের শীর্ষবিন্দু ।
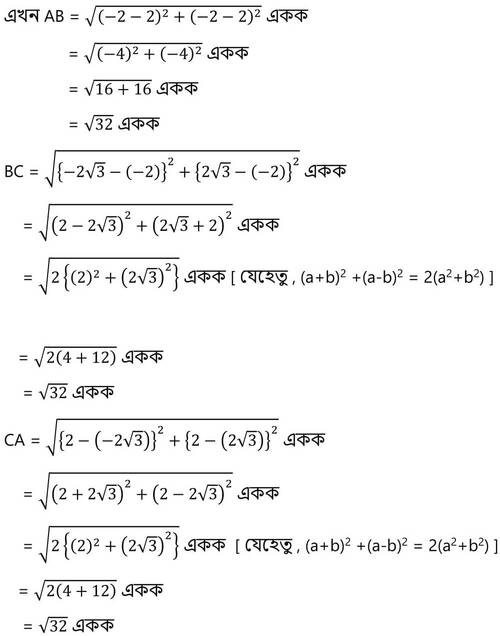
∴ ABC ত্রিভুজের AB = BC =CA
∴ ABC একটি সমবাহু ত্রিভুজ ।
WBBSE Class 9 Math Koshe Dekhi 4|গণিত প্রকাশ ক্লাস ৯ স্থানাঙ্ক জ্যামিতি দূরত্ব নির্ণয় কষে দেখি ৪| গণিত প্রকাশ নবম শ্রেণি কষে দেখি ৪| Gonit Prokash Class 9 Koshe Dekhi 4
12. দেখাই যে , (-7,12) , (19 ,18) , (15,-6) এবং (-11,-12) বিন্দুগুলি পরপর যোগ করলে একটি সামান্তরিক উৎপন্ন হয় ।
সমাধানঃ ধরা যাক , A (-7,12) ,B (19,18) ,C(15,-6) এবং D(-11,-12) হল একটি চতুর্ভুজের চারটি কৌণিক বিন্দু । প্রমাণ করতে হবে চতুর্ভুজটি একটি সামান্তরিক ।


∴ ABCD চতুর্ভুজের AB = CD এবং BC = DA । অর্থাৎ ABCD চতুর্ভুজের বিপরীত বাহুগুলি পরস্পর সমান । সুতরাং চতুর্ভুজটি একটি সামন্তরিক । ( প্রমাণিত )
WBBSE Class 9 Math Koshe Dekhi 4|গণিত প্রকাশ ক্লাস ৯ স্থানাঙ্ক জ্যামিতি দূরত্ব নির্ণয় কষে দেখি ৪| গণিত প্রকাশ নবম শ্রেণি কষে দেখি ৪| Gonit Prokash Class 9 Koshe Dekhi 4
13. দেখাই যে , (2,-2) ,(8,4) ,(5,7) এবং (-1,1) বিন্দুগুলি আয়তক্ষেত্রের শীর্ষবিন্দু ।
সমাধানঃ ধরা যাক , A (2,-2) ) ,B (8,4) ,C(5,7) এবং D(-1,1) হল একটি চতুর্ভুজের চারটি কৌণিক বিন্দু । প্রমাণ করতে হবে চতুর্ভুজটি একটি আয়তক্ষেত্র ।



∴ ABCD চতুর্ভুজের AB = CD , BC = DA এবং কর্ণ AC = কর্ণ BD । অর্থাৎ ABCD চতুর্ভুজের বিপরীত বাহুগুলি পরস্পর সমান এবং কর্ণ দ্বয়ের দৈর্ঘ্য সমান । সুতরাং চতুর্ভুজটি একটি আয়তক্ষেত্র । ( প্রমাণিত )
WBBSE Class 9 Math Koshe Dekhi 4|গণিত প্রকাশ ক্লাস ৯ স্থানাঙ্ক জ্যামিতি দূরত্ব নির্ণয় কষে দেখি ৪| গণিত প্রকাশ নবম শ্রেণি কষে দেখি ৪| Gonit Prokash Class 9 Koshe Dekhi 4
14. দেখাই যে , (2,5) ,(5,9) ,(9,12) এবং (6,8) বিন্দুগুলি পরস্পর যোগ করলে একটি রম্বস উৎপন্ন হয় ।
সমাধানঃ ধরা যাক , A (2,5) ) ,B (5,9) ,C(9,12) এবং D(6,8) হল একটি চতুর্ভুজের চারটি কৌণিক বিন্দু । প্রমাণ করতে হবে চতুর্ভুজটি একটি আয়তক্ষেত্র ।

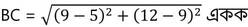

∴ ABCD চতুর্ভুজের AB =BC =CD= DA । সুতরাং চতুর্ভুজটি একটি রম্বস । ( প্রমাণিত )
WBBSE Class 9 Math Koshe Dekhi 4|গণিত প্রকাশ ক্লাস ৯ স্থানাঙ্ক জ্যামিতি দূরত্ব নির্ণয় কষে দেখি ৪| গণিত প্রকাশ নবম শ্রেণি কষে দেখি ৪| Gonit Prokash Class 9 Koshe Dekhi 4
15. বহু বিকল্পীয় প্রশ্ন (M.C.Q):
(i) (a+b,c-d) এবং (a-b , c+d ) বিন্দু দুটির মধ্যে দূরত্ব
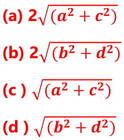
উত্তরঃ 2√(b2+d2)
সমাধানঃ (a+b,c-d) এবং (a-b , c+d ) বিন্দু দুটির মধ্যে দূরত্ব
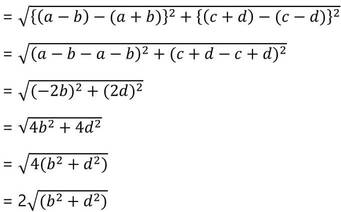
(ii) (x,-7) এবং (3,-3) বিন্দুদ্বয়ের মধ্যে দূরত্ব 5 একক হলে , x –এর মানগুলি হল –
(a) 0 অথবা 6
(b) 2 অথবা 3
(c ) 5 অথবা 1
(d) 6 অথবা 0
উত্তরঃ(a) 0 অথবা 6
সমাধানঃ (x,-7) এবং (3,-3) বিন্দুদ্বয়ের মধ্যে দূরত্ব 5 একক ।
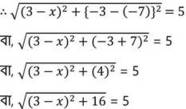
উভয়পক্ষে বর্গ করে পাই ,
(3-x)2 + 16 = 25
বা, (3-x)2 = 25-16
বা, (3-x)2 = 9
বা, 3-x = ±√9
বা, 3-x = ±3
∴ 3-x = 3
বা, x = 0
অথবা , 3-x = – 3
বা, x = 6
∴ x = 0 অথবা x = 6
WBBSE Class 9 Math Koshe Dekhi 4|গণিত প্রকাশ ক্লাস ৯ স্থানাঙ্ক জ্যামিতি দূরত্ব নির্ণয় কষে দেখি ৪| গণিত প্রকাশ নবম শ্রেণি কষে দেখি ৪| Gonit Prokash Class 9 Koshe Dekhi 4
(iii) যদি (x,4) বিন্দুটির মূলবিন্দু থেকে দূরত্ব 5 একক হয় , তাহলে x এর মান
(a) ± 4
(b) ± 5
(c ) ± 3
(d) কোনোটিই নয়
উত্তরঃ (c ) ± 3
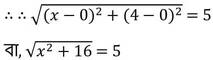
উভয়পক্ষে বর্গ করে পাই ,
x2 +16 = 25
বা, x2 = 25-16
বা, x2 = 9
বা, x = ±√9
বা, x = ±3
(iv) (3,0) ,(-3,0) এবং (0,3) বিন্দু তিনটি যোগ করলে যে ত্রিভুজটি উৎপন্ন হয় সেটি
(a) সমবাহু
(b) সমদ্বিবাহু
(c ) বিষমবাহু
(d) সমকোণী সমদ্বিবাহু
উত্তরঃ (d) সমকোণী সমদ্বিবাহু
সমাধানঃ ধরা যাক , A(3,0) , B(-3,0) এবং C (0,3) বিন্দুগুলি একটি ত্রিভুজের শীর্ষবিন্দু ।

BC2 + CA2 = (√18)2+(√18)2 = 18+18 = 36 = (6)2 = AB2
∴ ABC ত্রিভুজের BC ও CA বাহুর দৈর্ঘ্য পরস্পর সমান এবং BC2+CA2 =AB2
∴ ABC একটি সমকোণী সমদ্বিবাহু ত্রিভুজ ।
(v ) একটি বৃত্তের কেন্দ্রের স্থানাঙ্ক (0,0) এবং বৃত্তের উপরিস্থিত একটি বিন্দুর স্থানাঙ্ক (3,4) হলে , বৃত্তটির ব্যাসার্ধের দৈর্ঘ্য
(a) 5 একক
(b) 4 একক
(c ) 3 একক
(d) কোনোটিই নয়
উত্তরঃ(a) 5 একক
সমাধানঃ বৃত্তের কেন্দ্রের স্থানাঙ্ক (0,0) এবং বৃত্তের উপরিস্থিত একটি বিন্দুর স্থানাঙ্ক (3,4) হলে , বৃত্তটির ব্যাসার্ধের দৈর্ঘ্য

= √25 একক
= 5 একক
16. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ
(i)মূলবিন্দু থেকে (-4,y) বিন্দুর দূরত্ব 5 একক হলে , y এর মান কত লিখি ।
সমাধানঃ মূলবিন্দু (0,0) থেকে (-4,y) বিন্দুর দূরত্ব 5 একক
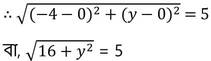
উভয়পক্ষে বর্গ করে পাই ,
16+y2 = 25
বা, y2 = 25-16
বা, y2 = 9
বা, y = ±√9
বা, y = ± 3
∴ y এর মান ± 3 ।
(ii) y –অক্ষের উপর একটি বিন্দুর স্থানাঙ্ক লিখি যার থেকে (2,3) এবং (-1,2) বিন্দু দুটির দূরত্ব সমান ।
সমাধানঃ ধরি , y অক্ষের উপর বিন্দুটি হল (0,a) যার থেকে (2,3) এবং (-1,2) বিন্দু দুটির দূরত্ব সমান ।
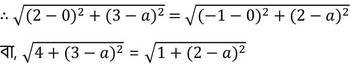
উভয়পক্ষে বর্গ করে পাই ,
4+ (3-a)2 = 1+(2-a)2
বা, 4 + 9 – 6a +a2 = 1+4-4a+a2
বা, 13-6a+a2 = 5-4a+a2
বা, 13-5 = 6a -4a
বা, 8 = 2a
বা, a = 8/2
বা, a = 4
∴ y অক্ষের উপর বিন্দুটির স্থানাঙ্ক হল (0,4) ।
(iii) x-অক্ষ এবং y-অক্ষের উপর দুটি বিন্দুর স্থানাঙ্ক লিখি যাতে x অক্ষ ,y অক্ষ এবং বিন্দু দুটির সংযোগকারী সরলরেখাংশ দ্বারা উৎপন্ন ত্রিভুজটি সমকোণী ত্রিভুজ হয় ।
সমাধানঃ x-অক্ষ এবং y-অক্ষের উপর দুটি বিন্দুর স্থানাঙ্ক হল (6,0 ) এবং (0,6)
এই বিন্দু দুটির সংযোগকারী সরলরেখাংশ দ্বারা উৎপন্ন ত্রিভুজটি সমকোণী ত্রিভুজ হয় ।
(iv) x –অক্ষের বিপরীত দিকে দুটি বিন্দুর স্থানাঙ্ক লিখি যাদের দূরত্ব x অক্ষ থেকে সমান ।
সমাধানঃ x –অক্ষের বিপরীত দিকে দুটি বিন্দুর স্থানাঙ্ক হল – (6,3) এবং (6,-3) যাদের দূরত্ব x অক্ষ থেকে সমান ।
(v) y –অক্ষের বিপরীত দিকে দুটি বিন্দুর স্থানাঙ্ক লিখি যাদের দূরত্ব y অক্ষ থেকে সমান ।
সমাধানঃ y –অক্ষের বিপরীত দিকে দুটি বিন্দুর স্থানাঙ্ক হল (8,6) এবং (-8,6) যাদের দূরত্ব y অক্ষ থেকে সমান ।
16(iii) ,16(iv) এবং 16(v) এই প্রশ্নগুলির অন্য উত্তর হতে পারে ।
Good
12 এর দাগের অংকে, কর্ণ দুটির দৈর্ঘ্যও অসমান দেখাতে হবে কারণ আয়তক্ষেত্রেরও দুই জোড়া বিপরীত বাহু সমান।
একইরকম 14 এর দাগের অংকে কর্ণ দুটির দৈর্ঘ্য অসমান দেখাতে হবে, কারণ বর্গক্ষেত্র ও রম্বস উভয়েরই দুই জোড়া বিপরীত বাহু সমান।
Thank you anushilon.com
Best mathematics 👍
That’s good, 😄
Thanks for this math.
Thank you very much anushilan. com
Thank you very much anushilan.com